公交线路资源配置与客流状况协调性综合评价方法*

马嘉欣 陈旭梅▲ 柯靖宇 彭 飞

（1.北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室 北京100044；2.南京市城市与交通规划设计研究院股份有限公司 南京210008）

0 引 言

近年来，随着我国城镇化建设稳步推进，常规公交发展总体保持迅速增长态势。然而，城镇人口的高度聚集与人民生活水平的提高引发了多层次、多样化的出行需求，进而对公交线网的运输资源配置提出了更高的要求。据《2020—2026年中国城市公交行业现状分析与发展前景预测报告》[1]显示，目前我国城市常规公交仍存在有效供给能力不足、车速较低、准点率较差等问题。公交线路资源配置与客流状况间的协调性短板亟需补齐。因此，客观、合理评估城市常规公交线路运输现状，以线路-网络逐步提升资源配置与客流状况的匹配程度，对提升城市常规公交服务质量至关重要。

目前，国内外学者针对常规公交协调性的研究大多集中在常规公交整体系统与相关社会经济行业间以及其与轨道交通之间，如吴瑶等[2]、玛依拉·艾则孜等[3]分别对常规公交与经济发展间的协调程度进行研究，Erick等[4]、朱丽等[5]、Zhang等[6]探讨常规公交与城市发展之间的协调性及其相互影响关系，谢天[7]、Dou等[8]则研究常规公交与轨道交通间的协调性。然而，城市常规公交系统作为复杂、开放的有机整体包含站点、线路、客流等多类影响因素，现有研究中仍鲜有面向常规公交进行考虑系统内部多因素协调性的分析，仅冯树民等[9]、刘新民等[10]、Pitam等[11]与Hahn等[12]分别研究不同条件下线路资源配置与客流量或服务质量的协调性。

数据包络分析法（data envelopment analysis，DEA）作为1种有效的无量纲相对评价方法，因其处理多投入、多产出问题的优越性[13]而在常规公交协调性研究中被广泛应用，Charnes等[13]提出的锥比率C2WH模型作为DEA的典型方法之一也在强调评估偏好的研究中逐渐推广。但DEA方法在具体应用的过程中存在有效决策单元（Decision Making Unit，DMU）无法细分优劣性[14-15]、影响因素及影响效应确定主观性较强等问题[16]，仍有一定的改进空间。针对有效DMU问题，相关学者提出引入理想点的C2WH（Charnes-Cooper-Wei-Huang Model）[17]等衍生模型丰富DEA评价方法。针对影响因素与影响效应问题，结构方程模型（Structural Equation Modeling，SEM）在检验模型变量对评价对象解释能力的基础上，还可分析各变量对评价对象的直接影响、间接影响和总影响等量化数值[18]，为该问题提供新的解决思路。

综上所述，国内外针对常规公交协调性研究已取得了一定的进展，但聚焦常规公交线路资源配置与客流状况间的协调性研究仍较少，且所应用方法存在多个有效DMU、关键与非关键因素辨识度较差、各因素与二者协调性间的影响关系难以量化等问题。鉴于现有研究的局限性，本文将利用结构方程模型、基于理想点的改进DEA模型综合提出公交线路资源配置与客流状况协调性评价方法，并选取北京市海淀区65条公交线路作为实例以验证所提出方法的有效性。

1 指标体系构建

公交线路资源配置与客流状况的协调性是指在一定的时间段内公交线路可利用的资源与所吸引的最大客流量相匹配的良好状态。二者综合作用、相互制衡，最终体现为线路在现有资源条件下尽可能满足沿线客流需求。

公交线路资源配置往往受到一定的软限制与硬限制，分别对应运营状况与基本布设。根据GB∕T 37114—2018《公共汽电车线网设置和调整规则》（以下简称《规则》），在基本布设一级指标下选取线路长度、平均站点间距、非直线系数这3个二级指标。而由于公交线路布设具有成网特性且部分居民出行起讫点间无直达公交线路，还需考虑线路间的换乘因素，额外添加换乘站点比例这1个二级指标；在运营状况一级指标下选取发车间隔、平均运送速度这2个二级指标，并提出车辆定员二级指标以量化《规则》中“运营车辆选型配置”指标。

公交线路客流状况是线路在运营时所吸引的客流及其特征的相关指标，体现城镇居民对线路的实际需求。根据上述《规则》，选取日客运总量指标，且考虑本文主要从整体时段角度评估线路资源配置与客流状况协调性而非单一时段，提出平均满载率指标替代《规则》中“高峰小时平均满载率”指标。此外，为充分评估沿线客流与线路资源间的协调程度，进一步提出日客运周转量指标。

综上，公交线路资源配置与客流状况协调性指标体系见表1。

表1 指标体系Tab.1 Indicator system

2 综合评价方法

2.1 评价方法思路

根据所构建的公交线路资源配置与客流状况协调性评价指标体系，本文应用IC卡数据扩样方法以丰富原始数据，引入结构方程模型确定有效指标及其相对应的影响效应，并结合基于理想点的改进DEA模型以实现公交线路资源配置与客流状况协调性的综合评价，见图1。

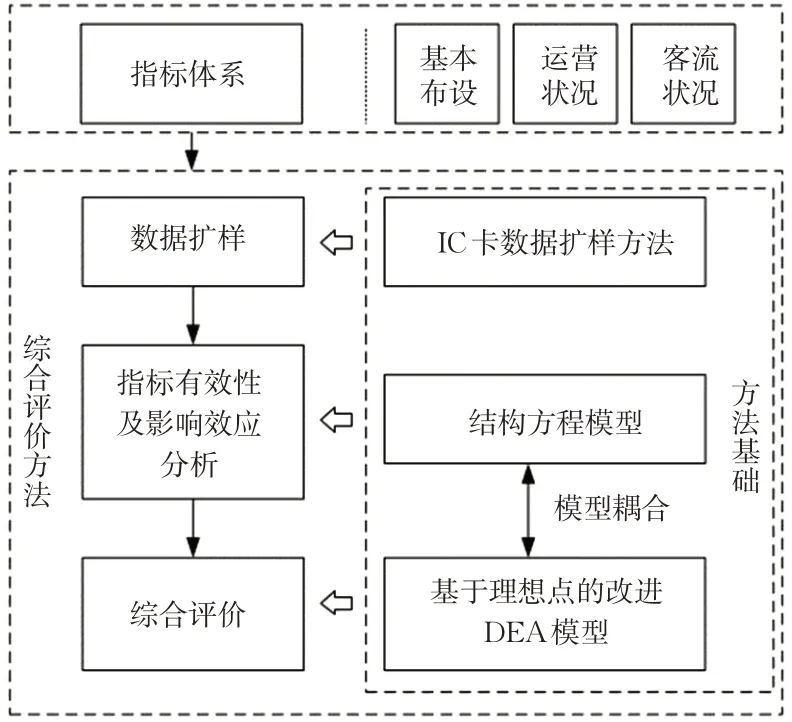
图1 评价方法思路Fig.1 Approach of the evaluation method

2.2 IC卡数据扩样方法

考虑到IC卡数据是现有公交线路协调性评价研究中的主要数据源之一，但该数据尚不能普及全部常规公交出行者，且仍存在原始数据中数据缺失、数据错误等问题，需对公交线路客流数据进行扩样，扩样公式见式（1）～（2）[19]。

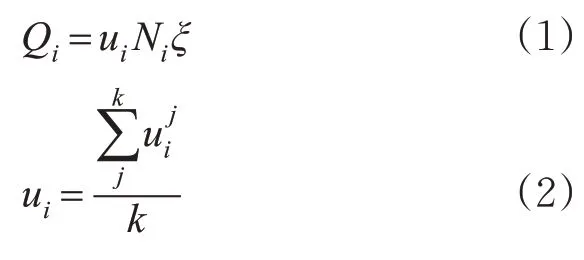
式中：Qi为扩样后线路i的客流数据，人·次；ui为线路i的扩样系数；Ni为线路i的刷卡量，人·次；ξ为日交通不均匀系数；为线路i第j车次的刷卡率；k为调查时段内线路i的车次数。

2.3 结构方程模型

由于DEA模型在具体评价过程中仍存在难以判断有效指标、有效指标间作用关系不明及影响效应确定主观等劣势，故引入结构方程模型。

结构方程模型包含显变量（可直接测量因素）和潜变量（不可直接测量因素）2类变量，可对变量有效性及变量间作用的各种影响效应进行判断分析，是1种综合性较强的统计分析方法。根据变量间关系，结构方程模型可划分为结构模型与测量模型，测量模型还可进一步分为构成型测量模型与反映型测量模型[16]。结构模型、构成型测量模型与反映型测量模型见式（3）～（5）。

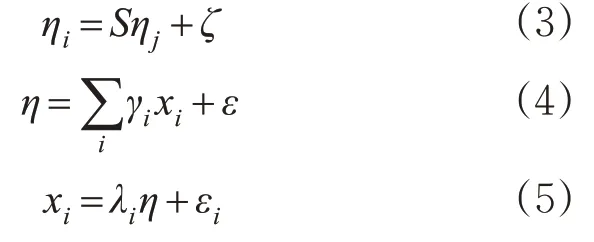
式中：η为潜变量；S为潜变量的路径系数；ζ为残差；γi为第i个显变量对潜变量的解释系数，即权重；xi为第i个显变量；ε为随机误差；λi为潜变量对第i个显变量的解释系数，即载荷；εi为测量误差。

在公交线路资源配置与客流状况协调性综合评价中，基本布设、运营状况与客流状况因无法通过数据测量等手段直接获得而判定为潜变量，线路长度、发车间隔、日客运总量等为显变量。之后，形成由3个潜变量组成的1个结构模型、包含潜变量及其对应显变量的3个测量模型，3个测量模型又细分为分别以基本布设、运营状况为潜变量的2个构成型测量模型和以客流状况为潜变量的1个反映型测量模型。

选用偏最小二乘法（partial least squares，PLS）进行模型内的路径系数估算。设基本布设等潜变量为ηi，线路长度等显变量为xij。具体估算过程为：若潜变量η1与η2相关，则结构模型路径系数为e12=cor(η1，η2)。若潜变量η2估值为q2，则针对潜变量η1的估值为若潜变量η1与显变量x12相关，则测量模型路径系数为r12=cor(x12，z1)[20]。其余变量间路径系数估算同理。

为进一步验证模型对各变量解释的科学性，仍需对所建模型进行相应的效度检验、显著性检验等，并根据检验结果修正模型，筛选有效指标，获得指标重要度排序，进而为公交线路资源配置与客流状况协调性综合评价奠定基础。

2.4 基于理想点的改进DEA模型

为客观、合理评价公交线路资源配置与客流状况协调性，各指标重要度也应在评价过程中有所体现。因此，本文选用DEA方法中可以体现指标权重偏好的锥比率C2WH模型[16]作为基础模型，并将基本布设、运营状况指标对应的二级指标作为投入指标，客流状况指标对应的二级指标作为产出指标。

若每个DMU有n个投入指标与s个产出指标，则可建立相应的投入指标权重向量w=(w1，w2，…，wn)T与产出指标权重向量v=(v1，v2，…，v s)T。其中，w为各投入指标的权重，v为各产出指标的权重。若各投入指标的影响效应排序确定为w=(w1≥w2≥…≥wn)T，即权重偏好确定时，投入指标权重偏好矩阵仅由-1,0,1组成。投入指标权重偏好限制过程见式（6）。产出指标权重偏好矩阵确定过程同理。

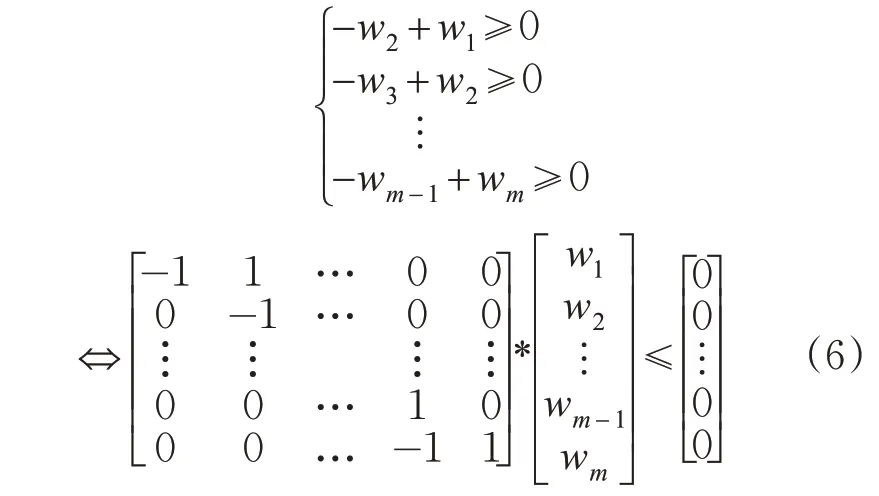
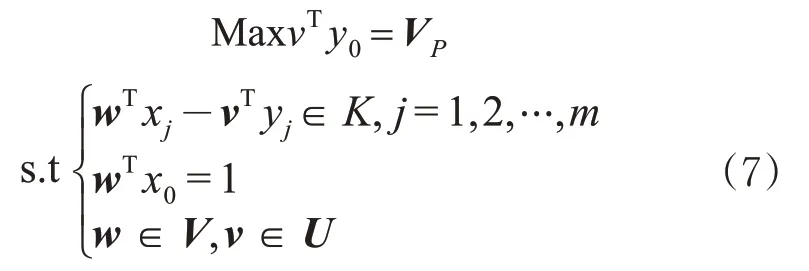
若上述方程存在最优解w0和v0满足v0Ty0=1，w0∈IntV，v0∈IntU，则DMUj0为DEA有效。

为进一步简化模型，V，U，K可取为多面凸锥，见式（8）～（9）。

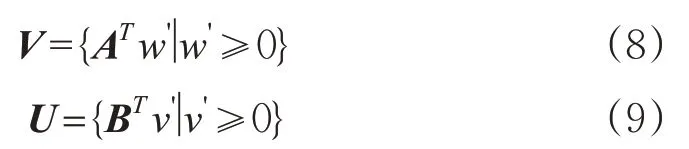
式中：A为m阶方阵，为偏好约束锥的约束矩阵；B为s阶方阵，为偏好约束锥的约束矩阵。

因此，式（7）进一步简化为

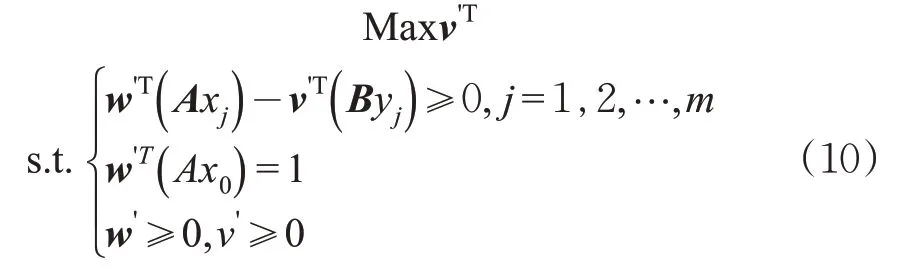
最后，引入理想点解决评价结果中可能出现多个有效DMU的问题[17]。其核心思想为虚拟1个投入最小而产出最大的理想点作为唯一有效DMU，令其他参与实际评价的DMU变为无效，获得相对效率排序，从而进行综合评价。

3 案例分析

3.1 数据来源及扩样

本文选取北京市海淀区65条公交线路，收集上述线路工作日连续3天的IC卡数据，在数据扩样后获得全客流样本，进而计算各指标值进行模型标定及检验，并以海淀区香山地区10条公交线路作为典型对象进行案例分析。

3.2 指标有效性检验及影响效应标定

基于所构建的公交线路资源配置与客流状况协调性结构方程模型，利用SmartPLS3.0软件对模型进行PLS路径系数计算，计算结果见图2。

由图2所示模型各变量关系及其相关参数，可建立对应的测量模型见式（11）～（13），结构模型见式（14）～（15）。

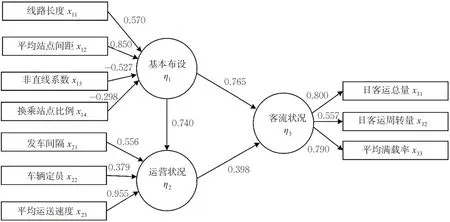
图2 PLS路径模型计算结果Fig.2 Estimation of the PLS-path model

之后，应用SmartPLS3.0软件对模型进行效度检验与显著性检验。效度检验主要针对构成型测量模型进行方差膨胀系数（variance inflation factor，VIF）检验，针对反映型测量模型进行组合信度（composite reliability，CR）、平均方差提取量（average variance extracted，AVE）和克朗巴哈系数（Cronbachs'α）检验，针对结构模型进行方程确定系数（coefficient of determination，R2）检验。显著性检验则针对各显变量及路径系数进行T统计量检验。检验结果分别见表2和表3。

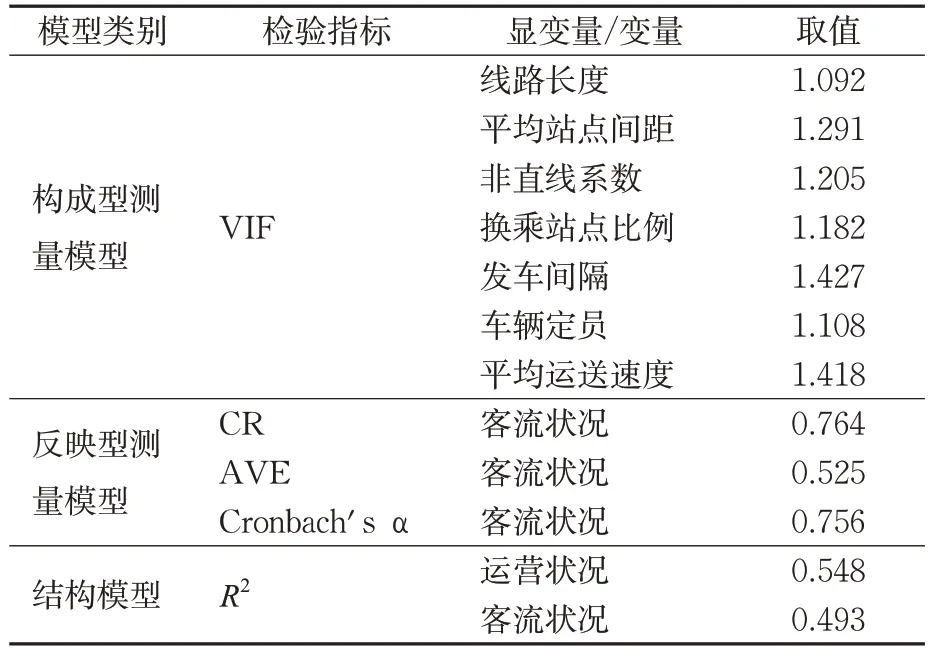
表2 效度检验Tab.2 Validity test of the proposed model

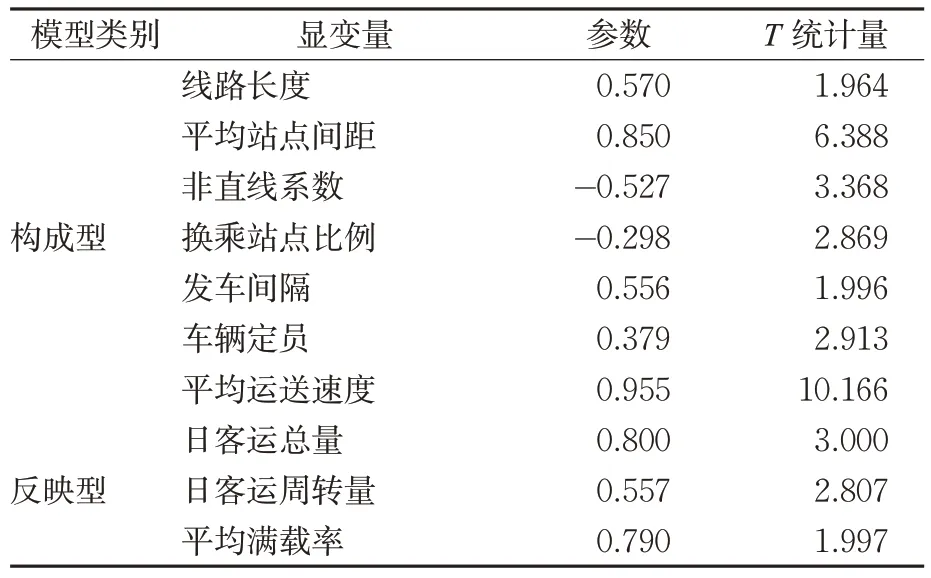
表3 参数显著性检验Tab.3 Significance test of parameters

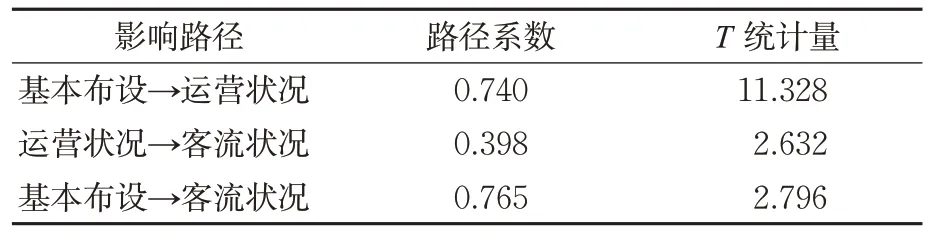
表4 路径系数显著性检验Tab.4 Significance test of path coefficient

见表2，分析变量间的共线性VIF值均小于10，表明构成型测量模型的有效性满足要求。反映型测量模型中CR≥0.7、AVE≥0.5、Cronbach'sα≥0.7，各项检验结果均较好，表明该模型具有较好的收敛有效性与内部一致性。此外，针对结构方程模型而言，R2用来反映基本布设对运营状况、基本布设与运营状况对客流状况的解释能力，认为R2≥0.66时解释能力优秀，0.66＞R2≥0.35时解释能力良好，0.35＞R2≥0.17时解释能力较弱，若R2＜0.17则不可接受解释关系[16，20]。由表2可知，R2取值均大于0.35，表明模型内变量解释能力良好。因此，该模型效度较好，可靠性较高。

见表3～4，模型参数的显著性检验是针对路径载荷/权重、路径系数等的路径参数进行T统计量检验。在显著性水平为0.05的条件下，T统计量均大于1.96，变量间的影响关系有效。其中，相较于运营状况，基本布设对客流状况的影响更为显著，路径系数达0.765。

综上，公交线路资源配置与客流状况协调性结构方程模型通过各项检验，各项评价指标有效，无需进行指标的修正或删减。

为进一步研究各指标对二者协调性的不同影响程度，对其进行影响效应分析。按照2个变量间是否经由中间变量相连，将影响效应划分为直接影响效应和间接影响效应。基于公交线路资源配置与客流状况协调性结构方程模型的路径参数计算结果，汇总各变量的直接影响效应和间接影响效应，获得总影响效应。效应影响取值见表5。

由表5可知，作为投入变量的显变量共7项，按照总效应的取值大小确定影响效应排序，具体是平均站点间距＞线路长度＞非直线系数＞平均运送速度＞换乘站点比例＞发车间隔＞车辆定员；作为产出变量的显变量共3项，影响效应排序为日客运总量＞平均满载率＞日客运周转量。

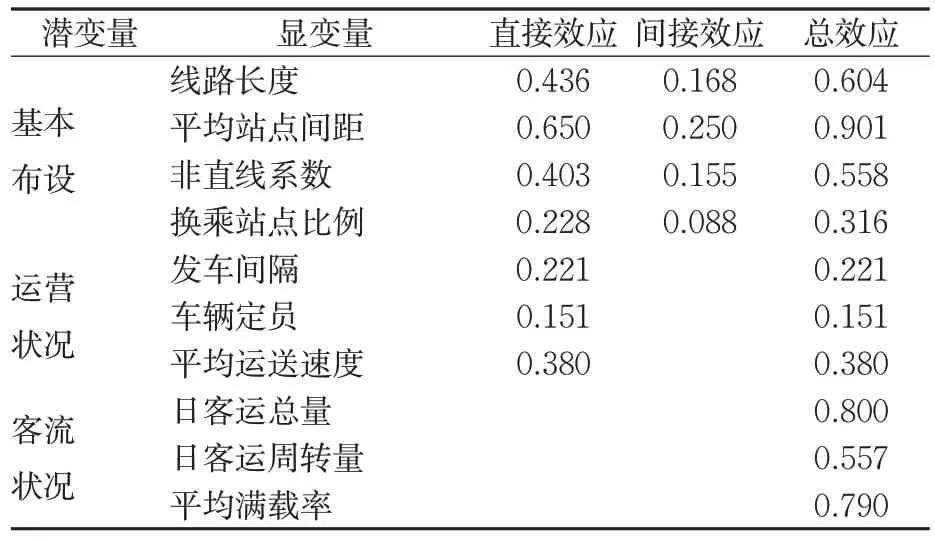
表5 各指标影响效应值Tab.5 Effectiveness of the factors

3.3 综合评价及分析

选取海淀区香山地区10条公交线路进行典型案例评价，该地区公交线路整体资源配置较低，客流具有季节分布不均、短期激增及局部密集等特点，需综合把握各线路资源配置与客流状况协调性，进而提升该地常规公交线网的整体服务水平。

基于各条线路相关数据，确定理想DMU各指标取值，见表6。

表6 理想DMU指标值Tab.6 Indicator values of the ideal DMU

根据公交线路资源配置与客流状况协调性结构方程模型中确定的各指标影响效应排序，构建投入指标偏好矩阵及产出指标偏好矩阵，见式（16）～（17）。

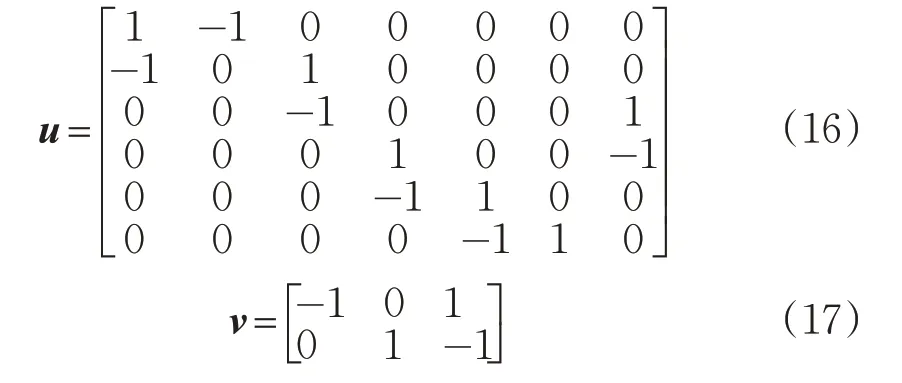
最后，分别运用Matlab软件对本文所提出的方法及传统DEA方法进行求解，获得10条公交线路资源配置与客流状况协调性的效率值及其排序，求解结果见图3。

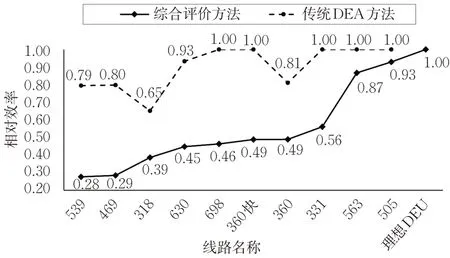
图3 评价结果Fig.3 Evaluation results

见图3，根据传统DEA方法评价结果，563和505等5条线路的相对效率取值均为1，难以针对上述线路进一步评价其资源配置与客流状况协调性优劣。此外，结合实地调研结果，698线路各时段平均满载率较低；360快线路平均站点间距远超同类型线路建议值；331线路途经高校、医院、写字楼等客流发生和吸引点，高峰时段存在多个断面客流峰值，潮汐现象明显，但非直线系数较高、平均运送速度较慢。相较于实际情况，针对上述3条线路的资源配置与客流状况协调性评价结果均存在不同程度的高估问题。

结合本文所提出的综合评价方法进行评价，除理想DMU的效率达到最优外，其他DMU相对效率均分布于（0，1）区间内，且10条公交线路资源配置与客流状况协调性明显划分为3个等级，等级间效率均出现显著跃升，分别为位于（0，0.30]效率区间内的539和469线路，位于[0.30，0.60]效率区间内的318和630等线路，位于[0.60，1.00）效率区间内的563和505线路。

针对539和469线路进行分析，这2条线路均为该地区支线线路，资源配置较低，但由于主要承担颐和园至地铁10号线间的接驳任务而早晚通勤期间客流较大，加之旅游旺季时大量不均衡客流叠加，线路资源配置与客流状况间的协调性相对较差。而563和505线路等为香山地区连接城区的长途线路，日均客流量较大，平均运送速度较快，线路资源配置与客流状况协调性较好。上述评价结果也与线路等级等实际情况相符。

此外，根据指标影响效应排序，建议评价结果较差的公交线路，如539线路、469线路等，从平均站点间距、线路长度等方向依次进行优化以提升公交线路资源配置与客流状况协调性。

4 结束语

科学评估公交线路资源配置与客流状况协调性是针对性优化线网布局及提升服务质量的必然要求。本文结合结构方程模型、基于理想点的改进DEA模型提出公交线路资源配置与客流状况协调性综合评价方法，有效识别关键指标并确定其影响效应，进而获得评价对象的差异化排序，对公交网络整体布局的定向优化具有指导意义，获得的主要结论如下。

1）公交线路资源配置与客流状况协调性受平均站点间距、线路长度、非直线系数、平均运送速度、换乘站点比例等因素的影响效应依次递减。其中，平均站点间距的影响效应达到0.901。

2）针对应用传统DEA方法评价时5条公交线路相对效率均取值为1而难以细分优劣的问题，所提出的公交线路资源配置与客流状况协调性综合评价方法可获得差异化排序，且排序结果符合线路等级及实际运营情况。