基于复杂网络理论的城轨线网抗毁性对比分析*

2021-07-29赵瑞琳牟海波杨景峰

交通信息与安全 2021年3期

赵瑞琳牟海波肖丁杨景峰

（兰州交通大学交通运输学院兰州730070）

0 引言

截至2020年底，仅在中国大陆地区已有45个城市开通城市轨道交通，运营线路244条[1]。发展水平不同的城市对轨道交通的投入程度不同，但发展方向多为由独立单线逐步构建成网络，其目的是利用城市轨道交通的优点使之成为整座城市正常高效运转的重要一环。因此，分析现有不同规模城市轨道交通网络的抗毁性，定量化判断路网何时失效，挖掘网络中的脆弱节点对科学处理突发事件具有重要意义。

现阶段国内外对轨道交通网络的分析已有较多研究成果。许多学者利用站点和线路间关系构造抽象的网络拓扑结构，方便对现实路网进行指标分析[2-3]。许多较发达的交通路网都具有小世界和无标度特性[4-5]。在对城轨线网进行抗毁性分析时，文献多将平均度、平均路径长度、聚类系数、网络效率等作为衡量指标[6-7]。不少学者通过对指标计算方法进行改进、指标范围进行拓展，以期得到更精准、更全面的分析数据[8-10]。

现有研究多以随机攻击和蓄意攻击2种方式对路网进行抗毁性分析[11-13]。吴贤国等[14]系统分析了武汉市的地铁网络在随机攻击、蓄意攻击（细分为单节点蓄意攻击和累计节点蓄意攻击）3种模拟攻击下网络静态与动态脆弱性水平。王彬等[15]构建级联失效模型，以北京市为例对比分析不同节点攻击下地铁网络抗毁性。冯树民等[16]构建了轨道交通网络抗毁性分析模型，提出了1种新的换乘站脆弱性测算方法，以上海市为例对路网进行抗毁性分析。段家勇等[17]设计1种基于节点重要度的复杂网络脆弱性分析方法并以某城区铁路网络为例进行单节点攻击和多节点攻击。邓旭东等[18]构建地铁网络脆弱性评价模型，以北京市地铁网络为例进行随机攻击、最大度节点攻击和最高介数节点攻击来讨论地铁网络的脆弱性。

但以上研究仅将单一城市的轨道线网作为对象进行抗毁性分析，未分析突发事件对不同规模城轨路网的影响程度是否不同；只对网络攻击的结果进行单纯归纳总结，没有对评判标准定量化；也未系统分析突发事件种类和攻击类型之间的对应关系。

笔者利用复杂网络理论，构建中国10个典型城市轨道交通的无向非计权拓扑网络，在静态点线间指标和动态稳定性指标下对网络进行模拟攻击，分析其性质找到路网的脆弱点以及路网失效的临界值，以期将所得结果用于应对现实中城市地铁突发事件的事前预警防御、事中决策处置、事后评估维护，为城市轨道交通高效、安全、系统的运行提供数据支撑。

1 拓扑结构模型构建

网络是指由节点和连线构成的图。复杂网络（complex network）是现实中大量真实复杂系统的高度抽象，它是指具有自组织、自相似、多融合、无标度、小世界中部分或全部性质的网络[12，19]。复杂网络拓扑空间的构建常见方法有Space-L，Space-P，Space-R。其中Space-L方法将站点作为节点，若2个站点相邻并有同1条线路通过，则节点之间有连边，还原现实点线间关系程度高。本文主要研究对象是城市整体轨道交通网络，使用Space-L方法可以更好的体现整体路网特性。

因站点间距离、站点面积不作为本文研究路网抗毁性的对象，所以构造各城市轨道交通非计权拓扑网络。构造步骤见图1。

图1 构造拓扑网络步骤图Fig.1 Steps for constructing a topological network

本文标号准则可归纳如下。

1）通过但不经停的站点不标记（多为暂未开通站点）。

2）分支线不标记（此类分支线既未与其他线路有换乘点，且删除分支线上的节点对整体路网影响极小）。

3）标号线路不包含快线（上海、成都）和有轨电车（广州、杭州、成都）、APM线（广州）。

4）超大型枢纽站多个出站口只定义1个标号（例如上海的南京西路站、北京的首都机场二号航站楼站和三号航站楼站）。

本文构建邻接矩阵方法与文献[20]方法一致，根据构造步骤，以深圳市城市轨道交通线网为例，可得到深圳市现有地铁线路拓扑结构，见图2。

图2 深圳市现阶段地铁线路拓扑结构Fig.2 Topology structure of current Shenzhen metro network

2 网络抗毁性分析指标及攻击方式

2.1 城轨交通网络抗毁性分析指标

在分析Space-L法构建的拓扑空间时，既要对网络本身的静态点线间关系进行研究，也要着重考虑模拟攻击对整体路网动态运行的影响，本文采取2类指标进行研究。

2.1.1 静态点线间表征指标

本文将平均度K、度分布P(K)、路网聚类系数C、连通度α作为静态点线间表征指标。其中：K、P(K)、C的具体公式与文献[21]～[22]中的表达式一致。

连通度α是网络宏观表征指标，利用轨道网络的实际边数m与网络理论最大边数mmax的比值[9]反映网络整体发展模式及程度，n为网络中的总节点数。

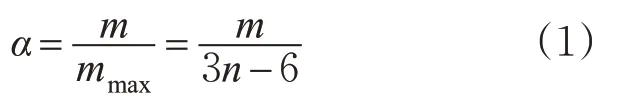
显然，α∈( 0 ，1)。对于既定网络，网络实际拥有边数越多，α值越大，遭受攻击时更具稳定性，且α值与网络的发展程度呈正比关系。

2.1.2 动态稳定性表征指标

动态表征指标中的网络效率E(G)和最大连通子图比率LCC在网络受到攻击时，更明显的表现了网络整体变化趋势，且本文定义E(G)中参变量γ，方便在单节点蓄意攻击时找到网络脆弱节点。

1）网络效率E(G)。网络效率E(G)用于体现最短路径下网络节点间传递、交换信息的效率。本文给出的E(G)计算公式见式（2），n′为网络中有效节点。

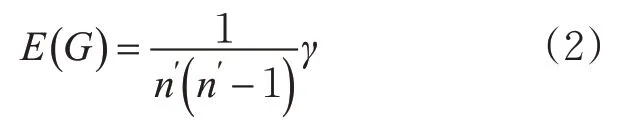
其中

式中：aij为节点i，j间最短路径，参变量γ为节点i，j间最短路径倒数之和。定义Δγi为节点i因攻击失效，原网络中的γ与现有网络间的差值。

因对网络进行单节点蓄意攻击时，只对某1节点进行失效处理，网络中的n′恒定为n-1，任意1次E(G)的计算，其分母为n-1(n-2)，所以简化计算，只计算Δγi可以直观反映节点i对于整体网络的重要程度。

2）最大连通子图比率LCC。网络遭受攻击致部分节点失效后，完整网络被分割成多个互不联系的子网络，其中弧边连接数、节点数最多的子网络定义为最大连通子图。最大连通子图的节点数n0与原网络节点总数n的比值定义为最大连通子图比率LCC，反映了网络全局的连通性。LCC越大，遭受攻击时网络被破坏程度越低。

2.2 攻击方式

在对线网进行抗毁性分析时，大多数研究将复杂网络一般面临的攻击分为：随机攻击（random attacks）和蓄意攻击（malicious attacks）[15]。蓄意攻击又被细分为单节点蓄意攻击（single-node deliberate attack）以及累计节点蓄意攻击（cumulative-node malicious attacks）。随机攻击指随机选择网络中的节点进行攻击，主要反映网络自身容错能力的大小；累计节点蓄意攻击是指1次性攻击特定的1个或多个节点，本文每次攻击选择现有网络中最大度节点。这2种攻击方式下，被攻击的节点无法自我修复，直至网络中的所有节点都被攻击[9，13，23]。以下简称随机攻击为R攻击，累计节点蓄意攻击为CM攻击。单节点蓄意攻击指：对单一节点进行攻击。对网络中单个节点失效处理后，恢复原本节点功能再对下1个节点进行失效处理。在构造拓扑网络的基础上，将基于R攻击、CM攻击、单节点蓄意攻击3种攻击方式对不同规模路网进行模拟攻击。

不同特点的线网攻击对应了发生在现实交通运营中不同类型的突发事件，根据线网攻击的特点及突发事件成因，本文进行分类的结果见表1。

表1 突发事件与网络攻击对应关系Tab.1 Relationship between the emergency and network attack

技术设备类突发事件的成因主要是设施设备年久失修或人员操作不当造成的设施失效损坏，这和自然灾害在不同站点会造成程度不同的突发事件一样，是随机发生的；爆炸袭击、乘客在站点发生意外造成站点停运、发现可疑物品等治安类突发事件既可以发生在单一站点、也可能发生在多个人员密集、节点度大的站点；列车脱轨、列车追尾等运营故障类事件会造成成片区域甚至整条路网的崩溃；大型集会、节假日和重大赛事引起的大客流一般发生在特定站点。

3 典型城市轨道网络抗毁性分析

随着城市轨道交通的迅猛发展，它迅速、便捷、准时、性价比高的特点使得越来越多的市民选择城市轨道交通出行，但这也要求突发事件发生后，应急系统必须快速准确的评估事件对线网的影响并做出正确应对措施。笔者将10个典型城市轨道交通路网作为研究对象，模拟突发事件对不同规模网络稳定性、抗毁性的表现情况。10个城市线网规模分为2类。规模1：运营线路在10条以上的较发达线网；规模2：运营线路在5～10条的发展中线网。轨道运营线路过少的城市因线路无法构成复杂网络，不具备参考价值。

3.1 网络基本特性

城市轨道交通线网信息经本文图1步骤处理后得到各城市拓扑空间。S，n，m，K通过操作Pajek软件功能键获得，C由文献[22]中关于路网聚类系数的公式计算可得，α通过式（1）运算获得，E(G)通过Matlab计算γ并带入式（2）运算获得。提取整理的各表征指标见表2，其中S为轨道网络线路数；L n为换乘站点数。

由表2数据可知，城市轨道交通路网规模对表征指标的影响很大。构成城市轨道交通的站点与线路越多，网络平均度越大，网络连通度越高。数据显示现阶段上海和深圳的表征指标都较好的反应了网络稳定性和通达性。连通度最大的城市是上海，达到0.396，即占据各点完全连接的39.6%，在考虑连通度的同时，也需要考虑建设成本和地形地势对城市轨道路网的影响。网络聚类系数显示，虽然深圳轨道交通网络规模远小于北京，但其网络存在较多换乘枢纽站且线路站点间构成更多三角形结构，使得深圳轨道交通网络的连通度和运营效率表现更优。

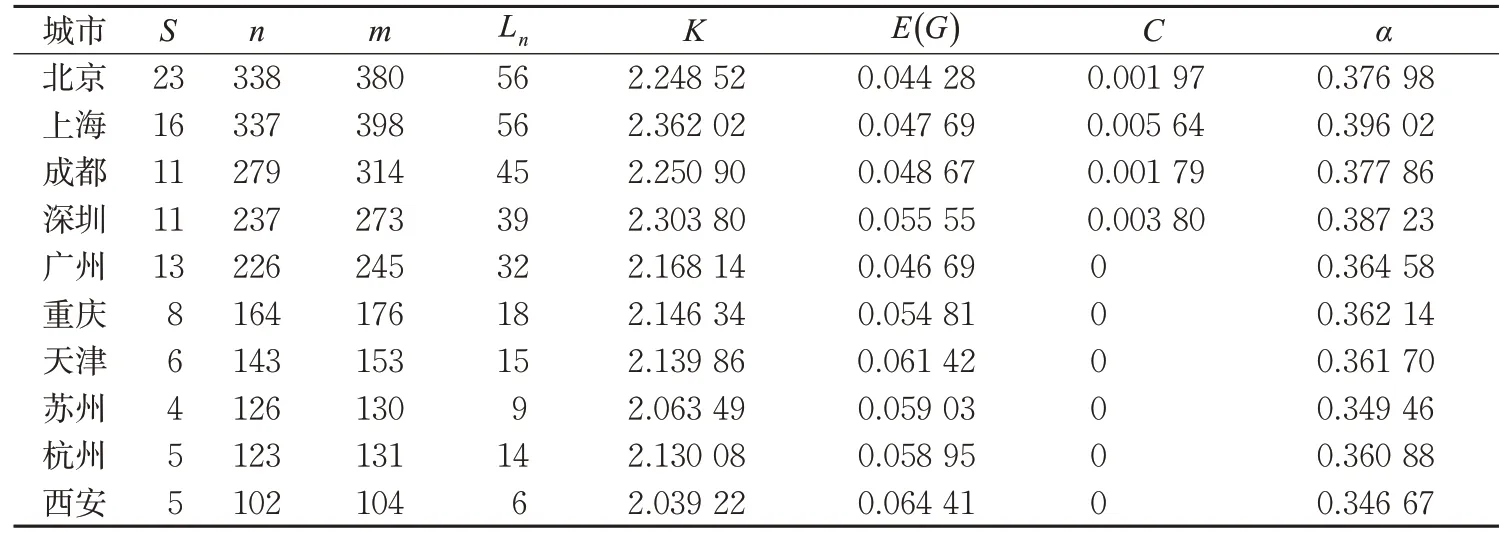
表2 各城市轨道交通网络静态表征指标Tab.2 Static representation indices of the metro network in China

以上述网络构建和原始指标为基础，利用Matlab的Distances函数对10个城市进行模拟攻击。在对网络进行5组R攻击、5组CM攻击后取各指标平均值作为本文研究数据。处理各城市线网中不同节点度所拥有的站点数所得到图3，虽然路网规模不同，对应节点度纵轴站点数各不相同，但不同城市的节点度分布（下文简称为度分布）趋势基本一致，说明城市间未受攻击时的度分布性质相似。对网络度分布进行拟合，因加入K=1的节点导致拟合结果较差，且网络节点的幂指数函数分布不显著，所以舍去K=1的节点，只用Matlab对度分布尾部进行拟合[9]。以图4为例，对深圳市度分布尾部进行拟合，得到式（6）的幂律分布拟合函数，其拟合优度R2=0.9 847。

图3 各城市原始节点度分布Fig.3 Degree distribution of original nodes in cities

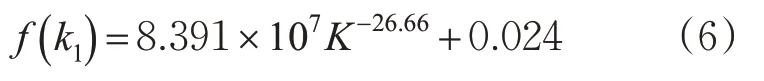
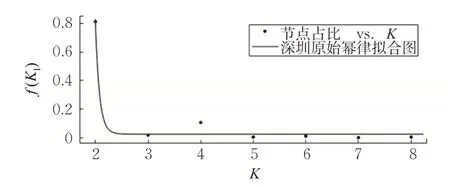
图4 深圳市原始度分布幂律拟合图Fig.4 Power-law fitting of original degree distribution in Shenzhen

R2趋近于1可知，深圳的度分布尾部函数高度拟合幂律分布，证明深圳轨道交通网络具有无标度网络特点，这与文献[4]的结论相符。使用相同方法对剩余9个城市进行度分布尾部拟合得到表3，R2均大于0.97，拟合程度极好，说明此次研究的10个城市轨道交通网络都具有无标度网络特性。

表3 各城市原始度分布尾部度分布拟合函数Tab.3 Tail-fitting function of each city's original degree distribution

3.2 R攻击和CM攻击下网络抗毁性分析

整理被攻击后各城市的节点度数，得到图5和图6。此时的度分布趋势已和原始度分布有较大区别。

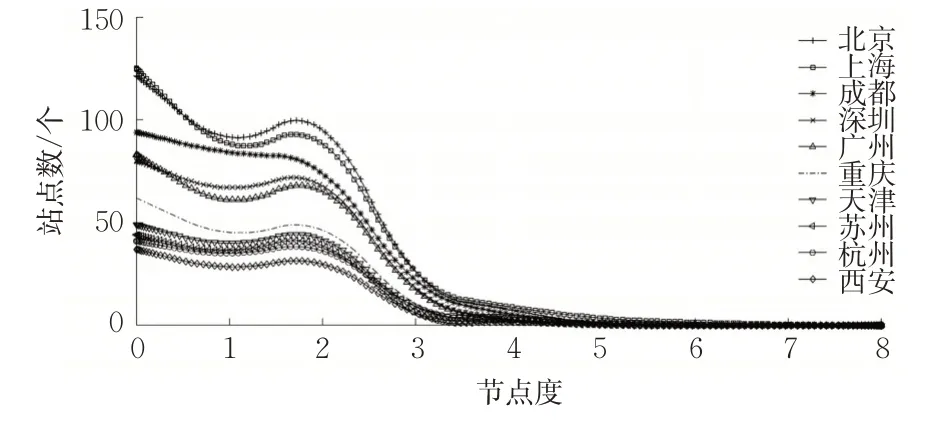
图5 R攻击下各城市剩余节点为70%的节点度分布Fig.5 Degree distribution of remaining 70%nodes in cities under R attack

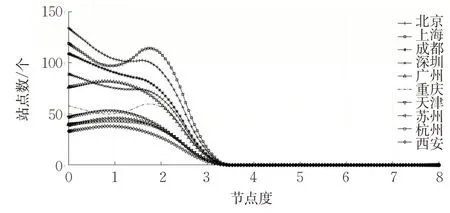
图6 CM攻击下各城市剩余节点为75%的节点度分布Fig.6 Degree distribution of remaining nodes 75%in cities under CMattack

同样以深圳市的城轨线网为例，对其R攻击剩余70%节点后的度分布和CM攻击剩余75%节点后的度分布进行拟合，得到图7～8，以及拟合函数见式（7）～（8）。

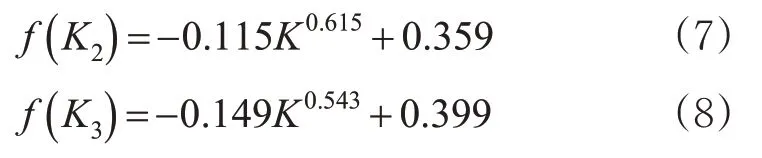
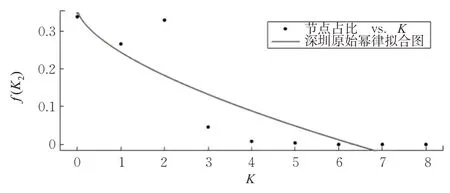
图7 深圳R攻击70%个节点后度分布幂律拟合图Fig.7 Power-law fitting of remaining 70%nodes degree distribution in Shenzhen under R attack

图8 深圳CM攻击75%个节点后度分布幂律拟合图Fig.8 Power-law fitting of remaining 75%nodes degree distribution in Shenzhen under CMattack

此时的拟合函数虽依然满足幂律分布，但与原始度分布的拟合函数相比K前系数从正数变为负数，说明经过攻击，拓扑网络性质已经改变，不能承担原网络的运营任务，所以本文用以分析的数据截取R攻击前30%节点和CM攻击前25%节点这个区间内。且由表4可知各城市在2种攻击下，拟合函数都发生了改变，且拟合度有所降低。

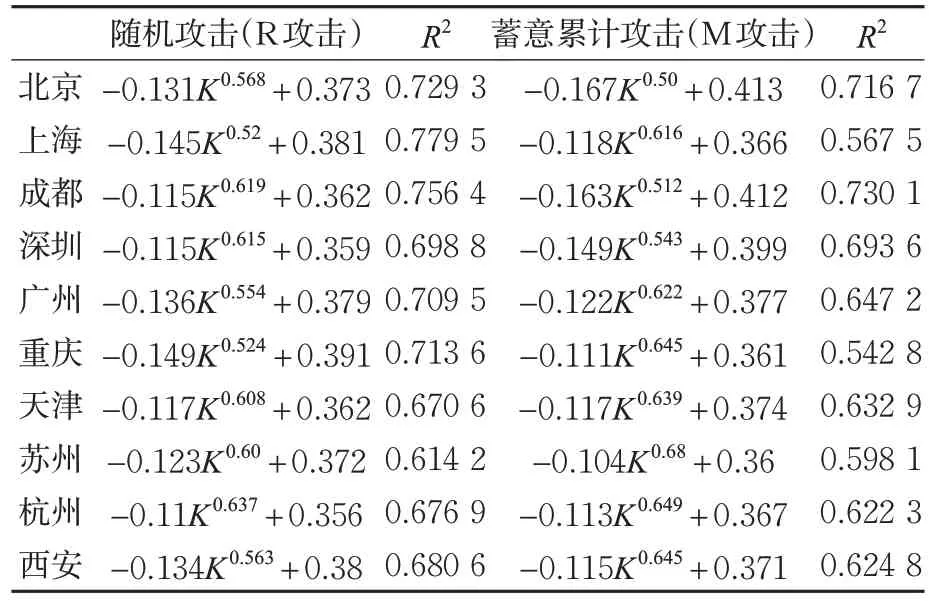
表4 各城市模拟攻击后尾部度分布拟合函数Tab.4 Tail-fitting function of each city's degree distribution under attack

3.2.1 节点度分析

由图9（a）可知各城市在R攻击下K呈现均匀的直线下降趋势，节点度与城市轨道交通规模复杂程度在攻击前后都基本成正比，K均在1以上且R攻击前10%节点时，K平均下降16%。图9（b）显示在CM攻击下，各城市K也基本呈现直线下降趋势，但比R攻击下降速度更快。CM攻击前10%节点时，K平均减少了33%，部分城轨网络在攻击结束后K小于1。

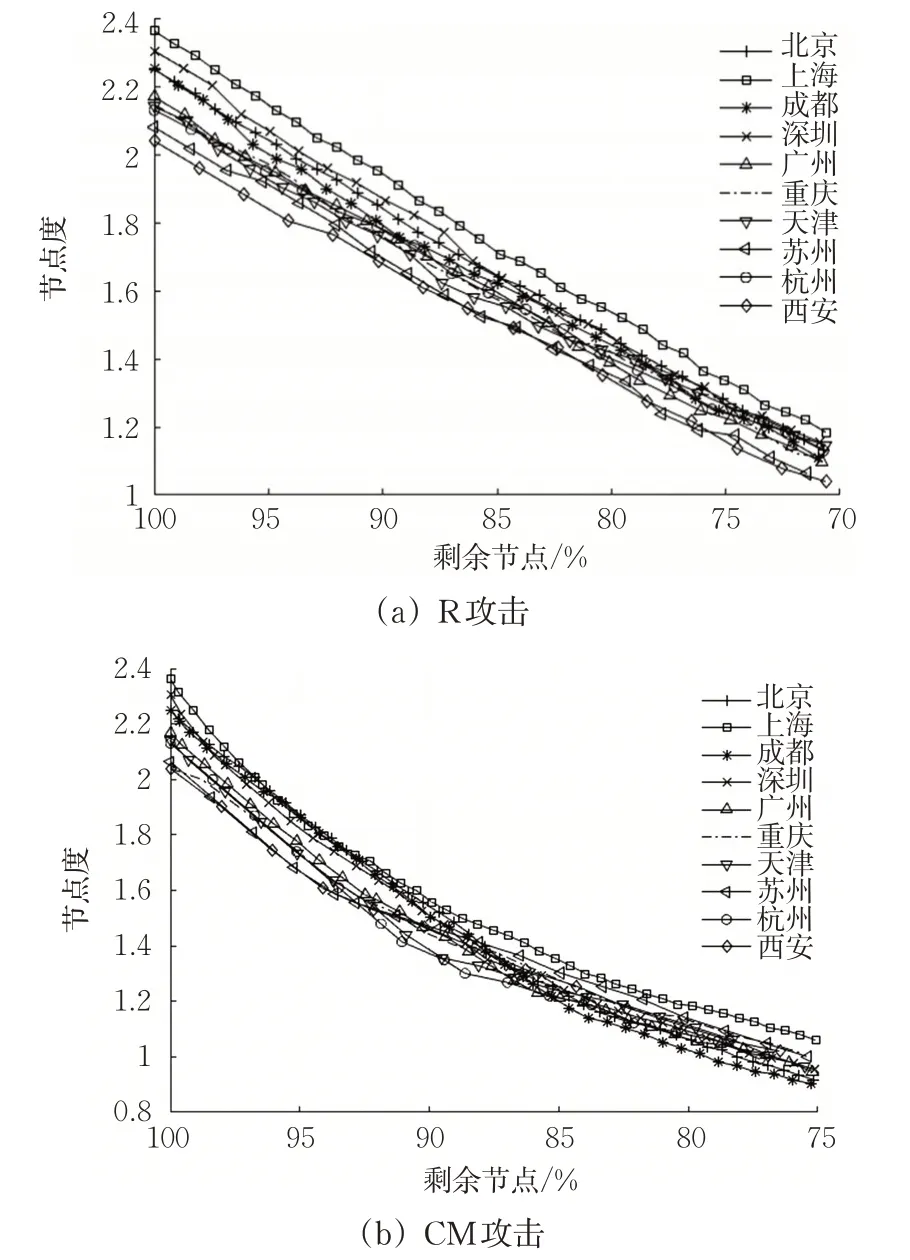
图9 2种攻击下各城市变化趋势Fig.9 Variation trend of under two attacks in cities

每攻击1次，各城市的平均失效边经过计算得到图10。CM攻击首先攻击K值大的节点，证明CM攻击相比R攻击，节点度K的下降趋势明显更大。R攻击下网络规模越大，平均失效边越多；CM攻击下城市的L n越多平均失效边越多，例如，杭州轨道网络规模虽然不大，但因Ln相对更多，其失效边数高于广州。

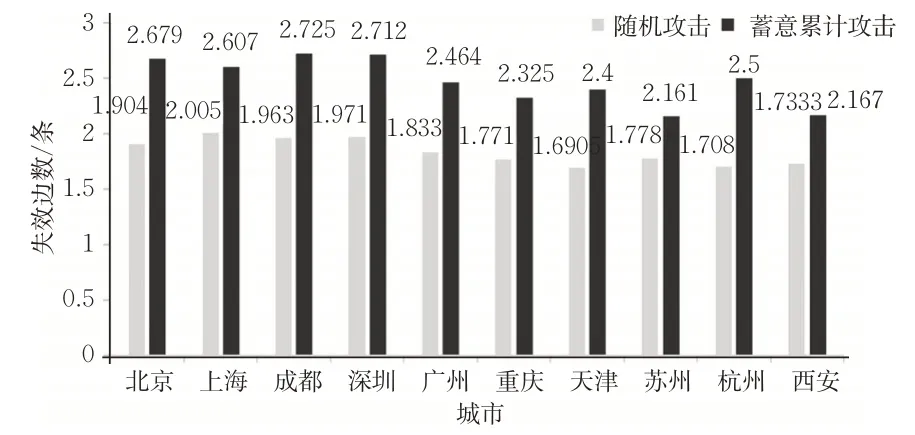
图10 1次不同攻击下各城市平均失效边Fig.10 Average edge failure for each city under different attacks

3.2.2 连通度分析

由图11中各城市的连通度α变化趋势对比可知：R攻击下各城市α基本呈现均匀线性下降，且在攻击30%个点后α平均减少0.11。CM攻击下α呈下降趋势，如北京、成都网络连接边较少但换乘节点较多的城市网络连通度相对下降更快，且在攻击25%个点后规模1的城市α平均减少0.17、规模2的城市α平均减少0.13。说明CM攻击下，α下降的更快且对路网发达城市影响更大。

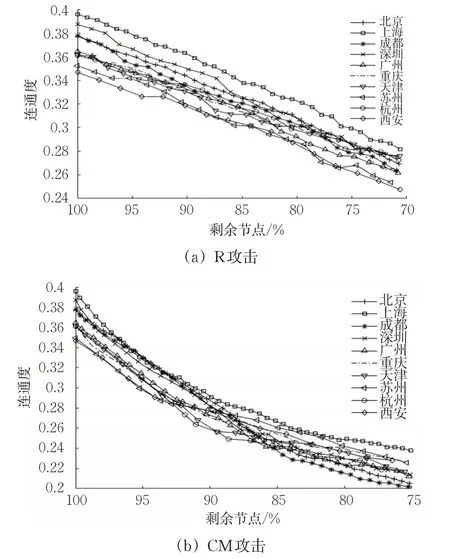
图11 2种攻击下各城市变化趋势Fig.11 Variation trend of under two attacks in cities

3.2.3 网络效率分析

由图12各城市网络效率变化趋势图对比可知：城轨网络面对R攻击显示了更好的稳定性，被攻击5%个节点时大多数城市的网络效率保持在原效率的80%以上，被攻击10%个节点后，各城市E(G)保持在原效率的60%以上。而CM攻击5%个节点后，大多数城市的E(G)陡降至原效率的30%左右，被攻击10%个节点后，各城市E(G)下降至原效率的20%左右。说明关键节点（即节点度大于2，现实路网中为换乘站）的失效，极大的影响整体轨道网络效率。

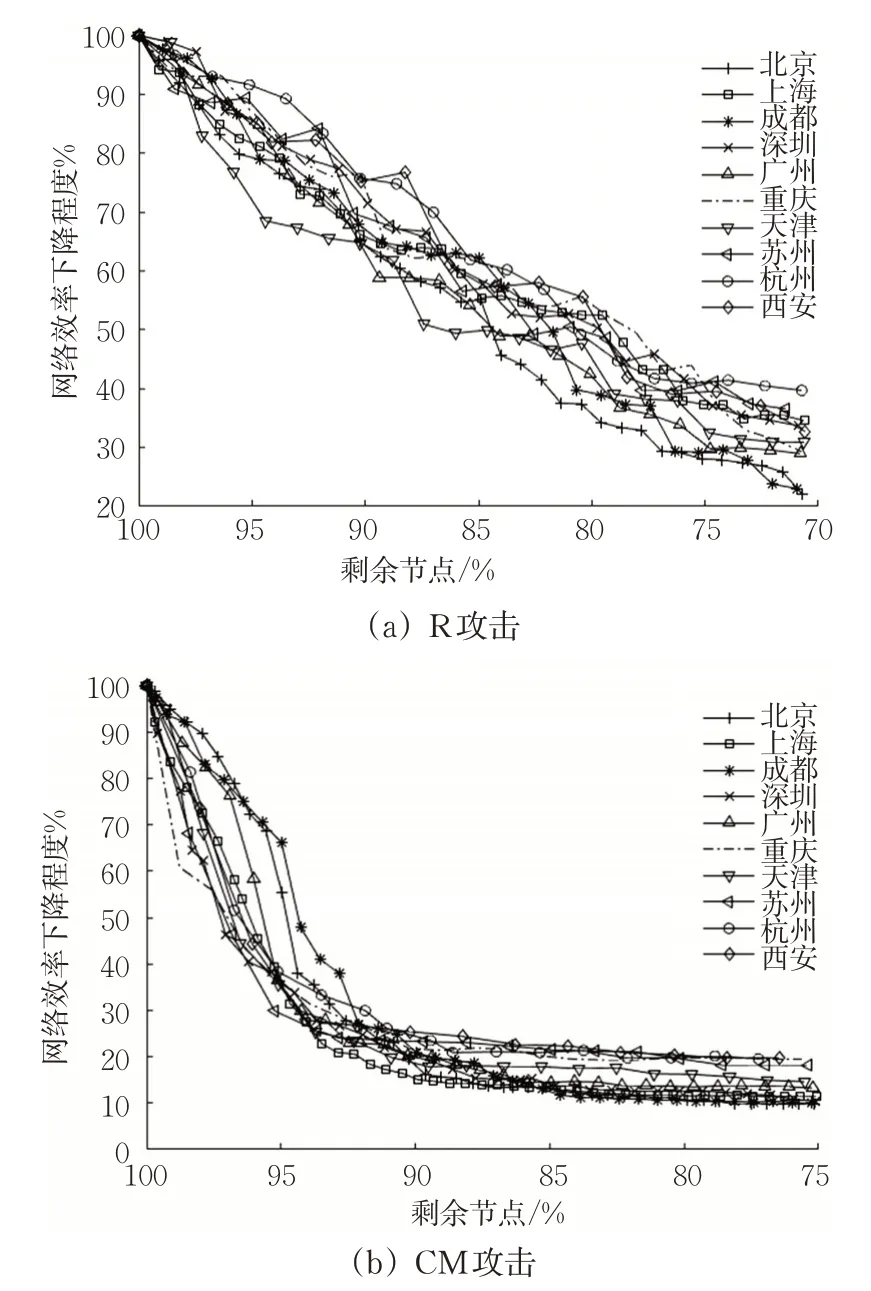
图12 2种攻击下各城市变化趋势Fig.12 Variation trend of under two attacks in cities

3.2.4 最大连通子图比率分析

由图13可知，在攻击到关键节点时，网络越密集、越发达，可以连通的子图比率越大。R攻击10%个节点时，各城市的LCC大部分保持在原始比率的65%以上，而CM攻击在攻击10%个节点后，各城市LCC基本降至原始比率的20%～10%。进行前1%～2%个节点CM攻击时，LCC的变化极小，但失效点累计一段时间后，网络中某几个关键节点的失效会极大影响LCC。

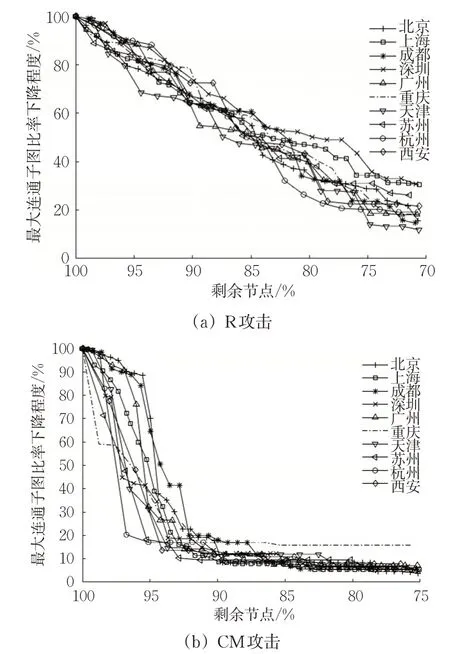
图13 2种攻击下各城市变化趋势Fig.13 Variation trend of under two attack in cities

3.2.5 不同规模网络的指标边界

将10个城市的2 075个站点作为研究对象，规模1网络平均有节点283.4个，规模2网络平均有节点131.6个。根据上述指标分析可以得到不同标准下2种规模路网的平均失效节点占比（指标边界）。其中设定平均度达到初始网络的80%、网络效率达到原始效率的50%、LCC达到初始网络的60%时路网崩溃[14]，它们的失效节点数占比可对应为路网崩溃的指标边界。具体数据见表5～6。

表5 R攻击下不同规模网络指标边界Tab.5 Network-index boundary of different scale under R attacks%

对比表5和表6可知：以规模1的节点度为例，R攻击下的边界为10.44%，CM攻击下的边界为5.22%，CM攻击较R攻击对网络的破坏力更强，CM攻击的特点对换乘站的数量、所处位置、线路的数量更敏感。以K、E(G)、LCC为分析指标，R攻击下，它们在规模1路网的指标边界为10.44%，17.99%，13.27%，规模2路网的指标边界为：11.09%，18.38%，12.92%，2种规模路网指标边界重合度较高，R攻击结果与网络规模大小基本无直接关系；CM攻击下，规模1路网的指标边界为5.22%，4.3%，4.23%，规模2路网的指标边界为：5.17%，3.19%，2.43%，规模1路网的各指标边界均高于规模2的，说明在CM攻击下下不同规模的路网间指标边界有差距，且规模较不发达路网对关键节点失效更敏感。

表6 CM攻击下不同规模网络指标边界Tab.6 Network index boundary of different scales under CMattacks%

3.3 蓄意单节点攻击下网络抗毁性分析

利用Matlab对各城市网络进行蓄意单节点攻击，计算每个节点的参变量Δγi，得到图14。对应真实站点所处位置观察图14中Δγi，可以找出一些典型点。例如图15（a）的上海轨道交通网络图，标号为40的站点K40=4，Δγ40=59.1；同在上海，图15（b）显示标号为269对应的站点是11号线和16号线的换乘站罗山站，标号为47的站点是2号线、7号线和16号线3条线路的换乘站龙阳路。2个站点对应的节点度和效率参变量分别为：K269=4，Δγ269=404；K47=5，Δγ47=391.8。可知K一致的节点，对网络效率的影响却差别极大。图15（c）所示北京轨道交通图中标号为201的节点也可证明，它的节点度虽然只有4，但14号线和燕房线通向网络中心时都必须通过七里庄。这使得201号节点成为北京轨道交通网络中Δγi最大的节点。

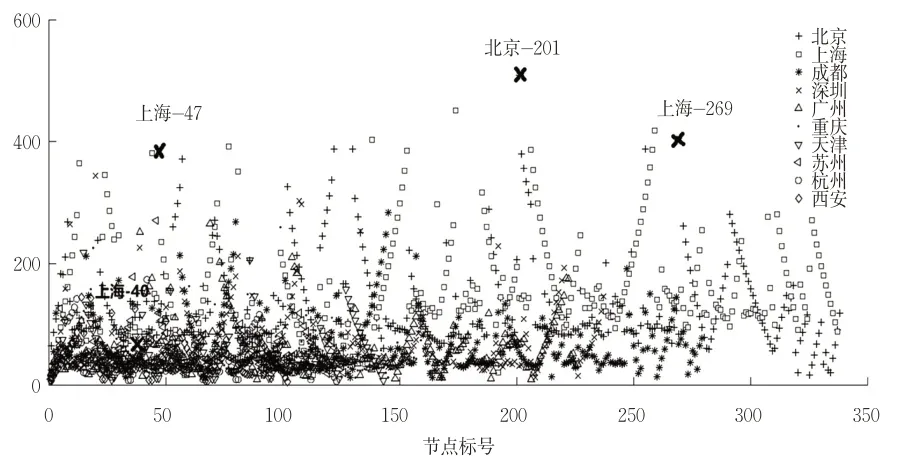
图14 单节点蓄意攻击下各城市影响趋势Fig.14 Variation trend of under single-node malicious attacks in cities

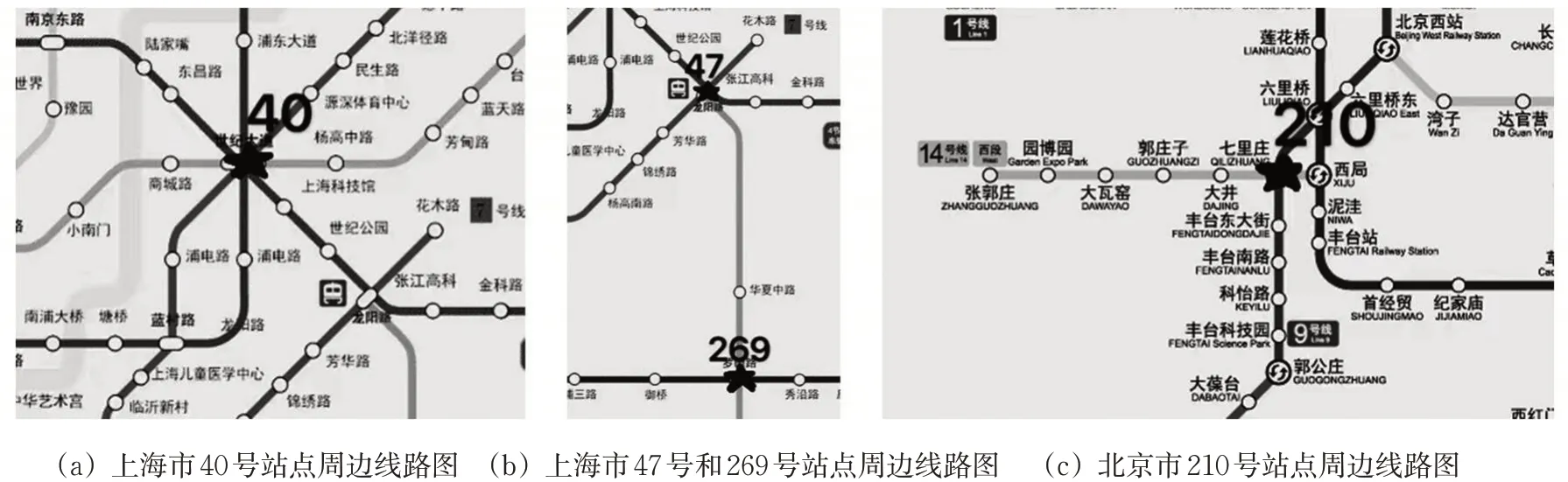
图15 城市轨道交通局部标点图Fig.15 Local punctuation of an urban-rail transit

对以上节点信息总结可知：若被攻击点位于网络核心延伸支线，则距离网络密集中心越远的点Δγi越小，对整体网络效率影响越小。当攻击关键节点时，节点在网络中所处位置的不同，对整体路网效率的影响也不同。关键节点的关联节点彼此有高频率的连线、所处在三角形结构或网状结构内，它的失效对于整个网络正常运行影响较小。当关键节点处于多条路线交点且路线呈发散式，以交点为圆心一定范围内的路线间再无其他节点相连，这时关键节点的失效将极大的影响着网络效率。