超临界二氧化碳溶胀天然橡胶动力学分析*

2021-07-29王贝贝夏浩海王晓冰邓晓清

弹性体 2021年3期

宋琪，王贝贝，夏浩海，王晓冰，李翔，邓晓清**

(1．长江大学化工与环境工程学院，湖北荆州 434023；2．长江大学机械工程学院，湖北荆州 434023)

超临界二氧化碳(ScCO2)是一种新型绿色溶剂，在化工生产过程中受到越来越多的关注。它既具有液体的溶解性，又具有气体的渗透性，广泛应用于萃取分离、有机物合成、废弃物降解、新染色工艺开发、材料发泡和微粒制备以及干燥与清洁等领域[1-6]。相比于传统溶剂，ScCO2具有诸多优势，如价格低廉、环境友好、不易燃易爆、环境状态下易与高分子材料分离等[7]。

在高分子材料领域，ScCO2通常作为反应溶剂或者增塑剂，应用过程中包括大分子或者小分子的质量传递[8]。ScCO2和高分子材料形成的两相体系中，二氧化碳分子向高分子材料内部扩散，产生溶胀现象，溶胀的高分子链段空间构型发生变化，其物理特性也会相应地发生变化[9]。因此，有必要分析ScCO2在高分子材料中的扩散和高分子材料的溶胀过程。

溶胀最显著的特点是材料表观尺寸的变化，可以通过直接观测的方法分析高聚物吸收以及解吸溶剂的过程[10]。溶胀动力学就是溶剂吸附量随时间的变化，是一个扩散过程。对于玻璃化转变温度以上的高聚物，溶剂分子的扩散速率小于交联网络大分子链的松弛速率，为Fickian溶胀过程。对于玻璃化转变温度以下的高聚物，聚合物链的松弛速率缓慢，溶剂分子的扩散速率更快，为non-Fickian溶胀过程[11]。溶剂在玻璃态高聚物中的扩散可以观察到明显的扩散前沿，直观地分析溶剂的扩散距离，通过Fick定律确定扩散系数[12]936-938。而对于玻璃化转变温度以上的高聚物，溶剂的扩散过程中只能观察到样品尺寸的整体变化。Crack基于Fick第二扩散定律，推导了矩形、球形以及展开平面的扩散方程[13]40，据此可以计算高弹态高聚物中的溶剂扩散。

一些学者研究了ScCO2在高分子材料中的扩散过程，Lemert等[14]研究了聚异戊二烯橡胶在ScCO2中的溶胀过程，样品为非硫化橡胶，没有观察到详细的尺寸变化。Kojima等[15]178-181在此基础上分析了球状硫化的聚异戊二烯橡胶的溶胀过程，观察了溶胀尺寸的变化。辛晓等[16]也采用同样的方法分析了圆柱状硫化天然橡胶在ScCO2中的溶胀过程。通过以上方法可以得到ScCO2在橡胶高分子中的扩散系数，但是均没有详细分析交联密度以及溶胀温度、压力等因素对于扩散的影响规律，并且没有从动力学角度分析扩散过程。有鉴于此，本文制备了不同交联密度的天然橡胶样品，通过溶胀动力学分析了不同温度下ScCO2在橡胶高分子中的扩散过程。

1 实验部分

1.1 原料

天然橡胶：云标1#，云南南泰橡胶有限公司；硫磺：分析纯，阿拉丁试剂(上海)有限公司；氧化锌、硬脂酸、促进剂CZ：分析纯，阿拉丁试剂；甲苯：硫化橡胶交联密度测量溶剂，分析纯，国药集团化学试剂有限公司；二氧化碳：分析纯，武汉纽瑞德特种气体有限公司。

1.2 仪器及设备

高温高压可视反应釜：UF-200-30，江苏联友科研仪器有限公司。材料为316 L，设计温度200 ℃，设计压力为30 MPa。CCD相机：istav DH 734-18F-03,Andsr实验设备简图如图1所示。

图1 可视窗反应釜简图

1.3 实验方法及过程

实验过程中，首先将胶球悬空置于高压反应釜中部，关闭反应釜盖，二氧化碳由柱塞泵输入反应釜内，通过多次置换以除去反应釜内空气，之后将反应釜加压到预设压力。加热装置为电加热炉，升温速率为3 ℃/min，随着温度的升高，压力逐渐增大，到达目标温度所对应的压力即为目标压力。温度和压力测量传感器精度分别为-0.1～0.1 MPa。反应釜两侧有石英玻璃可视窗，由于溶胀作用胶球在ScCO2中体积逐渐变大，通过连续拍摄胶球体积增大过程，进而采用图形软件分析胶球的溶胀程度。

1.4 硫化橡胶样品的制备

制备不同交联密度的橡胶球，具体配方如表1所示(按质量份计)，为了便于分析采用最简化的配方，不含任何油和填料。橡胶球初始半径为7 mm，胶球交联密度根据Florye-Rehner方程计算[17]。样品A和B的交联密度分别为0.78×10-4mol/cm3和1.9×10-4mol/cm3。

表1 天然橡胶混炼胶组成

2 溶胀动力学分析

溶胀动力学研究橡胶在溶剂中的溶胀速率，也就是胶球表观体积变化速率，时间t时刻溶胀率St表达式如式(1)。

(1)

式中：V0为(目标温度下)未溶胀橡胶体积，mm3；Vt为溶胀t时刻后橡胶的体积增量，mm3；r0为(目标温度下)未溶胀橡胶半径，mm；rt为(目标温度下)溶胀t时刻后橡胶的半径，mm。通过对溶胀度进行拟合，分析适合溶胀过程的经验方程。

2.1 溶胀动力学方程

分析溶胀速率变化符合一阶或二阶动力学过程，一阶动力学方程如式(2)所示。

(2)

式中：S是时间t时刻的溶胀率，Se是溶胀达到平衡时的溶胀率，K1是一阶溶胀动力学常数，由溶胀速率和dS/dt和剩余溶胀能力Se-S的比例求得。式(2)积分可得方程式(3)。

(3)

ScCO2中胶球溶胀二阶动力学方程如式(4)所示。

(4)

从时间0到t积分式(4)得到式(5)。

(5)

K2是二阶动力学常数，K2减小溶胀过程变慢。二阶动力学方程系数由式(5)较难直接获得，可拟合回归方程快速求得，如式(6)所示，由截距b1即可求得K2。

(6)

拟合系数b0和b1如式(7)、式(8)所示。

(7)

(8)

式中：自变量x为溶胀时间t，因变量y为t/St。

均方根误差RMSD分析回归模型和实际值之间的偏差，如式(9)所示。

(9)

式中：ycalc为预测值，yi为实验值，n为实验数据点数量。均方误差越小，预测值和实验值差别越小，模型越准确。

2.2 二氧化碳扩散系数

通过可视窗可以观察溶胀程度随着时间的变化，在此基础上计算二氧化碳在橡胶中的扩散系数。二氧化碳的扩散过程是气体分子向高分子链段之间的自由空间迁移的过程。环境温度在高分子材料的玻璃化转变温度以上时，溶剂分子向高分子体的扩散速率低于高分子链段运动的驰豫时间，溶胀过程由扩散步骤控制，二氧化碳的扩散对于橡胶的溶胀起决定作用，扩散过程遵循Fickian扩散机制。相反地，环境温度在高分子材料的玻璃化温度以下时，扩散速率比高分子链段运动的驰豫时间大，溶胀过程由网络大分子链的松弛速率决定，扩散过程为non-Fickian扩散机制。根据Fick定律，二氧化碳向胶球样品的迁移过程如式(10)所示。

(10)

式中：r为胶球中心到球体某一点的距离，C为样品内溶剂的溶度，D为扩散系数。当样品为球形，半径为a时，Crank求得了该方程的解析解[13]52。

(11)

式中：Mt和M∞分别代表时间t和达到溶胀平衡时胶球内吸收二氧化碳的量。当t值较大，胶球接近溶胀平衡时，方程式(11)近似等于式(12)。

(12)

溶胀过程做如下假设：(1) 二氧化碳从胶球表面移动到中心的距离为半径a，由下文研究可见，溶胀导致胶球的体积变化率并不大，因此这一假设不会导致显著的误差；(2) 二氧化碳被橡胶球吸收后立即导致其体积发生变化。基于以上假设，结合式(1)可得：

(13)

式中：St和Se分别为t时刻和溶胀平衡时的溶胀度，合并方程式(12)和式(13)得：

(14)

(15)

(16)

2.3 发泡橡胶回缩速率

ScCO2中充分溶胀的橡胶，一定速率泄压会导致橡胶发泡，内部形成空隙，外部尺寸变大。恢复环境状态后，由于硫化后的橡胶具有三维体型结构，发泡的橡胶会逐渐收缩，t时刻发泡橡胶膨胀度收缩到Sst。

(17)

收缩过程动力学表达式如式(18)所示。

(18)

积分上式得式(19)。

(19)

式中：Ss0和Sst是发泡后0时刻和t时刻胶球膨胀度；K3是收缩速率常数。

3 结果与讨论

ScCO2中溶胀前后橡胶如图2所示。由图2可见，溶胀后橡胶尺寸变大，且整体形状依然呈现球形，未出现流动和形状变化异常等情况，因此可以通过观察尺寸的变化分析溶胀过程。

(a) 溶胀前

(b)溶胀平衡溶胀条件：温度为50 ℃，压力为16 MPa图2 通过可视窗观察胶球的溶胀情况

3.1 胶球溶胀分析

不同温度下胶球的溶胀规律如图3所示。溶胀温度分别为50 ℃和120 ℃，压力为16 MPa。由图3可见，溶胀温度为50 ℃时，240 min达到溶胀平衡；而温度为120 ℃时，120 min即达到溶胀平衡。根据分子热运动理论，高温导致二氧化碳分子的扩散性增强，高分子链段的移动性也会增强，因而温度越高，胶球达到溶胀平衡的时间越短。温度50 ℃达到溶胀平衡时，样品B的溶胀度低于样品A，样品B的交联密度为样品A的2.4倍，更多的交联位点使橡胶大分子链受到更多的束缚，从而溶胀度更小。然而，随着温度的升高，交联密度更大的样品B的平衡溶胀度增大，样品A的平衡溶胀度变化不大。温度为120 ℃时，样品B的平衡溶胀度与样品A相近，并且120 ℃时样品的溶胀度要高于50 ℃时。根据Kojima的研究[15]175-181，二氧化碳密度和样品溶胀度正相关，而随着温度的升高，相同压力下二氧化碳的密度是降低的。显然，温度对于胶球的溶胀也有一定的影响。当温度较高时，胶球受热膨胀与溶胀作用共同使其体积增大。

t/min(a)

t/min(b)图3 天然橡胶球在ScCO2中溶胀度随时间的变化

3.2 溶胀动力学分析

根据溶胀动力学方程所得实验结果如图4所示。由式(3)和式(6)可知，如果溶胀过程符合动力学方程，实验值拟合后是一条直线。然而，当溶胀时间低于60 min时，一阶和二阶方程计算实验数据的线性度均较差，并且由图4(b)可见，0～60 min时二阶方程完全不呈线性趋势。产生这一现象，是由于0～60 min属于程序升温阶段，该阶段的溶胀属于升温溶胀，而不是等温溶胀，因此动力学拟合结果较差。溶胀温度为50 ℃时，由于目标温度较低，而反应釜功率是一定的，当温度接近50 ℃时，温升较慢，所以温升阶段接近100 min。

等温阶段的反应动力学分析如图5所示，由式(3)和式(6)线性拟合等温溶胀阶段实验数据，拟合度R2如表2所示。由表2可见，一阶和二阶动力学方程均能较好地预测溶胀过程。温度为50 ℃时，溶胀过程符合二阶动力学过程，而当溶胀温度升高到120 ℃时，溶胀过程更符合一阶动力学过程。

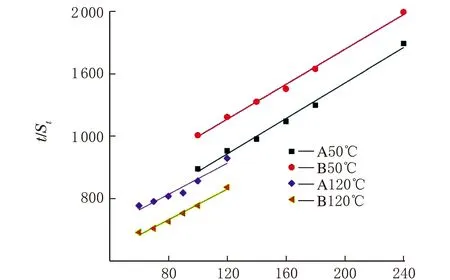
t/min(b)图5 天然橡胶球在ScCO2中一阶(a)和二阶(b)溶胀动力学拟合曲线

表2 溶胀动力学方程拟合度R2

反应动力学常数K如表3所示，K1和K2分别代表一阶和二阶动力学方程。随着温度的升高，K1和K2均显著增大，表明溶胀速率加快。这一结果与图3一致，图3中随着溶胀温度的升高，胶球更快达到溶胀平衡。

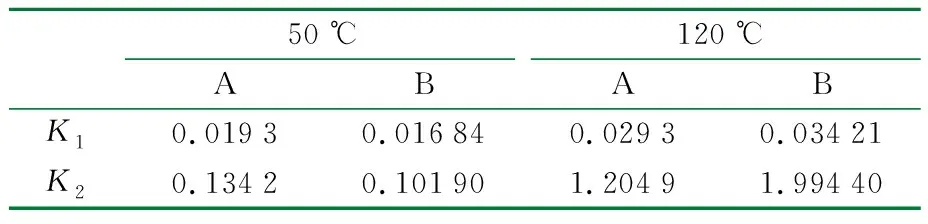
表3 溶胀动力学常数K

由式(9)计算动力学拟合方程的RMSD，结果如表4所示，均方根误差和响应值相比差距均较小，表明模型的预测值ycalc和实际实验yi值吻合度高。

表4 式(6)回归方程系数和RMSD

3.3 二氧化碳在胶球中的等温扩散系数

t/sa

t/sb图6 不同温度溶胀时间t随ln(1-St/Se)的变化

表5 二氧化碳在天然橡胶球中的等温扩散系数

3.4 发泡胶球收缩动力学分析

天然橡胶球在ScCO2中达到溶胀平衡后，以一定的速率泄压，本研究的泄压速率为0.5 MPa/min，由于橡胶所处环境压力降低，橡胶内吸收的的气体由于内外压差快速膨胀，导致橡胶发泡。样品A发泡前后尺寸对照如图7所示，原胶球直径为14 mm，发泡胶球直径为31 mm。

溶胀条件：温度为50 ℃，压力为16 MPa，时间为6 h图7 溶胀前后天然橡胶球尺寸

发泡后的橡胶从反应釜取出置于环境状态下，如图8所示，膨胀度随时间的增加线性减小。根据式(19)，ln(Ss0/Sst)随时间的变化如图9所示，直线斜率即为收缩速率常数K3，样品A和B的收缩速率常数分别为5.14×10-6min-1和7.11×10-6min-1。样品B的交联密度是样品A的2.4倍，而ScCO2中平衡溶胀度相近，但发泡后的膨胀度分别为9.7和6.3，且样品B的收缩速率比样品A高38%。

t/min图8 不同交联密度橡胶膨胀度随时间t的变化

t/min图9 ln(Ss0/Sst)随时间t的变化

可见，交联密度对于橡胶在ScCO2中的溶胀过程并无显著影响，但是对于发泡后橡胶的膨胀率以及收缩速率有显著影响。Nikitin报道[12]939，交联密度增大到一定程度，吸收二氧化碳的量并无太大差别，因而溶胀度差别不大。但膨胀后橡胶的交联网络伸展，分子排列趋于有序，根据熵增原理，高分子链有收缩、卷曲、无序化的趋势，因此交联密度大的橡胶，由于大分子链段受到更多的束缚，膨胀率更小，收缩速率更快。