核心问题设计,助推思维发散
——基于学生思维发展的数学核心问题设计
2021-07-29福建省龙岩市松涛第二小学廖景贵
福建省龙岩市松涛第二小学 廖景贵
核心问题是核心素养背景下提出的教学理念,即围绕学生思维发展模式,致力于落实三维教学目标,在深刻理解教学内容和深入、客观地分析学生学习情况的基础上,设计的引领学生开展学习活动的关键性问题。对于高年级的小学生来说,已经具备了一定的数学基础与思维能力,但思维能力还存在较大的局限性,还需要进一步强化。小学高年级数学不仅是小学数学教学的进一步深化、拓展,同时也是初中数学教学衔接的重要途径。在这个阶段渗透数学思维,能使学生逐渐养成科学合理的数学思维模式,进一步提升数学能力的同时,为初中更为抽象的数学知识学习奠定扎实的基础。而核心问题在思维能力培养方面具有得天独厚的优势,基于学生思维发展进行数学核心问题设计,无疑成为教师研究的重要内容。
一、对话教材,提炼核心问题
核心问题的设计,围绕小学数学教学目标、教材、学生等方面开展,而教材当中往往蕴藏着各式各样的核心问题,教师所要做的就是针对教材进行深入挖掘,提炼教材当中蕴藏的各种核心问题,为学生数学思维发散奠定良好的基础。在备课过程中,对于教材的分析挖掘,要透过现象去掌握各个问题的本质,致力于从原本表面不存在关联的各种事物当中去摸索各种潜在的联系。在此基础上,将教材当中蕴藏的各种明线功能利用起来,以此来探索一些隐性的数学本质,再通过梳理各种完全分散的知识体系,将数学思想渗透于核心问题的设计中。
例如,以“小数除法解决问题”为例,备课中教师应当摆脱传统的思维模式,避免传统“灌输式”的教学模式,尝试从学生的角度去分析教材,综合参考学生的知识体系、生活体验,针对教材内容挖掘学生在实际学习进程中会面临怎样的困难,最终设计符合学生已有生活阅历、思维模式的核心问题。具体来说,学生对于小数除法较为陌生,且相关概念相对较为抽象,教师可以将教材中的知识凝练出来,提出两个学生生活中熟悉的例题进行核心问题设计:(1)我们需要将21kg的大米分别装入不同的袋子中,而每个袋子只能够装下2.5kg,需要准备几个袋子?(2)用34分米的丝带来包装礼盒,而一个礼盒的包装需要使用丝带2.5分米,能够包装多少个礼盒?由于没有接触过相关概念,学生在解决问题的过程中一头雾水,只能够列出算式:21÷2.5=8.4,34÷2.5=13.6。教师并不需要急于公布答案,而是再次提出解决问题的方法:大家生活中经常去超市购物,生活中大家是怎么解决的呢?对于第一个问题,袋子都需要取整数,大家该怎么选取近视值呢?大部分学生这个时候想到了“四舍五入”,即21÷2.5≈8个。然后教师引导学生从实际经验着手,提问:8个袋子是否能够装下21kg的大米?学生思考以后,很快就能够得出8个袋子只能够装下20kg的大米,还剩余1kg的大米,最终需要使用9个袋子。这个时候教师引出概念,让学生结合生活实际进行思考,并引出“进一法”的概念。对于第二个问题,同样采用相似的方法,学生也能够理解“去尾法”的概念。最后,教师再引导学生讨论什么情况需要“四舍五入”,什么情况需要“进一法”,什么情况需要“去尾法”。如此,学生不仅能够进一步学习“小数除法解决问题”的核心知识,同时也能够理解数学与生活之间的密切联系,思维也在这个过程中得以有效锻炼,可谓一举多得。
二、趣味设计,调动思维兴趣
众所周知,兴趣是最好的老师,尤其是对于小学生来说,是否存在兴趣,对于学习效果会产生巨大影响。思维能力的培养,同样需要注重学生兴趣的培养。学生保持浓厚的兴趣,才会自主思考、自主探索,实现思维发散的目标。因此,对于小学数学核心问题设计来说,必然需要兼顾学生学习兴趣,在教学过程中围绕学生这个主体,设计一些“现实的、有意义的、创新的且具有挑战性的问题”,同时在教学过程中搭建促进学生思维发散的教学情境,基于情境搭建来激发学生思维兴趣,让学生在自主思考、小组探究中思维相互碰撞,完成探索与学习。
例如,以“平面图形面积的整理与复习”教学为例,教学导入环节,设计以下核心问题:(1)你会计算哪个图形的面积呢?(2)你能选择一个图形来展示一下它的面积公式推导过程吗?(3)根据刚才面积计算公式的推导过程,可以发现这些平面图形之间有什么联系呢?学生通过自主思考、小组讨论,最终在黑板上结合教具摆出知识网络图(图1)。
教师提出问题,回顾我们刚才整理的过程,根据知识内在的联系,整理成这样的知识网。通过上述设计,学生经历回顾与交流的过程,在讨论、操作、比较中梳理平面图形面积公式的推导过程,体悟转化思想,感受知识间内在的联系。多样知识结构图的展示,让学生感受到了它的作用,掌握了这一梳理知识的方法,并将它运用到今后的知识梳理中。在此基础上,教师提出核心问题:它们都可以用梯形的面积公式来计算,你知道为什么吗?通过观察、辨析、交流、想象等活动,以梯形面积公式为线索,引导学生将梯形的上底缩短为零或延长到一定量时,梯形就变成三角形、平行四边形、长方形等图形,根据上底的长度变化,梯形面积计算公式就可以推导出三角形、平行四边形、长方形等图形面积公式,把各种面积公式内联,将分散的知识点串成一串,实现知识间的重新组织与整体建构。通过上述核心问题的设计,不仅能够将学生的思维兴趣充分调动起来,同时可以让学生在这个过程中发散思维,巩固平面图形的面积推理过程,并掌握一定的思维规律。
三、问题延伸,助推思维拓展
理论与实践相结合历来是教学中不可或缺的。学生思维能力的发展,同样需要保持理论与实践的有效结合,将核心问题设计延伸到课外,让学生利用课外的时间在生活中检验课堂知识,并在完成问题的过程中拓展自身思维空间,不断发散学生思维。就小学数学教学而言,核心问题设计延伸到课外也是教学中至关重要的环节,通过有针对性的课后练习设计,可以让学生在这个过程中进一步巩固课堂所学知识,回顾课堂中的思维模式,同时了解自身在学习过程中暴露出来的问题。所以,课后核心问题的设计,教师应当通过问题引导学生回顾课堂思维、建立新旧知识的联系,同时分析课堂学习过程中存在的各种问题,让学生在温故而知新的过程中巩固学习成果。
例如,完成上文所述“平面图形面积的整理与复习”教学以后,设计练习拓展,提出核心问题:下面的图形(图2)面积是一样的吗?请说说理由。通过“面积一样吗?”,引导学生体悟“等积变形”。学生在观察、比较、推理过程中,运用平移、旋转等图形的运动形式进行深入思考、深度说理。这在综合应用所学知识的同时,也能发展学生的有据推理能力和空间想象能力,培养学生的空间观念。
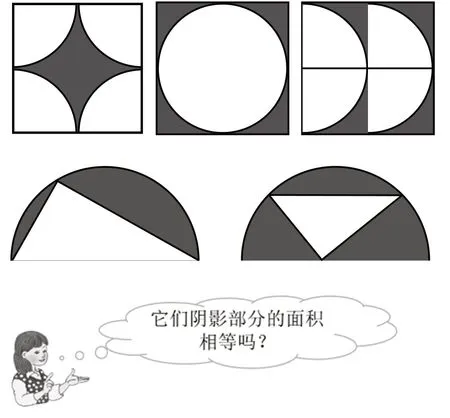
图2
总的来说,核心问题设计作为核心素养培养中的一项重要内容,迎合了小学数学教学目标、小学生思维发展需求,能让学生在核心问题的引导下,实现综合能力的全面提升。在教学过程中,教师应重视学生数学思维的培养,同时充分结合新课改要求、小学数学教学目标要求,通过对话教材提炼核心问题、趣味设计调动思维兴趣、问题延伸助推思维拓展,将核心问题渗透到小学数学教学的各个环节,让学生在核心问题的引导下,通过自主探索、思维碰撞、集思广益的学习过程,促进思维的发展、发散。
