面向变电站机器人巡检路径规划中的算法研究
2021-07-28王秀丽侯静楠王仕俊
王秀丽,周 鹏,侯静楠,王仕俊,林 霞
1.山西大学 电力工程系,太原030013
2.国网甘肃省电力公司 经济技术研究院,兰州730050
3.国网山西省电力公司,太原030021
目前变电站的巡查中,无人化逐渐成为一种趋势,巡检机器人的应用将越来越广泛。文献[1]中介绍了当前巡检机器人的发展现状,指出了当前仍然存在的问题,比如巡检路径的问题。文献[2]中提出使用AMCL(Adaptive Monte Carlo Localization)算法进行定位,但分类讨论的情况不够充分。文献[3]中提出使用A*算法,但该算法在计算过程中当存在多个最小值时不能保证路径最优,存在局部最优问题。文献[4]中提出改进的Dijkstra算法,该算法具有全局最优的特点,但时间复杂度高,耗时长。文献[5]中提出改进的遗传算法,效率提高但也存在一定问题,即精度存在偏差,路径不一定最优。
在巡检车或巡检机器人巡视的路径规划中,可以将该问题看作是旅行商问题(Traveling Salesman Problem,TSP),目前有很多智能算法,比如动态规划法、分支限界法、Dijkstra 算法、A*算法、蚁群算法、模拟退火算法、遗传算法等,前两种主要适用于小规模的TSP,后三种主要适用于大规模的TSP。
在变电站巡检机器人巡视的路径规划当中主要解决三种问题:(1)全局巡检,即从出发点到目标点(即为返回点)的正常巡视,在本文中采用一种新的算法完成;(2)多点巡检,即固定设备巡视,采用Dijkstra 算法和遗传算法相结合的方式使其通过规划能顺利经过必须巡视的设备;(3)单点巡检,即突发情况巡视及应急返回,采用Dijkstra算法来完成该任务。
主要针对以上三种情况分别做了设计和仿真验算。
1 变电站建模
在对变电站的分析中,选取具有典型代表的矩形网状分布模型,如图1所示。

图1 变电站模型
根据以上思路,作如下假设:
定义一个典型的变电站Sr,c,g,设存在r行,c列设备组,每组g台设备分别在设备中心靠近道路侧及道路分支处选取点作为特征点,如图1所示。
对于一个变电站Sr,c,g,定义特征点集:

对于所有特征点之间的道路有边集:
E={所有道路}
定义图Gr,c,g=(V,E),Gr,c,g可以用于表示变电站设备区的道路结构。
从变电站的布局特点不难得到,图Gr,c,g有以下特点:
(1)Gr,c,g是无向无环的;
(2)Gr,c,g是加权的,权重反映相邻顶点间的距离;
(3)Gr,c,g是连通的,且没有孤立点;
(4)∀v∈V,4 ≥deg(v)≥2。
同时可以发现,对于任意大小的变电站模型,均可认为是图2最小单元的重复。

图2 最小单元示意图
故对某一变电站的研究可以推广到所有的同类变电站。下文将以变电站S4,5,3为例探究变电站路径的规划算法,模拟地图以某一中型变电站设备区作为模拟对象,地图大小6 900×2 250 px,比例尺1 m=100 px。地图共设有操作柜60 台,分为20 组,4 行5 列分布。每台设备周围均有多个巡检点。所有模拟路线图中,巡检车的进场位置均位于(0,0)位置。
2 全局巡检中新哈密顿算法的提出
对于全局巡检问题,很容易想到:巡检机器人不重复地走完所有的特征点,就可以使巡检路径最短。在数学上可以表示为求取图Gr,c,g的哈密顿回路,由离散数学的知识可以得到,目前还不存在有简单的判定哈密顿回路存在的充要条件,故只能对此问题做如下分析:
经过图中所有顶点一次且仅一次的回路称为哈密顿回路,对应于图2的哈密顿回路即为绕其所有顶点的外边框。
再分析如图3 所示的变电站S2,2,2,也可以很容易地找到一个哈密顿回路,如图4所示。

图3 变电站2模型

图4 对应变电站2模型的哈密顿回路
可以从上看出,对于任意的Sr,c,g都存在哈密顿回路,哈密顿回路可以通过以下归类来建立。
令起点h0=v0,j0,对于起点为h0的回路H,其中的任一点都满足以下两种状况:
(1)当n=0 时有:

式中,hn为属于回路H当中的任一节点。
(2)当n≠0 且令hn=va,b(a为当前巡视节点所处的行数,b为当前巡视节点所处的列数,且a,b均大于等于0),此时有以下几种情况:
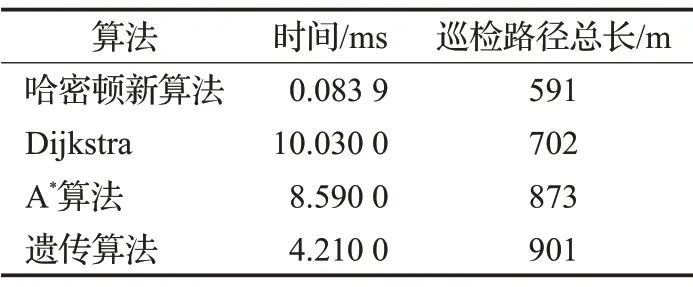
若0 若a>0 ∧amod 3=0 ∧bmod(g+2)=1 ∨(amod 3 ≠0 ∧bmod(g+2)=g+1),此时有: 若(amod 3=2 ∧bmod(g+2))∉{0,g+1}∨(a=3r-1 ∧bmod(g+2))=0,此时有: 若a>0 ∧amod 3=0 ∧dmod(g+2)∉{0,1},此时有: 若a=0 ∧b>0,此时有: 由上对S4,5,3进行路径规划,得出巡检机器人的全局巡检路径如图5 所示,巡检总长:59 100 px=591 m,×代表起点。 图5 全局巡检示意图 图6 为全局巡检流程图,设定巡视起点h0等于v0,j0,定义一个变电站Sr,c,g,并将其带入哈密顿回路公式计算,之后进行判断,若hn=v0,j0,即可输出全局巡检的路径[6-9]。 图6 全局巡检的流程图 对以上新算法与几种传统常规方法全局巡检的结果进行比较的结果,见表1所示。 表1 全局巡检仿真结果比对 从以上仿真数据结果可以看出,采取的哈密顿新算法具有仿真运算时间相对较短和巡检路径相对较优的特点。 变电站中的多点巡检,指对固定设备的巡视,这里主要采用Dijkstra算法和遗传算法相结合的方式使其通过规划能顺利经过必须巡视的设备。 Dijkstra算法算是基于贪心思想而来,用于单源最短路径的求取。其原理是将起点到所有点的路径存储,经松弛操作后将最短距离的点作为中转点,并将最短距离更新,直到扩展到终点为止。具体算法思想如图7所示[10]。 图7 Dijkstra算法原理图 遗传算法是一种全局优化概率算法,也是一种搜索启发式算法,是进化算法的一种。这种启发式通常用来生成有用的解决方案来优化和搜索问题。遗传算法的基本运算过程如图8所示[11]。 图8 遗传算法运算过程 为解决运算节点过多而导致遗传算法中的基因数量和遗传次数增加的问题,这里提出Dijkstra 算法和遗传算法相组合的方式,即在初始阶段采用Dijkstra算法,求出每两个目标节点之间的最小路径,再用遗传算法求解到达每个目标节点的先后顺序。 在变电站巡检过程中,多点巡检是指对固定设备或重点设备的巡视,主要采用Dijkstra 算法和遗传算法相组合的方式来应用。以变电站S4,5,3为例探究变电站路径的规划算法[12-13]。 (1)电量充足时的多点巡检仿真 当对重点设备巡检过程中,电池电量充足时,路径规划的流程图如图9所示。 图9 电量充足时多点巡检的算法流程图 图10 为电量充足时多点巡检路线的仿真结果图,巡视完的路径长度:13 252 px=132.52 m。图中×为变电站巡检入口,圆点表示重点巡视的变电站设备。 图10 电量充足时多点巡检路线仿真结果图 (2)电量不足需返回充电时的仿真结果 当对重点设备巡检过程中,电池电量不足需要返回充电。 图11为一个重新规划了的多点巡检路径图。图12中,红色正方形框代表当巡检到此点时报警提示电量低,此时按照流程图中的算法规划好返回的最短路径,红色线代表紧急返回充电的路径。图13为充电完成后继续巡检剩余重点设备的路径规划图。 图11 多点路径巡检规划图 图12 电量低时的返回路径规划图 图13 充电完成后继续巡检剩余重点设备的路径规划图 所谓单点巡检,主要指当变电站某处运行出现故障或其他紧急情况时,可通过指派巡检机器人赶至需巡视地点。这种模式要求响应速度快,可以迅速对异常节点进行查看,让相关人员迅速获取异常节点的关键数据。当异常解除后或当工作人员认为不需要继续进行观察时,巡检机器人需原路返回之前的位置点继续执行巡检任务。单点巡检中主要使用了Dijkstra算法,图14为单点巡检时的算法流程图,图15为仿真结果图,其中蓝色点为需要巡检的单台设备,巡视结束后沿原路返回[14-15]。 图14 单点巡检流程图 图15 单点巡检仿真结果图 针对变电站的巡检算法问题进行了研究讨论,本文中设定了三种巡检方式:全局巡检、多点巡检和单点巡检。全局巡检中,提出了一种基于哈密顿回路的新算法,以一个四行五列,且每组三台设备的变电站(变电站可以任意设定设备数量和行列数)为例进行了仿真,结果证明该算法比常规方法的计算速度相对更快,巡检路径相对更短。多点巡检和单点巡检也分别采用相应的算法进行了仿真。本次设计中,创新之处主要体现在全局巡检的算法选择。 以上结果表明,针对小规模的TSP 问题,对路径规划的情况进行分类,可以选择出相应的不同算法,以此 达到优化的目的,本文结果证明算法有效可行,但也存在一些问题,比如选取的变电站主要为矩形设计,如为其他形状时,需要重新修改程序,下一步将继续针对不同形状的变电站路径进行设计,并且找出新提出的算法可以适用的更多的范围。






3 组合算法的提出
3.1 Dijkstra算法

3.2 遗传算法
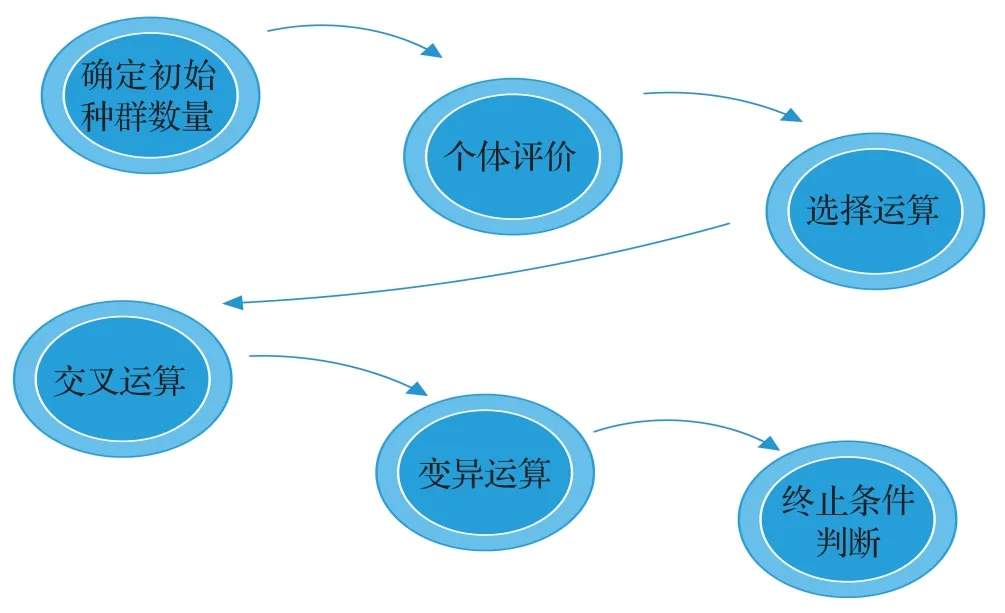
3.3 组合算法的思想
3.4 组合算法在多点巡检中的应用







4 结束语
