二次幂耦合的K-means聚类算法研究

相益萱，姜 合，潘品臣，孙聪慧

齐鲁工业大学（山东省科学院）计算机科学与技术学院，济南250353

所谓数据挖掘就是从大型的数据库中提取有趣的、非凡的、蕴含的、先前未知的以及潜在有用的信息或者模式，随着科技的发展，数据挖掘成为当下用户从大量的数据中提取出来有效信息的手段，并且衍生出了很多分支，其中又以K-means[1]聚类算法作为经典的聚类分析算法。K-means聚类：即是一种无监督的问题，将相似的东西分到一组，不相似的尽量远离。它具有快速、简单的特点，同时它也受初始中心的选择随机性和离群点的干扰可能导致聚类不佳，但是即使存在上述问题，并不影响它被广泛地应用在各个行业的领域。

针对K-means算法存在的问题，许多学者提出一些解决办法，袁方等[2]为了消除传统K-means算法对初始聚类中心敏感问题，提出一种优化初始聚类中心的方法，通过计算每个数据对象所在的区域密度，选择相互距离最远K个处于高密度区域的点作为初始聚类中心，以提高聚类的效果。另外张靖等[3]为了提高聚类稳定性并降低时间复杂度，提出了基于个体轮廓系数自适应地选取优秀样本以确定初始聚类中心的改进K-means算法。邹臣嵩等[4]解决了传统K-means 算法聚类结果随机性大、稳定性差，以及最大距离乘积法迭代次数多、运算耗时长等问题，提出一种基于最大距离积与最小距离之和的协同K聚类改进算法。行艳妮等[5]为了能够及时了解Spark 环境下经典聚类算法K-means 的最新研究进展，把握K-means算法当前的研究热点和方向，针对K-means 算法的初始中心点优化研究进行综述。靳雁霞等[6]针对粒子群优化算法容易陷入局部最优且K-mean 算法受聚类数及初始聚类中心的选取影响较大，提出了一种改进的简化均值粒子群K-means优化聚类算法（ISMPSO-AKM）。徐慧君等[7]由于传统的协同过滤算法存在数据稀疏、可扩展性弱和用户兴趣度偏移等问题，算法运行效率和预测精度偏低。针对上述问题，提出一种改进的Mini BatchK-means 时间权重推荐算法，唐东凯等[8]针对K-means算法对初始聚类中心和离群点敏感的缺点，提出了一种优化初始聚类中心的改进K-means 算法。王义武等[9]为了加快K-means 计算速度和寻找最优聚类子空间提出空间投影在K-means算法中的研究与应用，同类型算法在准确度和计算时间方面都得到了大幅提升。王建仁等[10]针对手肘法在确定k值的过程中存在的“肘点”位置不明确问题，提出了一种改进的k值选择算法能更加快速且准确地确定k值。洪敏等[11]针对K-means 聚类结果会受到初始类中心的问题。研究了不同的初始中心选择方法对K-means型多视图聚类算法的影响，并提出一种基于采样的主动式初始中心选择方法，在聚类精度和效率上取得了较好的折衷。

到目前为止，已公开发表了近千种K-means聚类方法，但是大部分都考虑的是数据之间没有关系，彼此相互独立，互相不影响，然而事实上数据之间存在着一些显著性或者隐藏性的耦合关系，基于这个想法，2011 年操龙兵教授提出了非独立同分布[12]的理论，考虑无论是大数据还是小数据，都要去权衡它们属性的异构（Heterogeneity）和耦合关系（Coupling Relationships），关注它们数据的类型、属性、数据源，考虑它们之间比较复杂的关系、层次、类型等，即非独立同分布性。基于这个思想操龙兵[13]等人又提出非监督学习中的耦合名义相似性，另外在实际应用中，由离散变量和数值变量组成的异构依赖属性随处可见，于是基于这样的背景，Wang 等[14]提出了混合数据的耦合相互依赖属性分析。另外Li等通过引入用户与物品之间的非独立同分布耦合关系提出了一种新的通用耦合矩阵分解模型（CMF）[15]，在推荐系统应用方面进行了研究。Wang等[16]针对耦合聚类集成，在基本集群和对象之间包含耦合关系聚类系统中基簇与对象之间的依赖关系，并提出了一个耦合聚类系统的框架能够有效地捕获嵌入在基簇和对象中的交互，具有更高的聚类精度和稳定性，这也得到了统计分析的支持。

潘品臣等[17]利用非独立同分布，并且结合了双领域思想对Min_max方法进行选点优化，既将属性与对象之间的潜在关系挖掘出来，又在选点上避免选到离群点，以提高聚类效果，但是也有局限性，在考虑耦合关系时仅仅考虑到1次幂，在选取第一个初始点的时候是随机的，而且优化后的Min_max 选点可能出现紧凑的情况，所以会导致聚类效果提升相对有限，本文是在之前该课题研究基础上做出的改进。在挖掘潜在关系的时候考虑到2次幂的情况（具体详见2.1节），并且在对于K-means聚类算法的改进中，提出了一个新的求解密度参数的方法，在传统的求密度参数过程中考虑的是全部点之间的距离求平均值作为平均半径，这样的计算方法比较粗略，本文通过每次考虑一个点与其他点之间的距离和以此求平均值（具体过程详见2.2 节），最后发现在最优高密度区域通过聚类迭代方法选取初始中心点后有一定的效果（具体过程详见3.1节），经过实验分析，在非独立同分布下二次幂耦合的聚类迭代方法在准确率、迭代次数、聚类效果上都有一定的提高，基于以上提出了二次幂耦合的K-means 聚类算法研究（Study onk-means clustering algorithm of quadratic power coupling，Q-CKmeans）。

1 K-means算法

K-means算法是由MacQueen提出的基于划分的一种比较流行的算法之一，下面简单介绍该算法的工作流程：

（1）首先从原始的数据中随机初始化选择M个初始聚类中心；计算每个其他的点到这M个点之间的距离，得到M个距离后，根据距离大小将剩余点分配给M个簇，计算每个簇内的质心，将质心作为新的初始聚类中心。

（2）将质心作为新的初始聚类中心后，再遍历其他点到质心之间的距离进而求得新的质心，两者进行比较。

（3）循环步骤（2）直到质心不再发生变化。

这里本文用平方误差和作为判断条件，如公式（1）：

其中，M表示已知需要聚类的个数，m表示每个簇内样本总个数，Pij中i表示i个簇，j表示簇内第j个样本，Ci代表的是第i个簇的质心。

2 Q-C-Kmeans算法

首先将数据集的对象设置为uk,k属于(1,L),L代表样本个数，属性列设为ai,i属于(1,n),n表示属性的列数，然后本文利用修改后皮尔森相关系数，这是由于皮尔森只描述了变量之间具有连续属性的线性关系，但是这样是不全面的，因此希望将n个连续属性以2维展开，然后通过研究每两个更新属性之间的相关性来揭示连续属性之间的耦合关系，这种方法也满足LI 等[18]思想，以便于能够更好地表达出它的耦合关系。

2.1 生成属性间具有平方交互关系的数据集

在这里利用Blood部分数据集为例，介绍非独立同分布的平方交互关系，如下是UCI中Blood数据集的一个片段，6个对象，其中4个属性分别表示R（最近一次捐款的月份），F（捐款次数-捐款总数），M（金钱-捐血总数），T（时间-第一次捐款后的月数），最后一列代表是否献血的二元变量（1 表示献血，0 表示不献血）分为两类，具体如表1。

表1 Blood数据片段

将属性进行平方如表2所示，经过扩展后得到新的属性表，捕获连续属性的内部耦合和属性间外部耦合交互关系，将ai与aj之间的皮尔森相关系数计算出来，如公式（2）：

表2 二次幂后的Blood数据片段

本文将ai和aj代表不同的属性列，L为数据集中所有个数，fi(u)是ai对应的所有属性值，fi(u)是属性aj对应的所有属性值，μj是aj这一属性列的对应均值，然后考虑p_value值检验属性之间不相关的假设。修改后的皮尔森相关系数如公式（3）：

2.1.1 内部耦合属性的计算方法

2.1.2 外耦合属性的计算方法

2.1.3 对象的耦合表示

F代表属性列的最高次幂，其中⊕代表Hadamard 积，⊗表示矩阵乘积。

λ具体值为：

其中，λ表示一个1×F的向量。如表3 所示是经过Zsorce 归一化后的结果（保留了小数点后3 位数）具体的实验结果不用四舍五入。

表3 二次幂耦合后的Blood数据片段

2.2 密度参数和聚类迭代选点思想

本文针对之前该课题存在的一些不足做出改进，其中构建密度参数的方法最初的来源是赖玉霞等[19]的密度思想，经过参数调整后得到最优的高密度区域，以及根据最大距离积[20]的选点尽可能分散的思想，提出一种聚类迭代的方法，在高密度区域选取密度最大点作为初始点，相比本团队潘品臣的方法中随机性选择第一个点会更加稳定，本文将距离高密度区域中初始点最远的点作为第二个点，将前两个点进行聚类迭代产生两个质心之后，选取距离两个质心最远的点作为第三个点，以此类推，由于聚类迭代的过程中会产生簇，本文考虑到如果一个簇已经存在了质心，则同一簇中其他点到质心的距离相对较小，那么选择同一聚类中的其他点作为下一个初始聚类中心的机会就会很小，因此选择距离最远的点，目的使得选点尽可能分散，相比本团队之前提出的优化后的Min_max 方法避免了可能出现选点紧凑的情况，以达到较好的聚类效果。另外本文采用的是欧几里德距离来计算方法，以下是相关步骤。

定义1 欧式距离

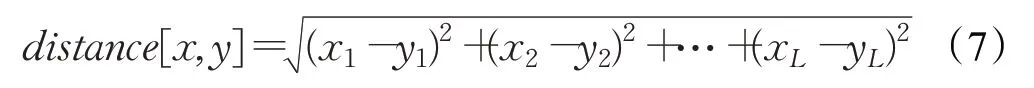
首先本文假设一共有L个样本x1,x2,…,xL,首先计算每个xi样本，i∈(1,L),与其他样本xj,j∈(1,L)之间的距离distance[xi,xi],其中j不等于i。

步骤1 首先设置一个新的集合D1，用来放置每一个点的密度大小，先取出第一个样本xi（这里的xi一次取一个值），计算xi与其他点xj之间的距离，其中j∈(1,L)，用distance(i)表示如公式（8）：

在得到一个集合D1后，求出D1的平均值MEAN_D1,计算在xi周围的点在以MEAN_D1 为半径的内部点的个数作为参考值，具体方式见公式（9）：

得到第一个点的密度大小MIDU(X1)，重复步骤一直到得到全部的点的密度MIDU(Xi)，其中i取(1,L),将密度参数放入，然后求得MIDU(Xi)的均值，如公式（10）：

步骤2 创建一个E集合，用来放置满足大于AvgMIDU一定倍数的xi的样本，这些样本组成高密度区域的点集合E，如公式（11）：

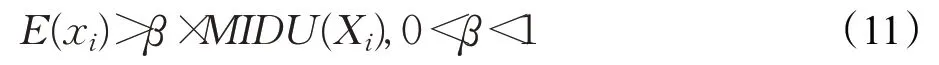
2.3 选取初始中心点

本文在初始中心点的选择上提供了一种聚类迭代的方法，具体的方式如下所示。

Begin：数据样本集L，聚类的个数K

Over：输出K个聚类的中心点M

First：将密度最大的点设置为第一个初始聚类中心点M1

Second：首先进行遍历，计算高密度区域中距离M1的每一个点xi，计算它们之间的距离，将离M1 最远的点设置为第二个初始聚类中心点M2。如图1所示。

图1 选取两个初始中心点

假设图1是高密度区域，其中M1、M2 分别代表已经确定的两个初始聚类中心点。

Third：以这两个点作为中心，然后根据中心与其他点之间的距离，生成两个簇，先求得两个簇的聚类质心C1,C2 在高密度领域求距离到这两个聚类中心点的最远的点，设置为第三个初始聚类中心点，如公式（12）所示：

其中，m代表高密度区域内样本点的个数。如图2 所示，其中C1、C2 分别代表以M1 和M2 为中心，聚类后的质心，在高密度区域中选择距离C1 和C2 最远点作为第三个聚类中心点M3。直线表示两点之间的距离。

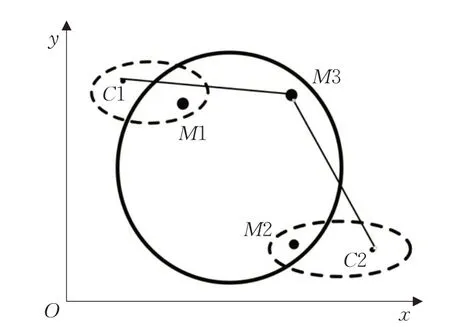
图2 选取三个初始中心点

如果需要分离到四个簇，则先求得前面三个选定聚类中心点的聚类中心，并且在高密度区域的选择距离这三个点的最远处的点作为第四个点，如公式（13）所示：

这个过程会一直进行下去，直到初始集群中心的数量等于预定义的集群数量M。最后，将K-means算法应用于M个初始中心点，使得初始中心点的选择尽可能分散。

2.4 算法描述

综上所述3个过程，接下来，给出算法的具体描述。

Begin：样本数据集L，聚类个数M

Over：得到聚类的M个簇

First：对于样本数据集L，依照2.1节中的计算过程，首先对样本数据集的每一列进行平方，然后计算得到新数据集每一列的属性相关系数（具体公式详见2.1 节），使得能够反映连续属性的全局耦合关系。

Second：根据2.2节中提供求解新密度的方式，得到相应的密度值参数，以及各自的半径平均值，通过调整两个参数得到一个相对合理的高密度的领域。

Third：在高密度的区域，选取密度最大的点作为第一个样本点，选取距离密度最大的点作为第二个点，剩下的点利用聚类迭代后的选点方法进行选点，直到选择的中心点满足M个点。

Fourth：将得到的点带入改进的算法。

3 仿真实验

实验环境硬件：Intel®CoreTMi7-6700CPU@ 3.40GHz，8 GB 的内存；Python3.6，Pycharm2017。实验采用的数据集：本文选用UCI 中的Parkinsons、Blood、Planning、Vertebal数据集，如表4所示。

表4 测试数据集的信息

本文主要是在文献[17]基础上进行的改进，同时本文选用3个比较经典方法，文献[4]、文献[19]以及文献[20]作为参照，主要是三个对比：在非独立同分布下和独立同分布下进行分别比较，非独立同分布下进行比较，以及在独立同分布下进行比较，以此来说明算法的有效性。

3.1 验证聚类准确率的提升

本文的参数选择是通过调整在公式（9）中的α和公式（11）中的β，在实验中本文算法的参数α和β的变化范围都是0～1，参数每次增加0.05来寻找最佳的聚类结果。参数α β的设置上本文建议大致趋向于0.1，0.4，0.9的选择，具体分析（见3.1.1节），表5～8中的N-precision代表在非独立同分布下二次幂耦合的本文算法和经过非独立同分布的一次幂的耦合后利用文献[19]的Min_max 方法、文献[20]中最大距离积方法、文献[4]中的MSDCC 方法，以及文献[17]中的优化后的MIN_max方法进行计算，本文分别在四个数据集上进行比较以此来说明Q-C-Kmeans 算法的有效性，另外precision 代表在独立同分布下的本文聚类迭代方法和文献[19]、文献[20]、文献[4]、文献[17]中各个方法的准确率比较，上述算法的结果都是进行10次实验后取平均值得到的。

表5 Blood数据集上的实验结果

如表5所示在本文的Q-C-Kmeans算法中参数设置为α=0.4,β=0.9,本文利用在非独立同分布下一次幂的方法将数据集处理完后，继续用文献[17]、文献[4]、文献[19]、文献[20]方法进行比较，发现同样在非独立下二次幂的算法的准确率相比其他的文献算法提升了3.1%左右。体现出非独立同分布下的二次幂的优越性。另外很明显非独立同分布下相比独立同分布下的各个数据集的准确率相应地提高3%、1.6%、1.6%、1.7%、1.5%，体现了非独立同分布的优越性，另外在独立同分布下，α=0.9,β=0.4 分别提高1.7%、1.7%、1.8%、1.6%。这说明本文的聚类迭代方法相对于文献[17]中优化后的Min_max方法、文献[19]中的MIN_max方法、文献[4]中的MSDCC 方法、文献[20]中的最大距离积的方法在Blood数据集上准确率的优势，表明本文的方法是可行的。

如表6 所示参数设置为α=0.9,β=0.6 时本文的QC-Kmeans 算法准确率相比其他文献分别提升了2.9%、2.6%、3.1%、2.6%左右，说明了二次幂相对于一次幂的优越性，同样在非独立同分布下准确率相比独立同分布下的准确率也要高，相应提高了6.6%、5.8%、5.9%、6.3%，体现了非独立同分布的优越性，在独立同分布下的本文将参数设置为α=0.2,β=0.7,本文对于初始中心点的优化方法相比独立同分布下的其他方法也分别提高2.1%、1.1%、2.8%、2.6%左右，这说明Q-C-Kmeans中的聚类迭代方法要优于文献[17]、文献[20]、文献[19]以及文献[4]中的方法，表明聚类迭代的思路是有效的。

表6 Parkinsons数据集上的实验结果

如表7所示参数设置为α=0.1,β=0.8 时本文的QC-Kmeans在非独立的二次幂的处理之后准确率相比文献[17]、文献[4]、文献[19]、文献[20]方法在非独立同分布下的一次幂准确率分别提升18.3%、17.6%、18.1%，17.6%，提升非常明显，更加说明了本文非独立同分布下二次幂耦合的有效性，另外本文的聚类迭代算法独立情况下参数设置α=0.8,β=0.1,本文算法的结果相比其他文献的结果分别提升了1.2%、1.6%、1.1%、0%，说明本文聚类迭代的思想的有效性，非独立同分布的相对于独立同分布的结果提高了17.6%、0.5%、1.6%、0.6%、0%。体现了非独立同分布的有效性。

表7 Planning数据集上的实验结果

如表8所示参数设置为α=0.3,β=0.9,本文的Q-CKmeans在非独立同分布下的二次幂耦合相比非独立同分布的一次幂分别提升了12.5%、13.9%、13.3%、14.9%，在独立同分布下中本文设置参数为α=0.95,β=0.15，但是发现独立同分布所给的方法相比非独立同分布高，说明了非独立同分布并不是对于全部的数据集有效，但是本文提出的聚类迭代的方法相对于独立同分布下的其他文献也是有效的，分别提高10.9%、9.6%、12.9%、0.3%。

表8 Vertebal数据集上的实验结果

图3 中可以看出在非独立同分布下二次幂耦合的聚类迭代算法相对于非独立同分布下一次幂耦合的文献[17]、文献[20]、文献[4]、文献[19]中所用的方法，在Parkinsons、Blood、Planning、Vertebal 数据集上有很明显的提升，这主要是得益于本文二次幂的耦合能够更好地将数据之间的潜在关系更好地挖掘出来，从图4 中看出，在独立情况下比较，本文的聚类迭代算法相较于文献[17]、文献[20]、文献[4]、文献[19]中的方法在Blood、Parkinsons、Planning、Vertebal数据集上准确率也有相对比较明显的提升，这得益于本文算法的有效性、合理性。

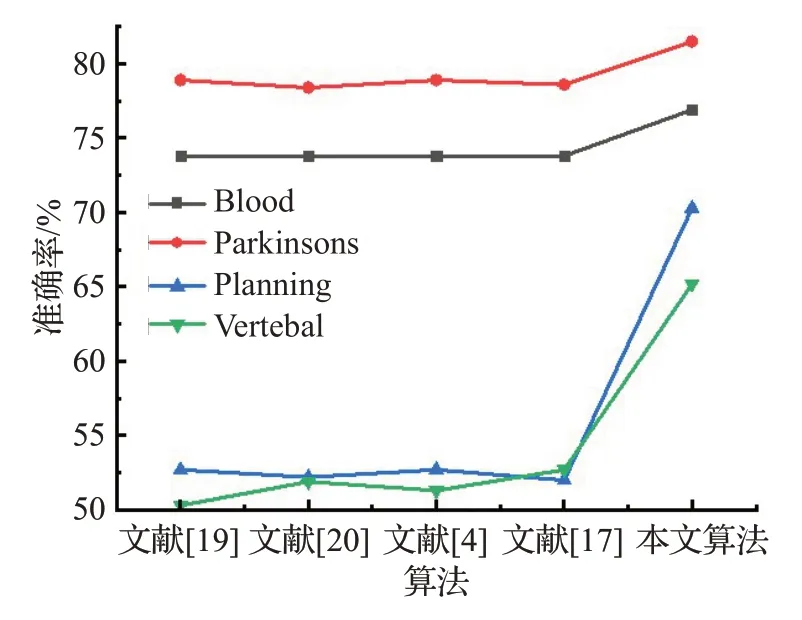
图3 非独立同分布下准确率的对比

图4 独立同分布下准确率的对比

3.1.1 参数的选择

如图5从整体上分析聚类迭代算法的参数选择，横坐标表示参数α、β所选的值，纵坐标表示出现的次数，如图5分析数据集整体在0.1、0.4、0.9的次数比较多，但是本文所实验的数据集只有4个，并未在大量数据集进行验证，相对性根据实验结果给出的参数选择建议在0.1、0.4、0.9附近。

图5 次数比较

3.1.2 复杂度的分析

本文用算法的时间复杂度来说明算法运算量，其中m为数值属性的维度，n为样本数目，k表示聚类数目，t表示K-means迭代次数。

本文算法在非独立同分布下二次幂的内耦合时间复杂度为O(nm2)，外耦合的时间复杂度为O(mn)，对象耦合的时间复杂度为O(mn)，数据归一化的时间复杂度为O(n)，在算法上求解密度参数的时间复杂度为O(mn)，构建高密度的区域的时间复杂度为O(n)，聚类迭代的时间复杂度O(n),K-means 算法O(knt)，所以本文的QC-Kmeans 算法整体上的时间复杂度为O(nm(m+3))+O(n(2+kt))。

在不考虑非独立同分布的前提下本文算法的时间复杂度与文献[20]、文献[19]、文献[17]基本上是同一级别的。

3.2 聚类分析对比

在实验中对非独立同分布下的文献[4]、文献[17]、文献[20]中的方法在四个数据集进行验证分析，实验结果10 次取平均值，本文用聚类的平方误差和判断聚类效果，聚类的平方误差和越小，就说明聚类的效果越好，由于Parkinsons、Vertebal与其他两个数据集的范围相差比较大，所以分成3 个图比较，如图6～图8，另外迭代次数越小，表明收敛的速度快，具体比较如图9所示。

图6 Blood和Planning的聚类效果

图7 Parkinsons的聚类效果

图8 Vertebal的聚类效果

如图6、图7 所示，非独立分布下二次幂耦合的文献[4]、文献[20]、文献[17]中的方法在Blood、Planning、Parkinsons 数据集上，能够有效地降低聚类的平方误差和，这得益于非独立同分布的二次幂耦合的有效性，另外整体趋势从左往右依次减少，验证本文聚类迭代方法的有效性，说明了相对于最大距离积[20]的方法、文献[4]的方法，以及文献[17]中优化后的Min_max 选点方法，在非独立同分布下，本文算法聚类效果提高，另外迭代的次数如图9所示，本文方法在Blood、Parkinsons、Planning数据集上迭代的次数是最小的，即收敛的速度最快，说明了本文的Q-C-Kmeans算法在收敛性上的有效性。

如图8所示，本文的Q-C-Kmeans算法相比文献[4]、文献[20]、文献[17]中的方法在Vertebal数据集聚类效果不佳，出现这种情况的原因，在数据集相同的前提下，主要考虑到数据本身存在离群点的影响，因为本文的方法在处理完数据集后只是对于选点进行的优化，使得初始选点不会选到离群点，但是离群点依然存在，选点的不同会引起质心的位置不同，而误差和又是以簇中其他点与质心的整体差作为评价标准的，所以一旦簇中的离群点相对较多，质心与簇中其他点之间距离相对较大，可能会导致聚类的误差和变大，综合考虑是该数据集的本身离群点影响，虽然出现上述问题，如图9所示，但是在迭代次数上本文算法最小，收敛速度也是最快的，所以本文方法在多分类的数据集上也是有一定效果的。

在运行时间上比较如图10，由于本文的Q-C-Kmeans算法需要优先处理数据集，为了统一标准所以都是在非独立同分布下二次幂进行的比较，本文也是10 次取平均值，整体上在非独立同分布下，本文的Q-C-Kmeans算法的运行时间虽然略大于其他文献中的方法，但是相对来说合理，另外本文的Q-C-Kmeans 算法的运行时间跟初始中心选点个数、数据集的大小有一定的关系，本文所选的数据集的类别个数比较少，导致聚类迭代的次数比较少，数量上不是很大，所以运行时间相对来说合理。

图10 运行时间的比较

综合分析Q-C-Kmeans算法在二分类的Blood、Parkinsons、Planning的数据集效果比较好，在准确率、聚类效果，以及收敛速度上都是最佳的，考虑到由于离群点的影响，导致本文方法相比之前的算法在Vertebal 的三分类数据集上的聚类效果不佳，但是在收敛性以及准确性上本文方法有一定的优越性。整体上分析本文的QC-Kmeans算法是可行性的。

4 结束语

本文主要是针对于文献[17]的一种改进，针对文献[17]算法的最初选取中心点的随机性，以及在非噪声领域利用Min_max的方法，可能出现其他选点紧凑的情况，容易陷入局部最优，聚类不稳定，最终影响聚类效果，经过研究之后提出了二次幂耦合的K-means聚类算法研究（Q-C-Kmeans），相对于文献[17]，利用二次幂的思想可以将独立同分布下数据中隐含的信息更好地挖掘出来，本文又提出一种新的求解密度参数的方法，在最优高密度区域避免离群点的影响，同时提供聚类迭代的思想使得选点较远，克服文献[17]可能出现选点紧凑的问题，另外初始选取密度最大的点，很好地解决了文献[17]最初选取中心点的选点随机性问题，使得聚类稳定，实验表明，相比之前的研究有了新的进展，在二分类数据集的准确率上，聚类效果、收敛速度有很明显的提高，另外发现了多分类的数据集上可能会因为数据集的离群点的影响，引起聚类的效果不佳，但是整体上来说本文的Q-C-Kmeans算法还是有效的、可行的，另外本课题将会在混合型数据进一步研究，希望今后可以应用到相应的领域。