一种基于PLL的牵引电机速度辨识算法

鞠艳杰，黄石军，左运

(大连交通大学 电气信息工程学院，辽宁 大连 116028) *

交流电机作为工业控制领域的重要电气设备被广泛应用，电机传动系统是一个复杂的动力机械系统[1].轨道交通牵引传动系统中目前所采用的牵引电机是交流感应电机，同样，其是一个复杂的系统.传统牵引传动系统中检测电机转速所用的一般是机械式速度传感器，其容易受环境影响，需要经常维护[2].为了提升牵引传动系统的可靠性，牵引电机的无速度传感器控制技术越来越受到学者们的关注.对于电机的速度辨识算法，目前主流的研究方向有信号注入法[3]、模型参考自适应法[4-5]、全阶状态观测器[6-7]、扩展卡尔曼滤波器[8]以及滑模观测器[9-10].

近年来，基于锁相环(phase-locked loop，PLL)的速度辨识算法由于其易实现和优秀的性能成为新的研究热点[11-12]，但是PLL容易受到直流偏置、幅值突变等干扰的影响.本文提出一种基于PLL的速度辨识算法，在此算法中引入闭环转子磁链观测器和幅值归一化环节，弥补PLL本身在抗干扰能力上的不足.通过闭环转子磁链观测模型抑制了转子磁链中可能出现的直流偏置，引入幅值归一化环节抑制了可能出现的转子磁链幅值波动.最后通过仿真验证了算法的正确性和有效性.

1 基于PLL的速度辨识算法

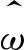
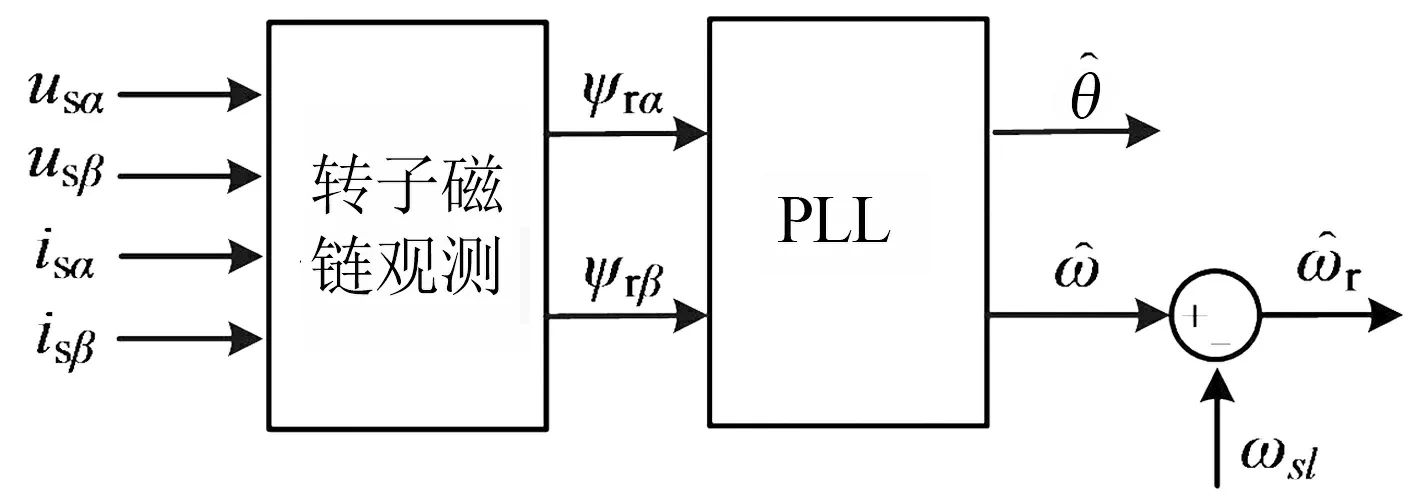
图1 基于PLL的速度辨识算法框图

传统的牵引电机在两相静止坐标系下定子磁链的电压模型：

(1)

式中：ψs=[ψsαψsβ]T，ψs为定子磁链矢量，us=[usαusβ]T，us为定子电压矢量，is=[isαisβ]T，is为定子电流矢量，Rs为定子电阻，T为矩阵转置符号. 利用感应电机在两相旋转坐标系下的数学模型，可以推导得到：

(2)

式中，Lm为互感，Tr为转子时间常数，isq为定子

2 PLL及其性能

图2中给出了PLL的框图，包含三部分：相位检测器(phase detector , PD)由d-q变换组成，环路滤波器(loop filter，LF)由比例积分(proportional integral，PI)组成，压控振荡器(voltage-controlled oscillator，VCO)由积分器组成.

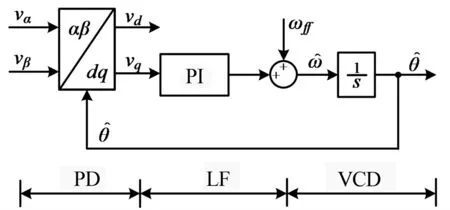
图2 PLL结构框图

为验证PLL的抗干扰性能，所做测试如图3、图4所示，从图中可以看出当输入信号出现直流偏置时，会使PLL的估计性能大大降低，同样当幅值突变时，对PLL的估计性能也会有所影响.

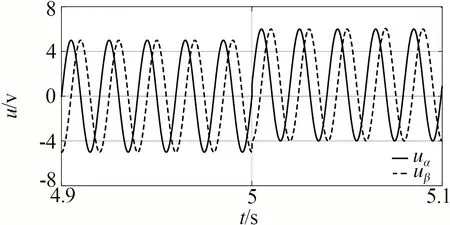
(a) 输入信号直流偏置突变

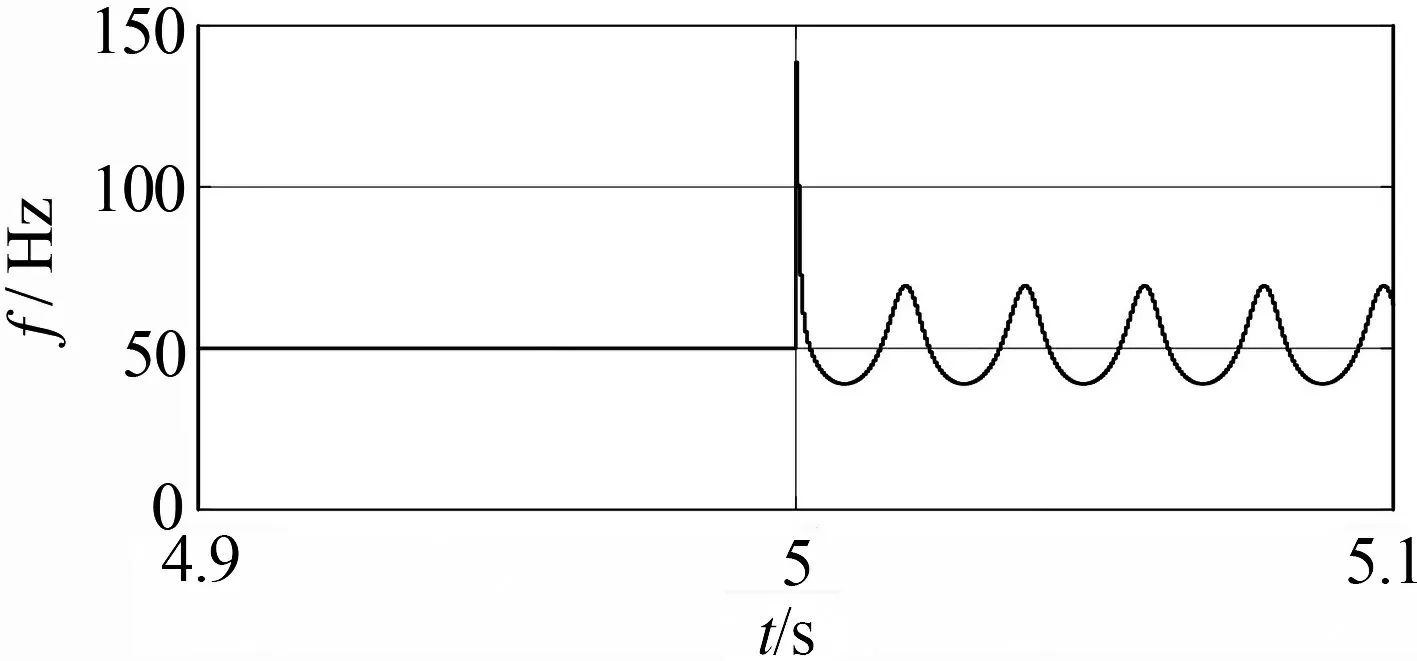
(b) 所测频率波形图3 PLL直流偏置影响测试

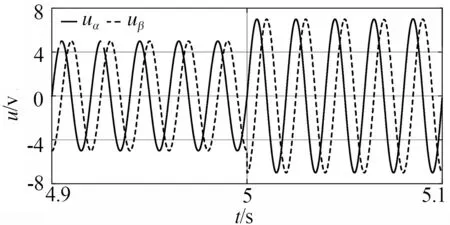
(a) 输入信号幅值突变

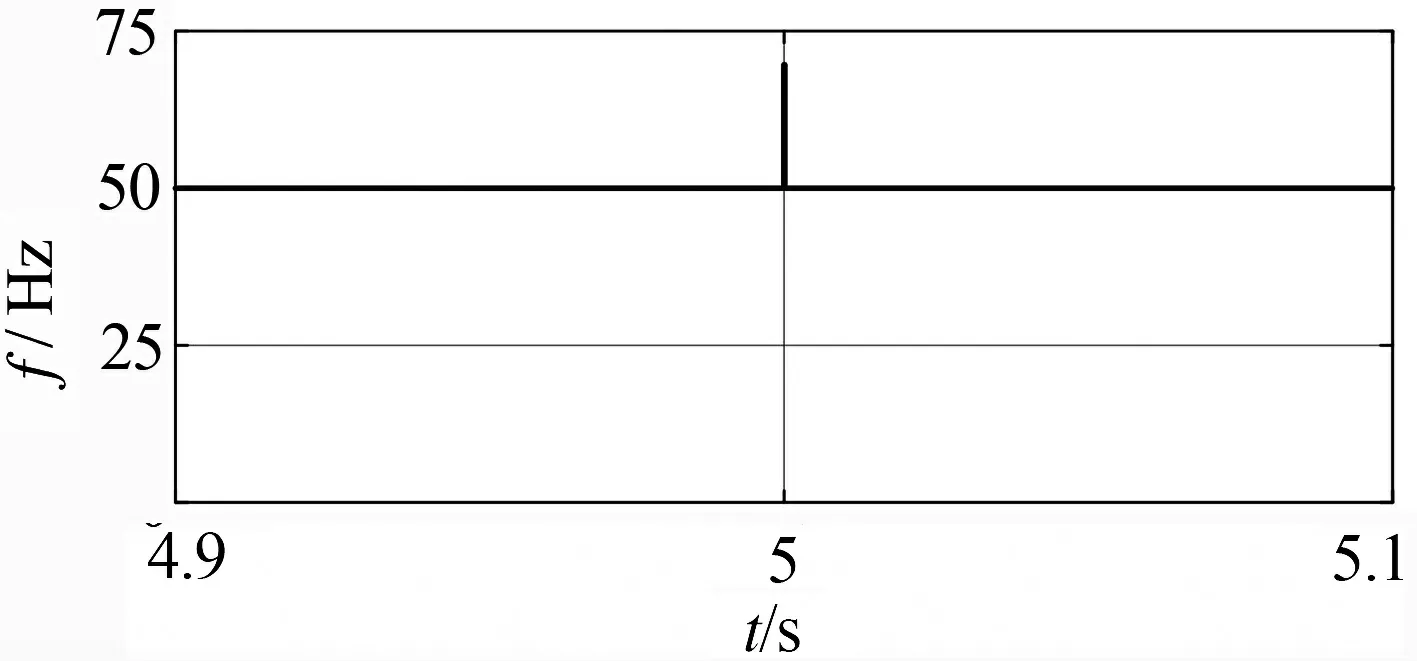
(b) 所测频率波形图4 PLL幅值突变影响测试

在实际中,由于电磁干扰、传感器测量和采样误差等会造成纯积分环节直流偏置和积分饱和的问题[13]，另外，由于牵引电机工况的复杂性，转子磁链幅值会经常变化，为降低可能出现的干扰影响PLL的估计性能，必须采取一些措施提升基于PLL的速度辨识算法的抗干扰性.

3 改进后的基于PLL的速度辨识算法

3.1 闭环转子磁链

电压模型的实际应用由于模型中对反电动势的纯积分环节易引起引起直流偏置，从而导致观测误差，对PLL的估计性能造成干扰.文献[14]提出一种闭环转子磁链模型，将电压电流模型相结合，解决传统电压型转子磁链模型的直流偏置问题.

当按转子磁链进行定向解耦时，牵引电机在两相旋转坐标系下的转子磁链的电流模型：

(3)

ψrq=0

(4)

式中，ψrq为转子磁链在q轴的分量，isd为定子电流在d轴的分量.为了补偿积分和定子电阻压降引起的误差，将定子磁链的电压模型修正为：

(5)

式中，Ucom为补偿量，可以通过比例积分调节器来实现：

(6)

式中，ψ′s为电流模型计算出的定子磁链，Kp、Ki为比例积分调节器增益.

根据感应电机在两相坐标系下的数学方程可以得到以下关系式[15]：

(7)

式中：ψr=[ψrαψrβ]T，ψr为转子磁链矢量，Ls为定子电感.闭环转子磁链观测框图如图5所示.

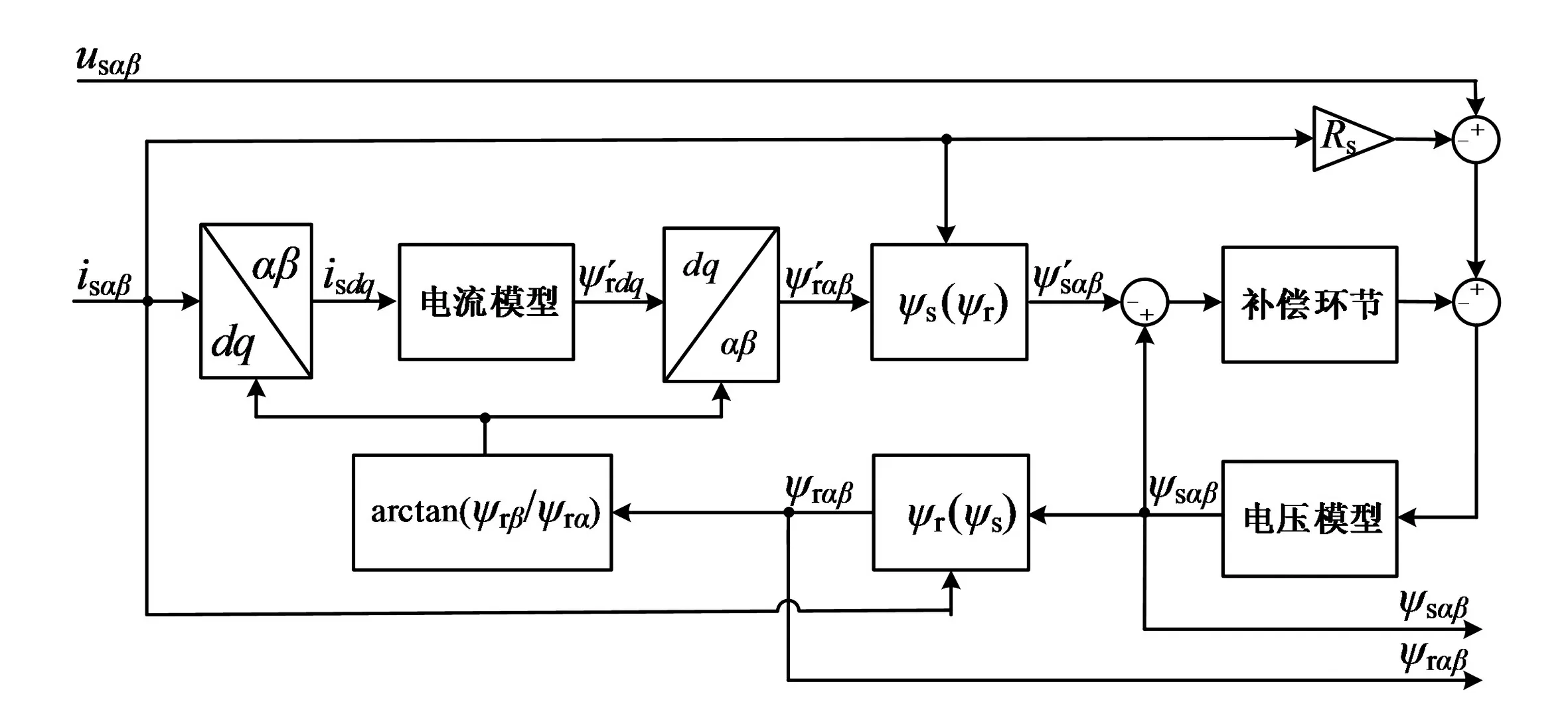
图5 闭环转子磁链观测框图

为验证闭环转子磁链的性能，所做测试如图6所示，通过在us中加入直流量观察不同的磁链模型的观测波形，从结果可以看出闭环转子磁链具有抑制直流偏置的性能.

(a) 闭环转子磁链模型观测波形

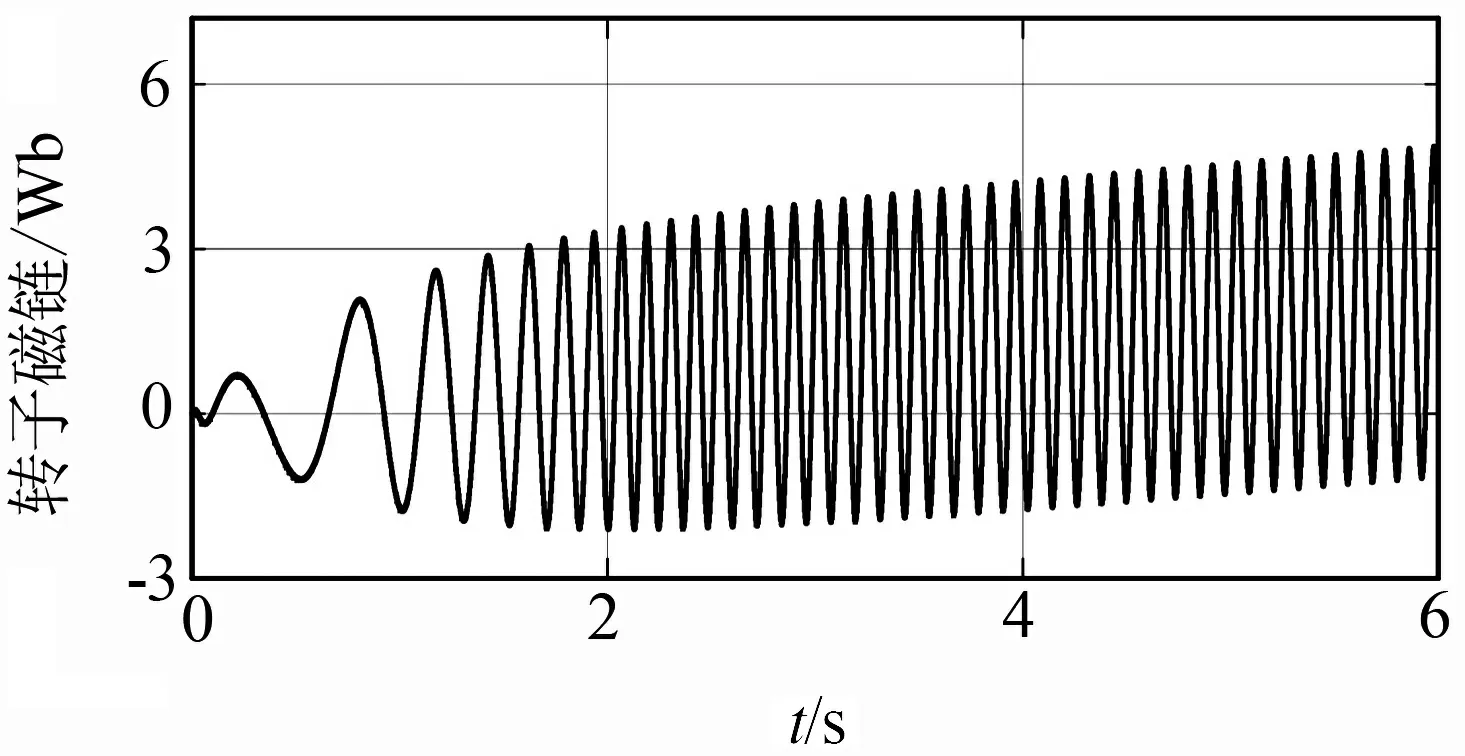
(b) 电压型转子磁链模型观测波形图6 不同转子磁链模型观测波形对比

3.2 幅值归一化

幅值归一化方案原理框图如图7所示，为抑制输入信号的幅值突变，有必要引入幅值归一化环节，未验证其性能， 所作测试如图8所示.从测试结果，可以看出当复制归一化环节有效地抑制了，输入信号幅值突变对PLL估计性能的影响.

图7 幅值归一化方案原理框图

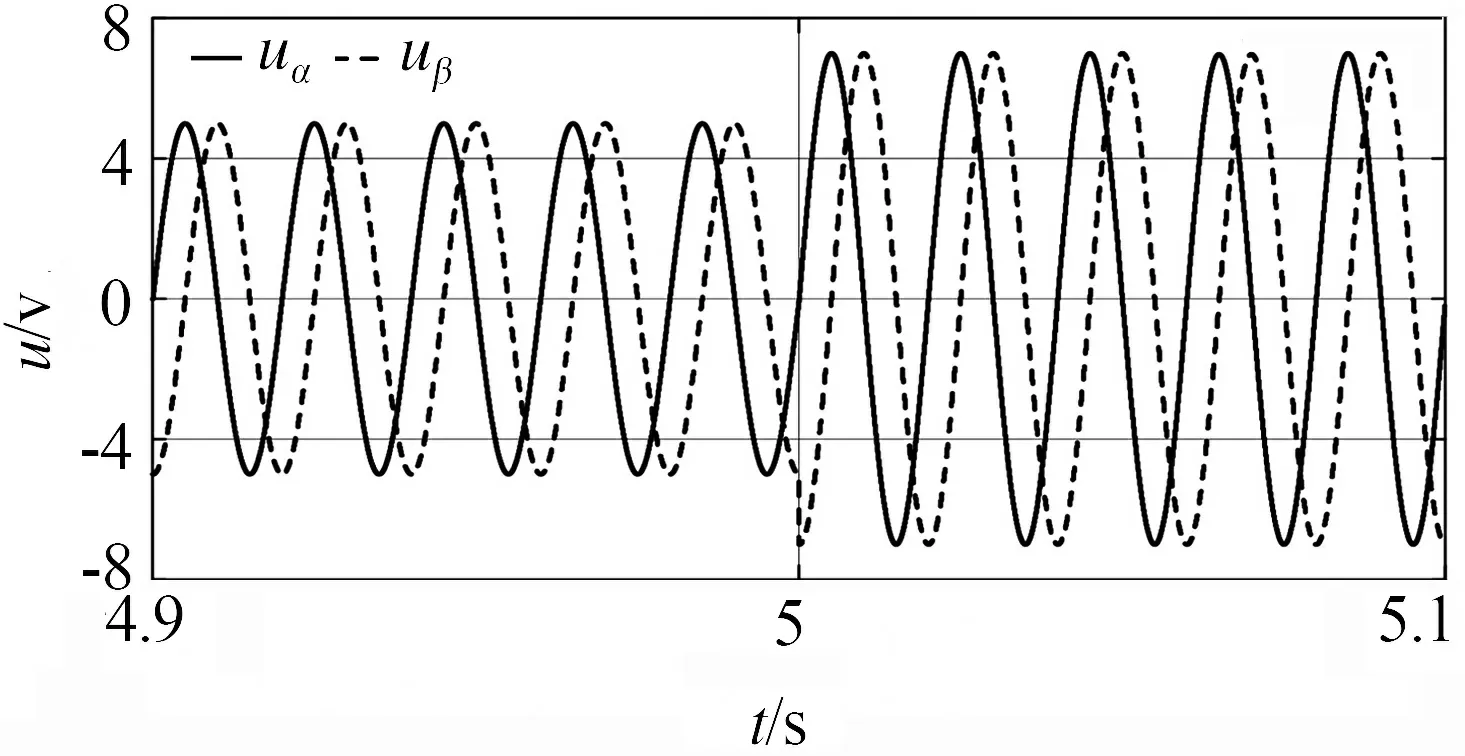
(a) 输入信号幅值突变

(b) 所测频率波形图8 引入幅值归一化后PLL幅值突变影响测试

3.3 改进后的基于PLL的速度辨识算法

在引入闭环转子磁链和幅值归一化环节后，得到改进后的基于PLL的速度辨识算法框图如图9所示.

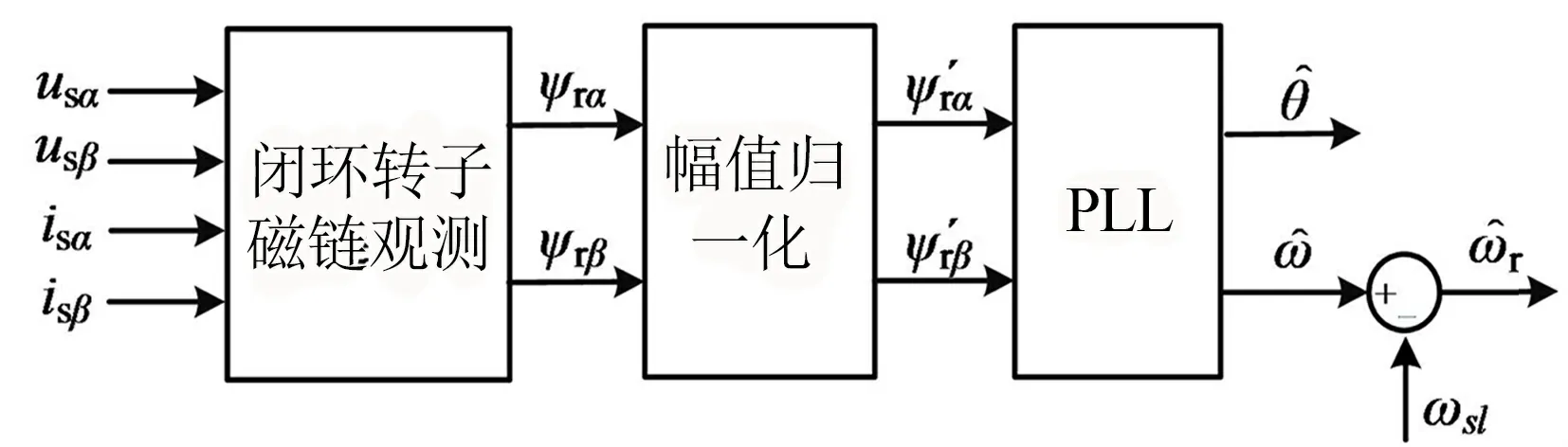
图9 改进后的基于PLL的速度辨识算法框图

4 仿真结果

为验证图9所示的速度辨识算法的性能，进行相应的仿真测试.选取的牵引电机参数：额定功率PN=562 kW，额定电压UN=2 700 V，额定电流IN=145 A，额定转速nN=4 100 r/min，定子电阻Rs=0.106 5 Ω，,转子电阻Rr=0.066 3 Ω，定子电感Ls=0.054 92 H，转子电感Lr=0.055 H,互感Lm=0.053 61 H.

为验证算法的性能，所设计工况变化：①在恒定负载转矩情况下，初始转速由n=500 r/min突增为n=1 000 r/min再突降为n=500 r/min; ②在恒定转速情况下，初始负载转矩由TL=100 N·m突增为TL=500 N·m再突降为TL=100 N·m.

仿真结果如图10、图11所示，可以看出稳态时，辨识转速误差很小，当电机在恒定负载转矩下，转速突变时，辨识转速能够很好地跟踪上实际转速，在恒定转速下，负载转矩突变时，辨识转速的波动较小，抗干扰能力较强.改进后的基于PLL的速度辨识算法具有较好的稳态及动态性能.

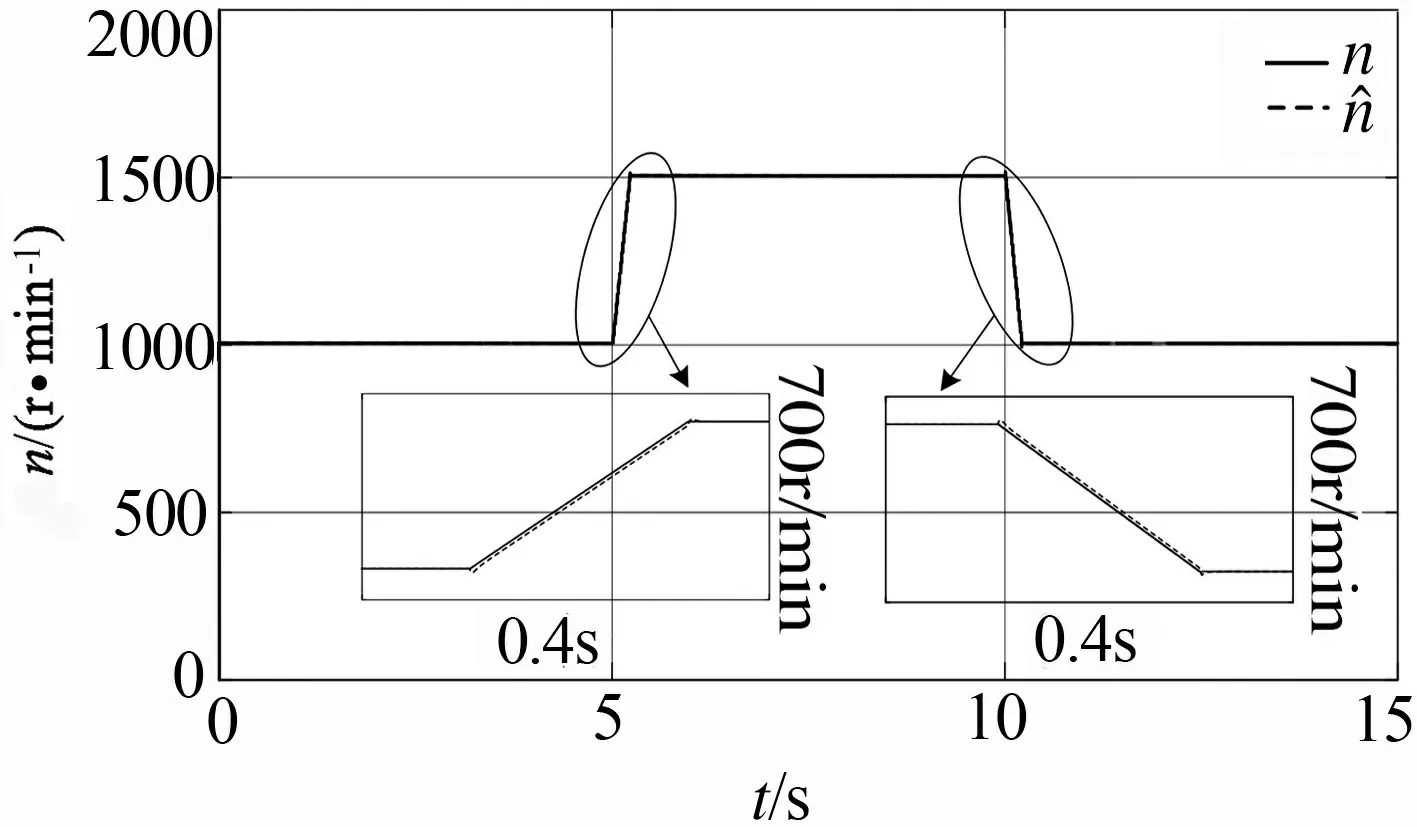
(a) 实际转速和辨识转速

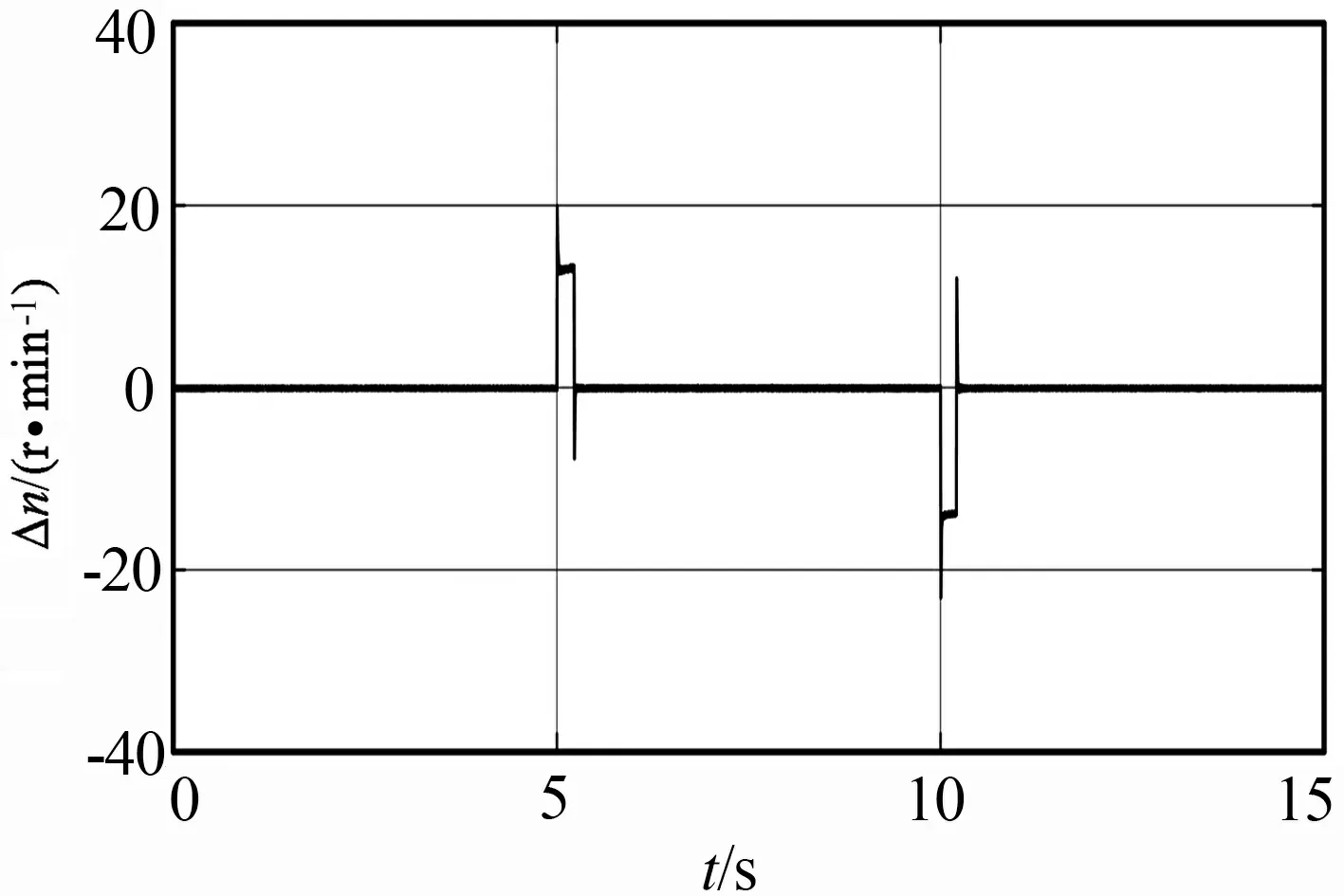
(b) 辨识转速误差图10 恒定负载转矩下，转速突变仿真结果

(a) 实际转速和辨识转速

(b) 辨识转速误差图11 恒定转速下，负载转矩突变仿真结果

5 结论

由于PLL本身有限的抗干扰性，本文在针对牵引传动系统中可能出现的干扰研究了解决办法，以提升基于PLL的速度辨识算法的抗干扰性能.通过闭环转子磁链模型观测转子磁链抑制了可能出现的直流偏置，引入幅值归一化环节抑制了可能出现的转子磁链幅值波动.最后，通过仿真验证了速度辨识算法在不同工况下的性能.