基于累积前景理论的物流配送干扰管理问题研究
2021-07-28张鹏石莎莎宁涛
张鹏,石莎莎,宁涛
(1.大连交通大学 创新创业教育学院, 辽宁 大连 116028;2.大连交通大学 软件学院,辽宁 大连 116054;3.大连民族大学 计算机科学与工程学院,辽宁 大连 116600) *
随着中国电子商务的普及,物流公司的分销需求逐年增加.然而,物流公司也面对许多干扰问题的发生,如配送车辆发生故障导致客户的送货时间延迟,客户的取消送货,以及客户的送货时间改变等因素.如何运筹好一个合理的物流配送方案, 保证客户的货物准时到达而不影响客户的满意度是物流公司需要解决的问题.
近年来,许多学者在车辆调度的干扰问题上取得了很大进展. Francesco Ferrucci[1]针对动态车辆问题,提出了一种新的主动实时控制方法,利用随机理论引导车辆进入未来可能的需求区域,来最大限度地减少客户的不便. Mu Q[2]针对车辆运输途中发生的故障,提出两种禁忌搜索算法,能快速生成新的方案,通过实验验证了算法的有效性.赵亮等[3],杨文超等[4]运用干扰管理思想,建立了干扰管理方案, 调整车辆的配送使干扰最小化.曹庆奎等[5]构建了客户价值的干扰管理模型,从整体上降低了客户的不满意度.符俊波等[6]将干扰管理思想应用在生活垃圾收运的车辆调度上,对收集点垃圾量的变化提出扰动恢复策略,有效地减少了车辆的成本.
前景理论和累积前景理论是由Kahneman和Tversky[7]提出,是决策者在面临风险条件时对结果的选择进行分析的理论.车辆的干扰问题也会面临着决策的风险,对此,学者们运用前景理论进行了研究.YANG L[8]提出了累积前景理论方法来解决应急响应中的风险决策问题.任斌等[9]对灾后应急救援物资的动态变化,建立了价值函数和概率权值, 通过求得前景值最小得到救援方案,提高了救援的效率.通过前景理论,宁涛等[10]从用户对货物期待送达时间角度,建立了用户心理期望感知函数模型.Diana L[11]研究了时间压力对决策行为的影响,并建立了相应的风险承担模型,实验验证了时间压力下增加了风险寻求收益.黄婷婷等[12]对不同年龄段的乘客出行的路径选择进行了研究,通过前景理论描述了乘客对路径选择上的决策行为.
基于干扰管理思想,本文提出一种干扰策略,并建立了扰动恢复模型.同时,考虑干扰后对客户满意度的影响,将累积前景理论与干扰策略相结合.改进的蚁群算法旨在解决这个问题,最后通过数据的测试验证了算法和干扰策略的有效性.
1 基于累积前景理论
1.1 累积前景理论描述
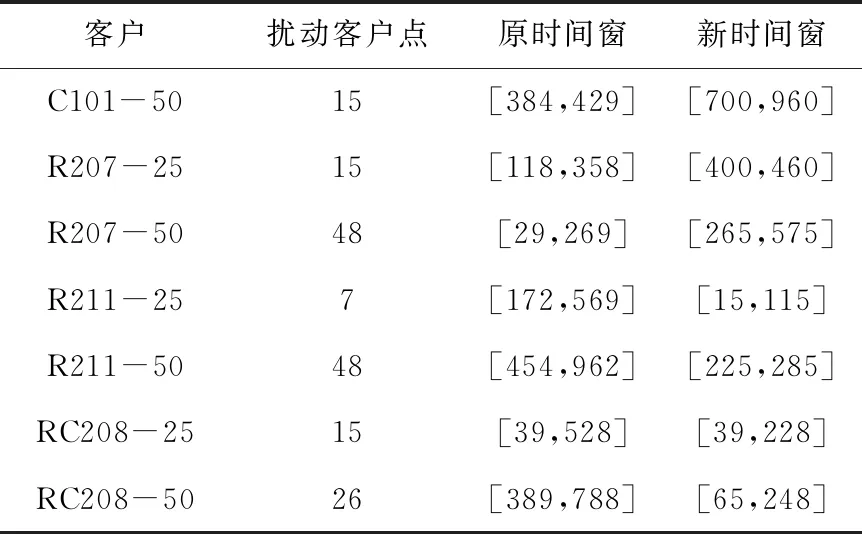
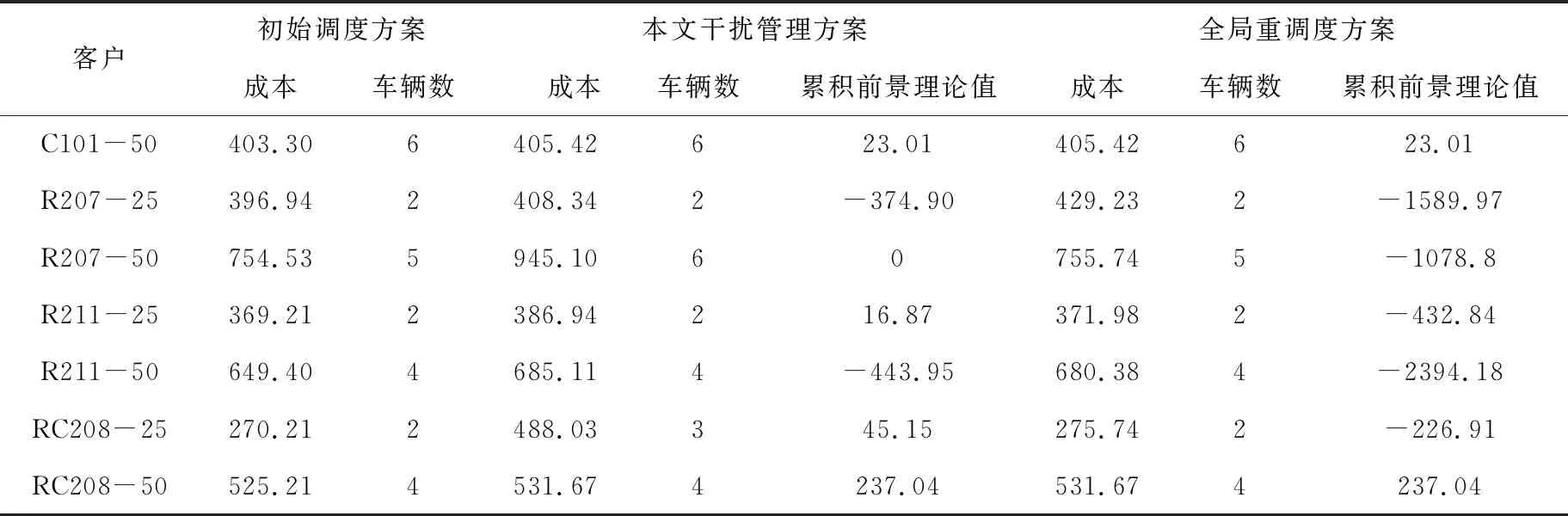
对于物流商而言,客户的满意度直接影响到物流商的信誉度.物流商希望最大可能的在客户规定的时间窗[ETi,LTi]内送到货物,同时也希望能增加客户i的满意度.根据前景理论,由于配送货物到达时间是不确定的,客户i会通过某种渠道获取配送到达时间T0,i(即在不发生干扰情况下,初始调度送达时间)作为心理预期的参考点,如果实际配送到达时间Th,i在[ETi,LTi]内,并且到达时间Th,i 本文选择初始调度方案客户i预期到达时间T0,i作为参考点,与干扰发生后实际配送时间Th,i作比较,xi=T0,i-Th,i表示客户预期到达时间与实际到达时间的差值,xi≥ 0, 表现为收益;xi<0, 表现为损失.对于干扰的客户,干扰发生后,客户i的心里预期的参考点也会随之改变,参考点变成调整方案后获取新的配送到达时间;对于无法配送而取消的客户i实际配送时间变成0,即Th,i=0, 心里预期的参考点变成客户i的服务时间窗下限LTi, 这样增加损失程度,加大取消客户的惩罚;对于新增车辆上客户的价值函数v(xi)=0. 价值函数公式(1)如下: (1) α和β表示风险偏好系数,分别表示在收益与损失价值函数的凹凸程度,λ表示损失规避系数,λ越大,代表客户的不满意度增加;反之,减少.本文参照研究数据,a=b=0.88,λ=2.55. 在干扰发生后,每个客户对货物配送是否提前或者晚到的心理预期存在一定的概率p,对于取消的客户心里预期概率p=1,pi公式如下: (2) (3) (4) 式中,[ETi,LTi]代表客户的时间窗,xi≥0,表示“收益”,收益权重为ω+(p)如式(3),xi<0,表示“损失”,收益权重为ω-(p),如式(4).本文参d照研究数据,З=0.61,δ=0.69. 累积前景理论模型是将单个的概率事件整合在一起,从全局的角度进行前景理论分析,因此本文建立了相关的模型. 单个客户的前景值U(xi),其中,v(xi)+表示“收益”,v(xi)-表示“损失”.公式为: U(xi)=v(xi)-ω-(p)+v(xi)+ω+(p) (5) 累积前景值f1,公式为: (6) 单个客户前景值是每个客户收益值值与损失值之和,累积前景值f1是所有用户前景值之和.在干扰发生后,物流商调整方案,通过计算累积前景值f1,来判断是否对客户满意度干扰较大.当f1≥0,说明干扰后的方案增加了客户的满意度,f1越大,客户满意度越高;当f1<0,说明干扰后的方案降低了客户的满意度,f1越小,客户满意度越低. 其中,V′为干扰发生时未完成的客户集合;P为初始方案的路径集合,P′为新方案的路径集合; P′={(i,j,k)|∀i,j∈V',k∈K} (7) 物流商希望干扰后的总成本f3最小化.在成本上分为3种,第1种是增派车辆产生的成本C1;第2种是车辆的运输成本Cij;第3种是取消客户产生的成本C2.其中,n1为增派车辆数量,n2为取消客户数量. (8) 干扰管理可以描述为: 配送中心得到满意的初始调度方案后, 发生信息的干扰(客户的增加、时间窗和货物的变化等), 配送中心需要在满足客户的时间和需求下, 调整初始方案,使其变动造成的干扰最小化. 变量和符合定义如下: V:V={v0,v1,…,vN}其中,v0为配送中心, {v1,v2,…,vN}为客户点集合;V′为干扰发生时未完成的客户集合;dij为客户i到客户j的距离;K:K={1,2,…,k}表示所有配送车辆集合;tij为两点i和j之间的行驶时间;Si为客户i的开始服务时间;si为客户i的服务时间;wi为客户i的等待时间;ETi为客户i的时间窗下限;LTi为客户i的时间窗上限;ETi′为客户i的新时间窗下限;LTi′为客户i的新时间窗上限;G为车辆的载重量;Gk为干扰发生时车辆k的载重量;gi为客户i的需求量. 本文的目标函数用字典排序[13]表示.目标第一优先级P1是对客户服务时间的累积前景理论值偏离最小; 目标第二优先级P2是对车辆路径的偏离最小; 目标第三优先级P3是对物流商成本的花费最小. 目标函数: Min LexP1∶f1P2∶f2P3∶f3 (9) P1≫P2≫P3 决策变量: 约束条件: (10) (11) (12) (13) (14) Si=tij+wi,∀i,j∈V (15) Siyik≥ETi,∀k∈K,∀i∈V (16) Siyik+si≤LTi,∀k∈K,∀i∈V (17) Siyik≥ETi′,∀k∈K,∀i∈V (18) Siyik+si≤LTi′,∀k∈K,∀i∈V (19) 在该数学模型中,式(10)表示配送车辆服务的客户点的总体需求量不大于车辆载重限制; 式(11)表示干扰发生后配送车辆服务的剩余客户点的总体需求量不大于车辆载重限制;式(12)表示干扰发生后临近救援车辆服务的客户点的总体需求量不大于车辆载重限制; 式(13)表示所有车辆从配送中心出发,必须返回配送中心; 式(14)表示客户只能被一辆车服务,或者取消服务; 式(15)~(19)表示时间窗约束. (1)增派车辆策略 当调整后的方案对初始方案干扰较大,或者不能按时配送,选择增派车辆配送,但增派车辆配送会增加车辆的成本. (2)临近救援策略 利用现有的在途车辆进行的局部调整策略, 需要考虑客户的时间和车辆的容量要求, 是否能满足干扰发生时的情况. (3)取消客户策略 不能满足前两个策略,或者车场没有多余车辆进行配送,对客户改日配送. 蚁群算法具有的较强的鲁棒性和易于其他算法相结合等优点,能很好的解决调度方面的相关问题,但单独的蚁群算法在研究复杂问题时容易陷入局部最优、收敛速度慢以及搜索最优路径时间过长等缺点[14]. 针对该缺点,本文提出自适应蚁群算法,在改进转移概率和信息素更新方式的同时,引入模拟退火算法[15],加快了算法的收敛速度. (20) 其中,τij是从i到j的信息浓度,α为信息素浓度的重要因子,ηij为启发函数,ηij=1/dij,表示蚂蚁从客户点i到j的期望程度,β为启发函数的重要程度因子,φij是时间启发函数,φij=(LTj-ETj)/lj,其中[ETj,LTj]为客户j时间窗,у为客户的时间程度因子,ωij是路径启发函数,ωij=(di0+dj0)/dij,di0是客户i到车场的距离,dj0是客户j到车场的距离,θ为路径的程度因子,allowk表示车辆在满足条件下可访问点的集合. 蚁群算法寻优的快速性是通过正反馈的信息传递和积累来保证的,为了充分利用循环找到最优解,在每次循环后,对一只蚂蚁的信息素进行更新.本文提出自适应蚁群算法改进更新策略,更新规则如下: (21) 其中,φ(m)=m/c为一个与迭代次数m成正比的函数,迭代次数越大φ(m)的取值越大,c为常数.在蚁群算法中,蚂蚁通过转移概率选择下一个转移的目标,所以参数的设置会对算法的收敛速度和求解质量上产生很大的影响.因此,本文引入了模拟退火的机制,并动态的调整参数,有效地帮助算法跳出局部最优解. 步骤如下: 参数含义:Hk+1为当前蚂蚁完成循环后得到的局部最优解,Hk为上一次循环后得到的局部最优解,NC代表循环次数,T为当前温度,按照模拟退火机制,每次迭代之后进行降温,TNC+1=TNC·r,r为降温速率. (1)当循环NC> 1时,ΔH=Hk+1-Hk,如果ΔH< 0 ,则保留当前最优解Hk+1.证明得到的解优于上一解,并保留当前的参数ɑ、β、у. (2)如果ΔH= 0;或者p=exp(-ΔH/T),如果p是(0,1)之间的随机数,则接受新的恶化解作为最优解.此时说明算法可能陷入局部最优解,信息素浓度过高,期望值太大,需要减小α,增大Ω, 其中,(β、у、θ)∈Ω. (22) (3)如果ΔH> 0,并不能接受恶化解,则最优解为Hk.此时,反应出信息素对蚂蚁选择路径的影响力较小,需要增大α,减小Ω. (23) 步骤1:生成初始调度方案,根据改进的蚁群算法以成本最小为目标求解. 步骤2:当干扰发生时刻,客户的时间窗发生变化.首先有必要判断变化是否会干扰初始方案.本文采用文献[16]提出的方法来判别是否需要改动初始方案.客户i的原时间窗为[ETi,LTi],对客户i的服务时间为Si,变动后客户i的新时间窗为[ETi′,LTi′] ,tmin={LTi-Si}表示客户i当前所在的车辆路径上后续客户j的时间窗上限与开始服务时间的最小差值.所以,满足客户i需要变动初始方案的条件为:LTi′ 步骤3:在发生干扰后,排除已服务的客户,并且以当前车辆位置为虚拟配送中心,使用步骤1对当前车辆的剩余客户进行重新配送,并要求最后返回原配送中心.如果新方案无法配送或者对初始方案干扰较大,转步骤4; 步骤4:对干扰客户i进行新增车辆配送,或者取消配送. 本文选取文献[16]的数据进行测试,假设条件:一个配送中心拥有8辆汽车,每辆车载重为5吨,车速为1单位,单位运输成本为1,增派车辆成本为140,取消客户的成本为240.表1包含了配送中心和客户的信息,其中0代表配送中心,1-15代表客户. 表1 客户信息表 改进的蚁群算法参数设置:蚂蚁数目为30,迭代次数为NC=200,信息素总量Q=100,α=1,β=3,у=3,θ=3,ρ=0.1,T=1 000,r=0.9,c=5. 采用本文改进的蚁群算法得到最优的初始方案:车辆1:0-9-7-6-0;车辆2:0-10-5-13-0;车辆3:0-8-4-15-14-12-0;车辆4:0-3-11-2-1-0.得到的成本为526.30,优于文献[16]的531.41. 当时间为32.65,客户4、6、13、14信息发生变动,变动信息如表2. 表2 客户时间窗变动信息 配送中心收到干扰信息,首先,查看当前车辆所在的位置,并查看此车辆是否存在干扰客户.若不存在,正常配送;若存在,按照本文提出的干扰策略,进行调整.调整后的方案为:车辆1:0-9-7-6-0;车辆2:0-10-5--0,客户点13,需增派车辆5进行配送;车辆5:0-13-0;车辆3:0-4-8-15-14-12-0;车辆4:0-3-11-2-1-0. 本文针对干扰发生时刻客户时间的改变,应用在按原计划调度和全局重新调度上,来验证提出的干扰方案的效果. 按原计划调度方案:车辆1:0-9-7-6-0;车辆2:0-10-5-0,客户点13,需增派车辆5进行配送;车辆5:0-13-0;车辆3:0-8-15-14-12-0,客户4无法进行配送,取消客户4的配送;车辆4:0-3-11-2-1-0. 全局重新调度方案:车辆1:0-10-5-0;车辆2:0-6-0;车辆3:0-13-9-7-0;车辆4:0-3-11-2-1-0;车辆5:0-4-8-15-14-12-0. 三种配送方案的结果如表3所示. 表3 三种方案的结果比较 从表3可以看出,本文提出的干扰管理方案累积前景值明显优于原计划配送和全局重调度方案;干扰管理方案的路径偏离与原计划配送方案的路径偏离相差不大,优于全局重调度方案的路径偏离;干扰管理方案成本高于全局重调度方案成本,但明显低于原计划配送方案成本. 由此可见,本文提出的干扰管理方案相对于其他方案对于客户的满意度干扰较小,甚至提高了客户满意度,这增加了客户对物流的信任度.虽然在成本和路径偏离上不优于其他方案,但相差不大.这说明本文提出的干扰管理方案的有效性. 补充说明,对于文献[16]提出的初始调度方案,针对干扰客户6,需要重新增派车辆进行配送,若采用本文的初始调度方案,干扰客户6无需增派车辆,这就大大减少了干扰,说明初始调度的好坏,对干扰管理也产生很大的影响. 为进一步验证本文提出的干扰管理方法有效性,本文采用Solomon标准测试算例[17]进行验证,选取C101的前50个客户、R207、R211和RC208中数据的前25个客户和前50个客户.假设T=50时刻,客户配送要求时间发生变动,变动信息如表4. 表4 各组客户的时间变动信息 本文将选取的算例的干扰管理与全局重调度方案进行了比较,结果如表5所示. 表5 干扰管理与全局重调度方案结果的比较 由表5可以看出,本文选取的C类C101-50和RC类RC208-50数据的干扰管理方案和全局重调度方案相同,这是由于客户的分布是聚集的,聚成多个区域,区域之间跨度较大,车辆间无法协助.相反, R类客户是分散的,干扰后对全局重调度影响较大.而RC208-25中由于干扰客户对干扰方案扰动较大,采用重新安排车辆策略. 由此可见,C类和RC类客户是集群分布,配送车辆间的协助策略无法实施,存在干扰管理方案和全局重调度相同情况,而R类问题本文干扰管理方案效果会更加明显.在成本上,干扰管理方案的成本总体上高于全局重调度方案成本,但部分相差不大且R207-25中干扰管理方案成本低于全局重调度成本.在累积前景理论值上,干扰管理方案的累积前景值大于或者等于全局重调度的累积前景值,这证明了本文的干扰策略有效性,且部分累积前景值为正数,表明干扰后的方案提高了客户的满意度. 同时,本文的初始调度与Solomon标准数据上的最优解相差不大,其中在R207-25车辆数2,低于Solomon的3辆,这减少了运输的成本.在运行效率上,本文算法运行20次,在客户数量为25的平均时间为2.55 s,运行客户数量为50的平均时间为7.05 s.这证明了本文的算法有效性. 本文针对物流配送中客户时间发生改变的情况下,从客户满意度的角度出发,将累积前景理论运用在干扰策略上,同时考虑成本和路径偏离的干扰,以干扰管理最小化为目标,构建了字典排序方法和扰动恢复模型.最后,通过Solomon算例和文献的对比,验证了本文提出的干扰策略和算法的有效性.不足之处,本文只考虑了客户时间上的变化和单一的干扰时刻,对客户的需求和多个干扰时刻的带来的影响,未来需进一步验证.1.2 价值函数的确定
1.3 决策权重的确定
1.4 累积前景值模型

2 扰动恢复模型的建立及干扰策略
2.1 扰动恢复模型的建立
2.2 干扰策略
3 改进的蚁群算法的设计和步骤
3.1 改进的蚁群算法
3.2 改进转移概率
3.3 信息素更新策略
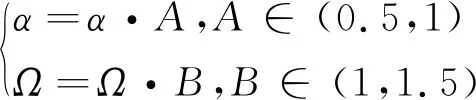
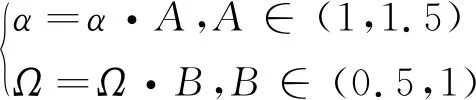
3.4 算法流程
4 仿真实验



5 结论
