一种基于ADPSO优化的循环神经网络模型

宋旭东,梁师齐,王雪梅

(1.大连交通大学 软件学院，辽宁 大连 116028；2.阜新高等专科学校，辽宁 阜新 123000) *

循环神经网络是一种深度学习模型，RNN内部的隐含层神经元节点之间相互连接，使其具有强大的序列建模功能，是一种处理股票价格、机票价格、风电功率等时间序列数据的理想模型，传统RNN存在收敛速度慢、易于陷入局部最优的问题.当前针对RNN的研究主要分为两类：①对RNN网络自身结构的改进增强；②RNN的参数优化.

根据以往的研究，RNN的参数优化研究虽在一定程度上克服了RNN存在的问题，但是由于优化算法自身存在一定缺陷，使得RNN的优化还有很大的进步空间.为此本文在现有研究[1-10]的基础上，提出了一种自适应调整的动态粒子群优化算法(ADPSO)，然后构建基于ADPSO优化的RNN模型.

1 相关方法介绍

1.1 粒子群算法

1995年，Eberhart和Kennedy提出了粒子群优化算法(PSO).对于种群粒子，主要根据式(1)、(2)对自身位置、速度进行实时调整，一直到符合收敛终止条件为止.

(1)

(2)

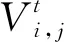
1.2 循环神经网络RNN

在常规RNN中将一个输入层序列、隐含层的矢量序列和输出层矢量序列分别用X、H和Y表示，输入层序列X=(x1，x2,…,xT)，隐含层序列H=(h1，h2,…,hT),输出层序列Y=(y1，y2,…,yT).RNN的训练公式如下：

ht=σsig(Wxhxt+Whhht-1+bh)

(3)

yt=Whyht+by

(4)

其中，Wxh、Whh、Why分别为输入层节点与隐含层节点、隐含层节点与隐含层节点、隐含层节点与输出层节点之间的权重矩阵；xt为t时刻的输入数据；ht是t时刻的隐含层节点状态；bh、by是常数.σsig是sigmoid，激活函数，用来激活控制门.sigmoid函数的表达式为：

(5)

2 自适应调整的动态粒子群算法

粒子群算法在具体应用过程中，存在着收敛速度过快、容易陷入局部最优值的问题.本文基于此提出了一种能够自适应调整参数的动态粒子群算法(ADPSO).

(1)动态粒子群算法

(6)

其中，t表示粒子当前的迭代次数，tmax是允许的最大迭代次数.

由式(6)知，随着t的增大，ln(e+t/tmax-1)也在增大，但其值始终不会大于1，导致式(6)中粒子的位置的变化速度变慢，并且式(6)中对数函数的引入使得每个粒子的位置获得了振荡，达到了动态地调整粒子的搜索空间的目的.

(2)动态粒子群算法中参数的自适应调整

①随机惯性权值的设置

为使算法有更好的搜索能力，应该控制算法的搜索状态，使其在前期的时候搜索能力较强，增加其搜索的速度，后期时应该精细地选择，增加其搜索的精度.所以惯性权值采用下式：

(7)

其中，ωstart、ωend分别表示惯性权值初始值和终止值，t、tmax与式(6)中含义相同.

根据式(1)、式(7)式可知，粒子群迭代前期，w较大，便于快速地展开搜寻，而在搜索后期，w较小，粒子群可以更仔细地搜索，利于其寻找最优.

②自动调节的学习因子

如果采用固定的学习因子，就容易使粒子陷入局部极值而跳不出来，因此引入一种自动调节的学习因子，具体调整方式为：

(8)

(9)

其中，cstart分别表示学习因子c1，c2的初始值，cend分别表示学习因子c1，c2的终止值，v=-ω，ω为式(7)中的惯性权值.

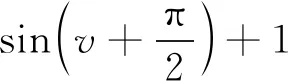
3 基于ADPSO优化的RNN模型

该算法的主要思想是通过ADPSO算法优化RNN的连接权值和阈值，改善RNN的性能.

ADPSO优化的RNN模型的具体步骤如下：

Step1：通过恰当的方式对粒子群、RNN参数进行初始化，粒子群参数包括迭代次数、种群规模、学习因子等.RNN参数主要包含隐含层的层数、神经网络各层的神经元个数.

Step2：对种群中各粒子的适应度值进行运算，式(10)表示粒子的适应度函数：

(10)

式中，n表示种群规模，Yi为神经网络实验数据样本预测值，yi为数据样本实际值.

Step3：计算每个粒子的适应度值.

Step4：根据式(7)对粒子惯性权值进行调节，然后参照式(8)、(9)对粒子的学习因子进行适当调整，同时，根据式(1)、(6)对粒子位置、粒子速度进行及时更新.

Step5：若迭代结束条件完全满足，那么模型训练将会立即结束，反之，将会自动跳转至Step2，再次进行迭代.

4 实验对比分析

为了更全面、更深入的对ADPSO、ADPSO-RNN模型进行验证，本文进行以下两个仿真实验：

(1)把ADPSO、PSO两种算法对基准函数Ackley、Griewank分别进行优化，然后对优化结果进行深入对比与分析；

(2)以某股票收盘价格历史数据为实验数据，将ADPSO-RNN与RNN、PSO优化的RNN分别对其进行预测，通过预测结果的对比验证其性能.

4.1 ADPSO算法性能测试

为证明ADPSO算法的性能，将ADPSO与标准粒子群算法(PSO)、在经典测试函数Ackley和Griewank上进行精度、维度、收敛速度的对比试验.

根据实验需要，对相关参数进行合理化设定，具体为：测试函数Ackley的解空间为[-32,32]，最小值mmin=0；测试函数Griewank的解空间为[-600,600]，最小值为mmin=0；群体规模为40；在PSO中，惯性因子、学习因子分别为2.0、1.5；在ADPSO之中，惯性因子从2.5非线性减到0.5，cstart=2，cend=0.5；对于三种算法而言，最大迭代次数完全相同，均为1000；维度均依次设为5、20、40.

由于测试结果精度非常高，并且不同优化方法的稳定值都会在数量级(这里的数量级取10-1为一级)内大范围变化，所以本本文采用数量级评价准则.公式如下：

value=-log10f(x)

(11)

其中f(x)为测试函数函数值.在这里value就可以直观表示测试函数的精度，value值越大，说明测试函数的精度越高.

表1为两种算法在不同维度下对Ackley和Griewank的优化结果.从表中可以得知，无论维度如何，ADPSO算法的优化结果相对于PSO而言均为最优.

图1为PSO算法与ADPSO算法分别在5维、20维、40维时优化Ackley函数过程中的适应度值曲线图.分析可知，越低维度所达到精度越高，但在越高维达到稳定值所用的迭代次数越少.

图2为两种优化算法在三种维度下优化Griewank函数过程中的适应度值曲线图，在ADPSO优化过程中发现了一个有趣的现象，即在高维的情况下对函数优化结果反而精确.这说明ADPSO算法在某种场景下更适合维度更高的情况.

表1 函数优化结果

(a) PSO算法 (b) ADPSO算法图1 函数Ackley图像及适应度值进化曲线

(a) PSO算法 (b) ADPSO算法图2 函数Griewank图像及适应度值进化曲线

4.2 股票价格预测

(1)实验数据

本章对浦发银行股票从2013年1月4日～2019年3月14日的股票价格数据进行实验，实验取的是根据当日股票收盘价作为该日的成交价格，实验数据总计1481组.本文的实验目的是用前1200组的股票成交价格数据来预测后续281组股票价 格 数 据， 故 在 实 验中将该路段前1 200组数据作为训练样本，后281组数据为检测样本.

图3 股票价格变化曲线

图3给出了实验数据.

(2)评价指标

在进行仿真实验的过程中，本文利用RNN、基于PSO优化的RNN与基于ADPSO优化的RNN分别进行股票价格预测，并将预测效果进行对比.输出三组预测实验结果，利用评价指标进行数据分析.对于预测结果的指标选取如下：

(12)

(13)

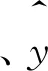
(3)预测结果对比分析

图4为三种算法预测结果对比曲线.表2为三种算法的预测误差结果对比统计.从中可以看出：基于ADPSO优化的RNN在预测指标MAPE及MSE上相对于RNN降低了6.014%和33.1867，相对于基于PSO优化的RNN降低了1.895 4%和6.625 1，预测结果的准确性得到明显提高；这主要是因为ADPSO算法相对于PSO在进行参数寻优的时候具有更好的寻优性能和搜索效率，能够更快、更好的找到最优结果，使得RNN在进行股票价格预测时具有更高的预测精度、预测效率及泛化性能.

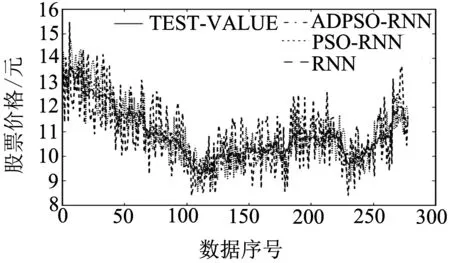
图4 三种算法预测结果对比曲线

表2 预测误差结果对比

5 结论

本文首先提出了一种PSO改进算法—ADPSO，该算法使PSO全局寻优能力、收敛速度得到提高；然后将ADPSO用于RNN初始权值和阈值参数的优化，构建基于ADPSO优化的RNN模型，该模型克服了传统RNN参数选取不精确的缺点，提升RNN的泛化性能.在实验中，一方面分别将ADPSO与PSO对基准测试函数进行优化，结果表明ADPSO具有较好的优化性能；另一方面将ADPSO-RNN与RNN、PSO-RNN模型分别对某股票数据进行预测，通过对比可以看出，基于ADPSO-RNN模型在对股票价格进行预测时能够更好的进行数据拟合.