基于压缩感知的图像混沌加密算法
2021-07-28张小康曾国辉
张小康,曾国辉
(广东工业大学 自动化学院,广东 广州 510006)
混沌系统是一种非线性系统,具有对初始值和参数极其敏感、遍历性以及伪随机性等属性。这些特性与密码学紧密相连,且满足密码学的基本要求,常用于图像加密领域[1]。但是,图像加密算法设计不仅要考虑算法的安全性和抗攻击性,还要考虑算法的计算量和算法实现的复杂度,要考虑算法的资源代价和计算时间代价。
压缩感知理论实现了信号从低维测量输出来重构高维稀疏输入信号,其信号在采集过程中实现了压缩,可以应用于自然图像这样的稀疏信号的存储与传输[2]。压缩采样过程可看成是加密过程,而测量矩阵就是密钥。该方法已经被证实具其密钥空间足够大,具有计算安全性,可以有效地抵抗暴力统计攻击[3]。由于压缩感知理论在图像处理过程中是一种线性压缩,不能很好地抵抗已知明文攻击和选择明文攻击,具有安全漏洞[4]。因此,为保证图像在传输过程中的安全性,将压缩感知理论和混沌理论相结合应用于图像加密过程中,可以有效地解决图像在存储和传输过程中的安全性能及压缩性能。
1 相关理论
1.1 压缩感知(CS)
压缩感知理论实现信号从低维测量输出来重构高维稀疏输入信号,其信号在采集过程中实现了压缩。过程如下:
假设长度为N的一维实离散信号X∈RN,可以采用N×N维正交基矩阵φ=[φ1,φ2,…,φN]的线性组合表示为:
x=Ψα
(1)
其中,Ψ为正交基矩阵,目的是将输入信号进行稀疏化处理,α为加权系数,能够对信号x进行压缩感知的前提条件是x具有系数性。
CS的测量过程表示为:y=Φx=ΦΨα=θa,该过程为降维过程,其中Φ为测量矩阵,θ为传感矩阵,压缩感知理论要求传感矩阵满足RIT定理。
从y中重构x,理论上是解l0范数最小化问题:
min|α|i0s.t.y=Φφα
(2)
其中常用的求解方法有BP算法、TV算法、MP算法、OMP算法和SLo算法等[5,7]。
当N较大时该优化问题成为Nhard问题,为解决这个难点,可通过解l1范数问题近似替代原问题的求解:
(3)
1.2 超混沌Chen系统
Chen系统是一个典型的连续型超混沌系统,它与Lorenz系统类似,但不拓扑等价而且更复杂。在应用过程中,需要进行离散化处理,主要处理方法是利用四阶龙格库塔法。Chen系统的表达式为:
(4)
当参数a=36、b=3、c=28、d=16和-0.7≤k≤0.7时,式(4)处于超混沌状态。通过设定{a,b,c,d,k}这5个参数,将{x,y,z,w}的初始值作为加密系统的密钥。
1.3 置乱
置乱就是只改变像素点的位置,如行置乱和列置乱,而不改变像素点的值。
1.3.1 置乱算法1。明文图像经过稀疏化操作后,进行简单的Arnold置乱。张玉书等[6]已经证明,将明文图像在稀疏基下的系数矩阵先进行置乱,再进行压缩感知测量,可有效放松测量矩阵的有限等距性能RIP,从而提升恢复图像的质量。其表达式是:
(5)
Arnold矩阵格式:
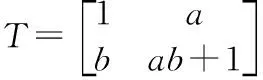
(6)
Arnold矩阵的逆矩阵格式:
(7)
式(5)~式(7)中,(x0,y0)、(x1,y1)分别表示置乱前、后的像素点位置;a和b是混沌系统产生的伪随机整数序列;M和N表示图像的行数和列数。
1.3.2 置乱算法2。明文图像经过压缩感知处理后的矩阵A,然后进行置乱算法2进行置乱加密,其过程如下:
①对于矩阵A中的任一个坐标点(i,j),i=1,2,…,N,计算矩阵A的第i行和(除去A(i,j)),并计算矩阵B的第j列的和(除去A(i,j)),分别记为Ri和Hi。然后,计算一个新的坐标点(m,n),按下述的条件:
如果jmod2=1,那么m=(HjmodM)+1,n=(RimodN)+1。
如果jmod2=0,那么m=M-(HjmodM),n=N-(RimodN)+1。
如果m=i或n=j,则B(i,j)位置不变;否则对换A(i,j)和A(m,n)。
②按从左到右、从上到下的扫描方式遍历矩阵A,依次循环执行步骤①,实现置乱操作。
1.4 扩散
扩散处理是在不改变像素点位置的条件下,将任一明文信息隐藏在尽可能多的密文像素点中。本方案中采用基于加取模和循环左移运算的前后双向扩散运算。
前向(按i从1到MN)扩散及其逆运算为:
Ci=(Ci-1+Si+Pi)mod<< (8) Pi=(2×256+Ci-Ci-1-Si)>>>LSBk1(Pi-1) (9) 后向(按i从MN到1)扩散及其逆运算为: Ci=(Ci+1+Si+Pi)mod<< (10) Pi=(2×256+Ci-Ci+1-Si)>>>LSBk1(Pi+1) (11) 式(8)~式(11)中,M和N表示图像的行数和列数;Si分别代表混沌系统生成的伪随机整数序列、密文图像的像素值;Ci、Ci-1、Ci+1分别表示密文图像的当前像素值、前向扩散和后向扩散的像素值;Pi、Pi-1、Pi+1分别代表明文图像的当前像素值、前向扩散和后向扩散的像素值;k1代表移动的位数,其取值范围是0≤k1≤7。 压缩感知理论中稀疏基和观测基不相关,则很大程度上保证了RIP特性。目前常用的测量矩阵还有随机贝努利矩阵、部分正交矩阵、托普利兹和循环矩阵和稀疏随机矩阵等。 本方案中测量矩阵产生的过程如下: 由式(4)中产生M+k2的混沌序列,舍去前k2项得到y; 其取值范围是0≤k2≤255; 对y的元素按从大到小的顺序进行排序,得到索引序列s。根据s重排自然序列n=[1,2,…,M],得到序列n1。 对I2进行均匀量化得到I3,I3值的范围限制在0~255之间的整数。其中可以通过控制不同的k2实现不同测量矩阵的观测。k2是一个变参数。 本方案将压缩感知理论和图像混沌加密算法紧密融合,在保证图像传输和存储安全性以及图像恢复质量的前提下,提高了图像加密和解密的速度,在大数据的背景下,有效地减少了数据量的传输和保存。基于此,本设计方案包含明文图像稀疏化、系数置乱、压缩感知观测、像素点置乱和双向扩散等五部分。其中置乱、压缩感知观测、扩散过程中由超混沌Chen系统产生的密钥流控制,混沌系统的初始值以及变参数作为密钥,通过秘密信道发送给接收方,其流程如图1所示。 图1 基于压缩感知的图像混沌加密流程 设输入的明文图像记为P,大小为M×N,密钥是超混沌Chen系统的初始值{x0,y0,Z0,w0}和(k1,k2)。具体步骤如下:①将明文图像P,经过正交基矩阵稀疏化操作后,得到大小为M×N的稀疏化矩阵C1。②利用Chen混沌系统产生的长度为M×N×2的伪随机序列X,分为两个为长度为(M/2)×(N/2)的a和b,并带入到置乱算法1中,按照1.3.1对C1的每一个元素进行置乱操作,得到矩阵C2。③利用Chen混沌系统产生为长度为M+k2的伪随机序列Y,传入变参数k2,按照1.5节所述方法构造大小为M×N测量矩阵Φ。④用测量矩阵Φ对矩阵C2进行压缩感知测量,得到大小为M×N个矩阵C3。⑤利用Chen混沌系统产生的长度为M×N的伪随机序列Z,按照1.3.2节所述方法应用到置乱算法2中,得到矩阵C4。⑥传入变参数k1,利用Chen混沌系统产生的长度为M×N×2的伪随机序列W,分为两个均为M×N的伪随机序列W1和W2,W1应用在前向扩散中得到矩阵C5,矩阵C5旋转180°后得到矩阵C6,W2应用在前向扩散中得到矩阵C7,矩阵C7旋转180°后得到矩阵C,即为密文图像。 解密是加密的逆过程,其过程简述如下:①将接收到的密文图像C,利用接收到的密钥,分别进行180°旋转、后向扩散的逆运算、180°旋转、前向扩散的逆运算得到明文图像P1。②利用接收到的密钥k2,将明文图像P1的列向量进行重构,得到明文图像P2。③对明文图像P2进行置乱还原和基于某一正交基下的稀疏化操作逆运算后得到明文图像P3。 采用标准测试图像进行仿真实验,验证方案的安全性能和压缩性能。实验采用的硬件平台包含Windows7操作系统,Intel 酷睿i5-4200U+2.6GHz处理器、1T硬盘、8GB内存,MATLAB2016a。设置密钥{x0,y0,Z0,w0,k1,k2}分别为{0.3388,0.8967,32.1234,0.7425,3,212},稀疏基采用离散小波变换(DWT),由于对图像信息进行稀疏化的过程中通过小波变换来实现,小波变换的级数和阈值的设置对图像的恢复质量有较大的影响,因此,经过多次试验,离散小波变换(DWT)的级数和阈值分别设置为7和3.2,对于图像重构的质量较好,重构的算法采用的是正交匹配追踪(OMP)算法,取压缩比为2∶3,测试图像采用图像大小为256×256的Lena、Peppers、Brain。如图2所示是本方案的仿真结果,实验证明,本方案能同时完成图像的压缩和加密,且保证了图像的重构质量,效果良好。 (a)Lena明文图像 (b)加密的Lena图像 (c)解密的Lena图像 一个良好的图像加密算法必须要有足够大的密钥空间来抵抗暴力统计攻击,当密钥空间大于2100才能保证其密钥空间的安全性,本方案中的密钥是K={x0,y0,Z0,w0,k1,k2},其中,x0∈(-45.5988,41.2199),y0∈(-58.2307,60.2309),Z0∈(10.1560,129.6872),w0∈(-4.6467,23.7265),k1∈[0,7],k3∈[0,255],x0,y0,Z0,w0的步长均为10-3,k1,k2的步长均为1,因此密钥空间大小约为2200≫2100。 直方图分析是衡量一个图像像素值的统计特性,密文图像的统计特性尽可能均匀分布,以抵抗统计分析。如图3所示,三幅图像的明文图像的直方图起伏变化明显,加密后的图像直方图与原图像有很大不同,其像素值均匀分布,可以有效地抵抗统计攻击。 (a)Lena明文直方图 (b)Lena密文直方图 一般地,明文图像在水平、垂直、正对角和反对角方向上的相邻像素间均具有较强的相关性,而密文图像中的相邻像素点间应没有相关性。加密后的图像其相关性变低,如表1所示是Lena、Peppers、Brain图像及其密文图像,随机选取3 000对相邻像素在水平、垂直、正对角和反对角方向上的测试结果。 表1 Lena、Peppers、Brain明文和密文图像的相关系数 表1表明本算法能有效地降低相邻像素间的相关性。 差分分析的目的是检验加密算法是否可以有效地抵御差分攻击。其判定指标是图像像素值变化率(NPCR)和归一化像素值平均改变强度(UACI)。其表达式是: (12) (13) 通过测试,得到本方案中加密算法的NPCR和UACI分别为99.5627%、33.4625%,而NPCR和UACI的理想期望值是99.6094%、33.4635%,对比不同文献,可以明显看出明文对密文存在雪崩效应,密文对明文的细小变化存在高度的敏感性。 运行效率是指图像在加密过程和解密过程中所消耗的时间,本方案所设计的图像混沌加密算法和基于压缩感知的图像混沌加密算法,彼此做对比实验,其中以Lena图像为例,如表2所示,从表2可以总结出本方案在图像加密和解密过程中效果良好,在保证图像重构质量的前提下,加快了加密和解密过程中的速度。 表2 Lena图像加密时间对比 单位:秒 笔者提出了一种兼顾压缩性能与安全性能的加密方案,实现了图像的同步加密与压缩,其主要特点是将压缩感知理论和图像混沌理论相结合,在大数据时代下,有利于图像信息的传输和存储。通过对本方案仿真实验结果的直方图分析、相关性分析、差分分析、峰值信噪比分析等性能分析,结果表明,图像在加密过程中,在保证图像信息质量的前提下,提高了加密和解密的速度,验证了本方案的可靠性、安全性以及鲁棒性。1.5 构造测量矩阵

2 加密和解密步骤
2.1 总的设计方案
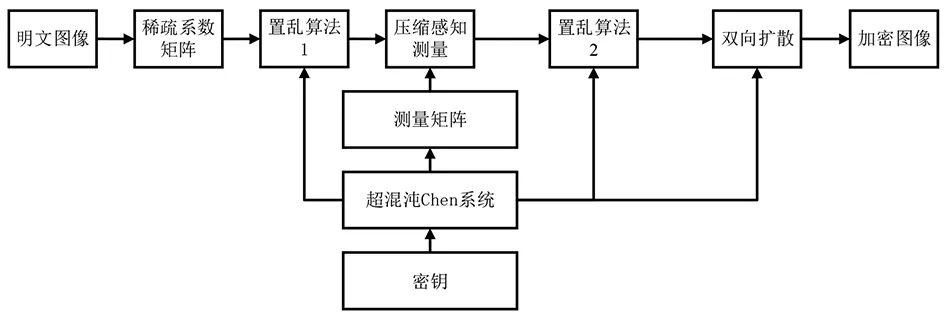
2.2 加密步骤
2.3 解密步骤
3 实验仿真及其安全性能分析
3.1 基于压缩感知的图像混沌加密仿真实验

3.2 密钥空间分析
3.3 直方图分析

3.4 相关性分析
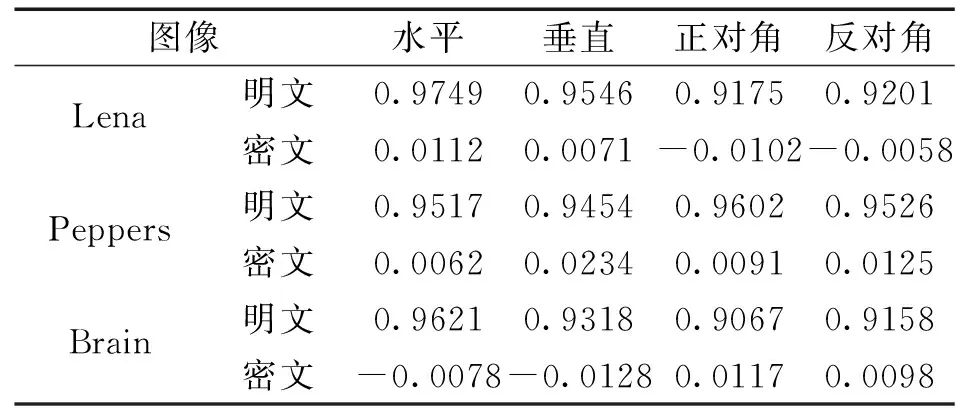
3.5 差分分析
3.6 运行效率
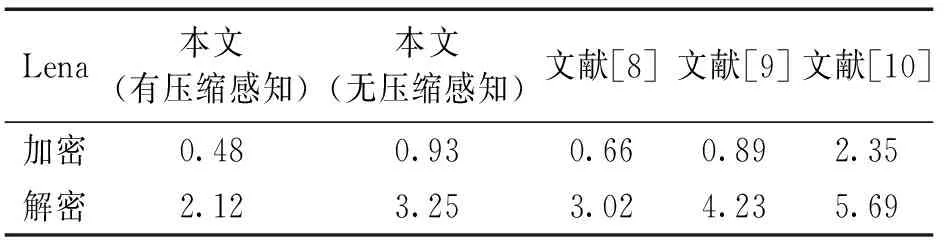
4 结论
