基于复杂度差异的VVC中360度视频CU划分快速决策
2021-07-28张晨昕
张晨昕
(北方工业大学,北京 100144)
0 引言
随着虚拟现实(VR)技术的进步,全向视频(360度视频)在最近几年越来越受欢迎。其内容通常在经度上跨度360度,在纬度上跨度180度。摄像机捕获的视频导出后进行图像拼接以获得球形场景,然后将其投影到2D平面上进行编码[1]1241。随着新一代视频编码标准VVC的到来,VCEG和MPEG发布了新一代视频压缩技术提案征集(CFP)[2],等距柱状投影(ERP)是CFP中使用的所有360度视频序列的源投影格式,也是使用最广泛的投影格式,但其视频压缩效率并不高,由于在两极区域过采样,存在大量对编码效率产生负面影响的冗余。
VVC标准有望提供高效的360度视频编码解决方案,非常适合解决虚拟现实视频应用不断增长的需求[1]1250。与HEVC不同,VVC中引入了四叉树嵌套多叉树(QTMT)的划分结构,由于非对称分区的引入,编码的计算代价与时间代价也是巨大的,在全帧内测试配置下,VVC测试软件(VTM)的帧内编码复杂度是HEVC测试软件HM的18倍[3]。仅禁用二叉树划分模式(BT)后,编码时间平均节省75.3%;仅禁用三叉树划分模式(TT)后,编码时间平均节省47.6%;同时禁用BT与TT,编码时间平均节省91.7%[4]。不论是对于普通视频还是360度视频,优化CU划分过程采取的方法主要分为2类,即传统的人工特征提取方法和基于学习的方法。一方面,传统的人工方法如文献[5]、文献[6]提取的特征包括已编码CU的深度、图像纹理特征等,通过比较特征快速决策CU分区;另一方面,随着机器学习技术的发展,基于学习的方法也涌现了出来[7-8]。但是,在VTM的编码过程中生成了长与宽不相等的各类矩形,因此,使用网络进行学习将大大增加参数量,并导致计算的复杂性显著上升。借鉴文献[9]统计CU深度分布的思想,对于360度视频分纬度统计CU深度的分布,笔者考虑数据量大的特点,选用计算复杂度较小的传统方法,提出了一种基于纹理复杂度的多叉树划分决策快速算法。
1 纹理复杂度的计算与CU深度分析
1.1 纹理复杂度的计算
在计算CU的纹理复杂度的研究中,传统方法主要使用方差特征或梯度特征来检测纹理[10-11]。由于虚拟现实360度视频分辨率高,画面细节丰富,为了计算CU的纹理复杂度并相互比较,需要更加突出纹理区域。作为梯度算子,scharr算子系数更高,纹理权值更大,进一步增强了边缘特征,并且获得了更清晰的信息[12],在这方面比sobel算子更为优秀,所以笔者选用scharr算子计算CU的纹理复杂度,如式(1)~式(3)所示。
(1)
(2)
Gscharr=|Gx|+|Gy|
(3)
式(1)~式(3)中,Sx和Sy分别代表水平和垂直方向的scharr算子;W和H分别为当前CU的宽和高;A为3×3的亮度值矩阵;Gx表示水平梯度;Gy表示垂直梯度;Gscharr表示块的总梯度。
为了判断CU简单或复杂,需要寻找判断阈值,在虚拟现实360度视频场景下,不同纬度的拉伸情况不同,传统方法使用固定阈值判断CU简单或复杂不合理,为了使CU划分方式的判断结果更加符合实际情况,需要对不同纬度的CU设置不同的阈值。CU纹理复杂度与CU深度有很强的相关性,所以笔者对不同纬度CU深度进行了统计分析。
1.2 ERP投影格式下的360度视频CU深度分析
CU深度分为四叉树深度(qtdepth)和多叉树深度(mtdepth),它们分别表示了1个CU执行四叉树划分和多叉树划分的次数,默认的四叉树深度可以从0增加至4,在完成四叉树划分之后才能开始多叉树划分,并且四叉树深度不再改变。在ERP投影格式下的虚拟现实360度视频中,位于两极区域的图像被水平大幅度拉伸,导致纹理相对均匀且简单,示例块使用四叉树深度较浅的CU进行编码;相比之下赤道区域拉伸程度较轻,图像纹理相对复杂,示例块使用四叉树深度更深的CU进行编码。不同纬度区域CU划分结果示例如图1所示,CU划分结果说明如表1所示。

表1 CU划分结果说明
笔者定义四叉树深度1和2的CU为较浅CU,四叉树深度3和4的CU为较深CU,为了研究纬度和CU四叉树深度的关系,进行了一系列统计工作。对每帧图像垂直间隔128个像素点划分纬度带,4 K图像有15个纬度带,6 K图像有24个纬度带,8 K图像有32个纬度带。4 K,6 K,8 K视频序列在量化参数QP=22,27,32,37这4种情况下,不同纬度较浅CU(qtdepth≤2)的占比情况如图2所示。
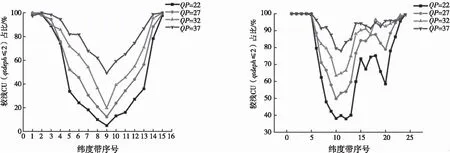
(a)4 K视频序列CU分布情况 (b)6 K视频序列CU分布情况
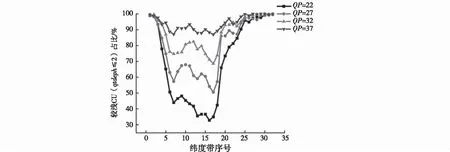
(c)8 K视频序列CU分布情况图2 360度视频CU分布情况统计图
从图2可以看出,3种分辨率的视频两极CU全都普遍较浅,占比达90%以上,且随着纬度向赤道靠近,较浅CU占比逐渐下降,相对较深CU占比逐渐增加。同时不同纬度带CU占比与QP相关性很大,QP越小,CU的四叉树深度总的来看更深;QP越大,总的来看CU的四叉树深度越浅。
笔者发现cos函数在[0,2π]区间内大致符合上述变化规律,可以拟合上述曲线,如下:
y=αcos (2πx/β)+γ
(4)
式(4)中,y表示较浅CU占比;x为纬度带序号;α,β,γ是预设参数。
上述函数曲线可以区分不同纬度下四叉树深度较浅与较深CU的划分比例。显然,同纬度中四叉树深度较浅CU一般纹理简单,较深CU一般纹理复杂,所以该函数可以用来区分不同纬度纹理复杂度低与高的CU。后续过程将以该函数为基础,按纹理复杂度对CU进行分类,并分别决策划分方式。
2 拟议的算法
由于研究的重点是CU是否进行四叉树划分至四叉树深度到达3,所以选取的对象块四叉树深度为2,尺寸为32×32。与之前的统计工作一致,对于任一高度为128的纬度带,用scharr算子计算其中每一个32×32块的纹理复杂度,取其中复杂度最高的块,记为Smax,进而利用拟合的函数定义不同纬度的纹理复杂度动态阈值Dt:
Dt=Smaxαcos(2πx/β)+γ
(5)
预设参数α,β,γ如表2所示。
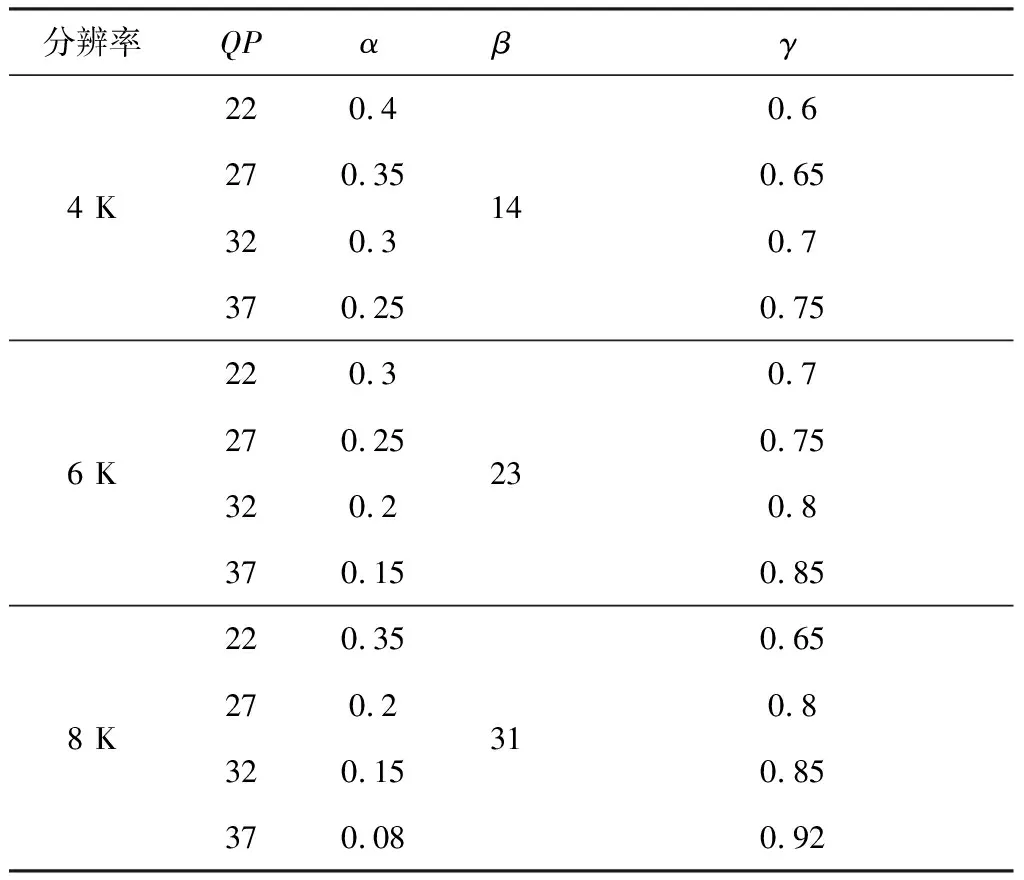
表2 拟合函数参数表
编码过程中,当前块的纹理复杂度Gscharr≤Dt时,判定为纹理简单块,执行四叉树划分至四叉树深度为2后进行多叉树划分;Gscharr>Dt时,判定为纹理复杂块,笔者发现其划分方式存在一定规律,需要进行下一步的判断。
在对32×32的母块CU进行类四叉树的4等分之后,使用scharr算子分别计算4个子块的纹理复杂度,并记录母块CU在原本算法中选择的划分方式。4种典型CU的划分方式及其子块复杂度如表3所示。
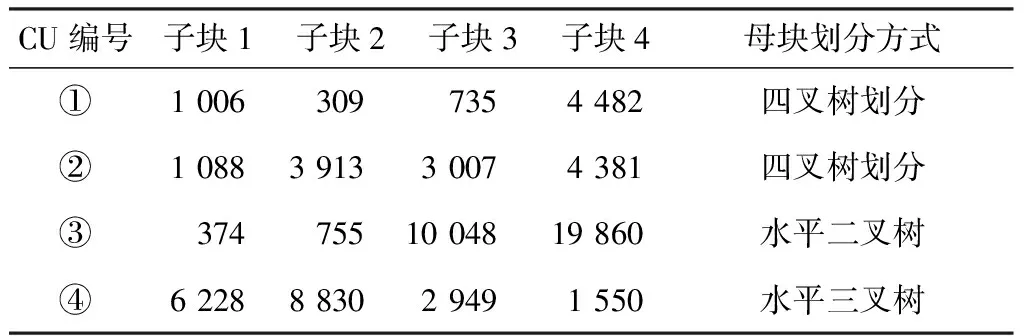
表3 4种典型CU的划分方式及其子块复杂度
从表3中可以看出,①号CU的子块4复杂度非常高,与位于第2高的子块1之比大于4,在这种对比下,子块1~3的复杂度视为在同一数量级;同理,②号CU的子块1复杂度很低,位于第2低的子块3与其之比约等于3,在这种对比下,子块2~4的复杂度视为在同一数量级。在这2种情况下,母块CU均选择了四叉树划分。③号CU子块1和子块2复杂度很低,子块3和子块4复杂度相比之下非常高,比前者高出10倍以上,母块CU选择水平二叉树划分,这时认为在水平方向上,子块1和子块2不含纹理,可以合并,子块3和子块4纹理丰富,也可以合并;类似地,④号CU在水平方向上,子块1和子块2可以合并,子块3和子块4也可以合并,实际上母块CU选择了水平三叉树划分,这是由于三叉树在划分过程中,先后执行了3次同向二叉树划分,视觉上看等效于将母块在水平方向上平均分成4份,而后将中间2份合并。所以无论是三叉树还是二叉树,在划分过程中纹理复杂度相对较大和较小的2个相邻子块都可以视为合并。
由此,针对复杂CU,总结出基于子块复杂度的多叉树划分判断方法:对于4个正方形子块,分别计算它们的纹理复杂度,记为:Sub1,Sub2,Sub3,Sub4,其中,Sub1代表最小值,Sub2代表次小值,Sub3代表次大值,Sub4代表最大值,将判断复杂度之比的阈值记作Th,则判断条件总结如下:
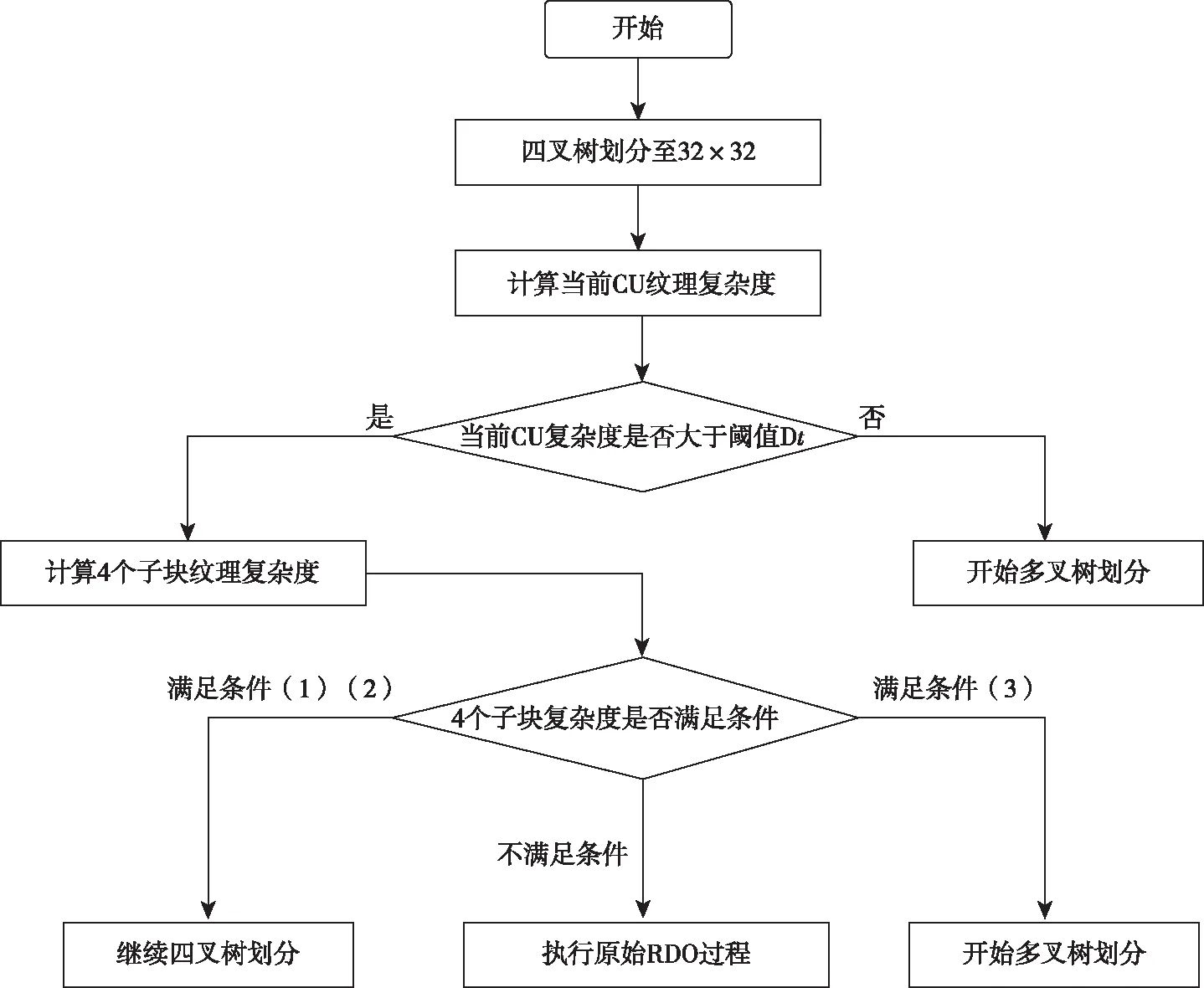
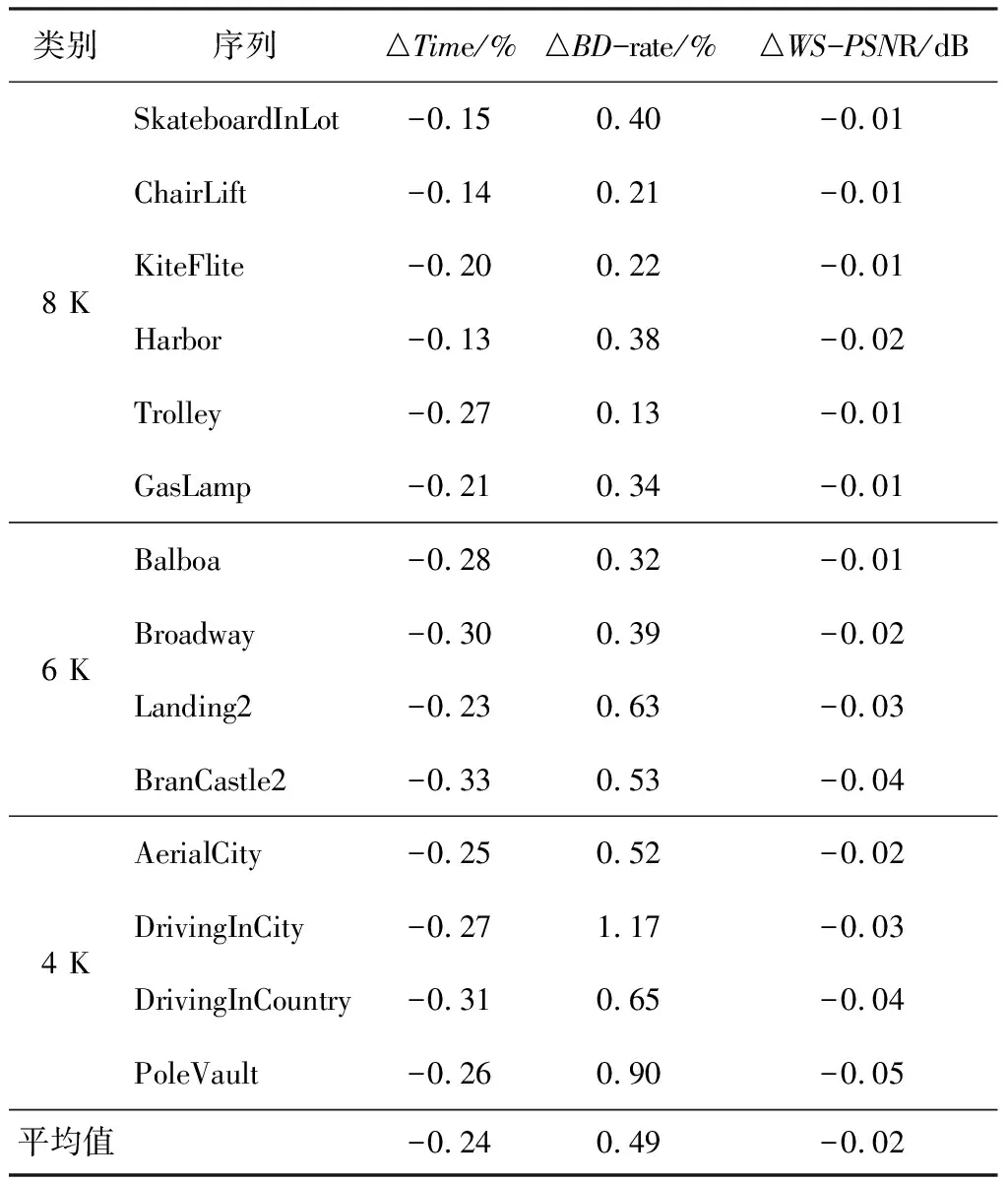
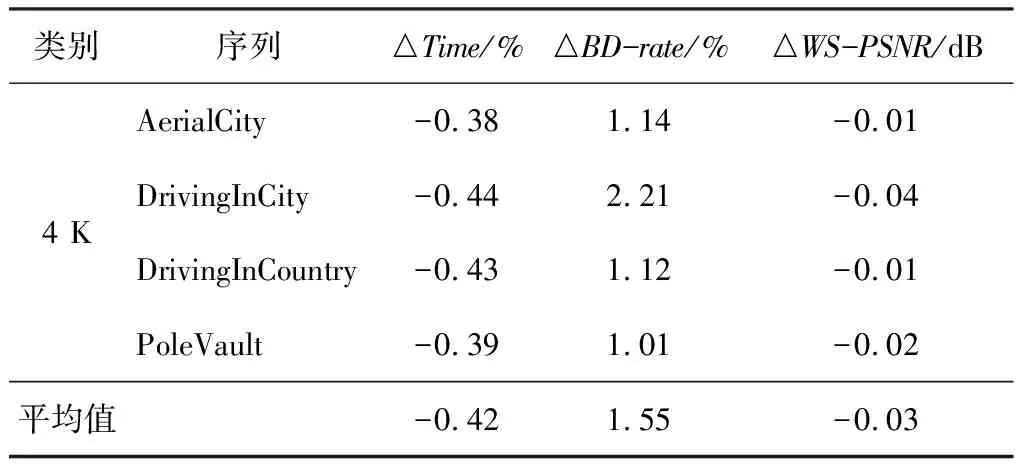
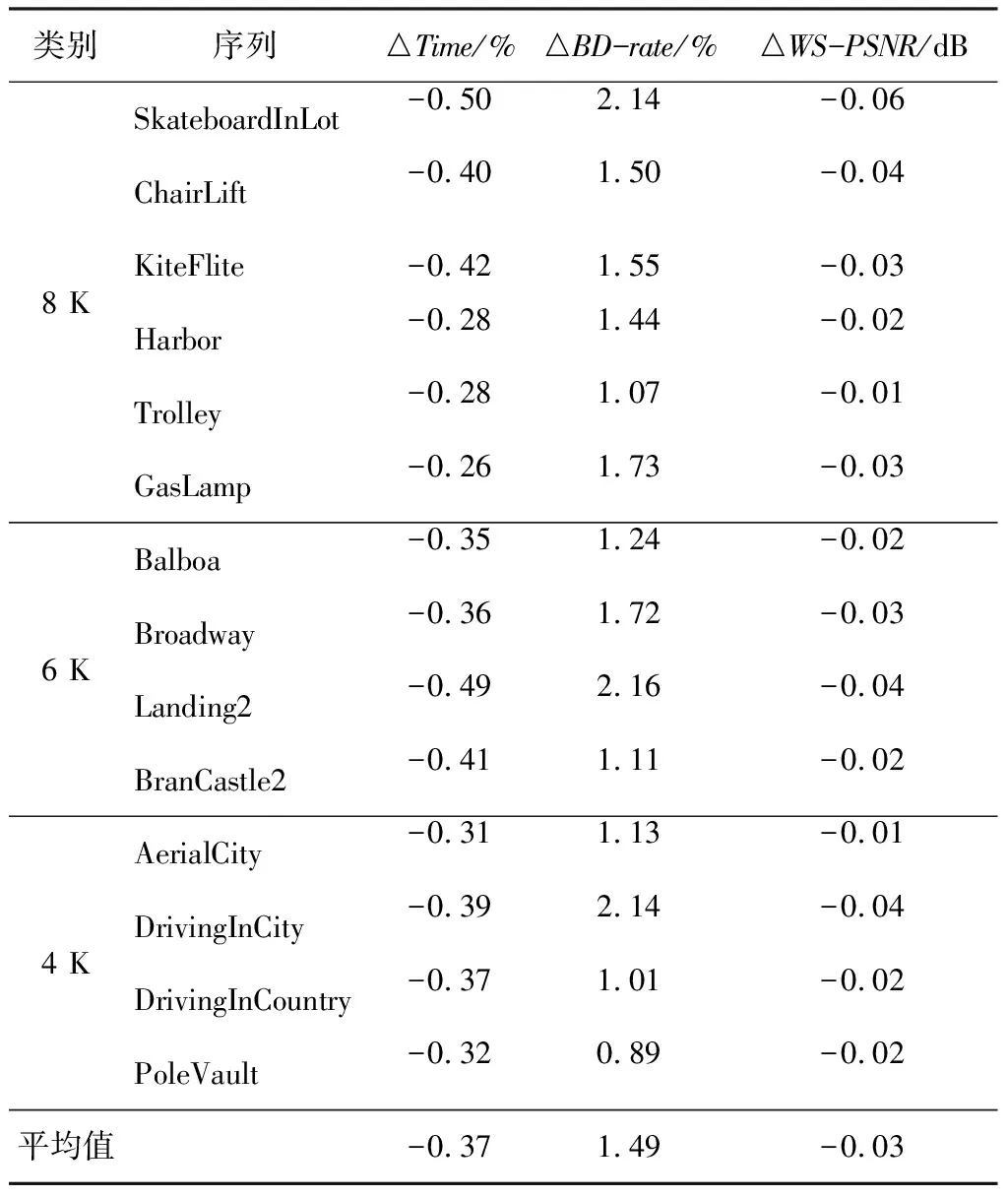
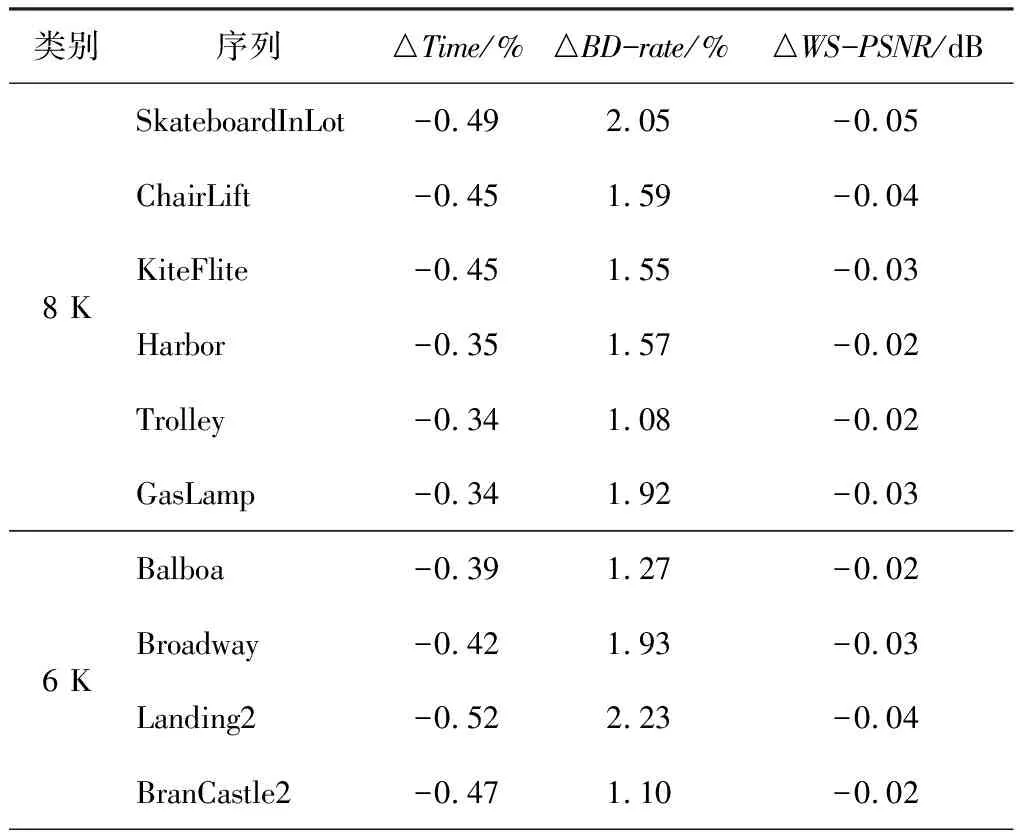
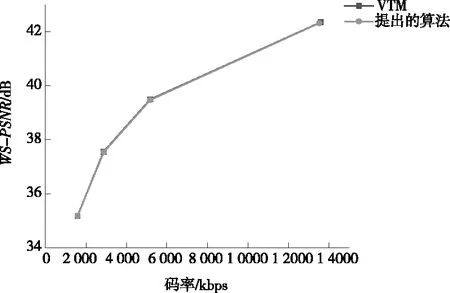
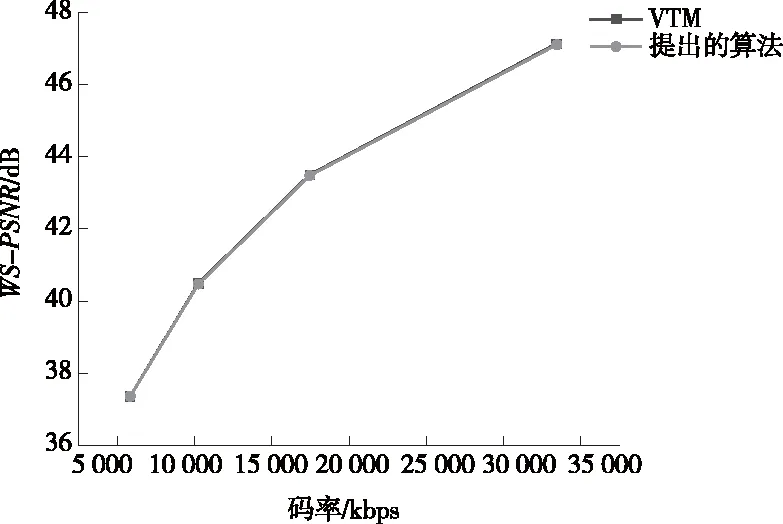
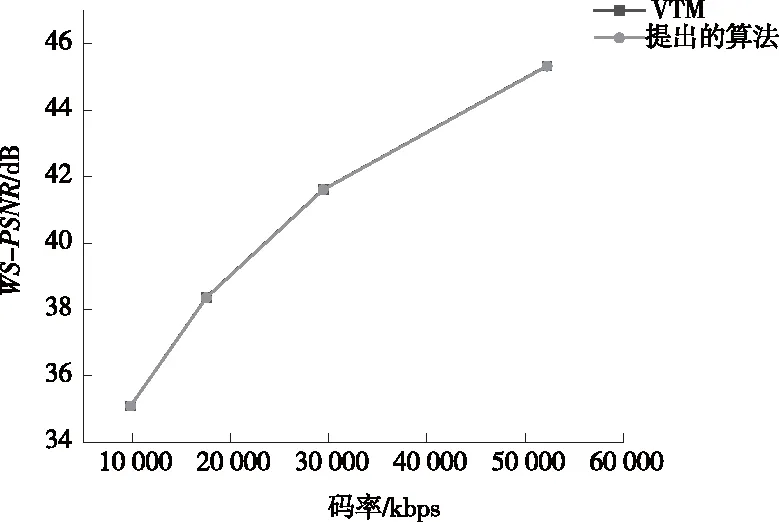
(1)Sub4/Sub1 (2)Sub4/Sub3>Th1或Sub2/Sub1>Th(Th1=Th+1); (3)Sub4/Sub3和Sub2/Sub1 条件(1)表示:Sub4与Sub1在同一数量级,无明显大小关系,则所有子块复杂度均在同一数量级,视作大小接近,应选择四叉树划分;条件(2)表示:某一个块复杂度大小比其余块更为突出,应选择四叉树划分;条件(3)表示:2组位置相邻的2块之间复杂度无差异,2组之间复杂度有差异,应选择多叉树划分。 笔者验证了不同阈值下,该条件判断的正确率,其结果如图3所示。 图3 不同阈值下条件判断正确率 图3曲线为用笔者总结的判断条件判定的划分方式与原算法判定的划分方式一致的概率,可以看出4 K,6 K,8 K这3种分辨率的视频均在Th=2时,有较高的判断正确率。其原因是当Th过小时,条件(1)的判断与描述更加符合,更容易筛选出4个子块复杂度接近的CU做四叉树划分,而判断条件(2)与判断条件(3)所需的差异性体现得不明显;Th增大到2时,条件(1)选出的CU子块之间复杂度仍较为接近,其正确率保持较高水平,而判断条件(2)与判断条件(3)所需的差异性逐渐明显,可以筛选出代表性的CU,正确率上升;随着Th增大,条件(1)选出的CU子块之间复杂度不再接近,其正确率下降,对于条件(2)与条件(3),用于筛选典型块的条件越来越严格,选出的块数量越来越少,而用来保证其余块互相接近的条件越来越宽松,导致存在差异的块被误判选中,造成正确率下降,所以总体来看,Th=2时正确率最高。 整体算法流程图如图4所示。 图4 基于复杂度差异的VVC中360度视频CU划分快速决策算法流程图 在实验中,笔者将提出的算法合并到版本最新且稳定的VTM-8.0和与之对应的360Lib-10.1中进行测试。实验的主要编码参数为全I帧编码模式,初始QP分别为22,27,32,37。使用JVET发布的Excel表计算BD-rate,用来综合表示图像质量与码率的情况,△BD-rate为正表示性能损失,并使用基于纬度加权的峰值信噪比(WS-PSNR)衡量图像质量,△WS-PSNR的计算如下: ΔWS-PSNR=WS-PSNRproposed- WS-PSNRVTM8.0 (6) 改进后算法与原始算法的时间比较用△Time来表示,计算方法如下: (7) 提出方法与原始VTM8.0的比较结果如表4~表6所示。 表4 全I帧模式 表5(续) 表6 randomaccess模式 表4中,在全I帧模式下实验结果表明:与原始算法相比,笔者提出的算法的编码时间平均节省了24%,WS-PSNR平均降低了0.02 dB,BD-rate平均仅增加0.49%,可以看出对于BranCastle2,Broadway,DrivingInCountry,Trolley等赤道区域比较复杂的视频,笔者提出的算法的加速效果较好,对于其他赤道区域纹理不明显、空旷区域较大的视频效果较差。这是由于笔者提出的算法主要加快了纹理复杂CU的划分方式决策速度,而简单CU的划分决策速度与原算法相似。表5、表6显示对于lowdelay模式和randomaccess模式,笔者提出的算法对原始算法也有大幅时间减少。全I帧模式下不同序列的率失真(Rate-Distortion,RD)性能曲线比较如图5所示。 表5 lowdelay模式 (a)4 K视频AerialCity率失真曲线 (b)6 K视频Broadway率失真曲线 (c) 8 K视频Trolley率失真曲线图5 实验视频序列率失真曲线图 从图5可以看出,使用本算法编码的视频质量几乎与原始VTM算法相同,没有明显损失。 为了解决VVC编码标准在虚拟现实360度视频场景下编码时间长、复杂度高的问题,针对ERP投影格式的特点,笔者设计了一种CU划分方式快速决策算法,通过统计分析不同纬度CU划分结构的分布特征,利用梯度计算CU的纹理复杂度,在各个纬度区分简单与复杂CU,决定简单CU的划分方式,而后通过统计分析复杂CU划分结构与子块复杂度间的关系,进一步判断复杂CU的划分方式。通过提前决策CU的划分方式,降低原有算法的计算量来节省编码时间,提升编码效率。实验结果表明:在全I帧模式下,与现有的VTM8.0相比,时间节省了24%,WS-PSNR降低了0.02 dB,BD-rate仅增加了0.49%。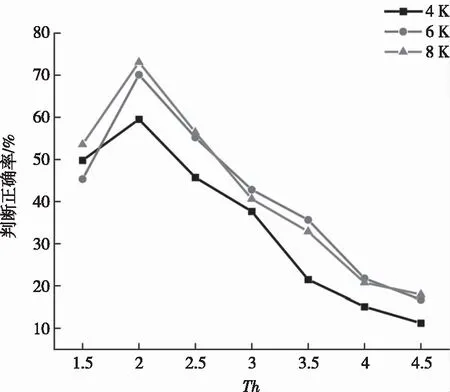
3 实验与分析
3.1 实验数据与评价标准
3.2 实验结果分析
4 结论
