考虑动态重构的装备体系可用性及弹性分析

陈志伟, 王 靖, 谷长超, 章健淳, 钟季龙

(1.中国运载火箭技术研究院, 北京 100076; 2.北京航空航天大学杭州创新研究院, 浙江 杭州 310051;3.军事科学院国防科技创新研究院, 北京 100091)

0 引 言

随着诸如军事体系、交通体系、社会技术体系等越来越多的复杂“巨系统”——体系的出现,使其成为了当前信息物理系统和复杂大系统研究的热点,尤其在现代军事领域中,体系得到了最早和最为广泛的应用[1-2]。随着现代化战争形态及军队建设的转型发展,现代化作战早已从单一兵种作战转变为多种武器、多兵种的一体化联合作战,从以平台化作战转变为以网络为中心的体系化作战。因此,如何保障体系持续稳定地有效运行变得至关重要。新的系统或体系级属性概念弹性地出现,为解决体系相关问题提供了新的研究思路。

动态重构是典型的装备体系弹性恢复策略,也是装备体系弹性的主要表现形式。动态重构最初是由美国国家航空宇航局于1982年提出,并指代一种软件的容错技术。现阶段,重构技术已经广泛应用到工业自动化和控制系统、自动化信息物理系统和体系当中[3-4]。因此,装备体系需要在考虑物理过程复杂性和系统演变性的同时,确保这些重新配置、诊断和预测功能可以持续有效地运行[5-6]。本文将动态重构作为装备体系弹性研究的输入,分析装备体系在动态重构下的弹性是如何变化的。弹性主要源于体系的组织和拓扑的结构属性,能够帮助体系规避致命损害、在扰动中存活、从故障和失效中恢复,进而继续完成体系的任务使命。可以说,装备体系弹性的本质就是装备体系在遭受内外部干扰后的动态重构。

弹性(resilience)的英文词源起源于拉丁语的“resiliere”,其在英文中的首次使用可以追溯到17世纪初,意为“反弹的动作”[7-8]。Hollnagel等[9]最早对工程领域的弹性概念和理论进行了研究,并于2004年在瑞典举办了第一次弹性工程研讨会,成立了第一个弹性工程协会,并将弹性定义为“系统或组织在早期阶段对干扰作出反应和从干扰中恢复的能力”,其他文献[10-11]也有较为类似的定义。美国国防部认为弹性是“抵御、抵抗、吸收能力,恢复能力,适应能力和广泛实用性”4个属性的体现[12-13],其中前3个属性与工程系统的弹性观点一致,而第4个属性则揭示了国防部对其设备在不同环境下运行的要求。现阶段,对装备体系弹性建模研究的主要应用包括马尔可夫链、离散事件仿真、Petri网、系统动力学模型、复杂网络理论等[14-19]。潘星等[20]利用复杂网络理论进行体系弹性分析,提出了基于弹性的组件重要度分析方法,并分析权衡了性能损耗与恢复时间对组件重要度的影响,从而构建了评价体系弹性的恢复策略优化方法。Pan等[21]将作战循环数作为性能指标，对网络化体系开展基于弹性的重要度评估,并提出一种基于邻接矩阵特征值的近似算法来计算作战循环数。张强等[22]研究了基于复杂网络理论的动态链接网络结构性能,并提出了动态连接增益对作战网络模型的评价与优化。杨克巍等[23]对国内外武器装备体系贡献率评估方法进行综述,并分析对比了不同评估方法的优劣。张俊[24]利用美国国防部架构框架(Department of Defense Architecture Framework, DoDAF)视图产品进行体系结构建模,并将其转化为赋权有向图,对装备体系关键节点进行评估。程贲等[25]对装备体系优化设计的国内外研究现状进行了综述,并对7种体系优化方法进行了比较,并提出了体系优化现阶段尚需解决的4个关键问题。同时,多状态权重k-out-of-n系统是最为典型的多状态系统模型,例如,某些类型的电力系统、计算机系统、管道输送系统和信号传输系统等多状态系统[26]。这些系统具有运行周期长、生产和维护成本高等特点,因此对多状态权重k-out-of-n系统进行可用性或弹性分析显得尤为重要。

在此研究背景之下,虽然装备体系弹性的相关研究迅速发展,但通过调研分析表明,目前对装备体系弹性的定义、识别、评估、实现弹性方法等研究仍处于初期阶段。本文根据装备体系层次化特点,从装备体系物理资源和功能性能两个角度建立装备体系弹性多层级评价方法。资源层以各作战平台的物理资源为研究对象,以资源共享为核心,研究考虑动态重构情况下的装备体系资源状态变化,通常采用基于复杂网络理论的方法对物理资源层弹性进行研究;性能层以组成系统特定能力的性能指标为研究对象,关注各类系统或设备的性能变化,在考虑动态重构情况下研究各同类系统综合性能指标变化的弹性,通常采用随机过程、多状态空间理论等方法对功能性能层弹性进行研究。

本文首先建立装备体系多层级评价框架,明确装备体系弹性研究的层次结构,并以典型的装备要素——编队作战体系武器系统进行可用性及弹性分析。然后,根据通用生成函数(universal generating function,UGF)和Markov过程构建基于动态双阈值多状态权重k-out-of-n系统模型(D-Model III)的装备体系性能可用性及弹性分析评价方法。最后,以编队协同防空作战体系为对象进行案例应用研究,得到典型装备要素武器系统的可用度和弹性变化规律,并验证了所提模型与评价方法的有效性。

1 装备体系弹性多层级分析

1.1 多层级评价框架

弹性在本文中既是装备体系自身的一种属性,也是一种评价和度量指标。本节根据装备体系层次化特点,从装备体系物理资源和功能性能两个角度建立装备体系弹性多层级评价方法。本文将体系分解为任务使命层、平台资源层和功能性能层3个层级,梳理出自上而下的完整映射关系。由于论文篇幅限制,本文仅针对装备体系性能层典型装备要素开展相关应用研究。

武器装备体系具有一个体系使命由若干物理资源协作完成、一个平台资源支撑多个功能性能以及一个功能性能可由若干物理资源协同实现的特点。因此,本文将装备体系分解为体系任务层、平台资源层和系统性能层3个层级,梳理出自上而下的完整“体系-资源-性能”映射关系,如图 1所示。其中,装备体系的性能层关注的是各类系统或设备的性能变化,资源层关注系统或平台资源实体之间的协同能力,体系层则综合协调体系的功能性能和物理资源弹性,关注作战任务全局的弹性能力。

图1 装备体系弹性多层级评价框架

1.2 基于性能阈值的弹性量化模型

基于性能阈值的弹性量化模型是从功能性能角度出发,根据多维度弹性理论[27]和动态弹性度量模型[28],通过对各装备要素的性能指标变化情况提出的基于性能阈值的弹性量化模型[29]。

弹性累积损失量表征在任务过程中,即体系遭受干扰后性能损失量的总和,如图2中的阴影部分所示。

图2 基于弹性的性能水平变化过程

当体系输出性能低于k时,无法满足最低运行条件,体系已经不具有弹性,低于阈值部分的性能损失不计入累积损失量。弹性累积损失量Rl的计算公式为

(1)

当发生干扰后,体系所能承受的最大性能损失量为弹性裕度,记为Rlimit,即体系以完好状态运行和以最低性能状态运行的差值与任务持续时间的乘积:

Rlimit=(g0-k)·(ts-t0)

(2)

体系的弹性R可以表示为

(3)

式中:0≤R≤1,当R=1时,表示体系没有弹性损失,处于完好运行状态;当R=0时,表示体系已无弹性处于临界崩溃状态。

2 装备体系性能层弹性分析

本节从“功能性能”角度出发,以装备体系中各同类组成系统的性能要素为研究重点,开展考虑动态重构的装备体系性能层弹性分析与评价研究,揭示装备体系各组成系统的性能及弹性变化规律。由于武器体系结构复杂,协同平台复杂,且受篇幅所限,本文以装备体系作战平台的武器系统为典型对象进行分析研究。

装备体系的网络中心性使武器系统在作战任务过程中可以进行动态重构,相互替代，互为备份,动态调整配置其火力资源,实现协同作战。对装备体系武器系统组成的火力网评价需要选取合适的性能指标,基本火力指数也称单项火力值,可以用来衡量一个武器杀伤力[30]。在忽略各平台间通讯链路失效情况下,具有离散状态特性的装备体系火力网可以看作k-out-of-n系统结构。本节给出了考虑动态重构的装备体系武器系统性能、可用性及弹性评价模型。

2.1 系统模型分析

本节假设装备体系中共有n个作战平台,每个平台武器系统具有m+1个性能状态,且m为最佳状态,由于武器系统装载不同数量且具有不同火力指数的导弹,因此其失效或发射一枚导弹都会使火力网性能发生改变。令i为体系中的平台编号,且0≤i≤n,j为体系中不同平台的火力状态,且0≤j≤m。根据作战任务需求,单平台武器系统的性能阈值为kij(t),即为作战任务过程中平台i武器系统保持在性能状态j及以上的最低性能需求,装备体系火力网的性能阈值为Kj(t),即为火力网性能在t时刻保持在状态j及以上的最低性能需求。当作战平台和系统节点间的通讯链路可靠度为1时,可将各平台武器系统组成的火力网假设为一个具有双阈值条件的多状态动态权重k-out-of-n——G系统。

2.2 动态双阈值k-out-of-n系统模型构建

通常情况下,一个多状态权重k-out-of-n系统有n个多状态组件,可修的多状态系统组件可以从高性能状态逐渐退化为低性能状态,也可以通过维修和重构来提升组件性能。根据装备体系火力网结构特征,本节对同时考虑单个组件性能和所有组件累积性能的多状态权重k-out-of-n系统模型[31]进行动态化扩展应用,并命名为D-Model III,具体定义如下:

单个组件的性能不少于组件性能阈值ki，j(t)时,其才能对系统性能做出贡献;同时,当所有组件的累积性能之和大于系统性能阈值Kj(t)时,系统性能才能保持状态j及以上,且阈值ki, j(t)和Kj(t)都随着时间动态变化。

组件i的性能处于状态j可以表示为集合gi={gi,0,gi,1,…,gi,m},双阈值模型的数学定义可以表示为

(4)

式中:φ为系统的结构函数;α(gi,j≥ki,j)为示性函数,可以表示为

(5)

2.2.1 多状态组件建模

本节应用连续时间离散状态的Markov过程来构建多状态组件模型,并通过求解得到可重构组件的状态概率分布。可重构多状态组件i的Markov状态转移模型如图3所示。

图3 可重构组件状态转移框图

组件i的状态概率pij(t)可通过以下微分方程组计算:

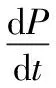
(6)

组件i的状态转移率矩阵Λi为

(7)

各个组件的状态概率和为

(8)

则考虑组件性能阈值ki, j(t)的可修组件i的通用生成函数ui(z,t)可以表示为

(9)

2.2.2 多状态系统建模

组合运算符表示具有性能阈值组件的UGF及其组成结构关系,可得时刻t的多状态系统输出性能分布UGF表示为

Us(z,t)=Ω(u1(z,t),u2(z,t),…,un-1(z,t),un(z,t))=

(10)

式中:Ω是组合算子;φ(·)是多状态系统的结构函数,其计算方法由系统结构决定,例如:串联系统为X=φ(X1,X2,…,Xn)=min{X1,X2,…,Xn},并联系统为X=max{X1,X2,…,Xn},式(10)中的表决系统结构函数可以表示为

(11)

由此,可以计算得到系统在各个状态的性能及其状态概率。

2.3 性能可用性及弹性模型

根据多状态系统的通用生成函数和表决系统结构,可考虑系统性能阈值Kj(t)的多状态权重k-out-of-n系统在时刻t的可用度为A(t),如下所示:

A(t)=Pr{φ(g1, j,1,g2, j,2,…,gn, j,n)-Kj(t)≥0}=

(12)

式中:α(GSj≥Kj(t))为系统示性函数,定义为

(13)

在任意时刻t,系统的平均状态性能为

(14)

根据式(1),可得武器系统的弹性累积损失量Rl为

(15)

根据式(2),可得武器系统的弹性裕度为

Rlimit=(G0-Kj)t

(16)

根据式(3),可得系统弹性R为

(17)

3 案例研究

舰艇编队协同防空作战装备体系(以下简称编队作战体系)是典型的装备体系,其以协同交战为核心进行网络化防空作战,也是未来编队协同防空反导的主要模式。如图4所示的典型编队作战体系结构中,装备体系主要包括侦察探测要素(空中预警机机群、舰载雷达等),通讯要素(通讯卫星、数据链等形成的通讯网络),指挥控制要素(主副指挥控制系统)和火力要素(各型驱逐舰、护卫舰的武器系统等)4类关键要素。本文以典型的5节点编队作战体系为例,对其4个舰载武器系统组成的火力网进行可用性和弹性分析。

图4 编队作战体系结构示意图

在编队作战体系中,指控系统可以根据作战需求统筹各个舰船平台的火力资源,使其发挥整体作战效能,在作战任务过程中随着各舰载武器系统弹药的消耗增加导致火力网剩余性能下降;同时,武器系统也会遭受不同强度的外部干扰和冲击,导致武器系统性能降级或失效。因此,可以认为火力网性能为连续时间离散状态的变量。假设每个武器系统都有4种状态,分别为状态3,状态2,状态1和状态0。状态3表示武器系统处于完美运行状态,状态2表示武器系统处于良好运行状态,状态1表示武器系统处于一般运行状态,而状态0表示该武器系统处于完全失效状态,各平台和系统间的通讯链路可靠度为1,且各平台武器系统只有在状态0时,才会进行修复或重构。在某次作战任务过程中某型驱逐舰和护卫舰武器系统最低性能需求为恒定常数,分别为15,15,10和10。当武器系统火力指数低于阈值时就需要进行修复或火力补给,甚至退出编队作战体系。整个编队作战体系火力网的性能阈值也会随着作战需求和时间的变化而变化。根据上述假设,同时考虑武器系统性能阈值ki，j(t)和装备体系火力网性能阈值Kj(t),该编队作战体系火力网为典型的双阈值多状态权重k-out-of-4系统模型。假设各个武器系统的状态概率变化服从指数分布,可用D-Model III对装备体系火力网进行可用性与弹性分析。

3.1 模型构建

根据调研对不同类型舰船的火力打击能力及其状态转移率进行近似假设,该装备体系4个舰船平台的武器系统状态转移率和性能数据如表1所示。

表1 不同舰船武器系统性能与转移率表

根据式(6)和式(7),可得到微分方程组:

(18)

各个平台武器系统在任务开始时都为处于完美运行状态,可得各武器系统的初始状态概率为

将表1中的数据代入上述微分方程组,并利用Runge-Kutta法的ODE45对4个平台武器系统的状态概率分布进行求解,得出概率分布结果如图5所示,任意平台在任意时刻的各个状态概率和都为1。

图5 各平台武器系统的状态概率分布

根据式(10),4个舰载平台武器系统性能的UGF可以表示为

(19)

根据式(11),4个舰载平台组成火力网的UGF可以表示为

Us(z,t)=Ω(u1(z,t),u2(z,t),u3(z,t),u4(z,t))=

(20)

3.2 结果与分析

本节分别在性能阈值随时间变化和动态变化两种情况下对装备体系火力网相关参数进行分析,具体如下。

3.2.1 阈值随时间变化分析

在任务过程中,随着作战时间的推移,作战双方都会产生一定的火力损耗,所以编队作战体系对火力网的最低性能需求也会逐渐降低。假设火力网性能阈值随着时间的推移而逐渐减少,既Kj(t)=50-5t,在性能阈值随时间变化而变化的情况下,火力网可用度和弹性等参数随着时间和性能阈值的变化关系如图6所示。

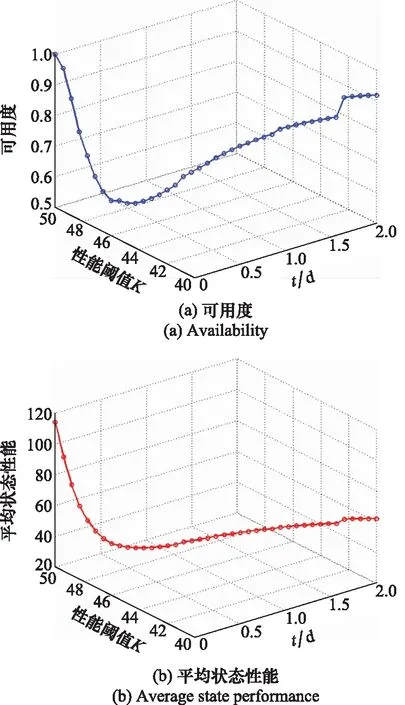
图6 不同参数随时间和性能阈值的变化

其中,火力网可用度在初始阶段下降较快,由于火力网可以进行动态重构,在当t>0.4 d时，可用度开始缓慢上升,而弹性损失量和弹性损失率在初始阶段上升较快,在当t>0.4 d时，单位时间内的弹性损失量和弹性损失率的变化逐渐趋于平稳,当t=2 d时,火力网弹性值为0.119 3。

3.2.2 动态阈值分析

当性能阈值动态变化时,编队作战体系火力网可用度和弹性等参数随时间和性能阈值的变化而变化的关系如图7所示。如图7(a)所示,火力网可用度在不同阈值的情况下变化趋势大致相同,当t=0.5 d且Kj=50时,可用度为0.457 5,当t=0.45 d且Kj=40时,可用度为0.664 31,其总体上呈现出性能阈值越大可用度越低,下降越快的趋势。如图7(c)和图7(d)所示,随着时间的推移，火力网弹性损失量逐渐增大,弹性逐渐下降,当t=0.5 d且Kj=40时,单位时间内的弹性损失量达到最大值3.692,当t=1.15 d且Kj=40时,弹性降到最低值0.171,在图7(d)中有一个平面区域,表明在该区域内的时间和阈值条件下火力网弹性保持不变。

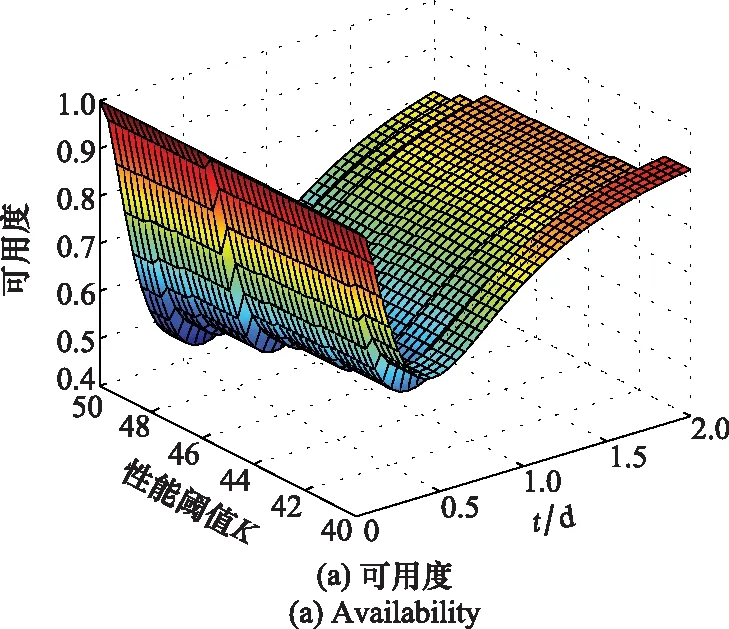
图7 不同参数随阈值动态变化关系

4 结 论

本文研究了考虑动态重构的装备体系性能层弹性及其变化规律,并以火力网的火力指数为典型性能指标为对象,根据动态双阈值多状态权重k-out-of-n系统模型开展了考虑动态重构的性能层状态变化规律及性能可用性和弹性评价方法的研究。首先,对双阈值多状态权重k-out-of-n系统模型进行动态化拓展。其次,将连续时间离散状态的Markov过程与UGF进行结合,构建考虑动态重构的火力网可用性及弹性分析模型。然后,根据建立的模型计算得出火力网及其武器系统处于不同状态下的概率和性能随时间的变化情况,并分别对性能阈值随时间变化和动态变化两种情况下的火力网可用度和弹性进行分析。分析结果表明,性能阈值越大火力网可用度下降越快,可用度越低;另外,随着时间的推移,火力网弹性损失量逐渐增大,弹性逐渐下降,且在初始阶段下降较快,然后逐渐趋于平稳。本文研究可为装备体系的可用性与弹性评价提供理论与技术指导,进而提升装备体系作战效能。