基于改进正交匹配追踪算法的属性散射中心提取

徐嘉华, 张小宽, 郑舒予1,, 宗彬锋，张敬伟

(1.空军工程大学研究生院, 陕西 西安 710051; 2.空军工程大学防空反导学院, 陕西 西安710051)

0 引 言

目前,常见的目标散射中心模型可分为理想点散射、衰减指数和模型[1-2]、几何绕射模型[3-5]和属性散射中心模型[6]。属性散射中心包含了目标的位置、形状、方向和幅度,细化了目标的后向电磁散射特征,重构雷达散射截面(radar cross section, RCS)为雷达目标识别提供了更丰富的分类识别特征[7-8]。相比于衰减指数和模型及基于几何绕射理论(geometric theory of diffraction,GTD)散射中心模型,由于属性散射中心模型增加了目标的结构参数,因此对目标电磁散射特征描述地更为精准。但随着模型参数的增加,参数估计提取的运算复杂度也随之大幅度提高。如何在确保参数估计精度的前提下,快速地提取属性散射中心模型参数成为当前散射中心提取领域研究的热点问题。

文献[9-10]提出了图像域分割估计属性散射中心参数的方法,散射中心的响应在图像中表现为多个“亮点”,即多个独立的散射中心,这一特征保证了图像分割的可行性。蒋文[11]等人提出了基于幅相分离的参数提取方法,该方法使得计算复杂度和参数估计时间降低了一个数量级。但在实际中一个散射中心的旁瓣与另一个散射中心的主瓣可能存在耦合,因此分割散射中心进行解耦合时可能存在能量泄露问题[12]。鉴于该问题的存在,李飞等人[13]运用正交匹配追踪(orthogonal matching pursuit, OMP)算法通过构建稀疏的过完备字典进行参数估计,将重构能量比提高1%解决了此类问题。段佳等人[14]在上述算法的基础上,通过模型简化、快速傅里叶变化和参数解耦提高了运算效率,迭代次数降低为原来的1/5,有效提高了算法估计效率。丛迅超等人[15]提出了基于属性散射信息的随机梯度最小方差追踪合成孔径雷达(synthetic aperture radar,SAR)超分辨重建算法,该算法提高了SAR成像分辨率,但增加了预算时间[15]。在实际提取过程中,存在信号幅度对方位向变化不敏感,OMP过程有次优解的问题。针对此类问题,提出了一种优化的OMP算法,利用过完备字典的广义正交性,直接对位置参数进行正交匹配估计,在提高了算法参数估计精度的同时大幅度降低了算法的运算复杂度。最后用仿真实验进行定性定量比较,验证了改进算法的有效性。

1 属性散射中心模型

根据几何绕射理论[16],高频区的目标散射回波可等效为多个散射中心叠加的结果,Potter等人基于此理论提出了属性散射中心模型[3],其数学表达式如下:

(1)

式中：

(2)

属性散射中心的典型目标可分为局部散射中心与分布式散射中心。其中文献[17-18]给出了常见几何体的散射中心参数。

属性散射中心模型是基于几何绕射和物理光学理论提出的一种高频区目标二维散射中心模型[6]。模型参数中包含目标物理属性和几何属性,在分析目标散射特性和雷达目标识别领域具有重要作用[7-8]。

2 属性散射中心参数提取

2.1 基于稀疏信号分析的属性散射中心提取算法

空间雷达回波具有稀疏性,可利用稀疏方法求解[9]。属性散射中心的矩阵形式表示为

s=D(θ)σ+n

(3)

式中:s表示信号回波组合;D(θ)为构建的完备字典;σ为稀疏系数向量;n为噪声。

可将原参数求解的问题转化为求解l0范数优化问题:

(4)

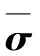
至此,由原来的参数求解问题转化为l0范数优化问题。一般采用OMP[18]对该问题求解。

2.2 OMP算法

OMP算法是一种基于迭代的贪婪追踪算法,可用于解决l0范数最小的问题,其算法步骤如下:

步骤 1输入字典D,观测信号Y和终止误差ε;

步骤 2初始化残差r1,索引集Λ0,迭代次数t.令r0=y,Λ0=φ,t=1;

步骤 3匹配寻优,令λt=argmaxj=1,2,…,N|〈rt-1,dj〉|;

步骤 4更新索引集,令Λt=Λt-1∪{λt}。

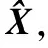
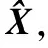
上述步骤中d表示字典D中向量。

2.3 优化OMP算法

优化算法利用了过完备字典的广义正交性,广义正交性是指:对式(3)的求解过程中,过完备字典D(θ)的内积小于10-2,可近似认为其为正交矩阵,具体步骤如下。

步骤 1构建信号Y。基于属性散射中心模型可获取目标的电磁散射回波数据,进而可构建目标的散射数据矩阵E。对仿真信号进行二维傅里叶变换后获得仿真目标的SAR图像。最后将数据从矩阵形式拉长为列向量,获得仿真数据Y。

(5)

步骤 3利用优化算法求解参数。将原问题抽象如下:

已知字典D,观测信号Y和终止误差ε。且满足DD′≈E，DX=Y。E表示单位矩阵,X为求解向量。

由DD′≈E,可得D′DX=D′Y,即X=D′Y。

选择满足误差要求的稀疏向量X作为解。

算法步骤如下:

步骤 1输入字典D,观测信号Y和终止误差ε;

步骤 2正交匹配,令MF=D′Y;

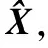
3 仿真实验

准确估计位置参数(xn,yn)将直接影响其他属性散射中心模型参数的估计精度。因此,主要针对位置参数估计这一过程进行优化,并结合传统OMP算法完成参数提取。为验证所提优化OMP算法的估计性能,从提取(xn,yn)的运算复杂度与运算时间、总均方根误差和噪声鲁棒性3个方面进行对比。仿真实验条件设置如下:雷达中心频率为9.6 GHz;信号带宽为2 GHz;方位域φ∈[-3.2°,3.2°],其他参数如表1所示,其中Sci表示散射中心i。

表1 属性散射中心参数

3.1 运算复杂度与运算时间对比

将优化后算法对属性散射中心位置参数提取过程进行优化,其余过程保持不变。计算复杂度和运算时间并仅对该过程进行对比分析。

其次，对运算时间进行比较,在不同维度、相同信噪比(signal to noise ratio, SNR)的条件下,对优化OMP算法和传统OMP算法的预算时间进行比较。分别对距离维和方位维进行维度扩展,在每个维度下进行100次蒙特卡罗实验并计算两种算法运算时间。

仿真实验1对距离维进行扩展,构建字典距离维范围取[-3.5,3.5],步长进取0.1,0.05,0.025,0.012 5。通过对比A(6 565×5 041)、B(6 565×10 011)、C(6 565×19 951)、D(6 565×39 831)4个维度下两种算法的运算时间,验证优化OMP算法的性能。实验结果如表2所示。

表2 距离维运算时间对比结果

由实验结果可知,优化OMP算法运算时间低于传统OMP算法,且维度越高,优势越明显。优化OMP算法的时间增长和维度扩展可近似为线性增长,与计算复杂度预测结果一致。

仿真实验2实验2对方位维进行扩展,方位维范围取[-3.5,3.5],步长进取0.1,0.05,0.025,0.012 5。通过对比与仿真实验一相同的4个维度下两种算法的运算时间,验证优化OMP算法的性能。实验结果如表3所示。

表3 方位维运算时间对比结果

在方位维运算时间对比实验中,传统OMP算法较距离维所用时间明显降低,但依旧高于优化OMP算法。

综合两组仿真实验,得出结论,优化OMP算法的运算复杂度和运算时间均低于传统方法,运算时间降低为原有的30%,且维度越高,降低幅度越大。

3.2 均方误差比较

为比较在不同SNR下,改进OMP算法与传统OMP算法的估计性能,在SNR为-10～0 dB下进行200次蒙特卡罗实验并比较两种算法的平均均方差(mean root mean squared error, MRMSE),其中SNR计算公式如下所示：

(6)

MRMSE定义如下所示:

(7)

(8)

(9)

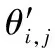
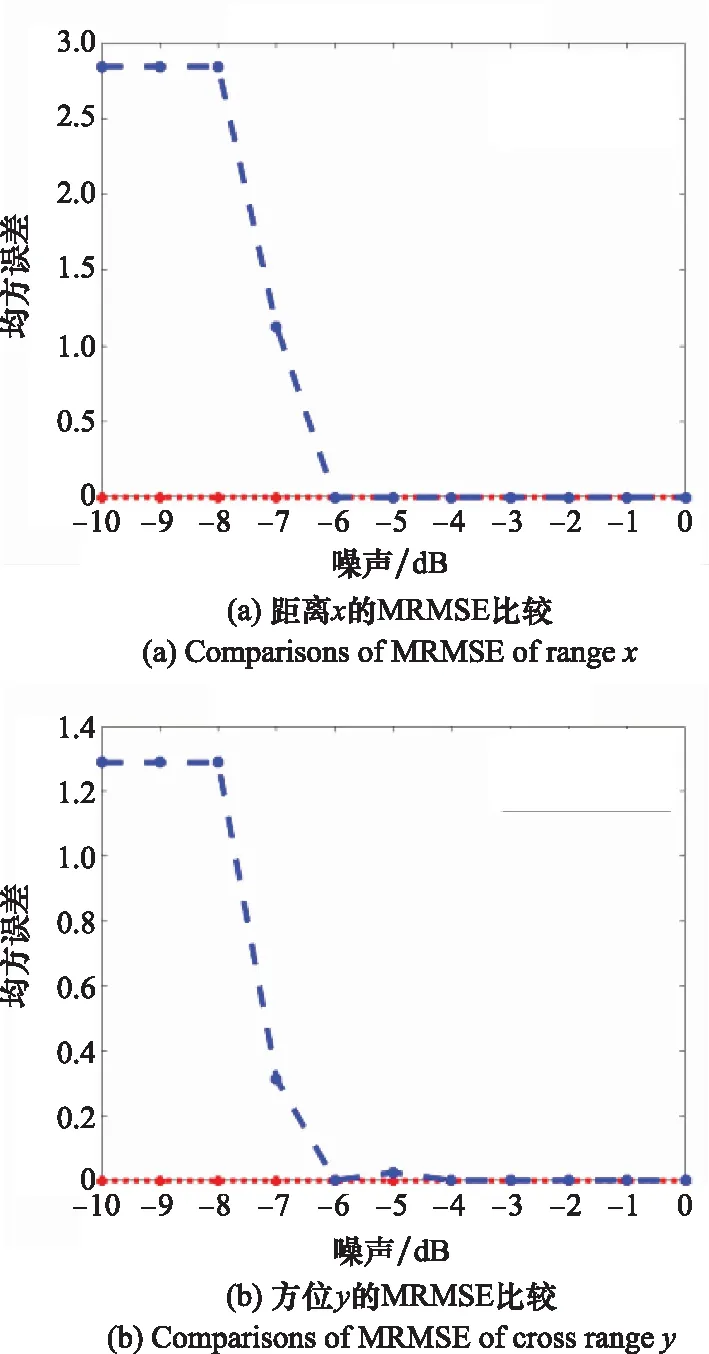
图1 MRMSE比较

3.3 噪声鲁棒性比较和RCS重构数据比较

为比较两种算法的参数估计性能,对数据重构处理并生成SAR图像,对估计性能进行直观对比。

3.3.1 数据重构

目标噪声在-10 dB时,从频率变化和方位角变化两个方面对目标重构RCS的准确度进行分析,对比两者的重构准确度。

图2为以中心频率9.6 GHz的条件下,后向RCS随方位角变化的原始值、加噪值、传统OMP算法和优化OMP算法的重构图。图3为两种算法绝对误差对比图。由仿真图可知,从方位角变化来看,优化算法在重构的准确度上具有巨大优势,除方位角0°附近的几个特别角度外,优化算法的准确度都远远高于传统OMP算法。

图2 方位向的后向RCS重构图(SNR=-10 dB)

图3 方位向重构误差对比图(SNR=-10 dB)

图4为固定方位角,后向RCS随频率变化的的原始值、加噪值、传统OMP算法和优化OMP算法的重构图,图5为两种算法的绝对误差对比图。对比结果与方位角变化基本相同,优化OMP算法的重构准确度高于传统OMP算法。与方位角变化相比,频率域RCS起伏较平缓,拟合误差小于方位角。整体而言,优化OMP算法在对RCS起伏的尖峰部分拟合效果明显优于传统OMP算法。这对增加提高目标检测概率和目标识别度有重要帮助。

图4 频率向的后向RCS重构图(SNR=-10 dB)

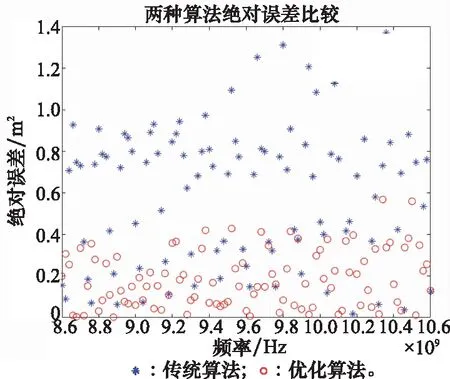
图5 频率向的重构误差对比图(SNR=-10 dB)

3.3.2 SAR成像对比

图6和图7表示在SNR分别为-10 dB和-5 dB的条件下,对数据重构生成的SAR图像进行对比,通过两组仿真对照,在SNR=-10 dB的条件下,传统OMP算法无法提取全部散射中心,而优化OMP算法仍有较好的精度;在SNR=-5 dB的条件下,两类算法的拟合精度基本相同,在噪声背景下正确提取出目标特征。SNR更低时,仿真结果同SNR=-5 dB时的实验结果相同,此处不在赘余。两组仿真结果证明了优化OMP算法在相同条件下,具有更好的鲁棒性能,可在高噪声背景下,提取目标特征。

图6 不同算法对比结果(SNR=-5 dB)

图7 不同算法对比结果(SNR=-10 dB)

两种对比均体现了优化OMP算法的在提取噪声背景下属性散射中心参数的优越性。

4 结 论

针对传统OMP算法在提取位置参数过程中运算复杂度高的问题,提出了优化OMP算法。通过理论分析运算复杂度和仿真计算运算时间,验证了优化OMP算法在运算效率的优越性。通过对比不同SNR下两种算法的均方差,得出了优化OMP算法在高SNR下,计算精度明显提升的结论。最后通过数据重构,直观地展现了优化OMP算法的噪声鲁棒性。优化OMP算法只对位置参数的提取过程进行了优化,下一步将继续研究其他参数提取的优化方法,最终将其运用于目标识别领域。