测量液体表面张力系数实验中液膜断裂点问题的讨论

方 正，王奕贤，孙锦栋，黄泽淇，张雅男，杨 迎，芮云军

(1.南京工业大学 数理科学学院，江苏 南京 211816；2.南京信息工程大学 工程训练中心，江苏 南京 210044)

液体表面存在着张力，趋向于将液体表面收缩为球形，表面张力系数是表征张力大小的重要参量. 表面张力在船舶制造、水利学、化学化工、凝聚态物理中都有广泛应用，因此测量液体表面张力系数具有重要的现实意义. 表面张力系数有很多测量方法，如拉脱法、毛细管法、滴重法、气泡法等[1-4]，其中拉脱法是通过拉升吊环下的液膜直至断裂，从而测量液体表面张力系数的方法. 现在更多采用力敏传感器实时记录吊环受力，从而计算出表面张力系数. 相比传统的约利弹簧秤，力敏传感器读数方便，测量更可靠[1]. 为了提高实验精度，人们对拉脱法实验仪器进行了很多研究，如金属丝形状、吊环的直径、拉升速度等[5-9]. 但在实验过程中，测量点的选取非常重要，关系到实验结果的精确程度以及对物理概念的理解[10-11]. 王美玉等人采用液膜拉断前电压表读数的最大值做为测量点，得到的表面张力系数误差为2.7%[12]. 郑经学等人也认为读取吊环上升过程中数字电压表显示的最大值使实验的数据测量更为准确[13]. 另一些研究者则认为最佳读数的选取点，应为断裂时瞬间的电压值，而不是拉断前出现的最大电压值[14-16]. 为什么会出现2种不同的观点？究竟选择电压“最大值”还是断裂前的“瞬间值”，大学物理实验过程中，学生常常有这样的疑问. 以拉环放置不水平，表面不干净的解释已经无法让学生信服[17-18]. 为此，笔者自制不同直径的吊环，设计实验方案，对液膜断裂点问题进行了探究.

1 理论分析

吊环从拉出液膜到液膜断裂的过程中，力敏传感器输出电压的数值经历从小变大再变小的过程[12]. 图1给出了该过程中吊环受力和液膜形状变化的示意图. 吊环脱离液面时将拉出一段液膜，此时吊环所受合外力为

F=m环g+m膜g+2fAcosθ,

(1)

式中,m膜g为液膜重力，m环g为吊环重力，fA为表面张力,由于液膜内、外表面都存在fA,所以有系数2；θ是液面与金属吊环的接触角.

随着液面高度逐渐下降，吊环拉出的液膜(m膜g)变多，θ则减小，由式(1)可知，吊环拉力F变大，直至达到最大Fmax，此时θ=0[图1(b)]，有

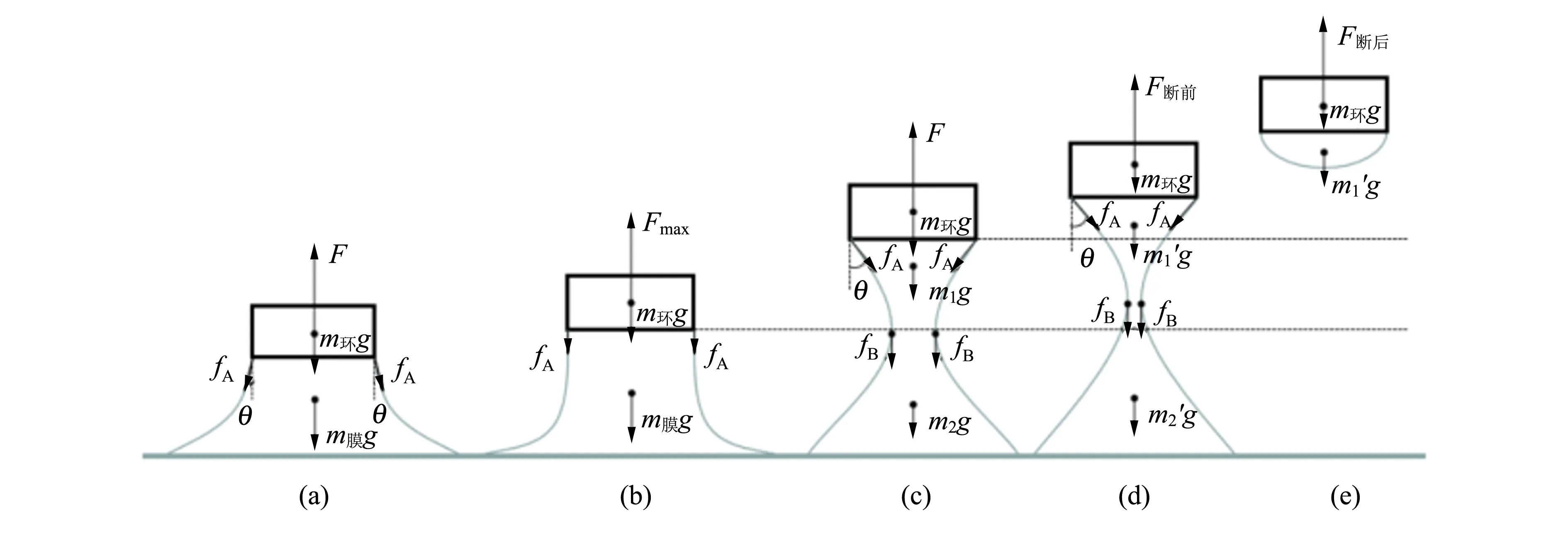
图1 液膜拉伸过程示意图

Fmax=m环g+m膜g+2fA,

(2)

继续下降液面高度，在重力和分子内聚力的作用下，液膜的体积和形状将发生显著变化，液膜剖面从鞍面型逐渐变成双曲面型[图1(c)][15].内、外2个双曲面的顶点处液膜将逐渐变薄，直至液膜断裂[图1(d)].为了便于分析，将拉出的液膜质量分成m1和m2上下2部分.将吊环与上半部分液膜(m1)作为整体，该整体受到的表面张力，作用点在液膜最薄处，表示为fB，如图1(c)所示.很显然，液膜变薄过程中，fB保持不变，作用力的方向也始终竖直向下，但是上半部分液膜质量将从m1逐渐减小到m1′，所以吊环拉力F也渐渐减小.在断裂瞬间[图1(d)]，有

F断前=m环g+m1′g+2fB,

(3)

此时的液膜m1′将停留在吊环上，如图1(e)所示.所以拉断后，吊环所受拉力为吊环重力与残留液膜重力之和.

F断后=m环g+m1′g,

(4)

很显然，对比式(3)和(4)，液膜断裂前、后的拉力之差为2fB，这正是液膜断裂点的表面张力，计算出的表面张力系数是准确的.同样，对比式(2)和(4)，吊环拉力之差为2fA+(m膜-m1′)g，此差值中除了有表面张力外，还包含一部分液膜重力，所以计算出的表面张力系数数值将明显偏大.因此文献中普遍采用液膜断裂点来计算表面张力系数[14-16].

值得注意的是，图1(c)中的fA表示液体与金属环接触处附近的表面张力，fB表示液膜最薄处的表面张力，两者都是液体在空气界面处的表面张力，所以fA=fB.采用整体法，将吊环与m1整体作为研究对象，fB为该整体受到竖直向下的外力，而fA则为内力，无论其角度θ如何变化，与吊环拉力F无关.

由此，表面张力f用电压来表示，为

f=F断前-F断后=(U断前-U断后)/K，

(5)

2 实验结果与讨论

2.1 基于Umax与U断前的表面张力系数比较

表1 采用电压最大值和水膜断裂瞬间值计算得到的表面张力系数及其误差

图2 实验设备

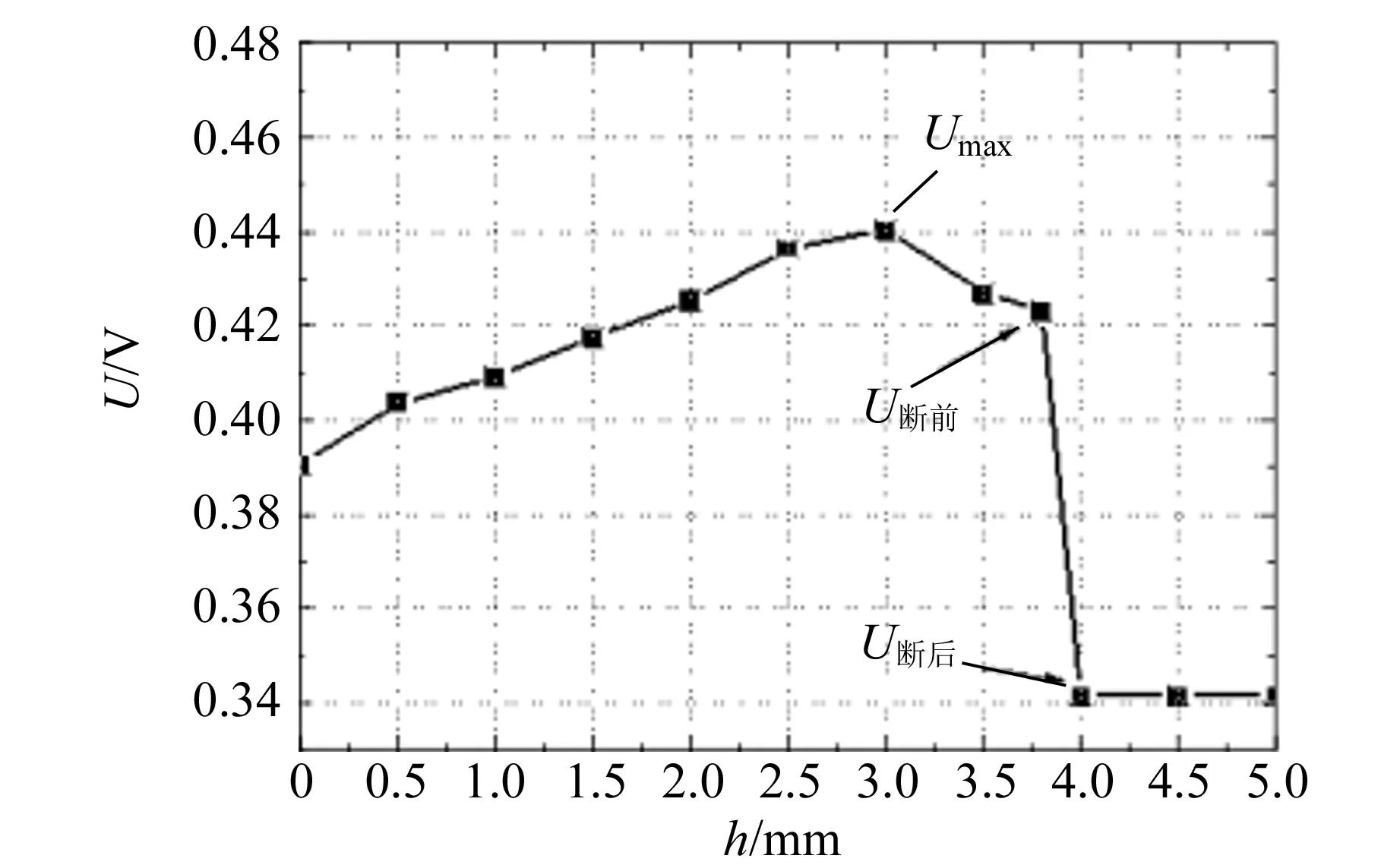
图3 水膜拉升高度与传感器电压值之间的关系

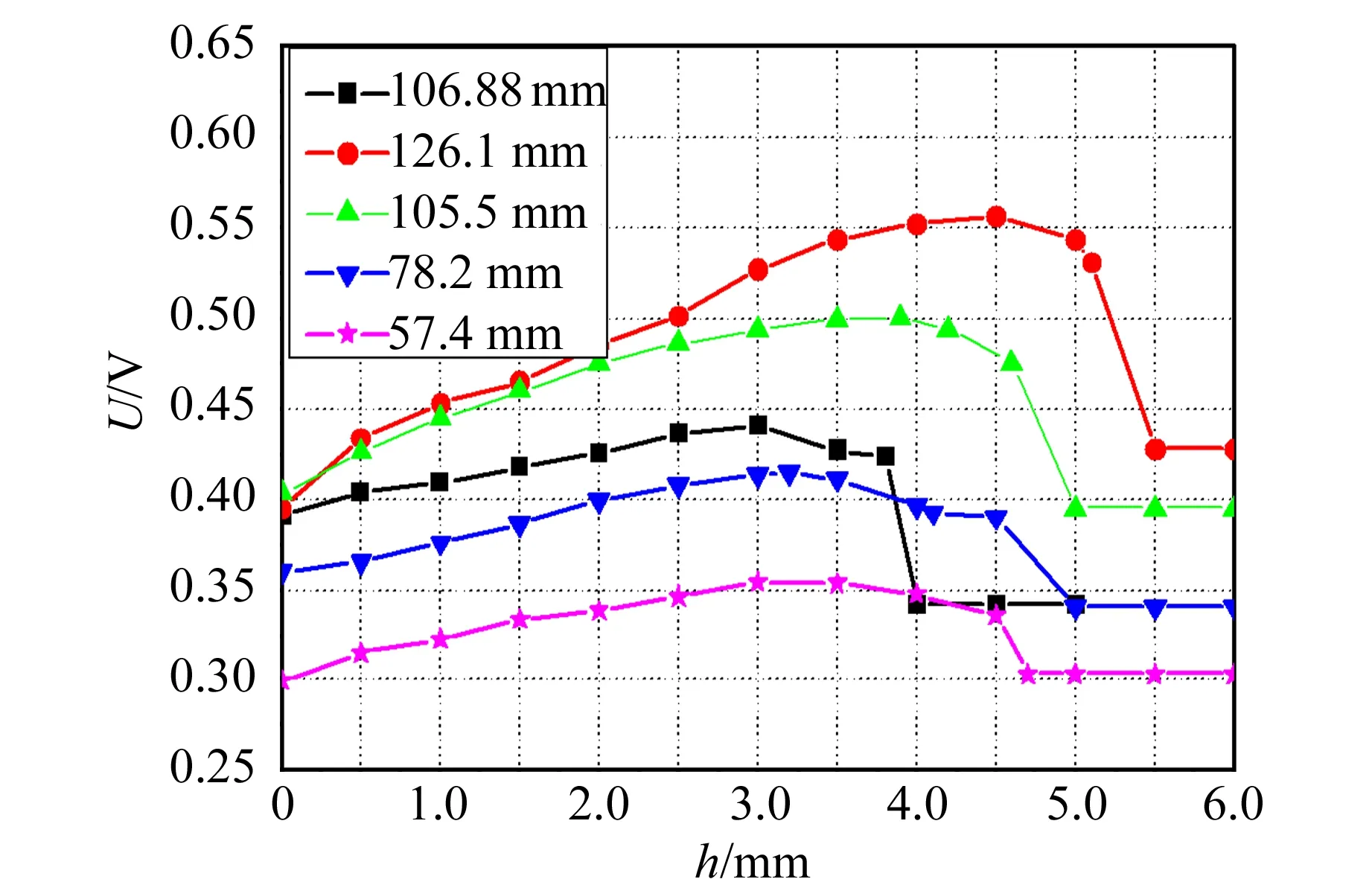
图4 5个吊环拉升水膜的高度与电压值的关系

对于标准环，可以发现，采用电压最大值计算得到的表面张力系数α1=87.2×10-3N/m，与标准值相对偏差为19.4%. 而采用水膜断裂瞬间值计算得到的α2=72.0×10-3N/m，相对偏差仅为-1.4%，两者差别非常大. 电压最大值计算得到的水的表面张力系数，比采用水膜断裂瞬间值计算得到的数值大很多，即α1>α2. 对于其他不同周长的圆环也都有相同的结论. 即如前面理论分析所述，是由于(m膜-m1′)g所致，这里得到了实验验证. 所以，正如多数文献中提到的，采用断裂点计算得到的α2更加接近标准值，误差更小[14-18].

2.2 基于U断前的表面张力系数修正

实验发现，采用断裂点计算的表面张力系数α2，随着吊环周长的减小而不断减小.对于126.1 mm周长的吊环，得到α2=76.7×10-3N/m，对于57.4 mm周长的吊环，α2=53.3×10-3N/m，表面张力系数减小了约1/3.表面张力系数的测量值是否与吊环尺寸有关？笔者因此对实验测量进行更为系统的研究[7-8].

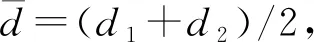
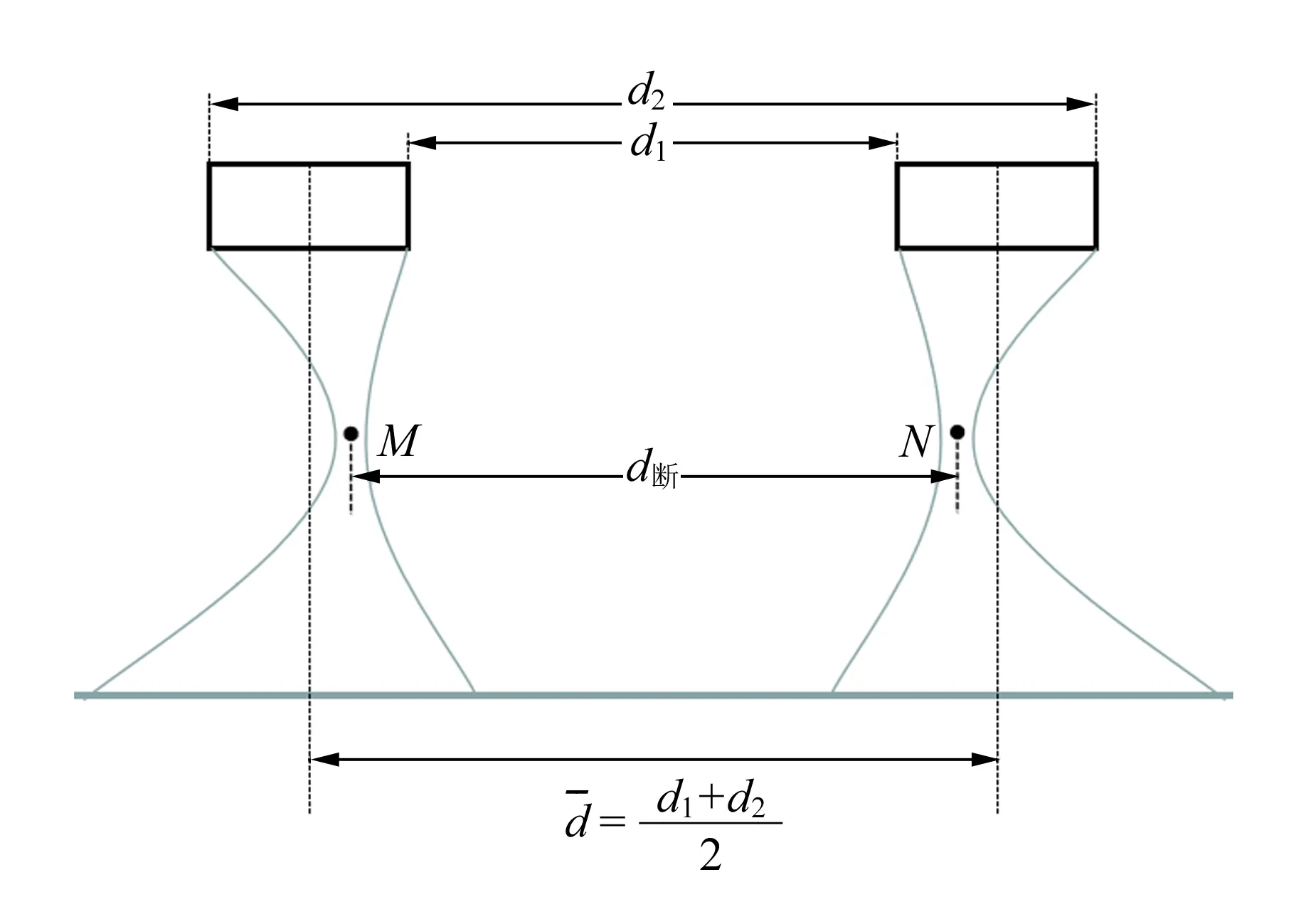
图5 水膜直径变小示意图

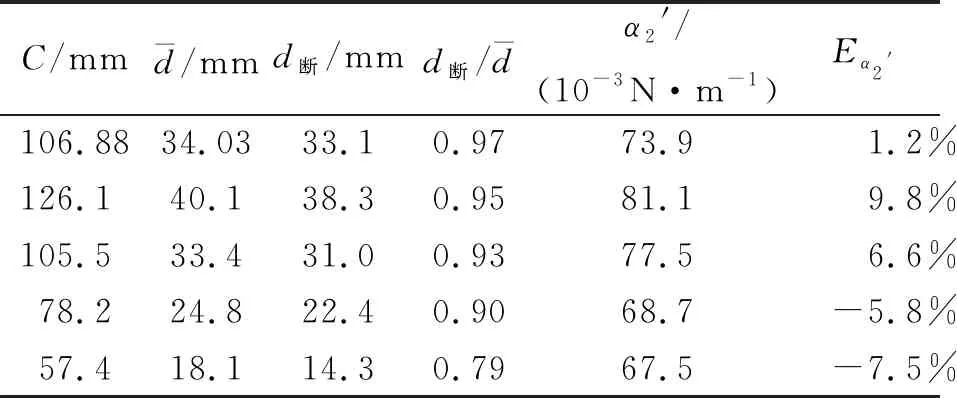
表2 环直径与水膜断裂处直径的比较以及修正后的表面张力系数

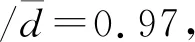
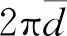
(a)水膜断裂照片

2.3 基于Umax表面张力系数的修正

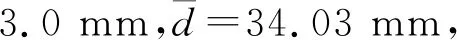
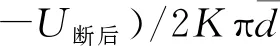
(6)

计算，由表3可以看出，除了最小吊环，相对误差仍为-4.5%外，其他自制吊环测量的表面张力系数的相对误差都小于4.0%.

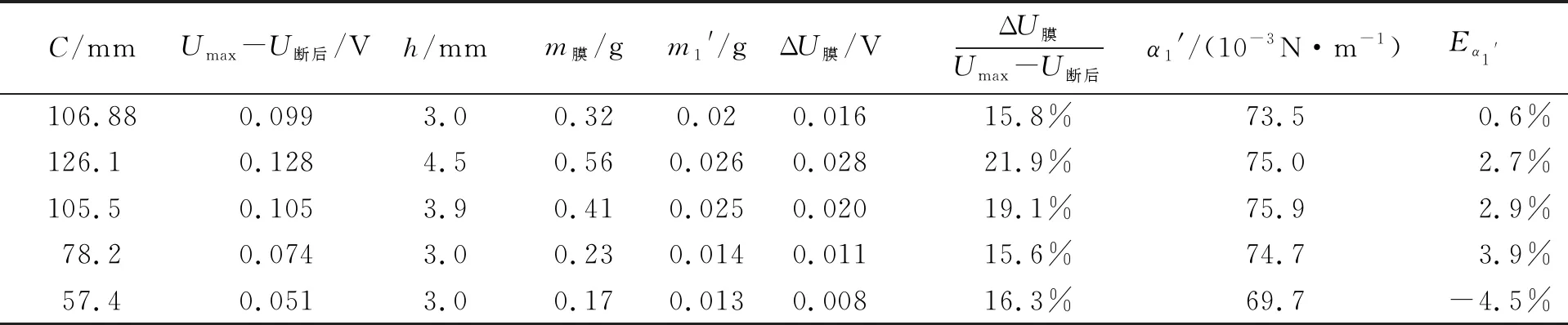
表3 考虑水膜重力用最大电压处修正后的表面张力系数

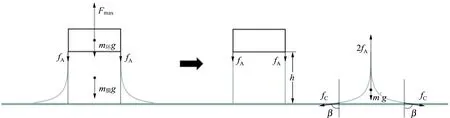
图7 最大电压处水膜受力分析图

3 结束语

本文讨论了表面张力系数测定中的液膜断裂点问题. 通过完整的液膜拉升过程的受力分析和实验验证，找到误差来源. 对电压最大值点，必须考虑液膜自身重力，由此得到的表面张力系数修正值与理论值的误差较小. 对于液膜断裂的瞬间值，则必须考虑液膜断裂处的直径收缩，从而对表面张力系数也要进行修正. 虽然此时液膜受力的物理图像清晰，但是由于实际操作中，断裂点的电压读数非常困难，所得结果误差较大.