基于纳米压痕的木材细胞壁力学测量值与加载载荷相关性研究
2021-07-27蔡绍祥李延军黄燕萍郭玉良
蔡绍祥,李延军,黄燕萍,郭玉良*
(1. 常熟理工学院纺织服装与设计学院,江苏 常熟 215500;2. 南京林业大学材料科学与工程学院,南京 210037;3. 南通理工学院建筑工程学院,江苏 南通 226007)
近年来随着纳米压痕技术应用于木材微观力学的研究,实现了在亚微米水平下直接测量木材细胞壁的弹性模量、硬度和黏弹性性质。Zhang等[1]和Meng等[2]采用该技术研究静态恒定应力作用下木材细胞壁的蠕变性能,以及动态载荷交变应力作用下木材细胞壁的力学滞后现象和损耗等微观力学特性。Gind1等[3]研究了杉木的细胞壁微观力学性能与其纤丝角以及木质素含量之间的关系,结果显示,其弹性模量和微纤丝角负相关,而硬度与木质素含量以及纤丝角无显著相关性。Tze等[4]运用多次卸载的方法测量了火炬松(PinustaedaL.)的弹性模量和硬度与压入深度的关系。在这些微观力学性能的测试过程中,因为加载载荷和探针位移都在高分辨率下,易受仪器精度、测试方法、测试环境变化和操作等诸多因素影响,理论模型和试验测试时的加载参数都会直接影响样品的试验结果。以上影响因素会导致测试数据不稳定,对材料微观力学性能测试结果的有效性产生不利影响。因此,在木材科学领域应用纳米压痕技术需要开展在应用过程中的试验参数标准化研究,规范试验测试过程,确保测试数据的可靠性和一致性。不同材料所用最大加载载荷不一致,大部分学者[5-7]开展对针叶材细胞壁研究时,加载力为250 μN;Li等[8]研究竹材时采用400 μN加载力;廖承斌[9]研究荻草微观力学性能时的加载力为150 μN;刘嘉新等[10]研究昆虫鞘羽采用的是10 mN加载力;葛俊[11]研究牙釉质和骨采用1 000 μN加载力。初步试验表明,加载速率对试验结果有一定影响,这与宏观力学方面有类似情况,不同加载速率时所测得的木材力学性能也是不一致的[12]。自20世纪80年代末以来,以纳米压痕测试蠕变行为的4种主要试验方法包括恒定位移试验法、恒定载荷速率试验法、恒定应变速率试验法、恒定载荷试验法[13]。在各种压痕测试蠕变行为的方法中,目前最常见的是恒定载荷试验法,此方法中,在恒定的加载载荷下进行保载停留,并监测保载时探针压痕深度的增加。在恒定保载载荷情况下记录位移变化,此阶段还可以计算出保载阶段应力的变化。
此外,材料的密度、硬度以及压痕深度对测试结果影响也很大,不同材料在测试过程中选取的加载载荷也不一样。因此,探求木材细胞壁在纳米压痕过程中合适的加载载荷、加载时间和保载时间对测试结果的准确性至关重要:首先要确立整个试验过程中的测试标准参数;另一方面,在黏弹性性能研究时,所选择的应力水平必须满足“小于材料线性黏弹区域的临界应变值”这一前提条件,以确保试验在线性黏弹区域内进行。因此,在研究木材细胞壁黏弹性性能时,要计算出试验产生的应力大小,使应力大小在线性黏弹性区域内。笔者采用南方分布最为广泛的马尾松为研究对象,研究在纳米压痕试验时应该采用的载荷函数参数和加载载荷,为研究其静态和动态力学性能提供参数标准。
1 材料与方法
1.1 试验材料
试验用材选自福建南平国有林场,位于26°15′~28°19′N、117°00′~119°17′E。采集林为人工林马尾松(PinusmassonianaLamb),树龄40 a,马尾松树高20.15 m,1~9 m位置平均直径32.8 cm。采集地为海拔100 m的低丘陵,年均气温19.50 ℃,年均降雨量1 600~2 000 mm,年均相对湿度80%~84%。为了使试验结果准确性更高,需要控制样品选择过程,选择相同高度、年轮和早晚材部位,减少因微纤丝角和化学成分差异而产生的试验数据变化。试验样品制作方法为:在树高1 m处取厚度为25 mm的圆盘,然后在圆盘上沿南北向过髓心,沿径向取一个宽为10 mm的木条,从木条成熟材区(30轮处)取晚材部分,并制作尺寸为5 mm(弦向)×5 mm(径向)×10 mm(纵向)的小木块。采用滑走切片机制作一端为四棱锥形的小木块样品,样品的锥形横切面作为试验需要抛光的平面。用滑走切片机对试样进行抛光的过程中,首先用玻璃刀将锥形端刨出宽约为1 mm的光滑平面,然后用钻石刀再次进行刨切,使得表面光滑平整,表面粗糙度小于10 nm,目视界面有镜面反射效果为止。样品在测试前要进行含水率平衡处理,即在相对湿度65%、温度20 ℃的恒温恒湿箱内存放1周。
1.2 仪器与设备
截锯机、微型加压夹具、干燥箱、木材滑走切片机(A-1170,Wien-Austria)、玻璃刀、钻石刀、超薄切片机(Leica Inc., Germany)、纳米压痕仪(Hysitron, Inc.)和恒温恒湿箱(HWS-1000型)等。纳米压痕仪的测试系统主要包括样品测试平台(sample stage)、光学显微镜观察定位系统(optics system)以及力学传感系统。纳米压痕仪载荷和位移分辨率分别为1 μN和0.01 nm,试验中使用的是金刚石Berkovich探针,针尖曲率半径30 nm。
1.3 试验方法与表征
1.3.1 试验方法
1)测定区域和测试点选择。利用纳米压痕仪内部光学显微镜观察样品表面,每个样品测试5个细胞。通过纳米压痕仪扫描探针显微镜(SPM)技术扫描木材细胞壁,发现其结构较清晰,如图1a所示,其中,探针扫描三维效果图1c所示,反映的是探针扫描细胞壁时的受力大小分布关系。
2)测试操作。在本试验中采用加载-保载-卸载三段式加载曲线,使得材料在保载过程中产生蠕变;同时,保载阶段获得的蠕变信息可以作为研究木材黏弹性的重要依据。试验完成后,探针会在细胞壁S2层上留下痕迹,一般每个细胞壁选择20个点进行压痕。为验证探针压痕是否在S2层上,需要再次扫描,扫描后获得的痕迹信息如图1b所示。

图1 纳米压痕探针扫描图示
1.3.2 黏弹性表征
纳米压痕加载曲线仍为三段式(恒速率加载、保载、恒速率卸载),可获得材料在不同加载载荷、加载时间和保载时间条件下的蠕变行为。具体测试过程:加载和保载时间均为5 s时,加载载荷分别为100,150,200,250,300,350,400 μN。根据试验结果,以纳米压痕-木材流变学理论计算微观蠕变的相关参数,并探讨其与加载载荷、加载时间和保载时间等因子的关系。因此,试验中采用纳米压痕技术对木材细胞壁蠕变特性进行了研究,获取黏弹性相关性能。
加载载荷对蠕变位移有影响,为更直观比较保载阶段蠕变位移量的大小,可直接计算其蠕变率。因此,在探讨木材细胞壁蠕变性能,以及不同加载载荷对蠕变性能的影响时,采用纳米压痕的保载阶段蠕变率进行表征。蠕变率(CIT)定义为压痕深度的相对变化比率,在保载阶段所施加的载荷保持不变,计算公式如下[14]:
(1)
式中:h2为保载阶段末段的最终穿透深度;h1为加载段末段的穿透深度,如图2所示。

图2 不同加载载荷-位移曲线
纳米压痕过程中瞬时应变位移速率表示为:
(2)
式中:h为压头探针瞬时穿透深度;t为加载时间。
压痕过程中应变率(ε1)的计算公式为[15]:
(3)
式中,ht为蠕变过程中监测的压头位移。
蠕变过程中的应力变化[σ(t)]计算公式为[16]:
(4)
式中:Ac(t)为圆锥针尖与测试物接触面积随时间变化的函数;Pmax是加载最大载荷。
Ac(t)可近似根据探针尖端接触面积函数计算:
(5)
式中:Ci为探针尖端常数参数(试验设备自带软件提供参数值);hc为探针接触深度。
1.3.3 幂次律
所有基于纳米压痕方法分析蠕变数据时都要使用基本方程进行计算。纳米压痕仪探针压入时的应力从在探针尖端附近的比较高到离尖端较远区域的极小值,应力水平存在梯度变化。一般选择最大应力作为计算过程中的特征应力(或有效应力),通常需要在模型中进行计算,与定义弹性模量和硬度的计算过程类似。选择一个特征应力作为蠕变分析的特征值重要参数,即Mulhearn等[17]研究成果中使用的计算方程。Bower等[18]的计算也验证了这一观点,在较低应力作用下,蠕变速率与应力在双对数坐标下呈线性关系,即蠕变行为的应力相关性可以用幂次律来表达:
(6)
2 结果与分析
2.1 加载载荷对弹性模量和硬度的影响
试验中使用的Berkovich压针针头曲率半径小于100 nm,取准静态的恒速率加卸载模式。最大载荷分别为100,150,200,250,300,350,400 μN,加载时间为5 s,达到最大载荷后继续保载5 s,然后通过仪器自带软件自动得出材料的弹性模量和硬度等数据。压痕过程包括4个阶段:第1阶段为探针逼近阶段,逼近速率为10 nm/s;第2阶段为探针压入阶段,当针尖接触到样品表面时,以50 μN/s的恒定加载速率压入样品,达到设定的最大载荷(Pmax);第3阶段为最大载荷保持阶段,保载时间为5 s;第四阶段为卸压阶段,卸载时间为5 s。在整个加载过程中的不同载荷-位移曲线见图2。
整个试验过程由加载、保载和卸载3个阶段组成。试验完毕后观察测试后的压痕位置,从所有压痕点中选择20个有效数据样本进行分析,然后计算出加载载荷分别为100,150,200,250,300,350,400 μN时的硬度和弹性模量,计算结果见图3。结合试验数据分析可知,细胞壁弹性模量在载荷为350 μN时达到最大,在200~350 μN时弹性模量相对稳定,变化不大;当加载载荷达到350 μN时,弹性模量开始下降。加载载荷从100 μN增加到400 μN时,不同载荷时弹性模量平均值最大相差17%,可见加载载荷的变化对弹性模量有较大影响。计算得到的弹性模量不能直接作为材料的弹性模量,Oliver等[19]认为测得的弹性模量应为探针和样品系统的弹性模量,也称为复合响应模量,其与样品和探针的弹性模量、泊松比之间存在一定关系。木材泊松比是常数,木材细胞壁弹性模量的计算与加载载荷和探针接触面积直接相关,因此,加载载荷变化会引起弹性模量测量值的变化。

图3 不同加载载荷下细胞壁弹性模量和硬度
纳米压痕测试数据也受到探针压痕深度的影响,弹性模量和硬度随压痕深度(面积)的变化而变化。这在低硬度材料中更明显,在各向同性材料中也会发生,尤其是晶体材料[20]。压痕深度变化被归因于与样品抛光质量、测试工件(压头探针角度和探针/表面摩擦)和材料性能有关[21]。材料压痕深度引起的这种变化可以从压痕探针与木材细胞壁的接触面积来解释,载荷越小,压痕深度越小,接触面积就越小,从而影响弹性模量和硬度的大小。利用纳米压痕连续测量技术测量木材细胞壁弹性模量,计算结果表明,压痕深度为0~100 nm时弹性模量随压痕深度增加而增加,压痕深度大于100 nm后其弹性模量趋于稳定[4]。
通过试验测量得到的硬度随加载载荷增加而小幅升高,最大变化为10%左右,排除误差影响,加载载荷在100~400 μN时对硬度测量值影响有限。根据Oliver等[19]的方法可知,测得的硬度与加载载荷成正比,与压痕深度的平方成反比。对于同一种材料,加载载荷越大,压痕深度就越深。加载载荷的变化和压痕深度的变化密切相关,并共同影响硬度的测量值,通过试验数据求得的硬度变化较小。Kollmann等[22]对280种木材的硬度进行了试验测试,结果显示,木材硬度只与其屈服应力相关,试验过程中加载的载荷对硬度影响有限。根据Fischer-Cripps[23]的经验公式H=CY(H为木材细胞壁硬度,C为材料屈服系数,Y为材料的压缩屈服应力),硬度与材料屈服或压缩流动应力的大小成正比。因此,当探针所施加的压力达到材料所受的压缩屈服应力后,细胞壁硬度不再增大,保持相对稳定。本研究过程中,硬度测试值变化规律符合其理论预测结果。Oliver等[19]也发现纳米压痕试验过程中,探针的位移变化在一定范围内,随着探针压入深度的增加,深度与弹性模量变得更加具有线性相关性。当探针压入一定深度后,其弹性模量才相对稳定。此外,使用纳米压痕连续测量技术可以较好地表示样品的硬度或弹性模量在压痕深度为100~200 nm时的值,其弹性模量随深度的增加而缓慢变大,直到200 nm时弹性模量保持相对稳定,而硬度则变化较小[4]。
2.2 加载载荷对蠕变性能的影响
首先分别采用的最大载荷为100,150,200,250,300,350,400 μN,从图2中可知总的压痕深度和蠕变阶段的蠕变量都随载荷增加而逐渐变大。根据软件输出的相关数据可计算此阶段的蠕变量和蠕变率,从数据分析可知,卸载后的压痕残余深度也不一样,随着载荷的增大压痕残余深度逐渐变大。由试验中扫描出的压痕残余深度图像可以看出,压痕凹陷随最大加载载荷增大而逐步加深。由软件中记录的数据分析可知,纵向残余深度约占总深度的70%,弹性恢复只占总变形的30%,这表明此时细胞壁S2层的变形以塑性变形为主。不同加载载荷下的蠕变率见图4,由图4可知,蠕变率随加载载荷的增加逐渐变大,即当载荷由100 μN增加到400 μN时,蠕变率增加了73%。

图4 不同加载载荷下的蠕变率
蠕变现象是压痕试验中常见的现象,常被认为是一个需要解决的问题。Chudoba等[24]研究了如何在测量硬度和模量时消除蠕变,研究指出,蠕变效应有时会导致卸载初期压头深度的净增加和载荷的减少。这是因为Oliver等[19]对弹性模量和硬度测量的分析主要集中在荷载降低时的初始阶段深度递减率上,为避免在弹性模量和硬度测量中出现此类误差,Chudoba等[24]建议在开始卸载前,将最大载荷保持一段时间。保载停顿的目的是让材料蠕变,即充分变形,使蠕变变形在卸载过程中不再显著。这一基本原理所固有的概念是,蠕变率将随时间延长而下降。由于加载载荷和压痕深度在纳米压痕过程中可以连续监测,因此可以收集关于保载阶段蠕变行为的信息,并通过相关试验解释这些现象,从而获得蠕变性能的相关参数。而要获得较为准确的木材细胞壁弹性模量和硬度测量值,其蠕变率不能过大,否则蠕变率过大会引起木材细胞壁结构的破坏,从而影响木材细胞壁的弹性模量和硬度。因此,在确定试验过程中的加载载荷时,并不是加载载荷越大越好。利用纳米压痕测试材料的蠕变性能常用的方法为:稳态蠕变、固定深度法、恒速加载法、恒定压痕应变速率法。根据相关研究数据表明,纳米压痕过程中采用恒载法是较为可靠的描述材料蠕变性能的方法。由于压痕探针是锥形体,在恒定载荷的初始阶段压入细胞壁速度较快;随着时间的延长,探针与木材细胞壁接触面积更大,所受阻力更大,从而延缓了蠕变时间。
2.2.1 加载载荷对应变率和蠕变应力的影响
当逐渐增加加载载荷时,在保载阶段蠕变位移随时间的变化情况如图5所示。为保证试验数据的有效性和可靠性,需增加测试细胞个数和压痕次数。每个数据是20~25个有效测试点的平均值,并且使标准偏差控制在数据平均值的5%以内。压痕深度为80~200 nm,该压痕深度对于木材是较为合适的,一方面克服了表面的尺寸效应,另一方面也不会因为太深而破坏细胞壁的结构。对于不同的载荷,可以很清楚地分辨出压入深度的不同,为后续的讨论提供了参考。由图5可知,压痕深度随着加载载荷的增加逐步增加,最大增加幅度达140%,因此,载荷对压痕深度影响显著。

图5 不同载荷下保载阶段压痕深度变化曲线
公式(4)和(5)的计算结果如图6a所示。在保载阶段,蠕变应力随着时间的延长缓慢减小,减小的幅度平均为17%,这是因为接触面积也是随着时间延长而逐渐增加的。不同载荷条件下,在蠕变初始阶段,应力减小较明显,而随着蠕变时间的增加,应力减小的幅度变小。这种两段式的变化从应变率(图6b)中可以更明显地观察出来,应变率在6 s时迅速降低,此后几乎保持不变。但是在应变率图中,不同载荷的区分并不明显。从图6b中可以观察到蠕变变化情况分为2个阶段:首先是初始阶段,此时为应变速率迅速减小阶段,这一阶段源于材料本身的瞬态效应,也同样受到加载过程探针与细胞壁接触面积的影响;其次是相对稳定阶段,当蠕变速率维持在稳定值时可反映材料的长程行为,是材料抵抗变形能力的体现。两段式的变化规律从应变和蠕变率的变化趋势图中可反映出来。根据试验数据研究表明:在一定载荷范围内蠕变性能是线性行为;超过一定载荷时,木材纵向压痕蠕变性能是非线性行为,其应变率与蠕变应力相关,两者可以通过幂次律进行描述。不同载荷下瞬时应变位移速率变化如图6c所示。由图6c可知,每个试验的缩进位移率在9 s后趋于恒定,表明了这些缩进的保持步骤消除了大部分细胞壁的蠕变成分。探针在压入一定深度后,一方面克服了表面尺寸效应对试验结果的影响,同时也不会因为压痕深度过深而破坏细胞壁的结构。本研究中的载荷范围可刚好保证探针在一定范围内实现对细胞壁黏弹性性能的有效测试。
图6b可直观地反映蠕变的实时变化。在保载阶段不同加载载荷下,蠕变过程中应变率曲线呈现不同结果。由图6b可知,试验中蠕变阶段的蠕变位移速率在5 s后趋于稳定,在保载的初始阶段蠕变位移增加较快,而在后期蠕变位移增加趋于稳定,增加量很小。Xing等[25]研究发现,不同的载荷导致木材细胞壁的应变率不同;还发现在不同加载载荷作用下,蠕变在加载5 s后应变率明显降低。进一步证明在加载阶段其应变率较大,且随时间延长下降迅速;在保载阶段(5~10 s)应变率下降缓慢,保载的初始阶段应变率下降较保载后期更快。Li等[26]在研究改性的木材细胞壁静态黏弹性时发现,细胞壁在纳米压痕不同阶段应变率变化曲线不同,且保载阶段细胞壁应变率变化较小。本研究中的细胞壁应变率在纳米压痕的保载阶段变化也较为平稳,说明该加载载荷大小符合要求,细胞壁所受蠕变应力变化较小,细胞壁结构未被破坏。因此,可以利用幂次律关系探讨应变率和蠕变应力的相关性。
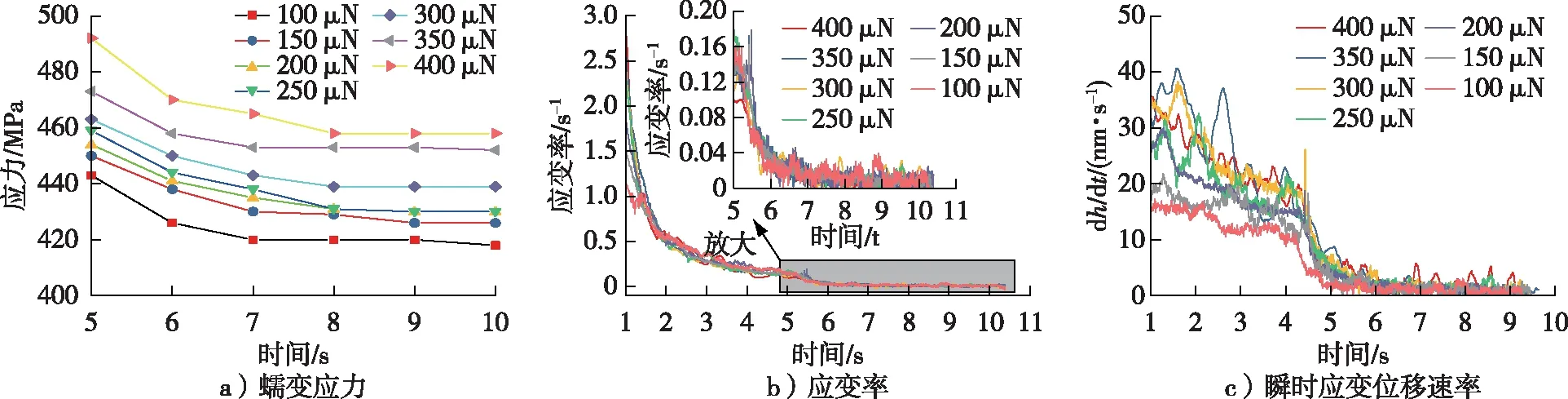
图6 不同载荷下蠕变应力、应变率和瞬时应变位移速率随时间变化的曲线
2.2.2 应变率和蠕变应力的幂次律关系
蠕变阶段的参数对材料的长期利用是重要的考察参数,计算建立的各载荷作用下蠕变阶段(5~10 s)应力和应变率平均值的木材细胞壁幂次律关系。应变率(蠕变阶段的蠕变速率)与应力(蠕变阶段的应力)已计算过,此处将10 s时的应力和应变率进行平均,得到一个代表性的应力和应变率对数坐标值,如表1所示。由于10 s处是保载阶段蠕变的最后阶段,如果此位置在线性黏弹性范围内,则5~10 s都应在线性黏弹性范围内。不同载荷对应的蠕变应力、应变率以及线性拟合结果如图7所示,在对数坐标下使用线性拟合,得到的应力因子n≈1。结合拟合图形中试验数据与拟合曲线之间的关系可以看出,对于马尾松木材,在应力为420~460 MPa时,非线性较弱,近似可以认为是线性黏弹性行为。结合拟合曲线,可以判断对应的加载载荷为150~300 μN时为线性黏弹性变形,试验数据具有较高可靠性。研究不同加载载荷对弹性模量和硬度的影响时发现,加载载荷为200 μN时弹性模量达到最大值,结合需要在线性黏弹性范围内进行试验,在对马尾松木材细胞壁进行纳米压痕时合适的加载载荷为200~300 μN。

表1 幂次律在不同载荷下10 s时的对数坐标值

图7 不同载荷对应的蠕变应力、应变率以及线性拟合结果
3 结 论
利用纳米压痕仪测试马尾松木材细胞壁时,通过改变纳米压痕过程中的加载载荷大小,研究加载载荷与木材细胞壁弹性模量、硬度和蠕变性能之间的关系,并探求在线性黏弹性范围内合适的加载载荷。
1)加载载荷分别为100,150,200,250,300,350,400 μN时,马尾松木材细胞壁弹性模量变化明显。当载荷为200 μN时,弹性模量达到最大值,随后保持相对稳定;改变加载载荷时,测得的木材细胞壁硬度随载荷的增加而变大。
2)蠕变率随着加载载荷的增加而逐渐增加,蠕变阶段的应变率和蠕变应力都具有二段式变化趋势,第1阶段在4~6 s时变化较大,第2阶段在7~10 s时变化平缓。
3)根据试验数据,并利用幂次律进行分析可知,加载力为150~300 μN时可近似认为是线性黏弹性行为;结合加载载荷变化对弹性模量和硬度的影响,可以判断在对马尾松之类的针叶材进行纳米压痕试验时,合适的加载载荷为200~300 μN。
