相对论量子体系的相空间规范变换

王怀玉

(清华大学 物理系， 北京 100084)

0 引言

在文献[1]中，给出了量子体系的相空间规范变换。就是对于坐标和动量做一个尺度变换，尺度变换因子α>0，而体系的能量谱保持不变。因此这个变换的特点是保能量的。该规范变换是适用于薛定谔方程的。也就是在低动量运动时的规范变换。

本文将相空间规范变换推广到狭义相对论的情形。我们发现，在狭义相对论的情况，为了继续保能量，光速常数需要做一个与坐标一样的尺度变换。

1 相对论相空间的规范变换

在文献[1]中，当一个粒子服从量子力学的薛定谔方程

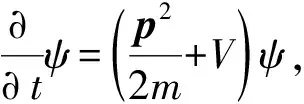
(1)

可以对于坐标和动量做如下的尺度变换，

r→r/α=r′,p→pα=p′

(2)

我们此处用黑斜体表示矢量。它们可以是一维、二维和三维空间中的量。做了这样的变换后，只要哈密顿量中的参量做相应的尺度变换，则哈密顿量的形式保持不变。相应地，能量本征值谱保持不变。所以说，这样的变换是保能量谱的。

文献[1]给出了两个典型的粒子体系。一个是简谐振子模型，其哈密顿量是

(3)

注意，其中势能项已经按照文献[1]那样，写成一个弹性系数k的形式。对此哈密顿量做式(2)的尺度变换，相当于质量和弹性系数做如下的变换，

m→mα2=m′,k→kα2=k′

(4)

哈密顿量(3)式就成为

(5)

可见，式(3)哈密顿量的形式保持不变。因而，本征波函数和本征值的形式也保持不变。由于频率ω并未变化，说明能谱也没有变化。因此，这个变换是保能量的。

另一个例子是氢原子势。哈密顿量为

(6)

除了做(2)的变换，同时令

e2→e2/α=e′2

(7)

那么，哈密顿量(6)就成为

(8)

哈密顿量的形式就保持不变。由于本征能量的表达式中含有因子me4，因此也是保能量的。

我们现在要把式(2)的这种尺度变换推广到狭义相对论的情况。

在狭义相对论中，时空坐标构成四维矢量。不同惯性参照系的四维矢量之间是通过洛伦兹变换相联系的。本文所涉及的是两个基本的四维量：时空坐标和四维能量-动量。

x=(r,ict),p=(p,iE/c)

(9)

首先想到的是，四维量如三维量一样，按照式(2)做尺度变换。即对式(2)添加时间和能量分量即可。经过尝试，我们发现不是这样的。

现在我们把相对论量子力学方程写下来。它们是自旋为0的克莱因-高登方程

(10)

和自旋为1/2的狄拉克方程。

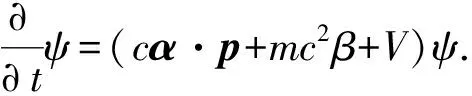
(11)

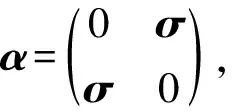
先考虑自由粒子的情况，即在上两式中，令势能V=0.我们立即可以看到，除了做式(2)的尺度变换之外，还要对于光速常数做如下的尺度变换：

c→c/α=c′.

(12)

如此，自由粒子的哈密顿量的形式可以保持不变。注意，既然现在是保能量的变换，哈密顿量就应该保持不变，相应地，时间变量也不需要做变换。这一点与作者前面的预想不一样。我们注意到，将变换式(2)和(12)应用于(9)式的四维量，

x→(r/α,i(c/α)t)=(r′,ic′t)=x′，p→(pα,iEα/c)=(p′,iE/c′)=p′

(13)

时间和能量确实就不需要做变换了。反过来，由于时间不做尺度变换，因此，速度与坐标具有同样尺度变换。此处对于式(13)中的四维矢量要有一个说明。空时四维矢量x的第四个分量如果称为时间分量，是不确切的。真正的时间是t。空时矢量的第四个分量是ict。同理，动量能量四维矢量的第四个分量iE/c不是真正的能量，能量是E。

以下以氢原子和谐振子模型为例进行讨论。

对于氢原子势，狄拉克哈密顿量是

(14)

做式(2)、(4)、(7)和(12)的尺度变换之后，哈密顿量的形式保持不变。狄拉克方程求解氢原子的问题，在量子力学教科书上有介绍[2]。此处就不叙述了。我们只是提到一点，在氢原子的本征能级的表达式中，有一个重要的常数：精细结构常数,记为αs.它的表达式为

(15)

在式(7)和(12)的尺度变换下，精细结构常数也保持不变。这是因为，精细结构常数在这儿的作用是表示能级劈裂。既然整个能谱是在相空间规范变换下不变的，表示能级劈裂的精细结构常数当然也不应该变换。

我们再来讨论谐振子模型。

一般说来，在薛定谔方程中的势能是V，那么，在狄拉克方程中的势能保持不变。例如，在薛定谔哈密顿量中是库仑势(6)式，在狄拉克哈密顿量中是加在对角元上的同样的库仑势，见式(14)。可是谐振子的情况有所不同。

早在1978年，就有人考虑过相对论谐振子的问题[3]。1989年，Moshinsky和Szczepaniak基于狄拉克方程，提出了三维相对论性谐振子的模型[4]。他们就把这个模型称为狄拉克谐振子。随后，文献[5-8]专门研究了这个模型。在文献[9]中有较为详细的介绍。三维狄拉克谐振子模型出现之后，自然地，有人给出了相应的一维和二维狄拉克谐振子模型{10-11}。本文为简便起见，只讨论一维狄拉克谐振子。二维和三维的情况同此讨论，只是表达式更为繁琐。

一维狄拉克哈密顿量如下

(16)

狄拉克谐振子哈密顿量(16)式的一个特点是，代表势的项是加在非对角元上的，所以是一个矢量势，而不是加在对角元上的标量势。这就是前面所说的，相对论性的谐振子势与一般的势能不同之处。

对于式(10)做式(2)、(4)和(12)的尺度变换之后，哈密顿量的形式保持不变。而且，其中频率ω不参与变换。

本征值中的正能量支是

(17)

相应的归一化本征波函数是

(18)

其中ψn(x)是归一化的谐振子本征函数。两个分量的下标量子数刚好差1。两个分量的系数如下，

(19)

我们看到，经过尺度变换(4)和(12)式，能谱(17)式是不变的。而且系数a1和a2也保持不变。

最后我们简单提一下二维和三维狄拉克谐振子。

二维狄拉克谐振子的哈密顿量为

(20)

正的能量本征值为

(21)

三维狄拉克谐振子的哈密顿量为

H=cα·(p-imωβr)+βmc2

(22)

三维空间中，除了自旋角动量，还有轨道角动量。求解得到的正能量本征值是

(23)

其中，l=0,1,2,…;j=l+1/2.由于总角动量是轨道角动量与自旋角动量之和，总角动量量子数总是半整数，因而j+1/2总是整数。

二维和三维狄拉克谐振子哈密顿量都是在式(2)、(4)和(12)的尺度变换之后，其形式保持不变，它们的本征函数也具有(18)和(19)式的形式。

2 讨论

对于薛定谔量子体系的尺度变换[1]，为了保能量不变，除了对于坐标和动量做式(2)的尺度变换，还需要对其它的量特别是对物理常数的尺度变换。例如对于质量的变换(4)式和对于单位电荷的变换(7)式。在相对论量子力学体系中，还要加上对光速c这个物理常数的变换(12)式。在[1]中未涉及到对于c的变换，是因为如下的原因。

一个相对论自由粒子的能量是

(24)

文献[1]中只考虑了薛定谔方程的情况，也就是粒子做低动量运动。它的动能就是将(24)式做展开后再减去静止能量。

(25)

由于根号只展开至一级项，所以这个动能的表达式中，不出现光速。因此，文献[1]中未涉及对于光速的尺度变换。如果将根号展开至二级项，

(26)

那么，在动能的表达式中，光速常数就显现出来。就会涉及光速的尺度变换式(12)。因为二级项体现了相对论修正，所以就必然涉及光速常数。

不过，普朗克常数ћ是不做尺度变换的。这一点，反映了量子力学的特征性。因为其它的量，如电荷、光速等，经典力学中也有这样的量。当取经典极限时，量子力学的尺度变换自然过渡到对应的经典力学的尺度变换，尽管后者可能不是保能量的。但是普朗克常数ћ是经典力学所没有的。如果ћ也做尺度变换，那么，当过渡到经典力学时，必须取ћ→0.从而ћ的变换在经典力学就消失了，这个变换在经典力学中就没有对应物，这会引起矛盾。因此，为了不导致矛盾，普朗克常数ћ不能做尺度变换。这也表明，无论空间如何在尺度变换下伸缩，能量量子是不变的。这也与保能量变换这一特点相一致。

上一节我们只讨论狄拉克方程了。本文未对克莱因-高登方程做讨论，因为讨论是类似的，没有新的内容。

在相对论量子力学中，并不是式(9)的四维矢量都做尺度变换，而只是空间的三维矢量做变换，时间和能量不做变换。这相当于低速或者静止的粒子的状态。确实，文献[1]和本文所举的体系，例如氢原子和谐振子模型，哈密顿量都与时间无关，都是计算定态薛定谔方程。

狭义相对论的时空坐标符合洛伦兹变换。粒子在运动时，沿运动方向的空间会有收缩，看到的一个物体会有旋转后的效果。

狭义相对论中粒子在运动时，由于洛伦兹变换所感受到的空间的压缩与空间尺度变换相比，各有特点。狭义相对论中，粒子运动时，只感受到沿着运动方向上的空间的压缩而没有膨胀；压缩的程度在不同的点是不一样的，而且其中涉及到时间的因素；在垂直于运动方向上的空间尺度不变。相空间尺度变换时，空间各点既可以有压缩也可以膨胀，这取决于比例因子α的数值；在空间的所有维度上都有压缩或者膨胀；空间各点的压缩 或者膨胀的比例是完全相同的，且与时间无关。

如果势能是含时间的，那么，时间也就不得不做尺度变换。相应地，能量也就必须做尺度变换。那时，就不能保证这样的尺度变换是保能量的。所以，本文讨论的空间尺度变换，只适用于粒子静止或低动量运动的体系。

3 结论

(1) 本文把量子体系的相空间规范变换推广到相对论情形。在相对论情况下相空间规范变换是r→r/α,p→pα再加上光速常数的变换c→c/α=c′.时间和能量不做变换。因此，仍然是保能量的。

(2) 相空间规范变换有效的前提是，哈密顿量与时间无关。如果哈密顿量与时间有关，那么，为了保持哈密顿量在尺度变换下保持不变，时间就不可避免地也要做变换。相应地，能量也必须做变换。就不能实现保能量。在做尺度变换时，单位电荷和光速常数等一些物理常数也会做相应的变换。但是普朗克常数不做变换。原因是，普朗克常数只在量子力学中出现，而在经典力学中没有这个量。