基于有限元极限平衡法的建筑荷载对土质边坡稳定性影响分析

2021-07-27段鹏宇

华北科技学院学报 2021年3期

段鹏宇

(河北地质大学地球科学学院，河北石家庄 050031)

0 引言

边坡失稳主要是在外界不利因素影响下触发的[1]。这些不利影响因素导致边坡土体剪应力增加或抗剪强度降低，使土体抗滑力小于下滑力从而造成边坡失稳发生滑动[2-3]。随着社会经济的发展，越来越多的建筑修建在边坡顶部，因此造成的土质边坡失稳导致的工程事故问题愈发严重，已严重影响到了人民群众的生命财产安全。进行建筑荷载条件下边坡稳定性研究对指导安全施工，避免土质边坡失稳具有重要意义。

边坡稳定性分析经过数十年的理论和实践研究，其研究分析方法已发展较为成熟。目前，研究分析边坡稳定性的确定性方法主要有极限平衡法(Limit Equilibrium Method,LEM)[4-5]和有限元分析法(Finite Element Method,FEM)[6-7]。但是，这两种方法在应用上都存在一定局限性：LEM基于静力平衡理论，只能对边坡稳定性状态进行宏观的判断，不能对边坡土体的应力和应变特征进行全面分析，因此适用于均质土边坡，不适用于地层岩性复杂的边坡；FEM引入变形协调的本构关系使得其理论更加严谨，不需要事先假定破坏面的位置或形状，并且可以通过边坡的应力应变变化来分析边坡的变形破坏过程，但是FEM不能给出明确的边坡稳定系数和滑动面。

单一的LEM或FEM都不能对边坡进行全面的稳定性分析，因此本次研究采用FEM和LEM相耦合的有限元极限平衡法(Finite Element Method - Limit Equilibrium Method，FEM-LEM)对建筑荷载条件下边坡稳定性进行分析。将计算得到的有限元应力导入到传统的极限平衡分析，每一个单元应力已知，可以计算出每个条块底部中点的正应力和下滑剪应力，每个土条的下滑力和抗滑力都求出来以后，把这些力在滑动面上积分，就可以求出边坡稳定系数。应用FEM-LEM不仅可以通过边坡土体的应力应变分布来分析边坡变形，还能用计算得出的稳定系数对边坡稳定性进行宏观判断。本文以一个建筑荷载条件下均质双层土边坡为例，应用FEM-LEM和LEM对其进行稳定性分析，并计算出建筑物距离坡顶边缘的安全距离，为今后此类工程问题提供借鉴。

1 基本原理

1.1 弹塑性理论

对于弹塑性体[8]，应力增量和应变增量的联系如下：

{dσ}=[D]ep{dε}

(1)

式中，[D]ep为弹塑性矩阵，且：

[D]ep=[D]-[D]p

(2)

(3)

式中，[D]为弹性矩阵，F与Q分别为塑性屈服函数和塑性势函数。对于关联流动，F=Q；对于理想塑性材料，A=0。

1.2 屈服准则

采用Mohr-Coulomb屈服准则[9]，其屈服函数为：

(4)

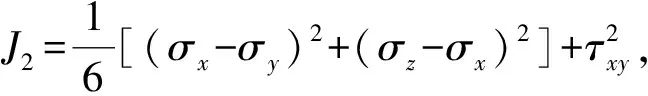
当θ=0°及θ=60°时，代入式(4)分别得：

(5)

(6)

由式(5)，(6)得：

(7)

(8)

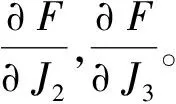
1.3 边坡稳定系数

由有限元分析可得剖分网格每个单元高斯积分点的σx，σy和τxy，可以得到单元中任一点的应力值。将潜在滑面划分为若干土条，根据土条底部中点坐标值，通过应力张量变换，可以得到土条底部正应力和剪应力，通过对所有土条的下滑力和抗滑力积分求和得到滑面总下滑力和总抗滑力。边坡稳定系数[10]定义为：

(9)

式中，li为土条长度；σi为土条底部中心正应力；τi为土条底部中心剪应力；ci为土条粘聚力；φi为土条内摩擦角。

2 建模与计算

2.1 边坡概况

以一典型土质边坡为例，来分析建筑荷载条件下边坡稳定性。边坡分为两层，上层土厚度5 m，下层土厚9 m，坡高为10 m，边坡比为1∶1.5(竖向：水平)。将建筑物自重对边坡的作用力看作均布荷载，以三层建筑物为例，根据《建筑结构荷载规范》(GB 50009-2012)相关要求计算，坡顶建筑物对基础的作用力分别为30 kPa、60 kPa、90 kPa、120 kPa和150 kPa(分别对应一层楼、两层楼…五层楼建筑对基础的作用力)，作用范围为8 m。各层土体的物理力学参数如表1所示，边坡示意图如图1所示。

表1 各层土体物理力学参数

图1 边坡示意图

2.2 初始状态分析

(1) 建立模型

采用GeoStudio软件对该边坡未加建筑荷载的初始状态进行稳定性分析，利用SIGMA/W模块将边坡进行有限元划分，网格间距1.5 m，划分网格大多为四边形，少数为三角形。整个计算模型划分为441节点，386单元。边坡有限元计算模型如图2所示。

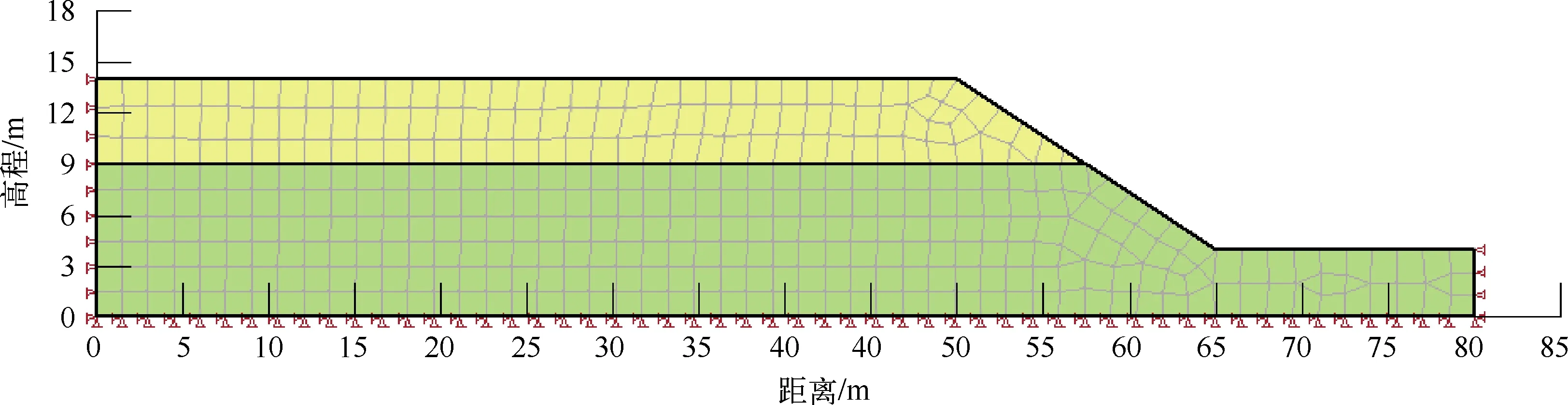
图2 初始状态边坡有限元计算模型示意图

模型边界条件为：左右两侧水平方向(X方向)位移为0，竖直方向(Y方向)自由；底部水平和竖直方向位移均为0。

(2) 有限元边坡稳定性计算

将SIGMA/W模块和SLOPE/W模块耦合计算边坡稳定性，利用FEM-LEM计算得到边坡最危险滑动面示意图(如图3所示)。由图3可知边坡在天然条件下稳定系数为1.460，边坡处于稳定状态。

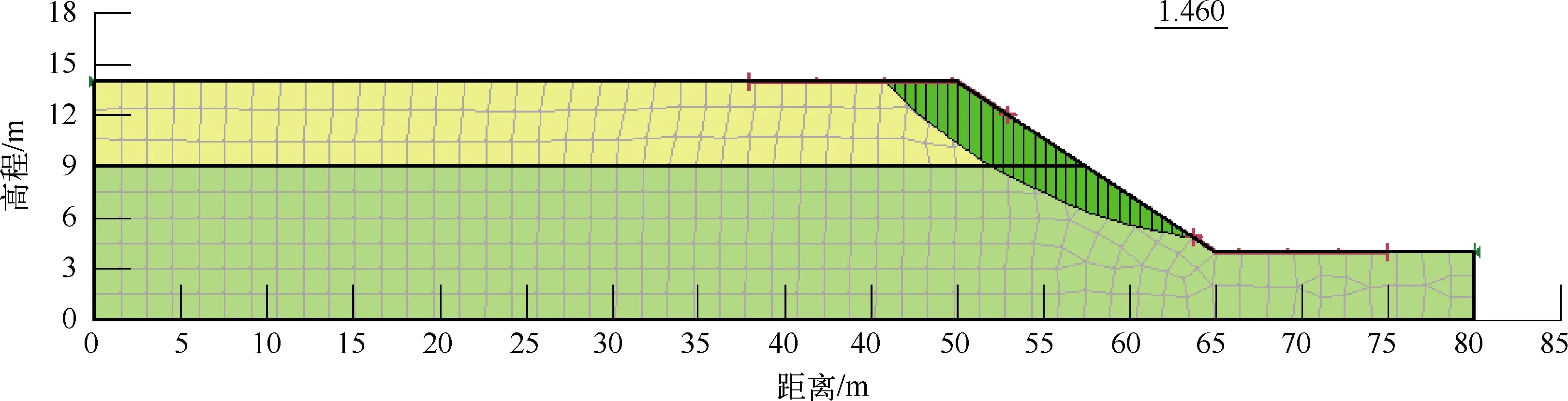
图3 边坡最危险滑动面示意图

(3) 与传统LEM计算结果比较

为和LEM应用效果进行对比分析，采用相同的土体物理力学参数通过多种LEM对边坡进行稳定性计算，稳定系数计算结果和与FEM-LEM计算结果的差值百分比见表2，其中Morgenstern-Price法计算得出的最危险滑动面如图4所示，其条块基底法向应力与FEM-LEM计算的出的条块基底法向应力对比曲线如图5所示。

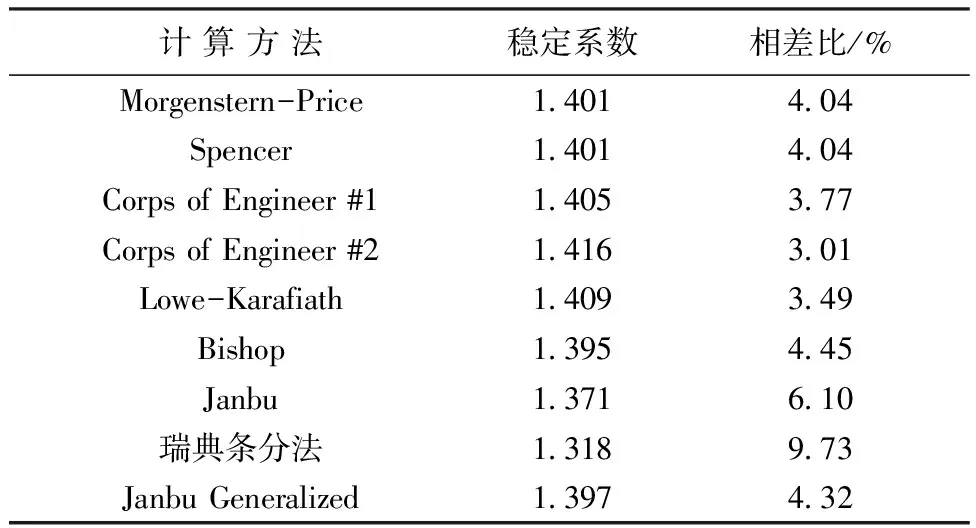
表2 各种LEM计算所得最小边坡稳定系数

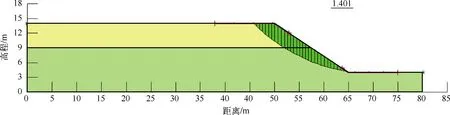
图4 Morgenstern-Price法计算所得最危险滑面

① 稳定系数比较：由表2可知，各种LEM的计算结果都比FEM-LEM的计算结果小。文献[11，12]的研究成果也证实了这个结论。9种LEM中，普通条分法的相差较大，为9.10%。其他8种方法的稳定系数计算结果相近，与FEM-LEM计算结果相差小于4%。说明利用FEM-LEM计算边坡稳定系数是可行的。各种LEM计算结果不同是因为各种LEM的静力平衡和条间力的假设不同，其中瑞典条分法不考虑条间力，计算结果偏差较大。FEM-LEM计算了土体真实的应力，并将其带入LEM中求解稳定系数，减少了条分法各种假定带来的误差，计算结果更加符合实际情况。

② 最危险滑动面比较：由图3和图4可以看出，FEM-LEM和Morgenstern-Price法计算得到的滑面位置不相同。由图5可知，滑面中部至下部FEM-LEM和LEM的法向应力分布差异显著，而在坡脚处FEM-LEM的法向应力集中明显，这是因为LEM土条基底法向应力是由土条重量提供的，因此LEM体现不了真实的坡体应力。这也是LEM的一个局限性。

图5 边坡滑面土条法向应力

2.3 荷载状态下分析

对边坡进行建筑荷载条件下稳定性分析，网格与初始状态下的网格剖分一致，底部和左右两侧边界条件不变，建筑物对地基的作用力分别为30 kPa、60 kPa、90 kPa、120 kPa和150 kPa(分别对应一层楼、两层楼…五层楼建筑对基础的作用力)，计算模型示意图如图6所示。建筑荷载和建筑物至坡顶距离对边坡稳定性有重要影响，为分析影响因素对边坡稳定性的影响程度，在距离坡顶处0-12 m范围内，基于FEM-LEM计算得到不同建筑荷载和建筑物至坡顶距离对应的边坡稳定系数见表3，并对建筑荷载、建筑物至坡顶距离和边坡稳定系数进行皮尔逊相关性分析，分析结果见表4。

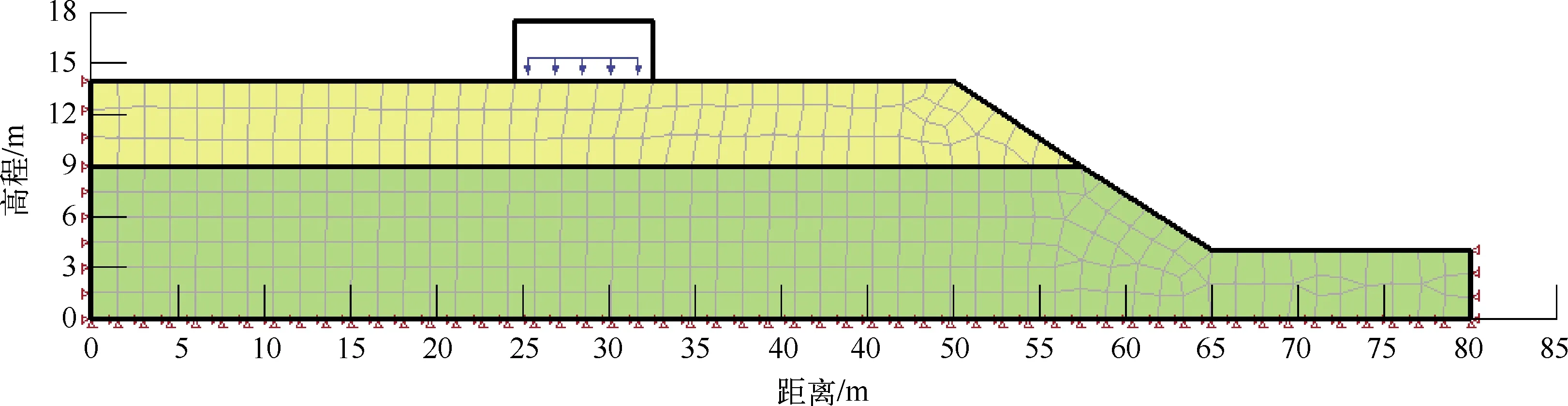
图6 荷载条件下计算模型示意图

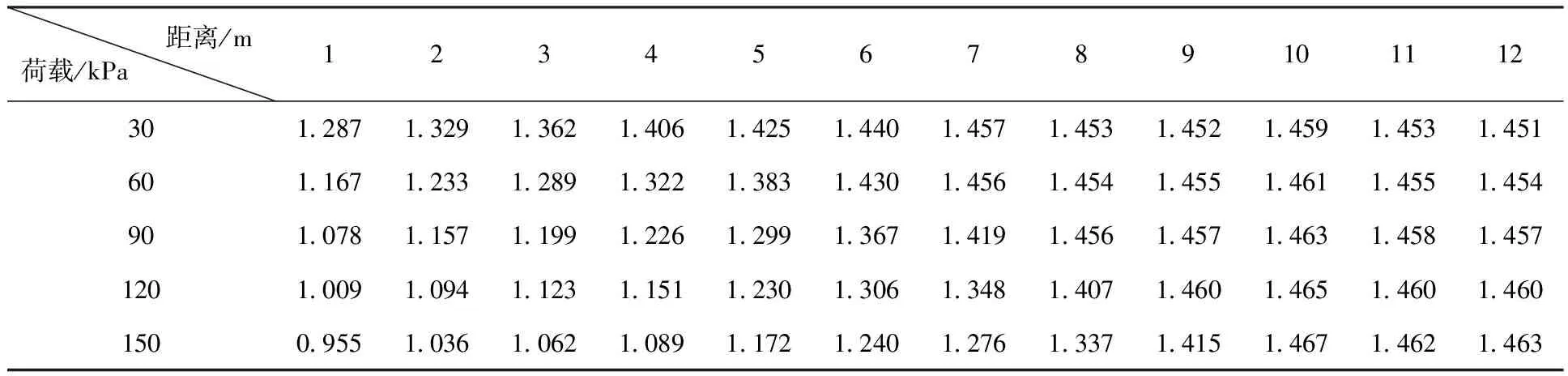
表3 不同荷载及建筑距离下边坡稳定系数

表4 皮尔逊相关性分析表

由表4可知，荷载与边坡稳定系数间相关性的显著性为0.001小于0.005，表示两者之间相关性显著，两者间的相关系数为-0.411，表示荷载值和边坡稳定系数之间是负相关。建筑物至坡顶距离与边坡稳定系数间相关性的显著性为0，表示二者之间存在显著的相关关系，相关系数为0.815表明建筑物至坡顶距离与边坡稳定系数相关性显著，两者为正相关关系。由表3可知，随着建筑物至坡顶距离的增大，边坡稳定系数增大，边坡稳定性增强，但建筑物至坡顶距离到达一定值之后，边坡稳定程度不再发生改变。

根据《建筑边坡工程技术规范》(GB 50330-2013)相关要求，该边坡属于二级边坡，边坡安全系数为1.30。利用FE-LEM经逐步计算，得到荷载30 kPa、60 kPa、90 kPa、120 kPa和150 kPa下建筑物至坡顶最小安全距离，分别为1.2 m、3.2 m、5.05 m、5.92 m和7.4 m。以荷载120 kPa为例，得出最小安全建筑距离下边坡稳定系数如图7所示，边坡位移矢量图如图8所示。

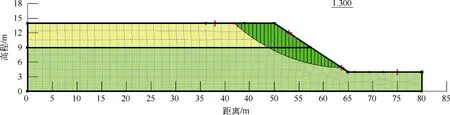
图7 有限元计算所得建筑荷载条件下边坡稳定系数

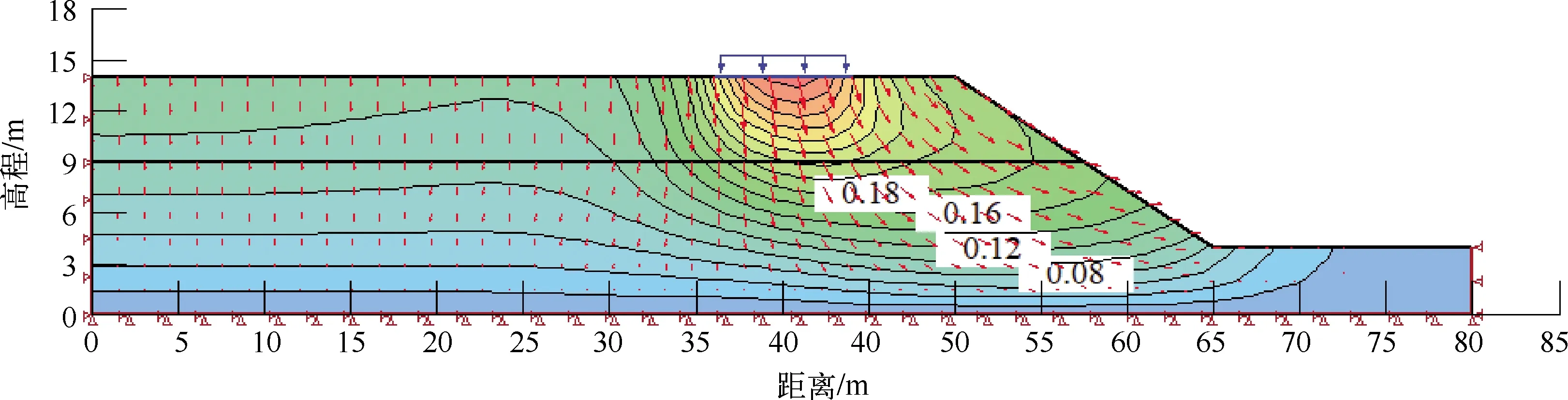
图8 有限元计算所得边坡位移矢量图

由图7和图8可知，建筑荷载120 kPa下边坡稳定系数为1.30时，边坡坡面最大位移量为0.18 m，坡脚位移量为0.08 m。根据表3可知，建筑物至坡顶距离为9 m到更大时，边坡稳定系数变化幅度很小，边坡稳定状态基本不变。因此建筑荷载为120 kPa(四层楼)时，建议建筑物距离坡顶安全距离为5.92～9.0 m。同理，建筑层数为1时，建筑物至坡顶距离建议为1.2～7.0 m；建筑层数为2时，建筑物至坡顶距离建议为3.2～7.0 m；建筑层数为3时，建筑物至坡顶距离建议为5.05～8.0 m；建筑层数为5时，建筑物至坡顶距离建议为7.4～10.0 m；将FEM与LEM相结合来分析边坡稳定性，既能考虑坡体变形对边坡稳定性的影响，又可以得出稳定系数来评价边坡稳定性，可以对实际工程边坡进行全面分析。