矿井涌水量回归模型预测方法研究
2021-07-27张润畦蒋知廷
姚 辉,张润畦,蒋知廷,刘 鑫
(华北科技学院 河北省矿井灾害防治重点实验室,北京 东燕郊 065201)
0 引言
矿井涌水量是在矿井建设和开采过程中,单位时间内通过各种途径涌入井巷的水量[1],其指标大小是制定合理开采方案、选用合理排放水设施的依据[2]。如果短时间内矿井涌水量超出矿井排放水设施负荷,将会导致煤矿透水事故的发生,造成人员伤亡和财产损失。因此,对矿井涌水量的预测将直接影响到矿井建设安全。
随着生产技术的飞速发展,涌水量预测方法也在进行着革新。从传统意义上纯粹的利用数学公式进行推导——大井法及水文地质比拟法,到后来融入了计算机模拟技术的数值法,再到现在融合了数理统计及计算机分析的各种不确定性分析方法的提出——BP神经网络[3]、灰色系统理论[4],预测方法呈现形式多样化的变化趋势。但综合来看,矿井涌水量是受各种因素共同影响的结果,抛开矿井现有生产资料所造成的影响去进行涌水量分析显然过于片面,预测精度会降低很多[5]。
本文以时间序列季节加法模型为基础,以河南某矿近20年月度平均涌水量数据为研究对象,综合考虑上述分析方法中未曾考虑到的季节因素及不确定性因素,建立起涌水量预测模型,以期实现矿井涌水量预测精度的提升。
1 理论基础
时间序列是研究对象中某一变量按照时间排序形成的数值序列。通过对变量在一定时期内的变化过程进行研究,可以得到该研究对象的演变规律及趋势,从而预测其未来走向[6,7]。
1.1 ARIMA(p,d,q)模型
自回归移动平均模型(ARIMA)是自回归模型(AR)及移动平均模型(MA)的综合形式[8],通过差分手段,将非平稳时间序列准平稳化后再建立起ARIMA(p,d,q)模型[9]。其中p为自回归阶数,d为序列平稳化所采用的差分阶数,q为移动平均阶数。
当p,d,q已知时,ARIMA的数学表示形式[10]为
(1)
式中,yt为t时刻y的预测值;φ为自回归系数;θ为移动平均系数;μ为常数;ζ为t时刻的误差。
1.2 季节分解模型
一般来讲,时间序列有4种主要影响因素分别是:Tt,长期趋势,表示序列值随时间变化所展现的长期发展趋势;St,季节趋势,表示因季节性因素而呈现的规律性变化;Ct,循环趋势,表示序列值循环变动;It,不规则变动,表示剔除其他因素后剩余的随机波动[11,12]。
其数学表达式为
yt=f(Tt,St,Ct,It)
(2)
f函数表示模型的加法和乘法运算。
2 实证分析
选取河南某煤矿2000年~2020年的月度涌水量数据,将2000年~2019年的数据作为分析处理数据,将2020上半年的数据作为检验数据。
原始数据如表1所示。
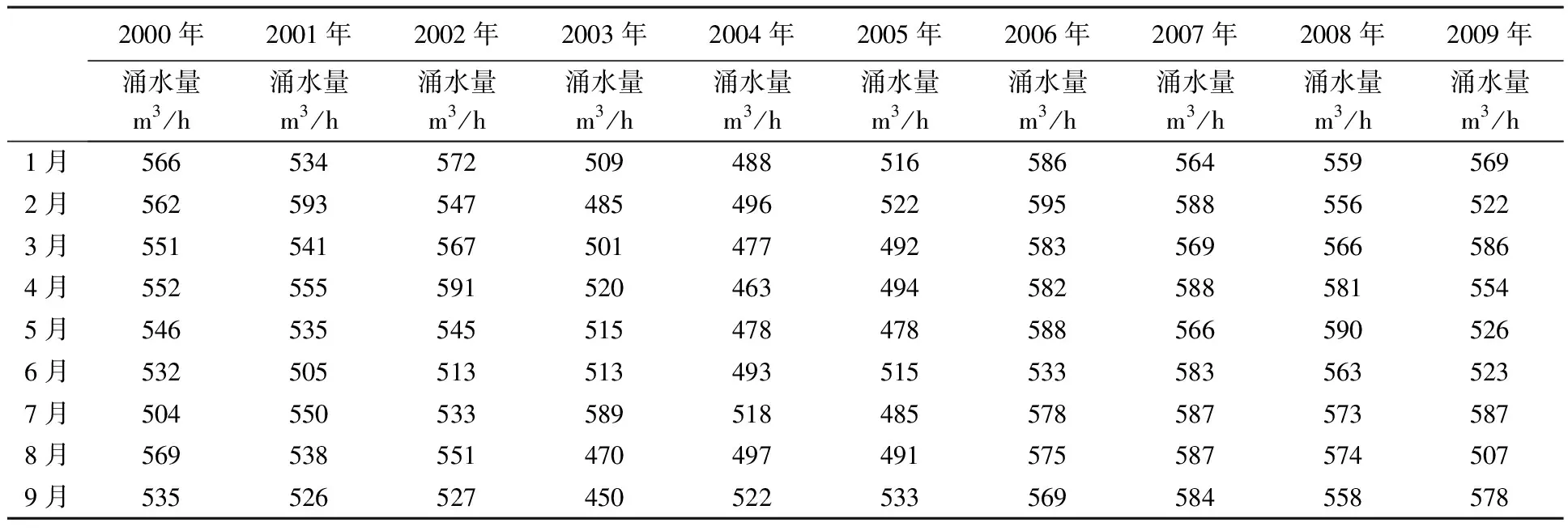
表1 某矿近20年月度涌水量数据统计表

续表
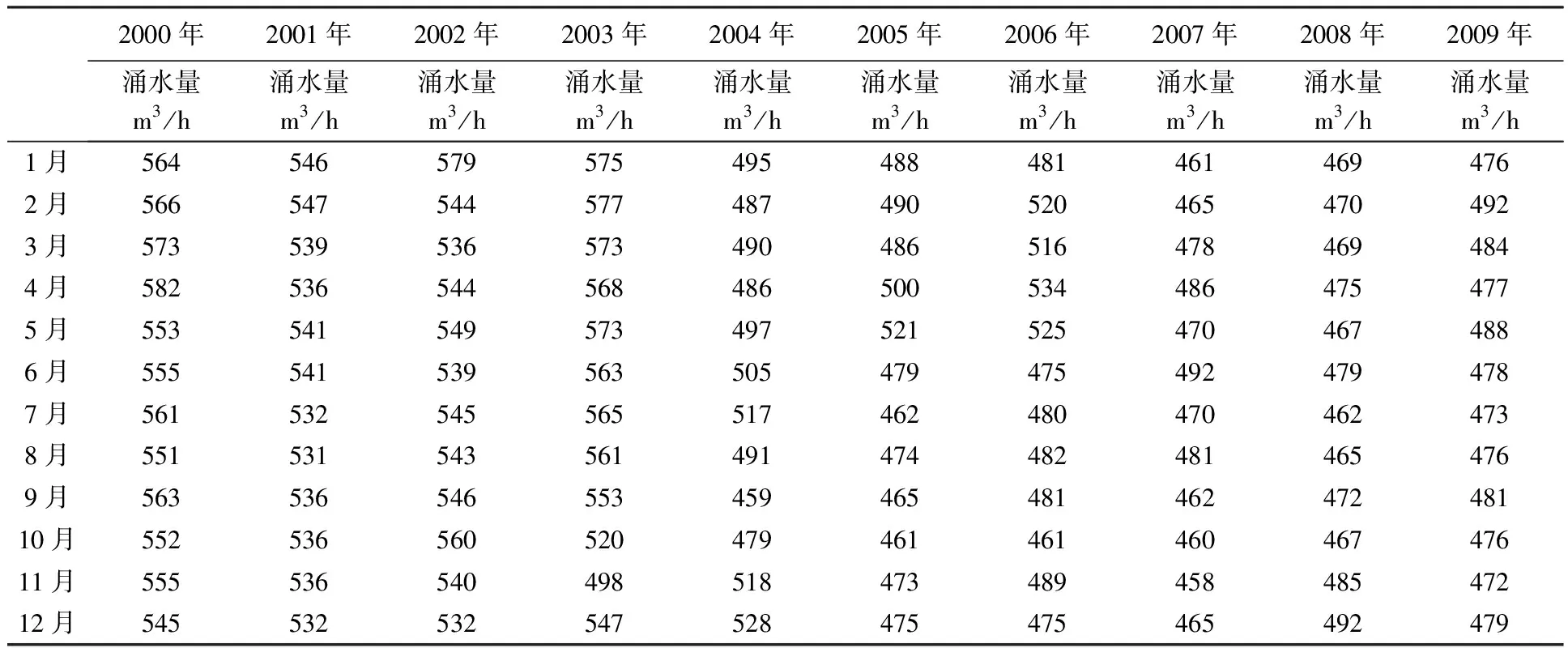
表2 某矿近20年月度涌水量数据统计表
2.1 传统ARIMA模型建模
利用SPSS软件做出涌水量时间序列图如图1所示。

图1 涌水量时间序列图
由图1可以看出涌水量的月度平均值波动较大,为非平稳序列。需要对其进行一阶差分处理使其平稳化;波动幅度随时间变化并无逐渐增大或减小的趋势,因此选用加法模型。
经一阶差分过的数据如图2所示。
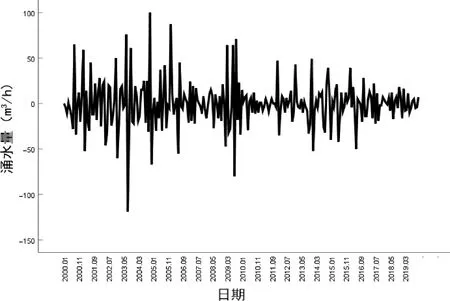
图2 一阶差分后的涌水量时间序列图
可以看出,在经过一阶差分以后,涌水量数据基本呈平稳化发展趋势。检测数据平稳化一般常用的方法是单位根检验[13],即ADF检验。利用Eviews软件完成一阶差分序列的单位根检验。单位根检验结果如表2所示。
得到的显著性检验值t值为-18.13316,小于1%、5%、10%水平的临界值,且得到的概率值p=0。证明一阶差分序列为平稳序列。

表3 ADF检验水平对应表
经过平稳性检验后,通过对p值和q值的多次设定,最终确定ARIMA(1,1,1)模型拟合效果较好,残差检验结果如图3所示。结果表明,残差序列通过了白噪声检验,模型已经得到了较好的拟合[14]。
根据拟合结果,确定自回归系数φ为0.68;移动平均系数θ为0.673,常数为48.633。由此建立不考虑相关因素的传统ARIMA模型:
yt=0.68yt-1+0.673ζt-1+48.633
(3)
预测结果与实测数据拟合曲线如图4所示,其中日期为从2000年1月开始计数的月数。
由拟合图可以看出,在前半段数据波动较为强烈时,拟合结果较好,当后半段数据变化转为平缓时,拟合曲线与实测曲线有较大差距,且在一段时间内的数据波峰及谷底表现尤为明显。
2.2 季节分解加法模型建模
矿区资料显示,大气降水为矿区主要充水水源,且考虑到涌水量大小是多种因素共同影响的结果,因此有必要考虑其他因素,建立季节分解加法模型,以提高预测精度。
2.2.1 趋势—循环因子(T-C)提取
考虑到涌水量的长期变化趋势恰恰是一种以年份为单位的循环,且在所选取数据年限跨度长的情况下,忽略短期波动,直接将趋势因子和循环因子合并为一项提取,进行长期预测。
季节变动和随机变动通过移动平均法予以消除[15]。考虑到本文是以月度涌水量数据进行统计,以季节为移动区间,因此选用跨度N=3进行相加平均。得到的数据既通过移动消除了季节的影响,又通过平均消除了随机误差的影响。而为了提升预测精度,需要对得到的数据再进行多次循环移动平均。经过多次实验后,发现进行7次移动平均后的数据和原始数据拟合效果较好。
观察到原始数据有较多峰值波动,因此选用傅里叶公式进行拟合;利用Matlab软件完成对拟合曲线的参数计算。
趋势—循环预测方程为:
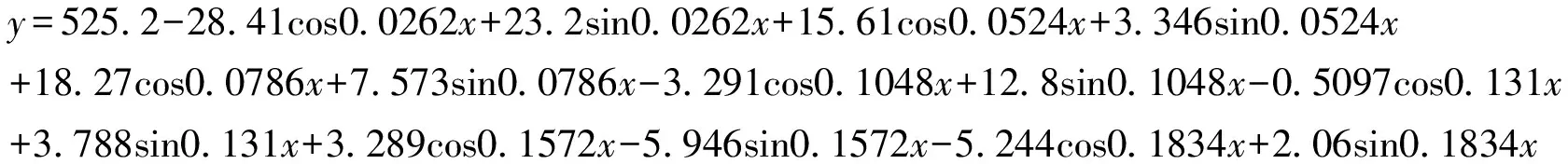
(4)
式中,x为从2000年1月开始算起的月数。
第7次移动平均线及拟合曲线对比图如图5所示。
2.2.2 季节指数(S)提取
利用SPSS软件,以12为周期长度进行季节性分解。所得季节因子为:1.976、3.880、2.307、7.288、1.731、-6.324、3.816、-4.254、-4.954、-6.853、1.334、0.053。从2000年1月开始,以一个月为单位,以12为周期长度进行循环,获得研究时段内每月所对应的季节指数。
2.2.3 随机变动(I)的提取
提取完趋势因子、循环因子以及季节因子后,通过式2得到随机变动因子。
随机变动的趋势图如图6所示。

图3 残差检验结果
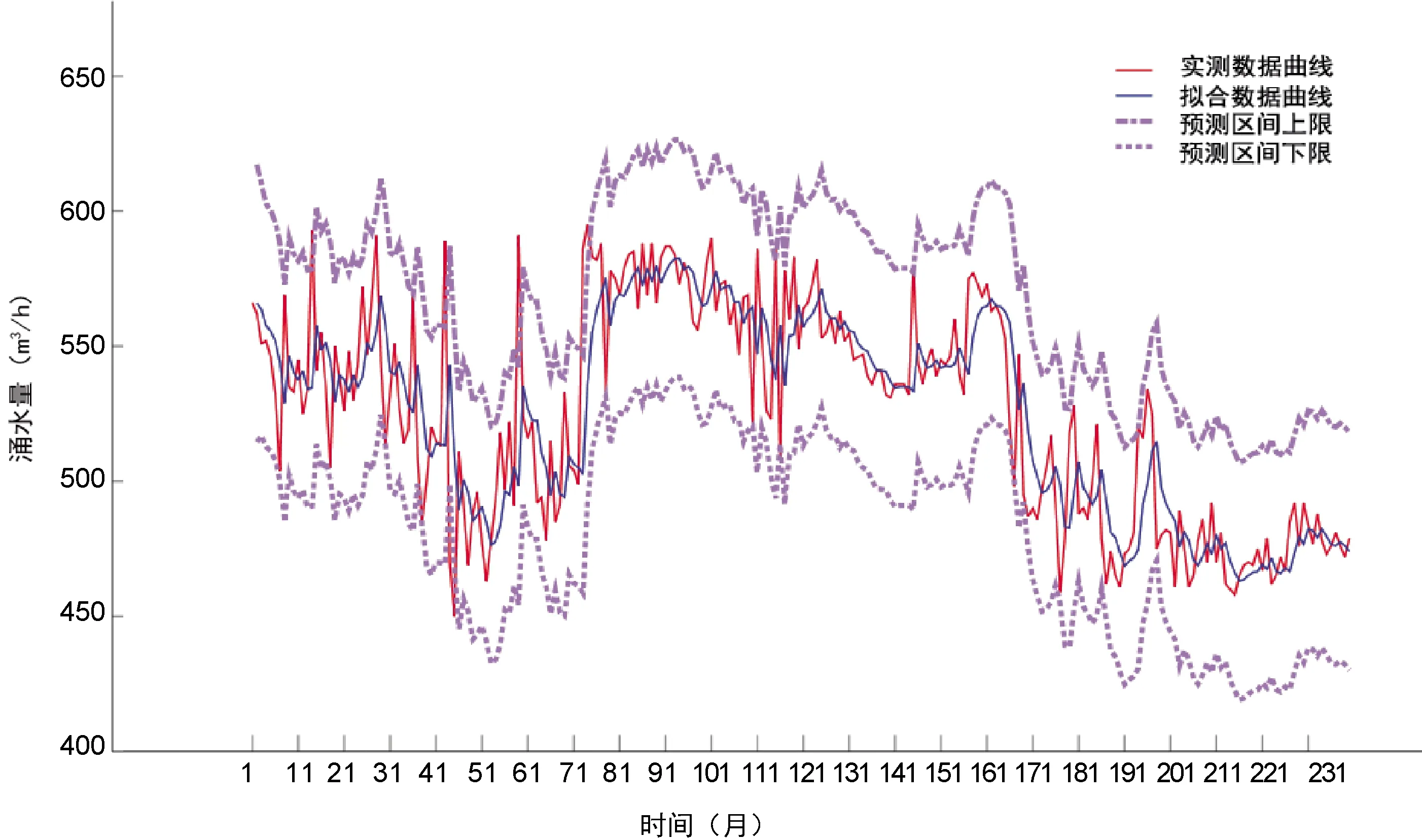
图4 实测数据与预测数据对比图
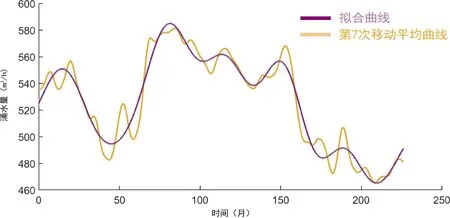
图5 第七次移动平均线及拟合曲线对比图
可以看出,月度涌水量的变化集中在[-50,50]区间内,利用Excel软件的随机函数功能来实现随机波动的模拟预测。
具体代码为“=RAND*100-50”
2.2.4 重新建立回归模型
将上述提取出的趋势-循环因子、季节指数和随机变动归类整理相加,重新建立起工作面涌水量的预测模型,其数学模型表现形式为:
(5)
式中,Yt为涌水量预测值,x为从2000年1月开始算起的月数,St为所对应的季节指数,It为通过函数所随机生产的波动值。
3 对比分析
分别用传统的ARIMA模型和季节分解加法模型对2020年上半年6组数据进行预测,结果见表4。
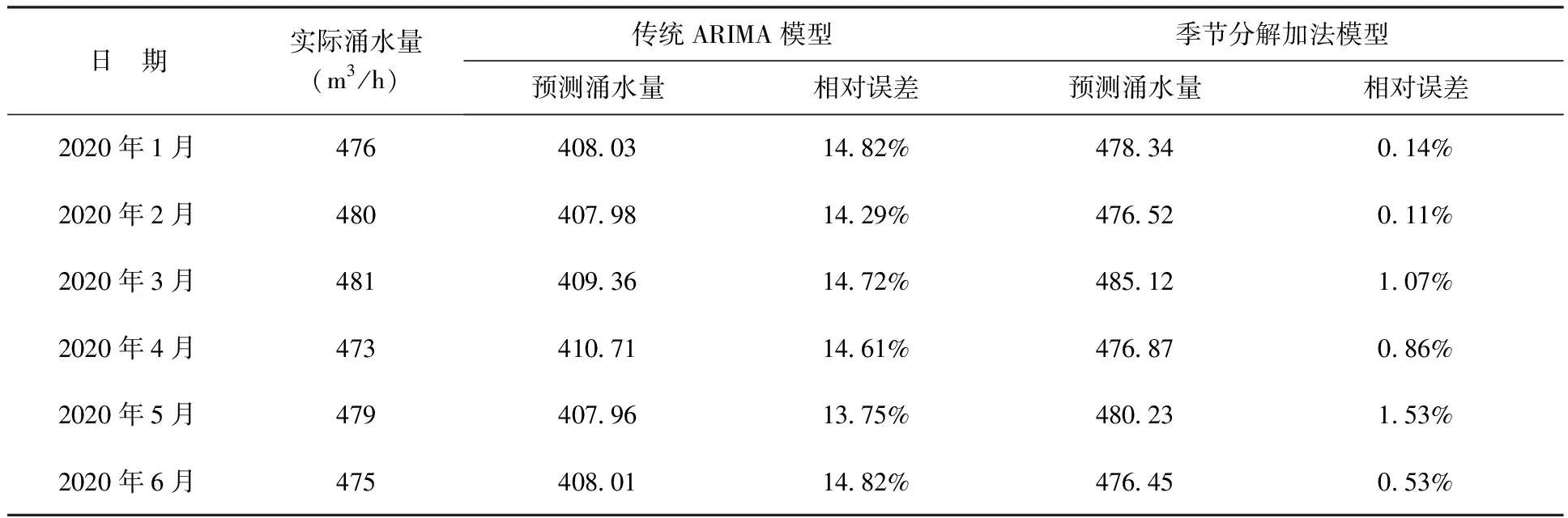
表4 传统模型与季节分解加法模型预测结果对比图
结果表明,利用传统的ARIMA模型对矿区2020年上半年涌水量进行预测,预测结果的相对误差基本在13%~15%范围内,误差较大,而通过对ARIMA模型实现季节分解后再预测,预测结果的相对误差控制在0~2%范围内,预测精度有了大幅度提高。
4 结论
(1) 利用传统的ARIMA模型对某矿明显具有季节特征的涌水量进行预测,预测误差较大,在对模型进行分解提取出趋势—循环因子、季节指数和随机变动后,重新建立起预测模型,预测精度有了大幅度提升,基本实现无偏差预测,为煤矿防治水工作中的涌水量预测难题提供了新的方案和思路。
(2) 在对涌水量信息进行多因素分解后预测结果的精度提升表明:在诸如突水危险性评价、危险系数确定等煤矿定量化作业过程中应当综合考虑多因素多变量的影响。
(3) 在数据的平稳化处理过程中,需要考虑到极端数据的影响情况,因此,在模型的后续完善工作中,可以考虑将滤波算法加入到模型中来,排除不良数据的干扰。
