基于复值稀疏贝叶斯的Hilbert变换计算方法
2021-07-27谢伟翔
谢伟翔,莫 艳
(广东工业大学 应用数学学院,广东 广州 510520)
Hilbert变换是信号分析与处理中的重要理论工具。由于复值Cauchy核在原点的奇异性,所以关于实部的Hilbert变换的计算是一项艰巨的任务[1-2]。计算Hilbert变换最常用的方法是快速傅里叶变换(Fast Fourier Transform, FFT)。最近,在文献[1-2]中给出了一些计算Hilbert变换的新方法。对于L2空间中的连续函数及C3∩L2的函数,学者们分别提出了两种样条的方法去计算Hilbert变换,从逼近精度上两种样条方法均优于FFT。随后,在文献[3]中首次使用复解析方法,提出了利用自适应傅里叶分解(Adaptive Fourier Decomposition, AFD)方法来计算Hilbert变换,充分利用解析空间中信号的实部和虚部是由Hilbert变换相关联的实值函数的特点来计算Hilbert变换。此方法适用于一般的非光滑和非连续信号,并提供显式的有理函数逼近,Takenaka-Malmquist (TM)系在有理函数逼近中起了重要的作用。虽然利用AFD计算Hilbert变换取得了较好效果,但其基于最大选择原理来自适应地选择最佳参数时,需要穷尽单位开圆盘中所有点,非常耗时。
近年来,稀疏贝叶斯学习方法成为机器学习中的一个研究热点,它是贝叶斯优化中十分重要的一类,是在贝叶斯理论的基础上发展而来,改进后的贝叶斯理论在文献[4]中也有提到。建立在稀疏贝叶斯学习基础上的学习机器称为相关向量机(Relevance Vector Machine, RVM),由Tipping[5]在2000年提出。它能够利用数据自身的特性对信号和图像实现最优的稀疏表示,已应用到智能检索、数据挖掘等领域。大多数基于稀疏贝叶斯的算法处理的是实值数据,然而在实际应用中还有许多复值信号需要处理。在文献[6]中利用同一信号实部与虚部具有相同的稀疏形式提出了复值贝叶斯压缩感知算法。本文将提出基于Szegö核的复值稀疏贝叶斯学习算法(Complex Relevance Vector Machine, CRVM),构造基于Szegö核的稀疏贝叶斯学习的Hilbert变换计算方法。基于Szegö核的稀疏贝叶斯学习算法,可以得到稀疏的有理逼近。事实上,由于TM系可通过对Szegö核做Gram-Schmidt正交化过程得到,因而基于Szegö核的稀疏贝叶斯学习算法也可以看成自适应傅里叶分解的一种,相比于AFD, 它的优势在于不需要穷尽单位开圆盘所有点去选择参数,并且最终所得到的模型是稀疏的。
对于给定能量有限信号s,由著名的Plemelj公式[7]有

如果s(t)是给定的实信号,那么有
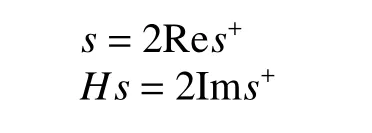
解析信号形成L2(R)的一个封闭的子空间,即Hardy空间H2(R)。相应的上半平面的解析函数构成了Hardy空间H2(C+)。 Hardy空间H2(R)和H2(C+)是等距同构的。
对于周期信号,也有类似的理论。对于一个有限能量的周期信号s,有

有限能量的周期解析信号构成了L2(∂D)的一个闭子空间,称其为单位圆周的Hardy空间,记为H2(∂D), 单位圆周的Hardy空间H2(∂D)与单位圆盘的Hardy空间是H2(D)同构的。本文将讨论单位圆周的情况。
1 基于Szegö核的CRVM
有理正交系,也称为TM系,在自适应傅里叶分解中起了十分重要的作用,在单位开圆盘空间D中,TM系定义为

CRVM将基于贝叶斯公式进行推导,它研究的是将一个函数运用贝叶斯模型概率表示为多个基本函数的线性叠加。稀疏贝叶斯学习与支持向量机都具有共同的核函数形式,然而稀疏贝叶斯学习可通过迭代优化删除大量的训练样本和核函数且不需要进行参数控制,仅根据训练样本自动调整,它能够充分挖掘和利用数据的先验信息,不仅可以减少异常值的影响,而且可以“剔除”大量不必要的基。


训练目标值的似然分布通过对权值变量进行积分,即

2 收敛性
基于Szegö核的稀疏贝叶斯学习采用最大期望算法(EM算法)或第二类最大似然估计进行参数的迭代,由算法的性质可以保证每次迭代都降低成本函数,直到达到一个稳定点。因而基于Szegö核的稀疏贝叶斯算法是全局收敛的。
3 实验
下面将以一个例子来说明该方法的有效性。本文研究了文献[3]中的单位圆盘内的奇异函数:
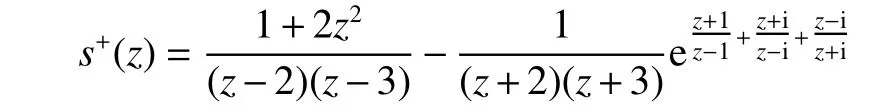
显然s+是一个解析信号或说是在H2(D)内解析的信号。由于解析信号的虚部是其实部的Hilbert变换,当有理解析函数序列逼近一个解析信号时,该序列中函数的实部和虚部分别逼近原始的实值信号及实值信号的Hilbert变换。图1、图2和图3分别给出了利用CRVM、FFT及AFD求Hilbert 变换的结果。

图1 s +(z)的虚部与CRVM得到的Hilbert变换比较Fig.1 Comparison of the imaginary part of s +(z) and the Hilbert transform given by CRVM
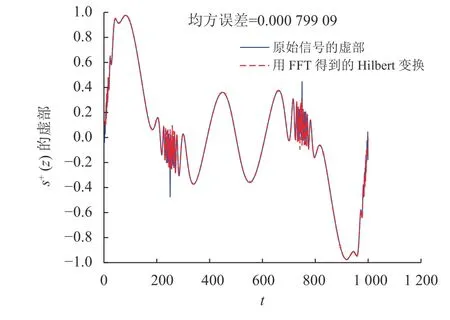
图2 s +(z)的虚部与FFT得到的Hilbert变换比较Fig.2 Comparison of the imaginary part of s +(z) and the Hilbert transform given by FFT

图3 s +(z)的虚部与用AFD得到的Hilbert变换比较Fig.3 Comparison of the imaginary part of s +(z) and the Hilbert Transform given by AFD
近似结果显示,所提方法CRVM效果优于AFD和FFT。在解析信号s+(z)虚部的高振荡部分,CRVM和AFD逼近效果优于FFT, 而且CRVM和AFD能给出逼近函数的解析表达式,便于后续应用,而FFT只能得到一组近似的离散数据。比较AFD和CRVM,显然CRVM所用基的个数少于AFD,而且其逼近效果优于AFD。另外,CRVM由于不需要每一步在单位圆盘内根据最大选择原理选择参数,所用计算时间及复杂度远远小于AFD。
4 总结
本文提出了基于复值稀疏贝叶斯定理近似计算Hilbert变换的方法。该方法是一种复解析方法,适用于所有能量有限的信号,能够在计算Hilbert变换的同时给出解析信号的稀疏有理逼近。与AFD方法相比,所提方法不需要穷尽单位圆盘的点去寻找参数,运算速度快且具有稀疏性。实验结果验证了所提方法的有效性。
