基于粒子群算法的码垛机器人时间轨迹优化研究
2021-07-27徐尤南刘志强
徐尤南,刘志强,陈 洁
(华东交通大学机电与车辆工程学院,江西 南昌 330013)
随着自动化生产的日益普遍,机器人的应用越来越广泛, 码垛机器人一直以来也是厂家争夺的重要市场之一, 码垛机器人在流水作业生产线中的应用十分广泛, 是表征工业自动化水平的重要标志[1-3]。 而在机器人的研究中,轨迹规划是一个重要模块,它对提高机器人的工作效率至关重要[4]。 机器人轨迹规划中路径的设定可在关节空间坐标,也可在笛卡尔空间坐标[5]。 笛卡尔空间轨迹规划通俗易懂,但矩阵运量大,其坐标值不易测量,难以实时控制。 关节空间轨迹规划可根据设计实时调整轨迹角度在时间上的变化,可避免运动过程中机构奇异或冗余现象,可控性好,故使用较为广泛[6]。
最优轨迹规划是工业机器人最优控制问题之一,规划的任务是根据给定的路径点规划出通过这些点并满足边界约束条件的光滑的最优运动轨迹[7]。轨迹优化有时间最优和能量最优两种,前者使用较为广泛。
时间最优最早由Lin[8]中提出,其目的是最大化操作速度而最小化操作时间[9]。 机械臂关节空间轨迹规划大多采用样条插值的方法[10]。 三次样条插值的最优时间轨迹优化使用广泛, 计算也相对简单。但对轨迹跟踪精度更高,受振动影响更大等要求较高的机械手,最小脉动和脉动连续轨迹规划受到密切关注。 朱世强等[11-12]对5 次多项式及7 次B 样条插值方法做了研究,但计算量都较大。 提高插值平滑度和减小计算量成了一个矛盾问题。 采用分段插值由于计算量小,插值平滑等特点被广泛使用。 考虑脉动连续性,Xu 等[13]采用3-5-3 多项式对机器人轨迹进行规划,何平等[14]进行了修正。 何建成等[15]通过粒子群算法实现了工业机器人时间最优、能耗最小、脉动做优等多目标下的最优轨迹规划。刘帅等[16]基于粒子群算法对工业机器人智能打磨轨迹问题进行研究。 除此之外,粒子群算法在其他领域也得到广泛使用,如黄江平等[17]通过改进粒子群算法实现轨道列车节能控制优化,杨刚等[18]的手写数字识别研究等。
粒子群算法(PSO),其思想起源于鸟类捕食行为,模仿鸟类捕食的行为,关注个体行为与集体行为,是一种集体寻优的优化算法。 本文应用POS 优化算法,考虑运动约束并满足最大速度约束条件下对码垛机器人的一个码垛周期进行3-5-3 多项式轨迹最优时间求解。
1 系统
1.1 模型
本文以IRB460 码垛机器人为参考, 应用Matlab 工具箱Matlab Robotics 工具对码垛机器人进行建模, 通过机器人空间位姿及D-H 矩阵法, 通过Link 及SerialLink 构建关节并连接起来, 构成机器人结构模型,如图1 所示。
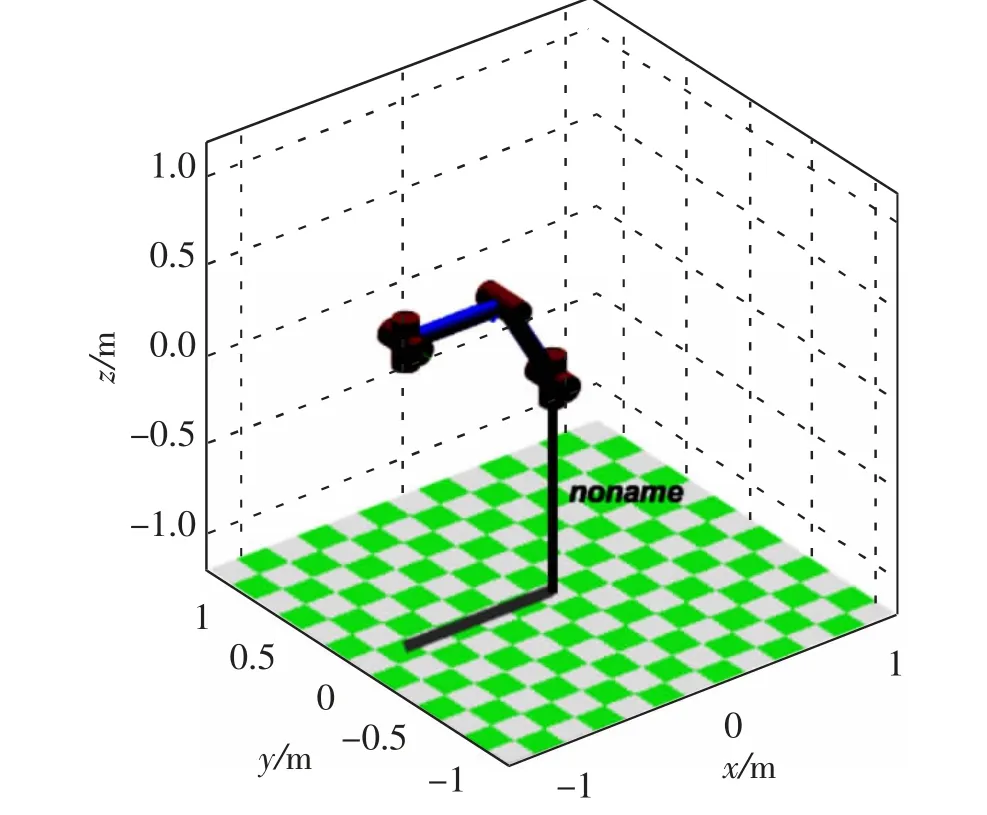
图1 IRB460 码垛机器人结构示意图Fig.1 Schematic diagram of IRB460 palletizing robot
1.2 路径描述
机器人运动规划一般被划分为两个子问题,即路径规划和轨迹规划。 前者描述的是机器人位置的空间移动轨迹,后者描述的是沿着这条路径的机器人位姿的时间历程。
运动路径的定义是轨迹规划的前提[19],码垛机器人的一个码垛周期包含4 个主要位置点,分别是起始抓取位置(起始点),抬起位置上方(路径点),放置位置上方(路径点),放置位置(结束点),本文针对该运动周期的路径进行轨迹研究。
2 码垛机器人运动学正逆解
在进行机器人运动正逆解之前,应建立其DH 参数表,如表1 所示。 表中ai为连杆长度;αi为杆之的转动力角度;d 为杆间长度;θ 为杆间角度;ai-1和αi-1描述连杆i-1 本身特征与下一连杆i 的变化联系。
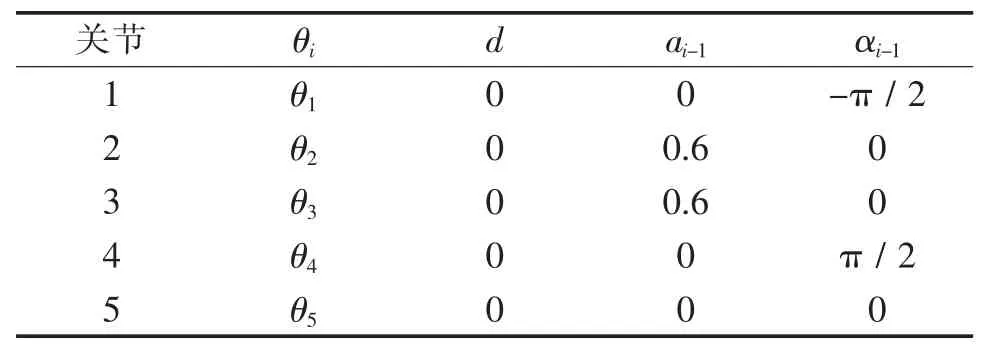
表1 D-H 参数表Tab.1 D-H parameters
同时还需建立机器人各关节坐标变换图,如图2 所示,在此基础上推导正反解析式。

图2 机器人各关节坐标变换图Fig.2 Coordinate transformation diagram of each joint of robot
关节1 坐标系的建立与初始坐标系完全相同,将关节1 坐标系和关节2 坐标系设于同一点;关节4,关节5 坐标系为腕关节坐标,位于同一点。5 个关节均为转动关节,转动变量分别为θ1,θ2,θ3,θ4,θ5。其中,a2,a3分别表示关节2,关节3 的关节长度。
根据机械臂各关节坐标变换可以建立该机器人的运动学正解算方程。
1) 各个连杆的变换矩阵Tii-1表示为

式中:si表示sinθi;ci表示cosθi。 sij表示sin(θi+θj);cij表示cos(θi+θj)。
3) 机器人末端执行器位姿T50表示为
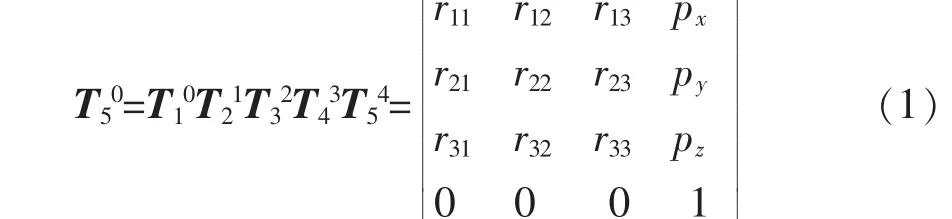
4) 计算各轴关节角度值
机器人末端执行器的位姿

已知机器人的期望位姿,可通过运动学逆解求解出各关节点的参数,同时得到关节在不同位置空间的角度插值。
3 轨迹规划
码垛机器人在代替人类完成搬运工作过程中,已知执行末端起点及终点的位置,容易通过运动学正逆解求出每个关节的位移, 以便对其进行轨迹规划,应用MATLAB 软件可对其在笛卡尔空间和关节空间参数进行分析。 利用jtraj 函数对码垛机器人4 点之间的3 段轨迹进行关节空间轨迹插值, 利用ctraj函数对码垛机器人4 点之间的3 段轨迹进行笛卡尔空间轨迹插值,其操作过程较为简单,具体从略。
4 轨迹优化
本文基于粒子群优化算法对码垛机器人一个码垛周期的轨迹进行时间优化。
4.1 优化目标
针对粒子群优化算法对码垛机器人进行轨迹优化这一问题,目标是满足机器人运动学约束条件下,所有关节运动的时间最短。 码垛机器人工作过程中主要是最大速度的约束,故优化问题的目标函数如式(18)所示,该式也是POS 优化过程中的适应度函数。 即满足最大速度约束的条件下,求一个码垛周期的最短工作时间。 约束条件如式(19)所示。

4.2 优化过程
码垛过程中机器人机械臂末端经过两个中间路径点,当已知起点,终点及两个中间路径点在直角坐标系下的位置,即给定机器人机械臂末端的期望位姿, 可得通过运动学逆解求出各个关节参数,并将笛卡尔坐标转化为关节空间坐标的各关节点在4 个插值点的关节角度,用θij表示,其中i 表示关节数,j 表示插值点序数。 表2 是机械手末端执行器在笛卡尔空间的路径插值点,表3 是通过运动学逆解求出各个关节点在4 个插值点的关节角度。
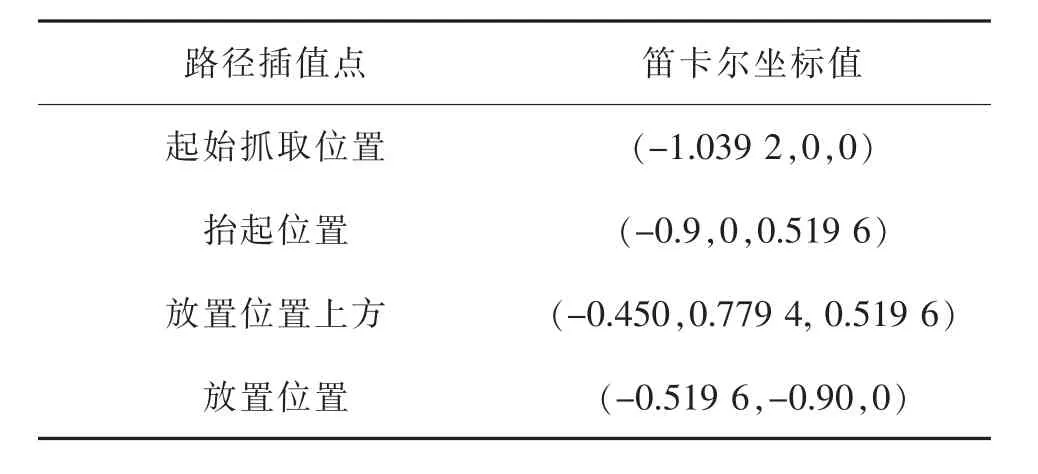
表2 笛卡尔空间的路径插值点Tab.2 Path interpolation points in Cartesian space

表3 关节空间的路径插值点Tab.3 Path interpolation points in joint space
当一个码垛周期的3 段轨迹采用3-5-3 样条多项式插值时,其轨迹表达式为

式中:li1(t),li2(t),li3(t)分别表示各关节3-5-3 样条多项式的运动轨迹;t1,t2,t3分别表示3-5-3 样条多项式插值的时间。
由此,可将多项式的系数作为寻优量。 又已知在始末点及中间路径点的速度和加速度均为0,且3 段运动轨迹是连续的。 得多项式系数与插值点关系为

由矩阵A 可知,寻优量的求解只与时间t 有关,所以选择时间变量t 作为搜索空间进行优化。 轨迹优化即满足运动学约束条件下,所有关节运动的时间最短。
应用粒子群优化算法进行码垛机器人码垛周期的时间最优求解时,将待求解的时间看作搜索空间的粒子,每个粒子都有自己的位置属性和速度属性,前者决定粒子的位置,后者决定粒子的飞行方向和距离。 所有粒子都会通过一个被优化的函数来判断适应度值并追寻最优。
在未找到最优解时,粒子都会通过循环迭代不断更新自己的速度和位置,即优化过程。 粒子优化包括个体粒子最优和群体粒子最优,个体最优粒子的更新方式从当前新粒子及个体最优粒子中选择支配粒子,两者无法支配时任选其一,群体最优粒子从已产生的最优粒子中随机选择一个。 来更新自己的位置和速度,更新公式如下
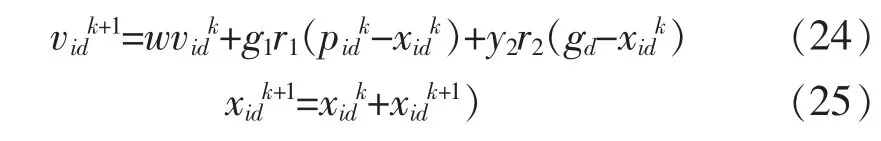
式中:ω 为惯性权重;k 为迭代次数;i 代表第i 个粒子;d 为设计参数的维度;y1,y2为学习因子(也可理解为粒子加速度常数);r1,r2为区间[0,1]之间的任意值; 粒子的位置xid∈[-xmax,xmax], 粒子的速度vid∈[-vmax,vmax],且都要符合该约束条件,若不符合将被边界值替代。 速度更新函数中,右边第1 部分是之前的速度乘以惯性权重,右边第2 部分是粒子自身的位置优化,反映粒子当前位置与粒子本身历史最优位置的差距,右边第3 部分粒子在全局的位置优化,反映粒子当前位置与群体历史最优位置的差距。 粒子位置更新则是上一次位置与当前速度叠加。
应用粒子群优化算法对某个关节进行时间最优规划流程如图3 所示,主要步骤为:

图3 粒子群轨迹优化流程图Fig.3 Flow chart of particle swarm optimization
Step1 初始化种群粒子,包括粒子位置和速度,个体最优位置,群体最优位置及种群规模;
Step2 求解矩阵A;
Step3 求解运动多项式, 判断是否满足速度约束;
Step4 评价粒子适应度;
Step5 当前适应度与个体历史最优适应度比较,求个体最优位置;
Step6 当前适应度与全局历史最优适应度比较,求群体最优位置;
Step7 更新种群的位置和速度;Step8 满足终止条件,或返回Step2;Step9 输出结果。
4.3 优化结果
在对机器人进行正逆解时发现,末端连杆的参数变化较大, 它也是码垛工作中最最终的执行元件,故本文以末端关节5 为例对机器人的一个码垛周期进行时间最优求解。 结果如表4 所示。
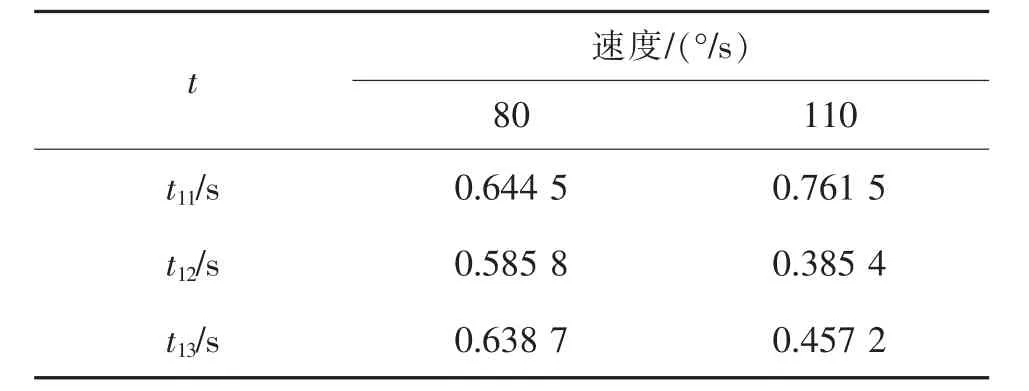
表4 关节5 最优插值时间Tab.4 Optimal interpolation time of Joint 5
如图4 所示分别是关节5 速度限制为80 °/s 及110 °/s 时最优粒子的位置变化图。 从图中可以看出,在迭代次数达到50 次以上,粒子是收敛的。 优化过程中将迭代次数设置为100 次,作为优化结束的结束条件。
从图4 可以看出,在迭代次数达到50 次以上,粒子迅速收敛。 且收敛值在给定的速度约束下。 优化过程中将迭代次数设置为100 次,作为优化结束的结束条件。关节5 的两种速度限制下经粒子群优化的3-5-3 多次多项式所需的3 段插值时间t,如图5 所示。
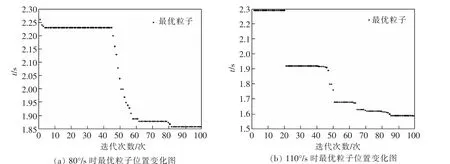
图4 最优粒子位置变化Fig.4 Optimal particle position change
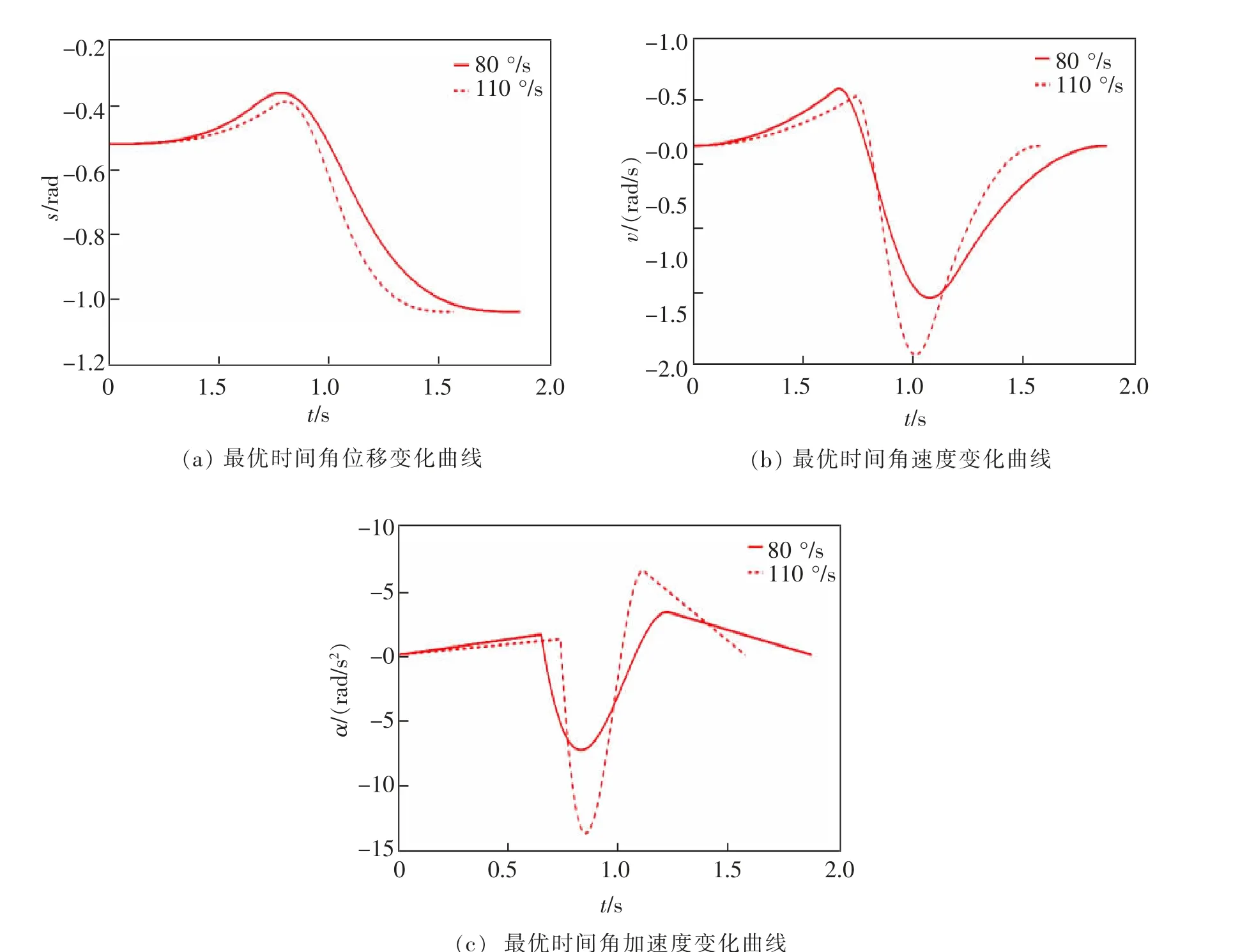
图5 最优时间关节5 运动响应曲线Fig.5 Motion response curve of optimal time Joint 5
从图5 可以看出,关节5 的角位移s、角速度v、角加速度α 均满足14 个运动学约束条件, 结果证明了采用速度约束下的POS 在计算机上离线寻找机器人3 段插值最优时间轨迹规划的可靠性。
5 结论
经研究得到以下结论:
1) 采用自适应惯性权重的约束粒子群算法寻找最优解,从而构造出机器人关节参数化曲线;
2) 该方法可以最大限度地提高末端执行器的可操作性;
3) 粒子群算法简单,参数易调整,弥补了多项式计算阶次高而使优化运算复杂的不足;
4) 粒子群算法中粒子在收敛末期容易形成振荡,模型不同时需要重新调整参数以达到最优结果。
