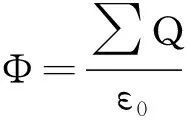电场的降维映射及电场线的绘制方法
2021-07-26岳国联黄绍书
岳国联 黄绍书
(六盘水市第三中学 贵州 六盘水 553000)
电磁学中,常用电场线形象直观地描述静电场(本文“电场”均指静电场),由高斯定理出发,可得到电场线的基本特征[1,2].为了较为“精确”地描绘共线分布点电荷产生的电场线,常规做法是先推导出电场线方程[3~10],再用计算机根据方程绘制[7~10];对于分布于平面内非共线电荷,可以借助软件对电场线微分方程进行数值求解并绘制[11].采用这些方法绘制电场线,总存在这样或那样的问题[2,3],本文将提出一种解决这些矛盾的有效办法.
1 电场线的特征
为了使电场线对电场强度的描述更加准确,结合高斯定理,对电场线做如下规定:电场线上每点的切线方向与该点的电场强度方向相同,穿过电场中任意一面元的电场线条数正比于该面的电通量[1].
由这个规定可以得出电场线的基本特征——电场线发自(止于)点电荷所在处;点电荷Q发出(终止)的电场线数与电荷量Q成正比;通过某一截面电场线数与该截面的电通量Φ成正比,无电荷处,电场线不中断[1,2].
由电场线的基本特征,可以得到电场线分布的另两个局部特征.
近距特征:由有限个点电荷形成的电场中,电场线均匀穿过以某电荷为球心、半径足够小的球面.原因是在这个点电荷周围足够近的地方,该点电荷产生的电场远大于其他电荷在该处产生的电场.
远距特征:点电荷分布在有限区域内,若总电荷不为零,电场线均匀穿过以电荷分布区域内某点为球心、半径足够大的球面.原因是在足够远处来看,这些电荷相当于集中于一点,电场强度相当于一个带有总电荷量的孤立点电荷产生的电场.
2 采用常规方法绘制电场线存在的问题
下面讨论采用常规方法绘制电场线存在的问题.为了便于求出电场线方程的解析解,取电荷分布在一条直线上.设所有电荷分布在y轴上,设第i个点电荷电荷量为Qi,位置坐标为(xi,yi),求经过xOy平面上任意一点(x,y)电场线方程,其方法有多种[3~11],其中利用电通量的方法和利用矢量线方程的方法最为常见[3~9],均得到如下电场线方程
(1)
其中C为常量,不同的C值对应不同的电场线.
取C的等差数值代入式(1),得到的电场线明显不能完全满足电场线的基本特征,故需要进一步改进,很多文献提到一些办法,例如取一些特殊C值代入式(1)来绘制,特殊值的选取依据就是使其满足近距特征或远距特征[7,9,10].
设单位电荷q产生的电场线数为n0=16,电荷量Q1的位置坐标(0,1), 电荷量Q2的位置坐标(0,-1),笔者在Mathematica中依照近距特征或远距特征确定值,绘制电场线图像如图1、图2所示.
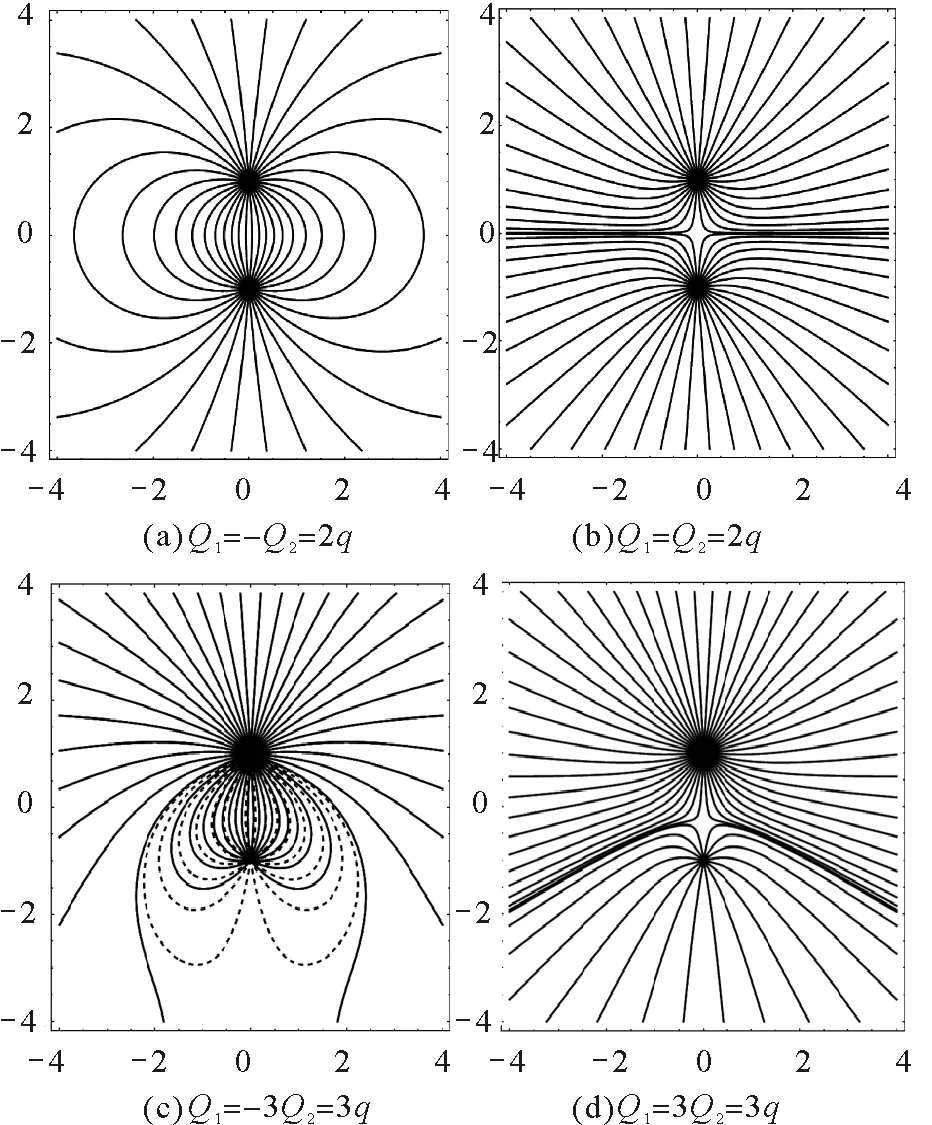
图1 按照近距特征确定C值绘制电场线

图2 按照远距特征确定C值绘制电场线
图1按照是按照近距特征确定C来绘制,一定都满足近距特征.
图1(a)中是等量异种电荷的电场线.Q1发出满足近距特征的电场线,与终止于Q2满足近距特征的电场线完全重合,两个电场线周围均满足近距特征,电场线没有延长到远距离空间去,不能存在远距特征;图1(b)和(d)中是同种电荷电场线.两个电荷周围电场线均满足近距特征,但不满足远距特征,电场线之间似乎有一种挤压的现象,说明近距特征与远距特征间存在矛盾;图1(c)中,是非等量异种电荷电场线.实线是Q1发出满足近距特征的电场线,虚线是终止于Q2满足近距特征的电场线,实线与虚线无法完全重合,说明近距特征间存在相互矛盾.
图2是按照远距特征确定C来绘制,一定满足远距特征.
图2(a)中是孤立点电荷的电场线.同时满足远距特征和近距特征;图2(b)和(d)中是同种电荷电场线.满足远距特征,但不满足近距特征,说明近距特征与远距特征间存在矛盾;图2(c)中是异种电荷的电场线.满足远距特征,但是由于部分电场线从正电荷到负电荷,并没有延伸到较远空间去,无法在远距特征中加以体现,所以无法绘制.
从以上分析可以看出,除孤立点电荷、等量异种电荷的电场线外,其他分布点电荷的电场线均不能满足电场线的基本特征.各电荷间近距特征相互矛盾、近距特征与远距特征间相互矛盾的现象,一些文献也指出了这个问题[2,3],也有因此将电场线的特征作为“绘制电场线图的附加规定”[2].
笔者认为,绘制满足电场线的基本特征,就是绘制电场线图的规定,没有必要加上“附加”.因为由高斯定理得到电场线的基本特征体现了电场的某个基本属性,三维空间中描述电场的电场线是空间曲线,他们一定满足其电场线的基本特征(包括近距特征和远距特征),而某个平面内的电场线只是众多电场线的一部分,该部分电场线无法满足电场线的基本特征也正常,就像将地图绘制到平面上时,总会导致变形是一个道理.这并不是绘制中改进方法完不完善的问题,也不是技术高超不高超的问题,而是原本就该如此.
3 电场和电势的降维映射
通过前面分析可知,对于分布在平面内的一般电荷,通过电场线方程中C取特殊值的改进方式绘制该平面内的电场线,是不可能完全满足电场线的基本特征的.要能在平面内绘制出完全满足其基本特征的电场线,需要从电场本身着手,进行一种变换,使三维空间的电场降维映射到二维空间中去.
3.1 电场的降维映射及电场线绘制
为使平面内电场线完全满足电场应具有的特征,将电场从三维空间降维映射到二维空间去,映射后的电场是一种假想的电场,姑且称为映射电场,记为E,其电场线称为映射电场线,封闭曲面S对应为封闭曲线C,电通量对应于映射电通量Φ.
类比高斯定理,假设映射电场在二维空间内遵从“二维高斯定理”,即
(2)
由式(2)得到,二维真空中位于(x0,y0)点电荷Q在距点电荷r的(x,y)处产生映射电场为
(3)
式中ε0是真空介电常量;er是从Q位置坐标指向(x,y)的单位矢量.映射电场仍为矢量,方向与电场方向规定一致.
在二维空间多个点电荷形成的映射电场中,其映射电场穿过某曲线的映射电通量的等高线为映射电场线.如图3所示,穿过曲线C的映射电通量为Φ,若将曲线C的A端固定,则映射电通量Φ为B点坐标(x,y)的函数,对应的就是映射电场线方程.
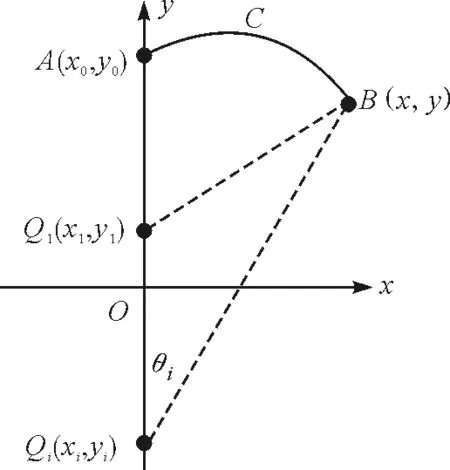
图3 二维映射电场的映射通量等高线求解示意图
设第i个点电荷位于(xi,yi),取y轴正方向映射电通量为零(图中A点),则位于(x,y)处的B点对应映射电通量
(4)
其中θi为研究曲线两端与第i个电荷连线的夹角.用直角坐标表示有
(5)
设单位电荷q产生的电场线数为n0.每个常量Φ值对应一条映射电场线,等间距取Φ值,第j条电场线对应
(6)
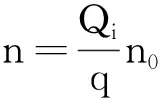
下面以等量同种电荷为例,设单位电荷q产生的电场线数为n0=16,在Mathematica中编写代码如下:
n0=16;(*单位电荷数*)
Q={2,-2};(*电荷列表,对应Q1,Q2,Q3*)
X={0,0};(*电荷x轴坐标列表*)
Y={1,-1};(*电荷y轴坐标列表*)
φj=Table[(2j+1)2Pi/(2 n0),{j,-Length[X] n0,Length[X] n0-1}];(*计算φj,考虑到定义域问题,需要扩大φj 值范围*)
p1=ContourPlot[Sum[Part[Q,j]ArcTan[(y-Part[Y,j]),(x-Part[X,j])],{j,1,Length[X]}]= =φj,{x,-4,4},{y,-4,4}, AxesOrigin->{0,0},ContourStyle->{Black},PlotPoints->50,AspectRatio->1,Frame->True,FrameStyle->Black];(*绘制映射电场线*)
p2=ContourPlot[Sum[Part[Q,j]ArcTan[(x-Part[X,j]),(y-Part[Y,j])],{j,1,Length[X]}]= =φj,{x,-4,4},{y,-4,4}, AxesOrigin->{0,0},ContourStyle->{Black},PlotPoints->50,AspectRatio->1,Frame->True,FrameStyle->Black]
Show[p1,p2] (*重叠两张图片,显示更加完整*).
得到电场线如图4(a)示,同理适当修改代码,可得到其他图像,如图4中其他图所示.

图4 共线电荷与映射电场线
由图可以看出这映射电场线完全满足电场线的基本特征(包括近距特征与远距特征),在绘制时不需要单独设定.
对于等量异种点电荷,对比图4(a)与图1(a),它们虽然都满足电场线的基本特征,但是电场线形状有一定区别.图1(a)之所以满足电场线的基本特征是因为它没有远距特征,而且两个电荷量相同的特殊情形的结果,具有特殊性,而图4(a)中满足电场线基本特征是一种普遍性结果,是“二维高斯定理”的体现,有本质的区别.
值得一提的是,式(1)仅适用于共线点电荷的电场线方程,而式(5)不仅适用于共线点电荷的映射电场线方程,还适用平面内非共线多个点电荷的映射电场线方程,在Mathematica中绘制部分实例如图5所示(代码略),设单位电荷q产生的电场线数为n0=16.

图5 平面内非共线点电荷与映射电场线
3.2 电势的降维映射及等势线的绘制
在三维空间绘制等势面是比较容易,效果也很理想,但是为了绘制与映射电场线相互正交的等势线,需要将电势也作映射,姑且称为映射电势,用φ表示其等势线称为映射等势线.
类比三维空间电势及电势差的定义,在第i个点电荷产生的映射电场中,A和B两点与点电荷距离分别为riA和riB,结合式(3)则A和B间映射电势差
(7)
用ri表示研究位置到参考面的距离,取B点映射电势为零(零势能参考面),位于任意点(x,y)的映射电势为φ,则
φ取等差数值代入式(8),就得到在xOy平面内等差的映射等势线.
在Mathematica中用以下代码绘制等势线:
p3=ContourPlot[-Sum[-Part[Q, i] Log
[Sqrt[(x + Part[X, i])^2+(y-Part[Y,i])^2]],{i,1,Length[X]}],{x,-4,4},{y,-4,4},AxesOrigin->{0,0},ContourStyle->{{Black,Dashed},{Black,Dashed}},PlotPoints->50,ContourShading->None,Contours->16,ContourLabels->Automatic,Frame->True,FrameStyle->Black];(*绘制映射等势线,虚线*)
Show[p1,p2,p3](*映射等势线加在映射电场线上*)
在图5(c)加上映射等势线后如图6所示.
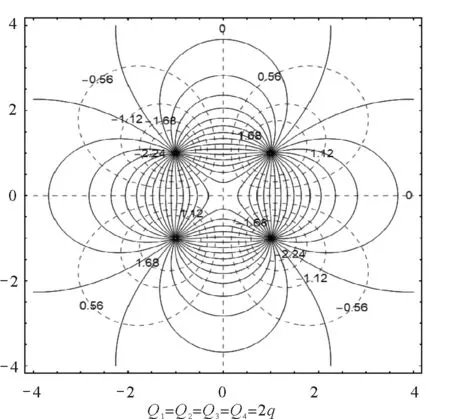
图6 映射电场线及映射等势线(虚线)
三维空间与二维空间中电场相关物理量关系如图7所示.

图7 三维与二维空间中电场相关物理量对应关系
4 结束语