基于机器学习的纵向缺失值处理方法在体育科学研究中的应用
——以运动对大学生执行控制影响的纵向研究为例
2021-07-26孙志远陈爱国史一凡
孙志远,陈爱国,2,熊 轩,朱 昊,史一凡
(1.扬州大学体育学院,江苏扬州225127;2.扬州大学体育运动与脑科学研究所,江苏扬州225127)
近年来,随着体育科学研究的不断深入,纵向实验研究在体育科学研究中越来越多,但在研究过程中由于外界因素干扰或研究参与者自身原因等,后测数据容易缺失。如果不能可靠地处理缺失数据,将导致分析结果产生潜在的偏差,甚至会得出误导性的结论[1]。以往采用按照一定规律,选择合理的数据对缺失数据进行替换的插补方法来处理缺失值,得到“完全数据集”后,再使用数据统计方法对数据进行统计分析与统计推断[2]。常用的插补方法有回归替换法、均值替换法和多重替代法等。但插补方法的选择会受到缺失数据的比例、变量间的关联度和时间限制等因素的影响,并且在不同的数据缺失模式和分布模式下,选择不适合的插补方法仍然会使数据产生偏离,得出错误的结果[3]。如何科学可靠地处理后测数据的缺失值,成为一个摆在研究者面前需要解决的难题。
机器学习是一门多领域交叉学科,专门研究计算机如何模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能[4]。随着人工智能浪潮的到来,作为人工智能核心的机器学习被广泛应用于各个学科领域。临床医学使用机器学习算法建立疾病诊断、疗效判断预测模型[5];电气工程领域通过机器学习算法对短期电力负荷进行预测[6];经济学把机器学习应用于复杂经济和金融网络中[7]。机器学习在预测中的可靠性受到各大领域的强烈响应。相比之下,在将机器学习如何应用于处理体育科学研究中的后测数据缺失值方面尚无针对性研究;与常用的一些插补法处理缺失值相比,机器学习建立的预测模型适合任意缺失模式,对数据的分布类型要求较低,模型的拟合效果好,且稳健性好,偏差小[8]。因此,基于机器学习建立应用于体育科学研究中后测数据缺失值的预测模型是非常有必要的。
本研究以运动对大学生执行控制影响的纵向研究为例,全面地介绍如何应用机器学习来处理体育科学研究中的后测数据缺失值。执行控制是指在认知过程中有意识地对自动的、占主导地位的优势反应的抑制,包括阻止与情境不适宜的优势反应进入,终止被部分激活但与目标无关的信息进入,抑制不相关信息的激活[9-10]。执行控制作为个体认知、情绪和社会功能的核心,对其身心健康发展有着极其重要的作用[11-13]。寻找改善执行控制的有效途径已成为各个学科和社会共同关注的热点问题。近些年的研究发现,基线有氧适能和基线执行控制与后测执行控制有着密切的关系[14-17]。基于此,本研究选择通过基线有氧适能和基线执行控制对后测执行控制的缺失值进行预测。
综上所述,本研究选择机器学习算法建立预测模型,以基线有氧适能和基线执行控制为模型特征,对后测执行控制的缺失值进行预测,旨在探索纵向缺失值处理的新方法,为机器学习应用于体育研究中后测数据缺失值的处理提供实践基础。
1 方法
1.1 数据来源
研究对象为通过网络和发放调查问卷的方式在扬州某大学招募的89名(男/女:36/53)在校大学生。所有研究参与者填写了身体活动问卷和SCL-90症状自评量表,并进行了心肺功能检查,色觉和(矫正)视力正常,研究参与者的生理和心理状况正常,适合参加本研究。
随机将所有的研究参与者分为实验组和对照组,在实验期间,实验组进行10周有氧运动,对照组进行常规活动。最大摄氧量是能够反映人体有氧适能水平最直接的指标[15],研究选用功率自行车(Elmed EGT 1000)来测量最大摄氧量[16]。使用陈爱国[17]开发的执行控制评价和测量方法,通过Flanker任务对执行控制进行测试。评价指标为不一致条件下的平均反应时减去一致条件下的平均反应时,差值越小,执行控制越好。
1.2 机器学习算法的选择
研究选择机器学习中的支持向量计算法来建立预测模型。支持向量机采用结构风险最小化原则,在小样本条件下仍然可以获得良好的拟合能力[18]。支持向量机模型的最终预测结果由少数支持向量决定,对异常值不敏感,具有较好的“鲁棒性”[19],算法也相对简单。支持向量机还可以通过可靠的已知算法得到目标函数的全局最小值,将学习问题表示为凸显优化问题[20]。
2 支持向量机预测模型
2.1 支持向量机算法
支持向量机算法求解回归问题是在高维特征空间中进行的,高维特征空间中的数据是输入数据通过非线性变换后的映射[21]。
设给定训练集为{(x1,y1),(x2,y2),...,(xn,yn)},n表示训练集数据数量,xi为输入特征向量,yi为输出值。设定目标函数:

式中:w和b为支持向量机的参数。
引入松弛变量ζ≥0和ζ*≥0将目标函数进行转换:

约束条件为:
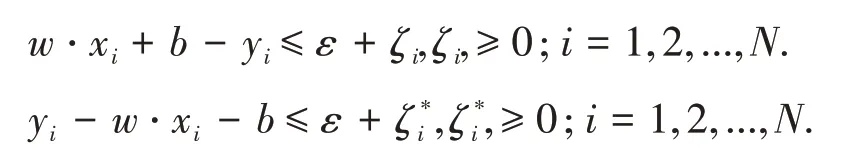
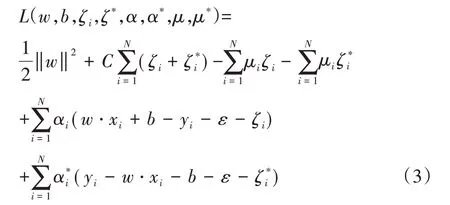
令L(w,b,ζi,ζ*,α,α*,μ,μ*)对w,b,ζi和ζ*i的偏导为零并代入式(3),可得:

支持向量机回归函数可以表示为:

可以用核函数代替内积,转换为:

式中: ),(ixxK表示核函数。
采用高斯径向基函数作为核函数,具体表示为:

最终的回归函数表示为:

2.2 建模的工作流程
(1)划分训练集和测试集
将所有样本集随机划分为训练集和测试集,其中训练集为总样本的80%(n=71),测试集为总样本的20%(n=18)。
(2)数据预处理
采用标准化方法对数据进行预处理,该方法可以加快收敛速度,解决数据无量纲化的问题。

式中,x′(i)为第i个样本的标准化值;x(i)为第i个样本的实际值。为总样本的平均值;σ为总样本的标准差。
(3)根据训练集建立支持向量机模型,选择模型评价指标
选用均方误差(RMSE)和决定系数(R2)来评价后测执行控制缺失值预测模型的性能。
RMSE表示为:

式中,m为样本总数,y为实际值,y′为预测值。RMSE越接近零模型性能越高。
R2表示为:

式中,y为实际值,y′为预测值为实际值的平均值。R2越接近1表示模型性能越高。
(4)使用网格搜索确定模型最优参数
网格搜索通过交叉验证方法,将估计函数中每一个参数的所有可能取值都分别生成一个列表,然后把每个列表中的值都进行组合,所有的组合结果就生成了“网格”,以此将学习算法优化至最佳。在拟合函数尝试了所有的组合结果后,返回一个最合适的学习器,自动调整至最佳参数组合。
(5)输入测试集对后测执行控制缺失值预测模型的性能进行测试和分析。
综上可知,建立基于机器学习的后测执行控制缺失值预测模型的工作流程如图1所示。

图1 后测执行控制缺失值预测模型的工作流程Fig.1 The workflow of prediction model of missing values on executive control at post-test
3 结果
执行控制的评价指标是不一致条件下的平均反应时减去一致条件下的平均反应时得出的差值。因此,执行控制的缺失意味着一致条件下的平均反应时或者不一致条件下的平均反应时存在缺失。本研究将执行控制缺失值的预测模型分为一致条件下的平均反应时预测模型和不一致条件下的平均反应时预测模型,通过这两个模型更加细致精确地预测执行控制的缺失值。此外,为了展现出后测执行控制缺失值预测模型的优越性,选择插补方法中常用的回归替换法和均值替换法与预测结果进行对比。
3.1 一致条件下的平均反应时预测结果
图2为预测模型对测试集数据中一致条件下的平均反应时预测的结果。从图2可以看出,一致条件下的平均反应时的实际值和预测值有多点近乎重合,相差很小。预测模型获得了理想的预测结果,验证了该模型的有效性。
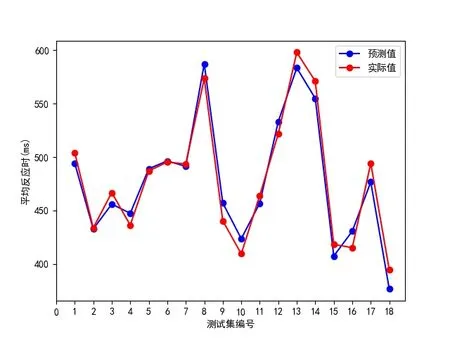
图2 一致条件下的平均反应时预测结果Fig.2 The predicted results of average reaction time under congruent conditions
表1为预测模型、回归替换和均值替换三种方法对一致条件下的平均反应时缺失值进行处理后的结果对比。从表1可以看出,预测模型方法的最大绝对误差为20.86 ms,最大误差率为4.87%,平均绝对误差为11.32 ms,平均误差率为2.41%,都低于回归替换法和均值替换法。回归替换法的各项误差指标全部低于均值替换法。

表1 不同方法处理一致条件下的平均反应时缺失值的结果比较Table 1 Comparison of the results of the missing values of the average reaction time under congruent conditions by different methods
3.2 不一致条件下的平均反应时预测结果
图3为预测模型对测试集数据中不一致条件下的平均反应时预测的结果。从图3可以看出,不一致条件下的平均反应时的实际值与预测值同样相差很小,拟合效果很好。预测模型可以描述测试集中数据的变化趋势。

图3 不一致条件下的平均反应时预测结果Fig.3 The prediction result of average reaction time under incongruent conditions
表2为预测模型、回归替换和均值替换三种方法对不一致条件下的平均反应时缺失值进行处理后的结果对比。从表2可以看出,预测模型方法有着很大的优越性,其最大绝对误差为44.54 ms,最大误差率为7.19%,平均绝对误差为16.6 ms,平均误差率为3.02%,在各项误差指标上都比回归替换方法和均值替换方法低。当数据发生较大的波动时,均值替换法不能很好描述这种变化趋势,从而产生了较大的绝对误差。

表2 不同方法处理不一致条件下的平均反应时缺失值的结果比较Table 2 Comparison of the results of the missing values of the average reaction time under incongruent conditions by different methods
3.3 模型评价指标
表3为一致条件下的平均反应时预测模型和不一致条件下的平均反应时预测模型的RMSE和R2。结果表明,两个模型的决定系数分别达到0.96和0.95,都大于0.85,这证明两个模型都很可靠。因为一致条件下的平均反应时实际样本值本身较小,所以在决定系数相差不大的情况下,不一致条件下的平均反应时预测模型的均方误差高于一致条件下的平均反应时预测模型的均方误差。

表3 模型评价指标Table 3 Model evaluation index
4 结论
本研究以运动对大学生执行控制影响的纵向研究为例,提出和验证了一种基于机器学习的纵向缺失值处理新方法,可以有效地解决体育科学研究中的后测数据缺失值问题,为今后机器学习应用于体育科学研究中的后测数据缺失值处理提供了实践基础。
