风速对单双层着装状态下运动服针织面料湿阻的影响
2021-07-26王利君马希明丁殷佳陈诚毅
王利君, 马希明, 丁殷佳, 陈诚毅
(1. 浙江理工大学 服装学院, 浙江 杭州 310018; 2. 浙江省服装工程技术研究中心, 浙江 杭州 310018)
运动服作为运动时人体与环境间的中间层,对二者之间的热湿传递起着十分重要的作用。作为服装热湿传递性能的重要评价指标,热阻和湿阻常用于构建人体与环境间的热湿传递模型,从而评价服装的热湿性能[1-3]。服装的热阻和湿阻受多种因素影响,包括服装自身的款式、着装层数、衣下间隙、风速以及人体运动及服装面料自身的性能等[4-6]。
服装的热阻、湿阻由面料自身和表面边界空气层的热阻、湿阻组成,风速的增加会扰乱面料内部和边界的空气层,从而改变服装的热湿传递性能。于瑶等[7]研究表明,当人体静止站立时,热阻随风速的增大而减小。Havenith等[8]选择了3套正常工作服,测试了在有风状态(风速为0.7,4.1 m/s)下的热阻值,并得出了针对有风条件下的正常工作服的热阻修正方程。Nilsson等[9]针对冬季防寒服在0.4~1 m/s风速下的热阻值展开了研究,得到了相关的修正方程。王发明等[10]利用暖体假人“Walter”测量了各层服装及不同组合的热阻,结果显示单件服装热阻与服装组合系统的热阻之间呈近似指数关系。赵蒙蒙等[11]研究表明,通风系统的引入可有效减少服装的湿阻。Cui等[6]研究发现,风速的提高极大程度上降低了服装的湿阻。上述研究内容主要集中在风速与单层面料热阻、湿阻的关系上;但运动服双层的着装方式在日常生活中非常普遍,不同的服装组合后的湿阻也不同,并且很多室外运动往往是在有风的环境下进行,因此,研究风速对面料湿阻的影响以及单双层着装状态下面料湿阻之间的定性定量关系,对于指导企业和消费者合理搭配运动服装,提高运动套装舒适性具有重要意义。
本文通过对4种风速下12种T恤面料、8种外套面料以及聚类分析后两两组合的9种双层组合运动服面料的湿阻进行测试,模拟皮肤-T恤-外套之间的透湿传递过程,分析软风范围内风速(0.1~1.5 m/s)与单、双层组合运动服面料湿阻间的定量关系。
1 实验部分
1.1 试样与仪器
选用20种市场上常见的运动服针织面料。1#~12#为T恤面料、13#~20#为外套面料,具体规格参数见表1。
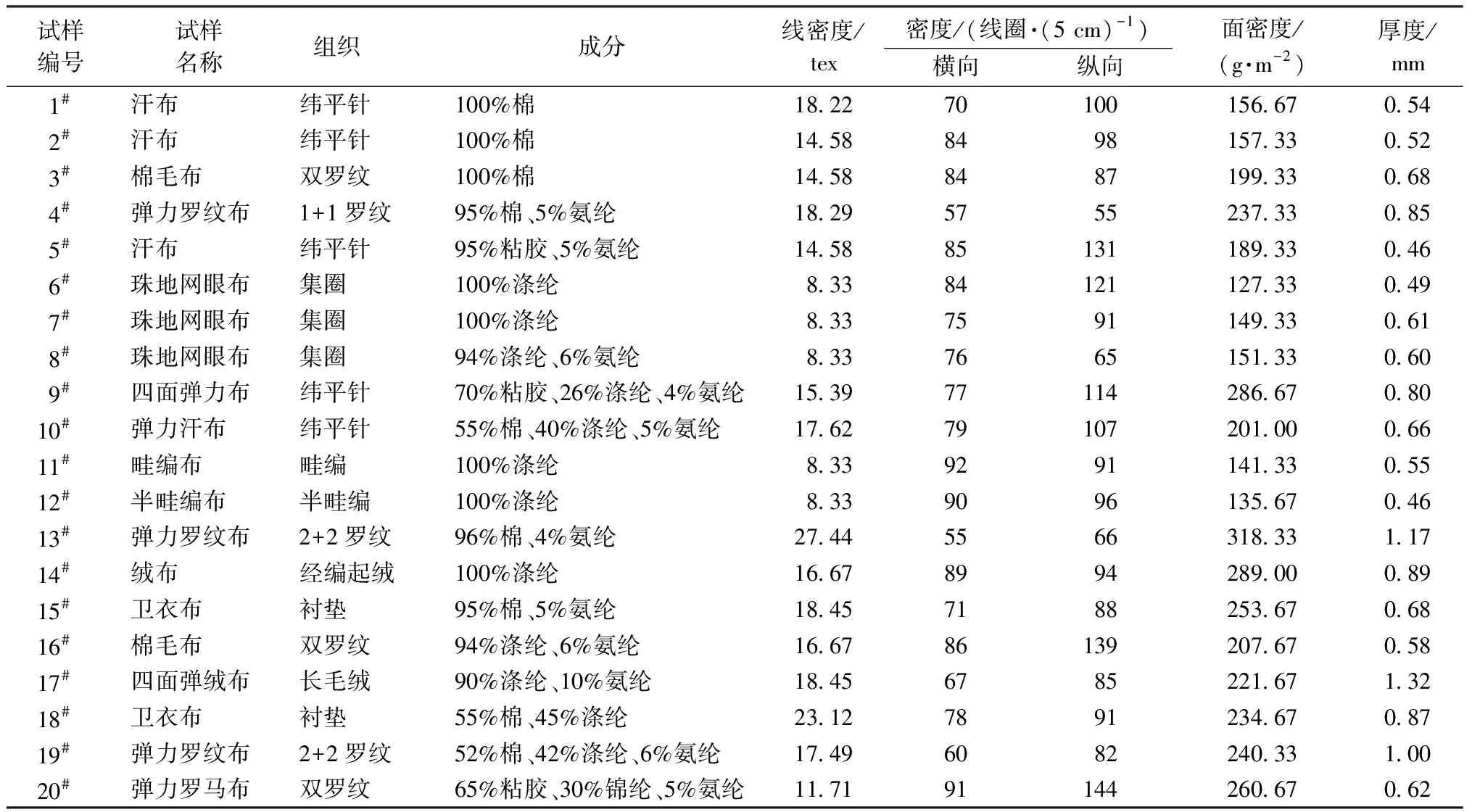
表1 织物规格参数表Tab.1 Fabric specification parameters
电子天平(沈阳龙腾电子有限公司)、YG(B)141D型数字式织物厚度仪(温州方圆仪器有限公司)、YG(B)216-Ⅱ型织物透湿量仪(温州大荣纺织仪器有限公司)、YG(B)871型毛细管效应测定仪(温州大荣纺织仪器有限公司)、Y511型织物密度分析镜(温州方圆仪器有限公司)、YG461-III型数字式织物透气量仪(温州大荣纺织仪器有限公司)、DST52008纺织品干燥速度测定仪(大荣科学精器制作所)、SGHP-10.5服装热阻和湿阻检测系统(美国西北测试科技公司)。
1.2 织物性能测试
1.2.1 舒适性
测试前根据GB/T 8629—2001《纺织品 试验用家庭洗涤和干燥程序》和GB/T 6529—2008《纺织品 调湿和试验用标准大气》对所有试样进行预处理和调湿。在温度为(20±2)℃、相对湿度为(65±2)%的条件下,根据FZ/T 01071—2008《纺织品 毛细效应试验方法》、GB/T 21655.1—2008《纺织品 吸湿速干性的评定 第1部分:单项组合试验法》、GB/T 12704.1—2009《纺织品 织物透湿性试验方法 第1部分:吸湿法》和GB/T 5453—1997《纺织品 织物透气性的测定》,测得织物芯吸高度、干燥速度、透湿率和透气率,如表2所示。

表2 织物性能参数Tab.2 Fabric performance parameters
1.2.2 湿 阻
采用服装热阻和湿阻检测系统和自制网架隔层对单、双层组合运动服针织面料进行湿阻测试。为更好地模拟双层着装状态,本文搭建网架隔层支撑外层织物,见图1。

图1 自制网架Fig.1 Self-made net frame
传统平铺式测量方式因重力因素使双层织物间空气层厚度接近于零,实际由于体温和衣下间隙,2层织物间存在空气层。为研究风速对湿阻的影响,结合实验操作的简易性,测试时内外层织物的空气层厚度取7 mm[12]。具体搭建方案如下:首先在内层织物上方使用4根高7 mm、长50 cm的亚克力边框板围1圈,然后在其上方放置由直径为1 mm的铁丝两两间隔2 cm编制成的铁丝网,最后将测试所需的外层织物平铺于铁丝网上。
为保证环境箱内风速的稳定性和精确性[13],本文针对软风级别的风速范围,选定0.1、0.5、1.0、1.5 m/s 4种风速作为测试风速,实验过程中风速可精确至±0.05 m/s。实验开始时根据ISO 11092—2014《纺织品 生理效应 稳态条件下耐热和耐水蒸气性能的测量(防护热板排汗试验)》中湿阻测试要求设置环境箱,温度为(35±0.1) ℃,湿度为(40±3)%,热板温度为(35±0.1) ℃,环境箱提前预热至稳态。然后将已备好的大小为50 cm×50 cm的单层面料或双层网架隔层面料正面朝上平铺于玻璃纤维薄膜之上,风速传感器末端调节至织物中上方7 mm处,每次测试需保持稳定状态30 min,最终得到的数据为30 min内湿阻的平均值。
2 结果与讨论
2.1 风速对单层织物湿阻的影响
为定量分析T恤面料和外套面料在不同风速下湿阻的变化,参照ISO 11092—2014标准,将风速为1.0 m/s时的面料湿阻定义成标准湿阻,作为各面料湿阻变化的参照值,绘制4种风速下T恤面料和外套面料湿阻、标准湿阻与风速的三维关系图,如图2所示。
从图2中4种风速下T恤面料的湿阻可以看出:1)总趋势上,在软风范围内,T恤面料湿阻随风速的增大而减小。当风速从0.1 m/s增加到0.5 m/s时,湿阻显著减小,当风速由0.5 m/s增加到1.5 m/s时,湿阻下降的速度开始趋于平缓。2)在风速变化相同的条件下,各面料湿阻减小的程度不同。
同理,对4种风速下外套面料的湿阻进行分析可知,外套面料湿阻的变化趋势和T恤面料相同。对单层运动服面料来说,当风速增大时,对流效应增强。一方面,导致空气密度减小,空气层变薄,水蒸气透过边界空气层的阻力减小;另一方面,空气的流动带走了织物内侧扩散的水蒸气,并以新空气替代,而新的空气流经织物表面又带走部分水气,以此循环,加快了织物水气的扩散,造成了湿阻的减小。
由图2可见,T恤面料和外套面料湿阻与风速和标准湿阻之间的关系并非简单的线性关系,因此尝试使用最小二乘法对数据进行多项式非线性拟合。为求得最佳多项式拟合结果,分别对数据进行一阶、二阶、三阶、四阶多项式拟合。
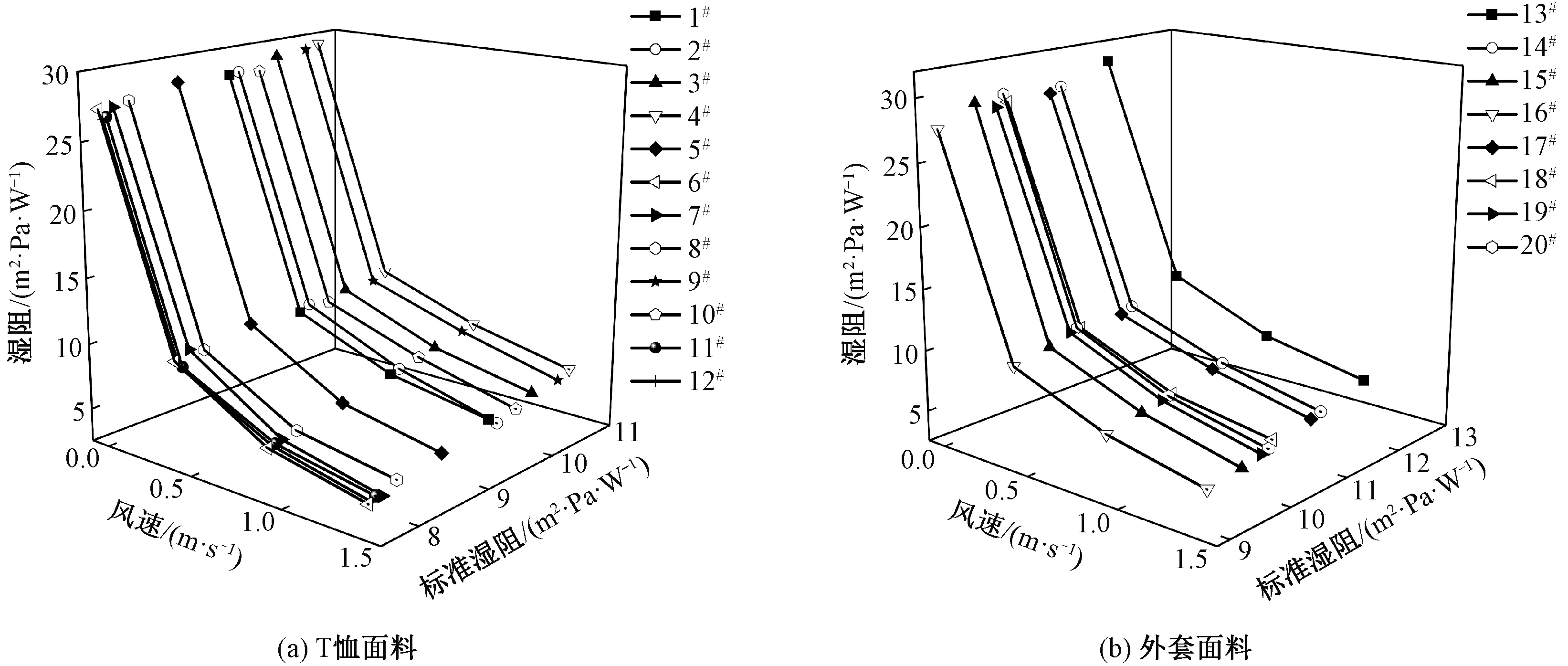
图2 4种风速下T恤面料和外套面料湿阻与风速、标准湿阻的三维关系图Fig.2 Three-dimensional relationship between moisture resistance and wind speed, standard moisture resistance of T-shirt fabric (a) and outwear fabric (b) under 4 kinds of wind speed
一阶:
f1(x,y)=k0+k1x+k2y
二阶:
f2(x,y)=k0+k1x+k2y+k3x2+k4xy
三阶:
f3(x,y)=k0+k1x+k2y+k3x2+k4xy+
k5x3+k6x2y
四阶:
f4(x,y)=k0+k1x+k2y+k3x2+k4xy+
k5x3+k6x2y+k7x4+k8x3y
式中:f(x,y)为湿阻,m2·Pa/W;x为风速,m/s;y为标准湿阻,m2·Pa/W;k0,k1,k2,k3,k4,k5,k6,k7,k8均为待定系数。计算不同阶数多项式拟合结果的均方根误差(RMSE)、平均绝对误差(MAE)、拟合优度(R2)和平均绝对百分比误差(MAPE),如表3所示。

表3 T恤和外套面料不同阶数多项式拟合结果Tab.3 Fitting results of T-shirt and outerwear fabrics with different order polynomials
由表3可见,随着多项式阶数的增加,拟合优度随之提高,但呈现出放缓趋势。尤其是阶数由三阶到四阶时,各项评价指标并没有明显的提高;但是拟合公式却变得更为复杂,计算量增加,因此,综合考虑公式的复杂程度和拟合优度问题,最终选择三阶多项式作为拟合公式。
T恤面料:
fT(x,y)=30.626+85.525x+0.620y+
72.289x2+0.065xy+25.589x3+
0.104x2y
外套面料:
fo(x,y)=32.567-83.733 4x+0.392y+
81.147x2+0.029xy-26.701x3+
0.144x2y
2.2 风速对双层组合织物湿阻的影响
2.2.1 聚类分析
为提高实验效率,需选出有代表性的T恤、外套面料,以模拟双层着装状态。依据影响湿阻变化的性能指标:透气率、透湿率、芯吸高度、干燥速率、标准湿阻(即本文中风速为1.0 m/s时所测得的湿阻),对12种T恤面料和8种外套面料分别进行Q型聚类分析。Q型聚类能将性质相近的面料分在同一类,把性质差异较大的分在不同的类,聚类结果见图3。
由图3可知,T恤面料可分为3类:{1#,2#,3#,4#,9#};{5#,7#,10#};{6#,8#,12#,11#},从中各挑选1种面料作为代表,即4#、10#、11#,将它们分别命名为A1、A2、A3。外套面料也可分成3类:{13#,14#,18#};{16#,20#};{15#,17#,19#},从中各挑选1种面料作为代表,即13#、16#、17#,将它们分别命名为B1、B2、B3。
2.2.2 风速对双层组合运动服面料湿阻的影响
将上述所选的代表性T恤面料和外套面料作为内外层,两两组合成9种双层组合织物。对4种风速下T恤-外套双层组合运动服面料的湿阻进行分析,结果如表4所示。
由表4可看出,风速对双层组合织物湿阻总的变化趋势和下降速度开始变平缓的转折点与单层织物相同。结合风速对单层织物的影响可发现,风对织物湿阻的影响主要是以下2个方面:一方面是由于风压作用,气流透入织物,扰乱了织物内部的空气层以及衣下空气层;另一方面是由于风使边界层空气变薄,边界层空气的湿阻值降低,从而使织物总的湿阻值降低。
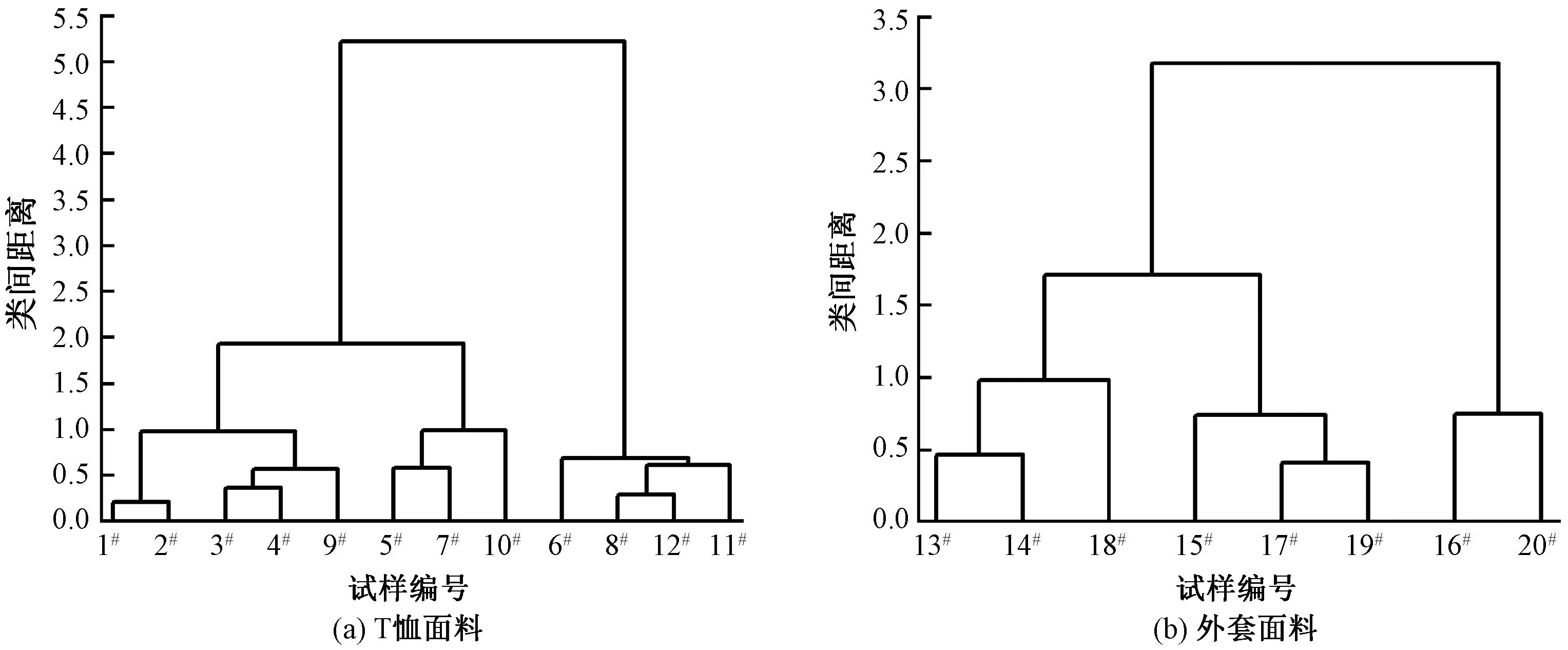
图3 T恤面料与外套面料聚类结果Fig.3 Clustering results of T-shirt fabrics (a) and outwear fabrics (b)
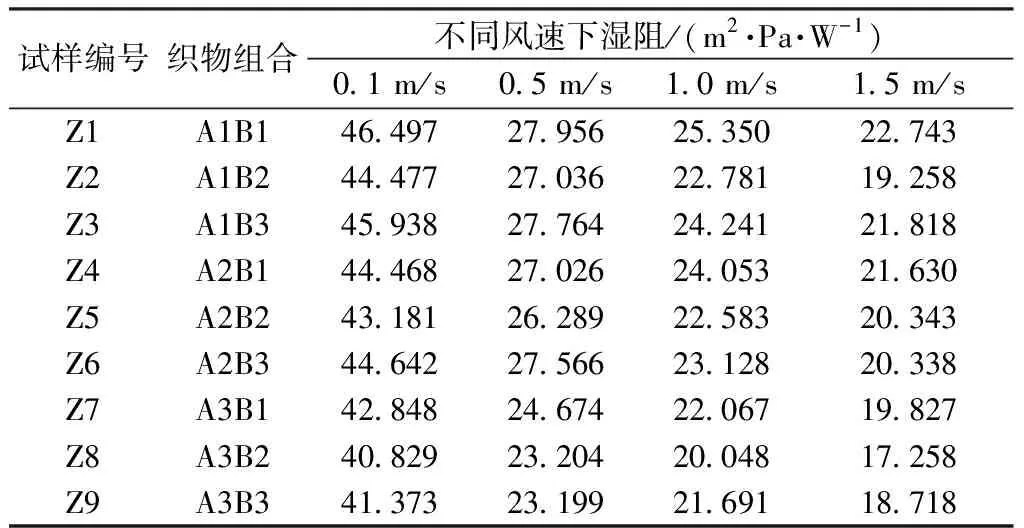
表4 风速对双层组合运动服面料湿阻的影响Tab.4 Effect of wind speed on moisture resistance of double-layers sportswear fabric combination
2.3 双层组合运动服面料湿阻预测模型构建
为进一步寻求风速、单层T恤湿阻、单层外套湿阻以及双层T恤外套组合运动服面料湿阻之间的关系,对风速和单、双层组合织物湿阻进行多元贝叶斯回归分析。
1)针对双层组合织物湿阻建立多元贝叶斯回归模型:
Y=β0+β1X1+β2X2+β3X3+ε
式中:X1,X2,X3分别表示双层组合织物的内层织物湿阻、外层织物湿阻以及风速;β1,β2,β3为其相应系数;β0为常数项;ε为不同风速下织物湿阻测试时的随机误差。
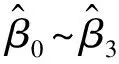
3)对预测模型进行检验,模型的拟合优度R2为0.988 4,平均绝对误差(MAE)为0.830 1,均方根误差(RMSE)为1.001 6,平均绝对百分比误差(MAPE)为3.20%。图4示出湿阻测试值与模型预测值的对比。
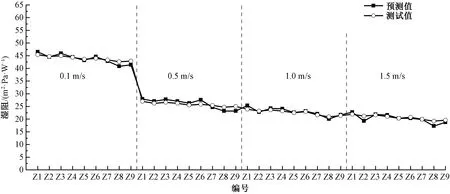
图4 湿阻预测值与测试值对比Fig.4 Comparison between predicted and output values
当平均绝对百分比误差低于20%时,可认为模型预测性良好[14]。此处模型的平均绝对百分比误差低于10%,与测试值相似度很高。这一结果表明,在软风范围内该模型能很好地利用单层面料的湿阻值预测双层组合面料的湿阻值,简化了实验过程,可以为企业选购运动服面料提供指导。
4)最终可确定软风范围内风速、T恤面料、外套面料以及T恤-外套双层组合运动服面料之间的湿阻模型:
Rdouble=13.293 3+0.807 3RA+
0.258 8RB-0.601 8v
式中:Rdouble为T恤-外套双层组合运动服面料湿阻,m2·Pa/W;RA为T恤面料湿阻,m2·Pa/W;RB为外套面料湿阻,m2·Pa/W;v为软风范围内风速,m/s。
通过对模型的分析可知,内层面料湿阻所占比重比外层面料的湿阻大,选择运动服套装时要格外注重T恤的散湿性能。
3 结 论
本文着重研究风速与单、双层组合面料湿阻之间的关系,为消费者和企业在外界软风范围的运动服着装和搭配提供参考意见。采用美国SGHP-10.5服装热阻和湿阻检测系统对市场上常用的12种T恤面料和8种外套面料进行了4种风速下的面料湿阻测试,并且通过聚类分析,选取3种T恤面料和3种外套面料为代表,利用搭建网架隔层模拟T恤和外套的双层着装状态,实现了定量测试不同风速下T恤与外套双层组合运动服针织面料之间的湿阻。研究结论如下:
1)在软风范围内(0.1~1.5 m/s),风速对单、双层组合织物湿阻总的影响趋势是相同的。当风速从0.1 m/s增加到0.5 m/s时,湿阻均随风速的增加显著减小;当风速由0.5 m/s增加到1.5 m/s时,湿阻的下降速度均开始趋于平缓。
2)在软风范围内,分别构建了单层面料(T恤或外套面料)湿阻与风速间的三阶多项式模型,以及双层组合面料湿阻与内外层面料湿阻之间的线性模型。2个模型均具有良好的预测性,平均绝对百分比误差都在5%以内。
3)通过对双层组合运动服面料湿阻模型的分析发现,内层T恤面料的湿阻对双层组合运动服面料湿阻的影响更大,着装时要格外注重T恤的散湿性能。
