基于模拟退火算法改进遗传算法的织物智能配色
2021-07-26许雪梅
许雪梅
(浙江理工大学 信息学院, 浙江 杭州 310018)
织物智能配色是利用计算机配色系统速度快、工作效率高的优点进行颜色配方的智能预测[1],并且能够根据配方预测颜色。织物智能配色的核心部分是配色算法,智能配色算法能够实现又快又准地配色[2],大大减少打样的次数。
目前织物配色应用最广泛的理论基础是Kubelka-Munk理论[3-4],该理论在色纺纱配色算法中应用较多[5-6]。一些研究人员引入人工智能技术如神经网络到配色算法中[7],神经网络在纺织品的染色配色上已有不少成功的应用[8-9],例如:肖春华[10]将深度学习技术中的深层神经网络应用到织物智能配色算法中;CHAOUCH Sabrine等[11-12]将蚁群算法应用于织物颜色的配方预测,有效地获得了织物的颜色配方预测思想的元启发式技术。配色精度、收敛速度和泛化能力等问题一直都是织物智能配色技术不断改进优化的方向。
本文利用基于BP神经网络的遗传算法进行织物颜色配方智能预测,并引入模拟退火算法对遗传算法配方预测模型进行优化。
1 配色模型构建
1.1 遗传算法配色模型构建
基于遗传算法的织物配色智能预测模型中,初始种群是随机生成的,包含了所有可能的配色方案。假设种群中的每个个体都由一条染色体组成,织物智能配色的解决方案用一个染色体定义,然后用有限长度的字符串来编码染色体,配色预测要求算法精度高且搜索范围大,所以选择浮点数编码方法进行编码,每条染色体上的基因个数由所用染料的种类数决定,每个基因值代表每种染料的浓度。
1.1.1 遗传算法适应度函数构建
应用遗传算法进行织物智能配色的核心问题就是适应度函数的选择,其对于个体能否进入下一代起着决定性的作用。在实际应用中,要计算出一个给定标样的染料的配方浓度,就要不断缩小给定的标样与所染出的试样之间的色差值。本文提出用BP神经网络和最新色差公式CIEDE2000结合作为遗传算法的适应度函数,由事先训练好的BP神经网络模型进行色度值L、a和b值的预测,再根据色差公式计算色差值。适应度函数公式为
(1)
式中:ΔE00为本文研究所提出的配色算法预测的颜色与标准样本颜色之间的色差值,ΔE00越小,f(x)越大,说明个体的适应能力越强;δ是为了避免被0整除而设置的一个常数,通常设为10-6。
1.1.2 遗传操作
1)选择。使用的是无回放随机选择,即随机选择运算是由每个代表着配色解决方案的的生存期望值所决定的,该值通过个体在下一代群体中由式(2)计算所得。
(2)
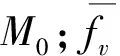
2)交叉。由于选择的基因编码方法是浮点数编码,因此选择算术交叉方法,2个新个体的产生是依据进行线性组合的2个包含有配方信息的个体所得,式(3)为线性组合的计算公式。
(3)
式中:G1、G2分别代表2个染色体;k1、k2为乘子,选择扩展中间交叉,即k1,k2∈[-0.5,0.5]。
3)变异。采用非均匀变异的方法,对原有的基因值做一随机扰动,以扰动后的结果作为变异后的新基因值。
1.2 模拟退火算法改进遗传算法
在遗传算法的预测过程中增加模拟退火算法的判断,防止遗传算法在预测过程中陷入局部最优解,导致最终输出结果不是全局最优配色方案。在遗传算法进行配色智能预测的过程中,由于变异产生的新配色个体是完全随机的过程,所以在算法爬坡的过程中容易陷入局部最优解,导致梯度消失,加入模拟退火算法会在迭代的过程中修正变异概率,解决梯度消失问题,找到全局最优解,变异概率修正函数如式(4)所示。
(4)
(5)
式中:P为模拟退火过程中突跳概率;T为当前温度值;E(n)为能量,在本文中E(n)=ΔE00;E(n+1)为下个节点的能量;ε为[0,1)区间的随机值;T(0)为初始温度值;t为迭代次数。
1.3 算法步骤
1)设置基本参数:种群规模、迭代次数、交叉与变异概率以及初始温度等。
2)种群初始化:随机产生大规模种群,依据所用染料浓度值的范围对初始化的种群进行编码。
3)利用BP神经网络预测颜色,计算色差,根据色差计算遗传算法预测出的每个配方的适应度函数值。
4)模拟退火算法操作。根据模拟退火算法中的温度函数公式计算突跳概率,并将该概率值作为遗传算法的变异概率。
5)判断是否满足模拟退火终止条件,若不满足,则缩小变异范围,继续执行遗传操作;若满足,则直接执行遗传操作。
6)根据新参数进行遗传变异、交叉与选择操作,生成子代种群,再转到步骤3)继续迭代运行。
7)检查是否满足终止条件,即达到规定迭代次数,若满足,则结束算法;若不满足,则转步骤4)继续迭代运行。
2 实验部分
2.1 材料与染色及测色方法
实验采用的基材织物为100%涤纶织物,经纬纱线密度分别为5.55、8.33 tex,面密度为75 g/m2,目前涤纶染色的主要染料是结构较简单、分子质量较低的分散染料,因此,实验选用分散红3B、分散黄RGFL、分散蓝2BLN三原色染料。
采用母液法配制染液。配制高浓度的分散红3B、分散黄RGFL、分散蓝2BLN 3种母液,质量浓度为5 g/L。在配制样本液的过程中对母液进行稀释得到实验样本的染液,织物质量为10 g,浴比为1∶20,采用高温高压法对织物进行染色。
染色样品的光谱反射率用X-Rite Ci7800台式分光光度仪在D65光源、10°视角下测量,测色孔径为25 nm,包含紫外光,选择包含镜面反射光(SCI),不考虑物体表面的光泽影响,测量的是物体真实色。测量的样品光谱反射率在360~750 nm波段内,间隔为10 nm。每个样品折叠2次,呈现总共4层的织物,以获得足够的不透明度。随后在多个位置进行一系列颜色测量,每个样品测量3次,以使实验所用织物的光谱反射率测量误差最小化。
2.2 实验数据准备
3种染料质量分数选择范围为0.05%~3.00%,从而形成了一个包含大量不同染色样本的数据库。使用18个不同的三元混色物作为标准颜色样本,标准样本颜色配方及色度参数如表1所示。
2.3 适应度分析
BP神经网络根据算法预测的配方进行颜色的预测需要提前对网络进行训练,本文采用3层BP神经网络,输入层为3种染料用量,输出层为CIELab色度值,以确定最优的网络结构与参数,使适应度函数的评价更为准确。基于已有的实验数据对BP神经网络进行了训练,并选择标准样本数据对训练出的网络进行验证,BP神经网络根据标样配方预测出的颜色与标准样本颜色之间的色差值为理论色差值,该网络预测的标准样本的CIELab色度值和理论色差值如表2所示。
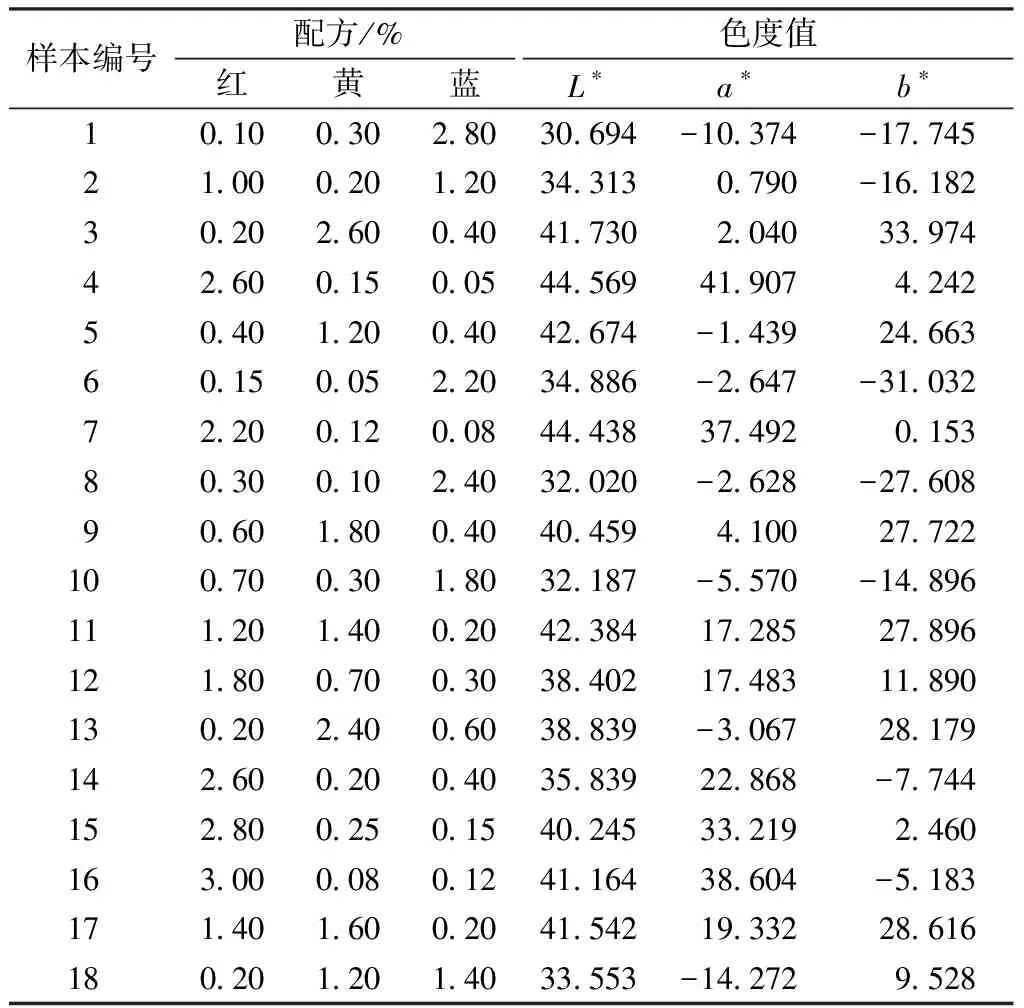
表1 标准样本颜色配方和色度参数Tab.1 Color formula and chromaticity parameters of standard samples

表2 BP神经网络验证结果Tab.2 Validation results by BP neural network
通过分析表2可知,训练出的BP神经网络能够根据算法预测出的配方值实现颜色预测,预测的理论色差值整体较小,均小于0.300,色差均值为0.165,表明色差预测效果优良,证明该模型适用于织物的颜色预测,为之后与遗传算法和模拟退火算法结合进行配方预测奠定了基础。
3 实验结果与分析
3.1 算法性能分析
对基于模拟退火算法改进遗传算法的配色预测算法进行了多次实验,修改算法的迭代次数和种群规模大小来对算法的收敛性能进行分析,实验结果如表3所示。
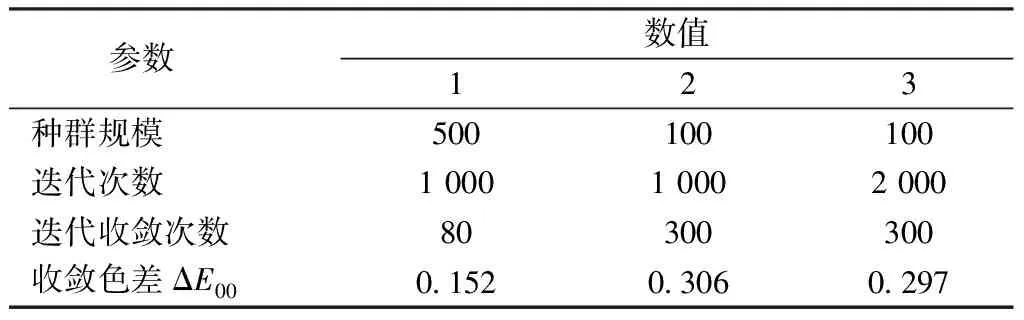
表3 算法训练收敛性分析Tab.3 Convergence analysis of algorithm training
通过分析表3可以看出,种群规模设置为500,迭代次数设置为1 000时,算法收敛速度最快,迭代80次即可收敛,收敛色差最小(0.152),也即个体的适应度函数值最大,此时算法性能最优,适用于织物颜色配方的智能预测。
3.2 配方预测结果与分析
上述算法仿真实验结果获得的配方即预测配方及其与标准样本颜色配方之间的绝对误差Ea如表4所示,绝对误差公式为
Ea=|Cp-Ca|
(6)
式中,Ca和Cp分别为配方的实际浓度和预测浓度。
通过分析表4可发现,由模拟退火算法改进基于BP神经网络的遗传算法(GA-BP-SA算法)预测的配方与实际配方较为接近,绝对误差值较小,整体小于0.100 0,三原色的绝对误差平均值分别为0.008 8、0.011 1和0.012 1,证明该模型具有良好的织物颜色配方预测功能。

表4 GA-BP-SA算法预测结果Tab.4 Results predicted by GA-BP-SA algorithm
3.3 染色实验结果与分析
为了验证本文提出的配色预测模型的实用性,使用根据模拟退火算法改进遗传算法的配色模型预测的颜色配方进行染色实验,根据测量染色试样的反射率计算CIELab色度值及各分量色差值,结果如表5所示。

表5 染色样本CIELab色度值和各分量色差值Tab.5 CIELab chromaticity value and color difference value of each component of stained sample
本文采用的CIEDE2000色差公式是基于CIELab 色差公式的基础上发展而来的,与CIELab色差公式相对应的色彩空间为L*a*b*均匀颜色空间,均匀颜色空间对配色评价非常重要,其主要是对颜色空间中的彩度差ΔC*、明度差ΔL*、色度差Δa*和Δb*及色相差ΔH*进行分析,其中明度差和色度差是对染色试样和标准样本测量值的比较,可简单直接地显示颜色误差,如表6所示。彩度差代表染色试样与标准样之间颜色鲜艳度差异,色相差代表染色样本与标准样之间的色相角度差异,通过这些分量色差能够反映人眼对颜色差异的真实感觉,通过偏移规律可判断染色样品与样本的接近程度,结合表5可以看出,各分量色差值整体较小,表明染色样本与标准样本的颜色具有良好的一致性。

表6 分量色差偏移规律Tab.6 Shift law of component color difference
根据本文算法预测的配方染出的试样与标准样本之间的色差值也即实验色差值,为计算其值,对不同的色差公式进行综合比较后,选择了能够进一步改善色差视觉一致性的CIEDE2000色差公式进行,结果如表7所示。
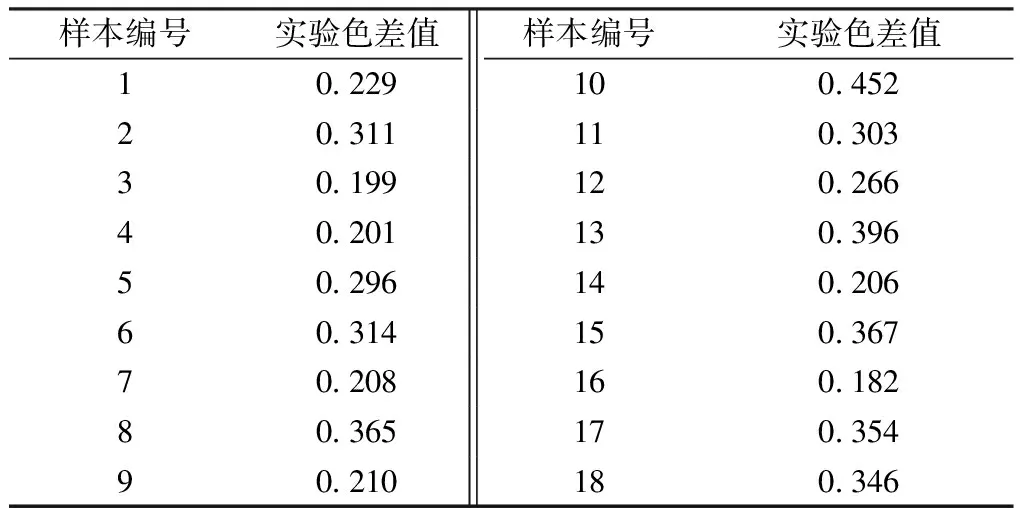
表7 染色样本与标准样本之间的实验色差值Tab.7 Experimental color difference between dyed sample and standard sample
由表7可知,由GA-BP-SA算法预测的配方进行染色实验获得的染色试样和标准样本之间的实验色差值整体小于0.500,平均色差值为0.289。通过分析表8所显示的色差分布来看,ΔE≤0.4的情况已经包含了绝大部分,染色获得混色样和标准样的实验色差均在可接受范围内,色差计算结果与目视评判具有良好的一致性,表明所建立的织物配方智能预测模型实用性优良,具有良好的实际应用价值。

表8 GA-BP-SA算法配色精度分析Tab.8 GA-BP-SA algorithm color matching accuracy analysis
3.4 泛化能力验证
为验证所提出GA-BP-SA算法的泛化能力,随机选取了训练样本之外的18个样本进行实验。由色差公式CIEDE2000计算的18个染色样本的理论色差值和实验色差值如图1所示。

图1 验证样本理论色差值和实验色差值Fig.1 Theoretical color differences and experimental color differences of verify samples
从图1可以看出:由GA-BP-SA算法预测的配方拟合颜色色差不仅集中,而且总体较小,由仿真实验所得的理论色差主要分布在0.179~0.276之间,中位数为0.240;由染色实验获得的实验色差主要分布在0.383~0.498之间,中位数为0.437。显然,基于GA-BP-SA算法的配色模型预测的配方所染出的颜色和标准样颜色不仅高度符合,并且泛化能力也很好。
4 结 论
本文融合遗传算法和模拟退火算法,结合BP神经网络对织物智能配色进行研究。分别从理论色差、实验色差和配方误差3个方面验证了本文提出的智能配色算法的合理有效性,并验证了该算法的泛化能力。结果表明,模拟退火算法改进基于BP神经网络的遗传算法能够较好地实现织物颜色预测与配方预测。模拟退火算法改进的遗传算法在求解织物智能配色问题上具有一定的应用价值,不仅能够提高配色精度、效率以及泛化能力,而且优化了配色过程,有着良好的应用前景,对推进计算机智能配色发展,提高染色生产效率具有一定的意义。
