基于 Super-twisting算法的永磁同步电机直接转矩控制
2021-07-26李少朋贺耀庭
李少朋,谢 源,张 凯,贺耀庭
(上海电机学院 电气学院,上海 201306)
0 引言
永磁同步电机具有调速范围广、控制结构简单、动态响应快、鲁棒性强等特点[1],因此,广泛应用在风力发电领域。目前,常用矢量控制和直接转矩对永磁同步电机进行控制。矢量控制是通过对变流器的空间电流(电压)的控制,满足永磁同步电机所需电压电流,达到控制效果。直接转矩控制(DTC)采用滞环比较器实现对转矩和磁链的直接控制,具有控制结构简单、转矩动态响应良好等优点[1]。但传统的DTC存在磁链和转矩脉动大、高频噪声等问题。
为解决DTC转矩的脉动问题,文献[1]对开关频率不恒定和转矩脉动大的缺点,提出了一种恒定开关频率的直接转矩控制方法,在传统的直接转矩的基础上,增加PI转矩控制器和载波比较器,实现逆变器的开关频率恒定,降低了转矩的脉动。文献[2]将电流斩波与DTC方法相结合,通过对应参数的选择降低转矩脉动。文献[3]从定子电阻补偿的角度对计磁链进行精确计算,通过将优化后的定子电阻作为估算磁链的参考值,并将模糊控制和PI控制相结合,限制了系统中定子电阻变化对控制的影响,降低了转矩脉动。文献[4]使用混沌蚁群算法对PI控制器参数整定,通过对PI参数的优化,使得系统中电机的转矩和磁链的脉动有所降低,但效果不佳。文献[5]将零矢量引入到转矩调节器中,并对转矩调节器进行了定量的优化设计,将其应用到DTC中,使得磁链脉动和转矩脉动有较大程度的降低。文献[6],[7]提出了一种由SVPWM调制的直接转矩控制方案。该方案解决了DTC过程中的开关频率不稳定的问题,优化了控制结构,但系统控制依赖电机参数的变化,对于系统参数变化敏感即鲁棒性较差。本文将Super-twisting滑模变结构与SVPWM矢量控制技术相结合,提出一种二阶滑模控制的直接转矩控制方法。该方法具有SVPWM控制的优点,保证了开关频率的稳定,并针对SVPWM控制的缺点通过滑模结构进行优化,使得系统控制的鲁棒性增强。仿真结果表明,采用二阶滑模直接转矩控制方法有很好的跟踪性能和抗负载扰动能力,使得转矩脉动大大降低,提高了系统的稳定性和响应速度。
1 永磁同步电机的数学模型
本文以三相表贴式永磁同步电机(Surface Permanent Magnet Synchronous Motor,SPMSM)为研究对象,忽略了电动机的铁芯饱和、磁滞、涡流损耗等影响因素,永磁同步电机的dq轴定子电压方程为[9]~[12]

对于三相表贴式的永磁同步电机,定子电感满足Ld=Lq=Ls,则此表贴式永磁同步电机模型的电磁转矩方程为

式中:ud,uq为定子电压在d-q轴上的分量;id,iq为定子电流在d-q轴的电流分;ψd,ψq为定子磁链在d-q轴上磁链分量;ωe为电角度;R为定子电阻;Ld,Lq为定子电感在d-q轴分量;ψf为转子磁链;pn为极对数。
2 基于二阶滑模控制器设计
2.1 Super-twisting滑模变控制理论
Super-twisting算法的滑模作为一种高阶滑模算法,其本质是二阶滑模算法,并不需要滑模变量的导数,从而使得控制结构简化[11],[10]。Supertwisting滑模控制包含不连续的滑动变量函数和连续的导函数。Super-twisting算法的一般形式为[11]

式中:x1,x2为状态变量;λ,α为正常数;ρ1,ρ2为扰动;r的取值决定滑模动态结构,r取值为0≤r≤1。
当r=0.5时,系统可以达到最大的二阶滑模动态。为了抑制抖振现象,本文将Super-twisting算法中符号函数sign()替换为饱和函数sat()。
对于控制器的输出量和输出量的二阶导数,其表达式为

式中:y为输出量;x为状态变量;H,G为输出量y的二阶导数的上限和下限。
Super-twisting滑模控制器不需要滑模变量的导数,在滑模面上收敛和稳定性的充分必要条件为

式中:HM≥|H|;GM≥G≥Gm。
由式(6)可以得出ka,kb参数。
2.2 二阶滑模控制器设计
为得到磁链控制器的表达式,定义磁链的滑模面函数为

由Super-twisting算法的二阶滑模控制理论得出磁链控制器的表达式为

设定子磁链的ψs幅值为常数,则此时的电磁转矩Te为

为获得转矩控制器的表达式,定义转矩的滑模面函数为

由Super-twisting算法的二阶滑模控制理论得出,转矩控制器的表达式为
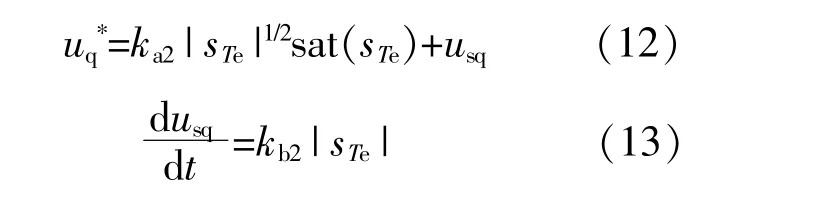
由式(12),(13)可知,两个观测器中的ka1,kb1,ka2,kb2为待设计参数,其值都大于0。
2.3 待设计参数整定
对式(1)~(3)进行坐标变换,根据坐标变换原理则永磁同步电机的数学模型在xy轴数下的定子电压方程为

式中:ψs为定子磁链;ψx,ψy为定子磁链在xy坐标轴的分量;δ为转子磁链ψf与定子磁链ψs的夹角,该角即为转矩角。
令ψs=ψx,定子磁链可表示为

式(21),(22)中所有参量均为有限值,故H,G也为有限值。结合式(6)可以很好地设计转矩控制器中的参数ka2,kb2。本文取的参数值为ka1=100,kb1=876,ka2=100,kb2=217。
3 滑模函数稳定性证明及鲁棒性分析

将式(7),(16)和(10),(11)分别带入式(24)可得:

由式(25)可知,Super-twisting二阶滑模算法在有限的时间内是收敛的,满足李雅普诺夫函数的达到条件。
系统在实际的运行过程中会受到外部的干扰,受干扰的磁链和转矩方程为

4 实验仿真及结果分析
为验证上述理论的正确性及控制方法的有效性,在Matlab/Simulink仿真环境下,对系统进行了建模与仿真分析研究。图1为控制框图。

图1 控制框图Fig.1 Control block diagram
由图1可知,二阶滑模直接转矩控制方法中首先获取逆变器输出的电压电流值。将提供给永磁同步电机的电压、电流值在dq坐标系下分解得到其dq轴分量。根据电压、电流和定子磁链的关系式,经计算得到永磁同步电机定子磁链在d轴坐标的幅值,将其作为运行过程中的实际值。通过外部给定的期望磁链值与实际值做差,将差值作为磁链滑模控制器的输入,经过滑模控制函数得到控制输出值。对于转矩控制器,将永磁同步电机的转速与给定转速通过PI调节得出电磁转矩,将其作为外部给定值Te*。经上述的坐标变换过程,由式(1)计算出运行过程中的实际电磁转矩,使得给定电磁转矩与实际电磁转矩做差,输入方式与磁链控制器相同。图2为转矩和磁链的滑模控制结构框图。

图2转矩SMC和磁链SMC结构框Fig.2 Structure Diagram of sliding mode control
将上述控制得到的电压值,经反-park变换,将变换结果输入到SVPWM空间电压矢量控制器,得到相应的逆变器触发顺序,即可实现对电机磁链和转矩的直接控制。控制过程中对坐标变换、转子位置没有很严格的要求,控制过程简单。
为了验证上述理论的有效性,根据图1的控制框图,本文基于加拿大Opal-RT公司开发的一套工业级的仿真软件RT-LAB搭建了半实物仿真平台。在MATLAB/Simulink中搭建PMSM模型和逆变器模型,下载到RT-LAB中进行实时的仿真;控制部分采用DSP开发套件TM320F28335进行相应信号的采集,并通过控制算法输出的SVPWM控制RT-LAB中的PMSM,平台如图3所示。

图3 半实物仿真平台Fig.3 Semi-physical simulation platform
电机参数:极对数np=4,定子电感Ld=Lq=8.5 mH,定子电阻R=1.2Ω,永磁磁链ψf=0.175 Wb,转动惯量J=0.0008 kg·m2,粘滞摩擦系数B=0.0 01 N·m·s,额定转速为1 200 rad/min,额定电磁转矩TN=2 N·m,额定功率PN=600 W,额定电压UN=311 V。
为了验证磁链控制器和转矩控制器的跟踪精度、抗负载扰动能力和负载扰动后的恢复能力,本文给定转速n=600 r/min,电机在初始负载转矩为0,0.2 s后,负载转矩为1.5 N·m,SVPWM的频率设为5 kHz,仿真结果如图4所示。

图4 二阶滑模DTC策略和传统DTC策略转速波形图Fig.4 Second-order sliding mode DTCstrategy and traditional DTCstrategy rotate speed waveform
由图4可知,二阶滑模控制策略系统响应快,有超调,但很快跟随系统,动态性能好。突加负载时,转速有较小波动,转速在0.21 s时刻达到稳定。传统DTC策略响应过程也有超调,虽然比二阶滑模DTC超调低,但是其跟随系统的动态性能低于二阶滑模DTC策略,达到稳定运行状态所需时间长。突加负载时,转速有小幅度波动,并且达到稳定时为0.26 s,大于二阶DTC恢复时间。由此也说明了二阶DTC的动态性能好,提高了系统的动态性能和抗干扰性。实验波形与仿真结果吻合,验证了算法的准确性。
二阶滑模DTC和传统DTC转矩如图5所示。

图5二阶滑模DTC和传统DTC转矩波形图Fig.5 Torque waveforms of second-order sliding mode DTC and conventional DTC
由图5可知,在0.2 s时加入负载转矩扰动,转矩波动小并且迅速稳定达到所给定的转矩值,波动为1.2~1.8 N·m,稳定时间为0.011 s。实验波形与仿真结果相吻合。传统DTC在0.2 s时加负载转矩扰动,转矩波动较大,并且达到稳定的时间较长。转矩的波动为0.51~2.25 N·m,波动幅度较大。二阶滑模DTC方式可以有效的降低转矩脉动,并且可以迅速达到稳定,提高了系统的控制精度和系统的稳定性,二阶滑模控制对电磁转矩脉动的抑制效果较为明显。
二阶滑模DTC和传统DTC磁链如图6所示。

图6二阶滑模DTC和传统DTC磁链波形图Fig.6 Flux linkage waveforms of second-order sliding mode DTCand conventional DTC
由图6可知,磁链波动范围为0.008 Wb。二阶滑模DTC的磁链实验波形与仿真结果吻合。传统DTC磁链的波动范围为0.01 Wb。
5 结论
本文针对传统直接转矩控制中转矩脉动大、磁链脉动大和转速响应慢等缺点,设计了一种基于Super-twisting算法的二阶滑模直接转矩控制方法,并对二阶滑模控制的稳定性通过李雅普诺夫的判定定理加以证明。通过仿真实验得出以下结论:①二阶滑模的直接转矩控制方式采用转矩控制器和磁链控制器,有效减小了系统的高频抖动。使用SVPWM空间电压矢量调制,使得逆变器开关频率恒定的同时也降低了电机脉动;②二阶滑模直接转矩控制方法降低了控制过程中转矩和磁链的脉动。相对与传统DTC,本文提出的控制方法转矩脉动减少了65.11%,磁链脉动减少了20%,证明了本文提出方法的优越性;③二阶滑模直接转矩控制对于启动开始时,电机仍有一定的超调量。对于二阶滑模直接转矩的控制方法应该进行进一步的优化,使得超调量有所降低。
