弱电网低电压穿越期间并网逆变器系统的小干扰稳定性研究

张瑞强，李智玲，姚 骏，于 海，刘 远

（1.内蒙古电力（集团）有限责任公司 包头供电局，内蒙古 包头 014030；2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；3.内蒙古电力（集团）有限责任公司，内蒙古 呼和浩特 010020）

0 引言

风电、光伏等发电系统由并网逆变器接入电网。随着电网渗透率快速增加，交流电力系统对新能源场站的支撑作用在逐步弱化[1]。弱电网条件下并网逆变器系统的稳定问题已得到相关研究人员的广泛关注[2]。

目前，大多文献集中研究锁相环（Phaselocked Loop，PLL）对并网逆变器系统稳定性的影响[3]，然而，PLL与系统中其他控制环路、电网阻抗之间均存在着密切的耦合关系。尤其在弱电网条件下，多环节间的相互作用将导致系统的稳定性下降，引发系统振荡，甚至失稳，危害并网逆变器系统及其电网的可靠性和稳定运行能力[4]，[5]。文献[6]研究了PLL与电流控制环之间的交互作用对并网逆变器系统稳定性的影响，分析结果表明，PLL与电流环间的耦合作用将随着电网强度的降低而加剧。文献[7]基于三相并网逆变器的阻抗模型，利用广义Nyquist稳定判据分析了弱电网情况下PLL比例系数对系统稳定性的影响。文献[8]基于阻抗分析法建立了考虑PLL影响的三相并网逆变器输出阻抗模型，分析不同电网阻抗和PLL带宽与并网逆变器稳定性的内在联系。分析结果表明，增加电网阻抗和PLL带宽会导致PLL与电网阻抗耦合性增强，降低了系统的稳定性。文献[9]基于特征值分析法和时域仿真，研究了电网阻抗对并网逆变器系统电流内环控制器动态性能和稳定性的影响。分析及仿真结果表明，电网阻抗越大，逆变器并网控制系统越容易失稳，且其失稳表现和PLL与电流环之间的交互作用关系密切。

上述文献对并网逆变器系统小干扰稳定性的研究均是针对电网正常运行时。当电网发生短路故障时，并网逆变器系统将按照电网导则要求进入低电压穿越（Low Voltage Ride-Through，LVRT）控制模式[10]。但是，由于故障导致的电压骤降及无功电流的大量注入，使得控制系统与电网高阻抗的耦合作用加剧，并网逆变器更容易出现小干扰失稳问题。目前，并网电力电子设备在LVRT期间的小干扰稳定性尚未引起广泛关注[11]，[12]。文献[11]基于阻抗法分析了LVRT期间不同锁相环以及电流环带宽对DFIG动态稳定性的影响，表明LVRT期间DFIG更容易出现小干扰失稳。文献[12]通过复转矩法分析了锁相环和电流环交互作用对系统小干扰稳定性的影响。

本文建立了并网逆变器系统在低电压穿越期间的小干扰线性化模型，详细分析了电网阻抗、锁相环及电流环之间的耦合关系。采用特征值分析法对并网逆变器系统进行了全面的模态分析，得到了系统各个振荡模态的振荡特性，并通过根轨迹图分析不同系统参数对其小干扰稳定性的影响规律。在Matlab/Simulink中建立了并网逆变器的时域仿真模型，结合时域仿真验证了特征值分析结果的正确性。

1 低电压穿越期间并网逆变器系统的小信号模型

并网逆变器作为风电、光伏等新能源发电系统的并网接口，广泛采用“功率-电流”双闭环控制结构。当电网发生三相短路故障时，并网逆变器系统根据电网电压跌落程度直接向电网提供相应的有功、无功电流支撑[10]。典型的并网变流器拓扑及其在低电压穿越期间的控制系统如图1所示[8]。图中，ω1为额定电网角频率；igd，igq分别为系统输出电流的dq轴分量；utd，utq分别为逆变器系统端电压的dq轴分量。

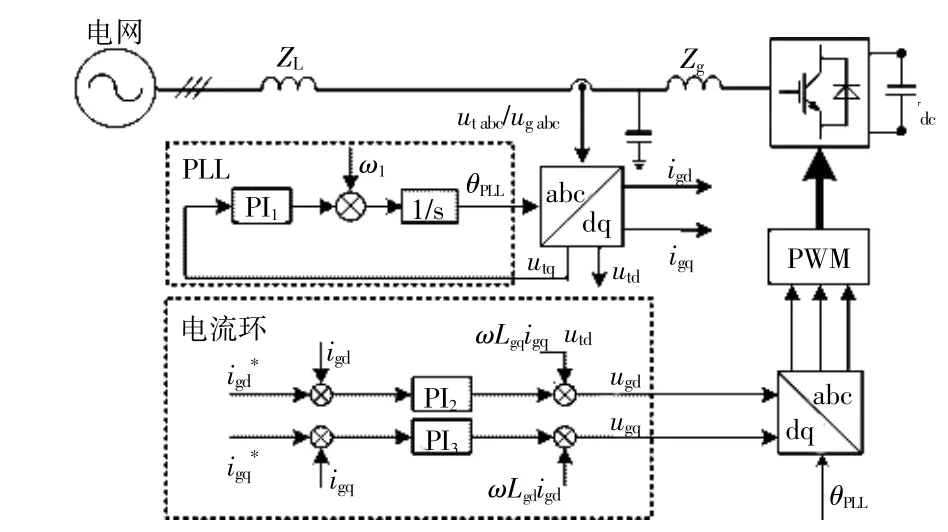
图1 并网逆变器系统的控制框图Fig.1 The diagram of the grid-connected inverter system

由图1可知，PLL将两相旋转dq坐标的d轴定向到电网电压矢量上，为整个系统提供准确的电网电压相位同步信息[2]。由于相位同步检测是实现矢量控制的基础，且并网逆变器控制系统的坐标变换、有功、无功功率的调制均以PLL输出的相角信息为准，因此PLL的动态特性将直接影响控制系统的整体性能。

根据图1可得典型PLL控制器的小信号模型为

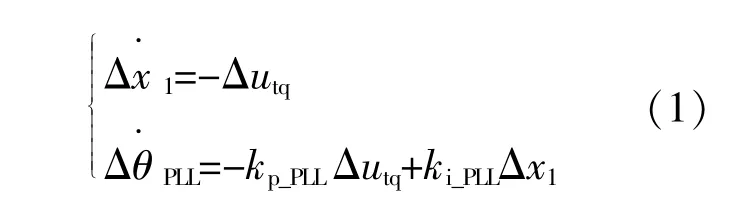
式中:kp_PLL，ki_PLL分别为PLL的PI控制器比例和积分系数；x1为引入PLL的PI控制器对应的状态变量；ΔθPLL为输出相角的增量。

PLL输出角频率的增量ΔωPLL为

式中:kp_cc，ki_cc分别为电流环的PI控制器比例和积分系数；x2，x3为引入电流环PI控制器对应的状态变量。

由式（3）可得并网逆变器系统电流环的小信号模型线性化方程:

由式（4）可知，逆变器输出电流ig的动态不仅受系统端电压ut的影响，同时也受PLL动态的影响。

根据基尔霍夫定律，系统端电压ut可通过电网电压uG与线路阻抗压降uL表示，即:

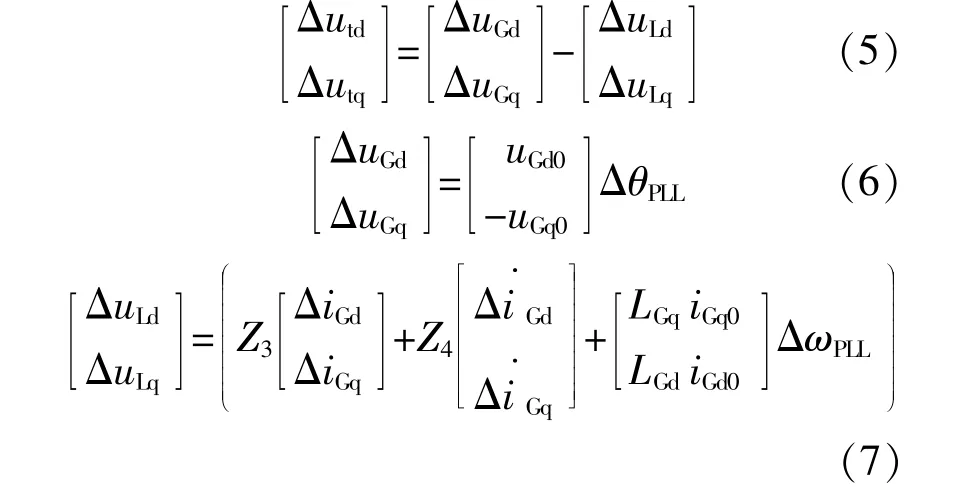
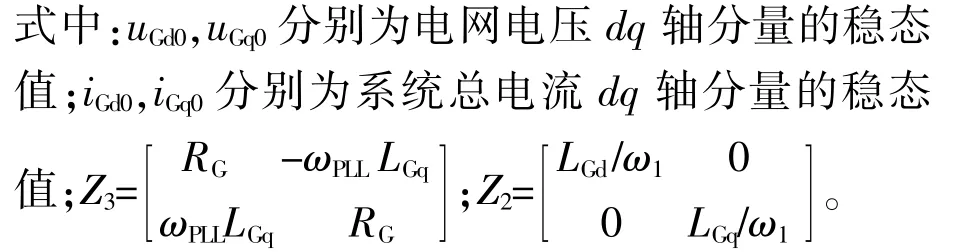
由式（7）可知，电网阻抗压降uL与线路阻抗成正比，当线路阻抗越大时，uL对端电压ut影响越大，也将加大对PLL动态特性的影响。此外，由于逆变器出口端处常设有LC型滤波器以防止高次谐波电流流入电网，因此，根据基尔霍夫电流定律，系统总电流iG的增量为

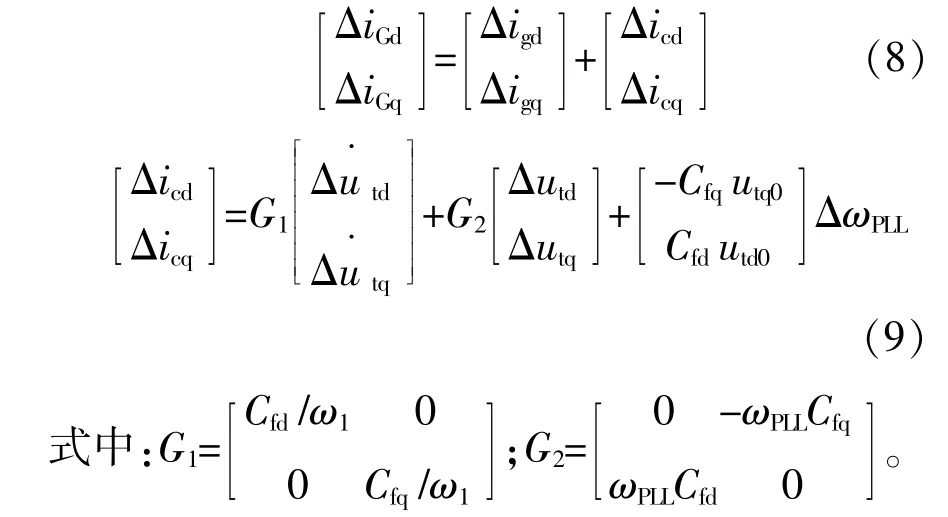
分别将式（4），（6）～（9）代入式（5）进行化简，可推导出端电压矢量ut在PLL同步旋转坐标系中的小信号状态方程为

由式（10）可以看出，逆变器输出电流ig的动态会对端电压ut产生影响，并进一步影响PLL的动态。另外，根据Z5的表达式可知，电网阻抗越大，ig对PLL动态行为影响越大。结合式（4）可知，PLL与电流环之间存在相互作用，并且随线路阻抗增大而加剧。因此，在弱电网条件下，PLL与电流环之间的交互影响作用可能引发系统的小信号失稳。

2 并网逆变器系统在LVRT期间的特征值分析

本文基于Matlab/Simulink建立图1的并网逆变器系统时域仿真模型，并采用基于状态空间方程的特征值分析法，以分析并网逆变器系统在LVRT期间的小干扰运行特性，系统参数如表1所示。

表1 并网逆变器系统参数Table 1 Parameters of grid-connected inverter system

续表1

结合表1及仿真模型所得系统参数，可获取并网逆变器系统状态矩阵所需的全部稳态运行点初始值。并结合前文建立的小信号模型以及系统中各变量之间的耦合关系，选取系统状态变量Δx=[Δx1，Δx2，Δx3，ΔθPLL，ΔiGd，ΔiGq，Δutd，Δutq，Δigd，Δigq]T，建立全系统的小信号线性化状态空间方程为

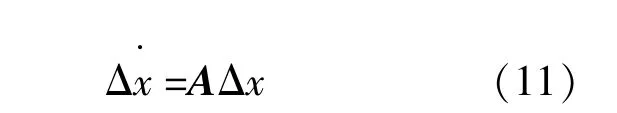
式中:A为状态矩阵，其特征值可以反映系统的小信号稳定性矩阵。

通过求解式（11），可以得到系统的所有振荡模态及其相应的参与因子，进而可以分析得出导致并网逆变器系统在LVRT期间出现小信号不稳定性的主要因素。

当电网电压跌落至额定值的20%时，系统特征值计算结果如表2所示。

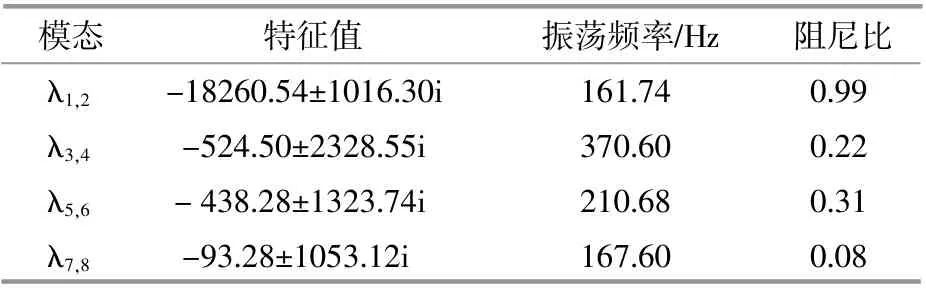
表2 特征值分析结果Table 2 Eigenvalue analysis results

根据表2可以得出，系统共存在4对共轭复数特征值，表明系统共存在4个周期性振荡模态。其中，振荡模态λ7，8的阻尼比最小，意味着其抗扰动能力最弱，即当外界条件或系统参数变化时，很可能导致振荡模态λ7，8特征值实部由负变正，这表示系统将趋向于不稳定。由此可见，该并网逆变器系统存在潜在的小信号失稳风险。

为分析系统各振荡模态的特性，以电网电压跌落至20%，线路阻抗0.5 p.u.为例，计算各状态变量关于各个振荡模态的参与因子，计算结果如表3所示。 由表3可以看出，振荡模态λ7，8与PLL对应的状态变量Δx1和ΔθPLL关系密切，因而PLL对并网逆变器系统的稳定性有着显著影响。

表3 状态变量关于振荡模态的主要参与因子Table 3 Major participation factors of state variables in modes

3 系统参数对并网逆变器系统小干扰稳定的影响规律分析

根据特征值分析结果可知，振荡模态λ7，8的阻尼比较弱，极易因外界条件及系统参数的变化而变为负阻尼振荡模态，此时系统将趋于失稳并振荡发散。此外，通过表3各振荡模态中不同状态变量的参与因子分布情况可得，该弱阻尼振荡模态λ7，8主要与PLL相关。考虑到弱电网下PLL与电流环、线路阻抗之间相互影响会进一步影响系统的稳定性，因此，将分别分析电网强度、PLL参数及电流环参数对系统在低电压穿越期间各振荡模态的影响规律。

3.1 电网强度对系统小干扰稳定的影响

根据前文分析可以看出，电网线路阻抗会对端电压ut的动态产生影响，并进而影响PLL的动态行为。随着线路阻抗的增大，其对锁相环动态的影响也会增加，PLL与电流控制之间的相互作用也会增强。在模态分析中，通过改变线路阻抗来改变短路比（Short Circuit Ratio，SCR），进而改变电网强度，当SCR从3.0逐渐减小至1.2时，系统各振荡模态的特征值变化轨迹，如图2所示。由于λ3，4，λ5，6和λ7，8对应特征根分布比较密集，对特征根进行了局部放大，箭头方向表示电网强度减弱的方向。

图2 不同电网强度下的根轨迹Fig.2 The eigenvalues locus with different grid strengths

由图2可知，当电网强度减弱时，振荡模态λ1，2、λ3，4和λ5，6对应的特征值变化较大。其中，λ1，2和λ5，6逐渐向右移动，而λ3，4向左移动，但三者的特征根实部始终为较大负值。因此并网逆变器系统并不会受电网强度影响而诱发此类振荡；只有振荡模态λ7，8对应的特征根会因电网强度减弱而逐渐右移趋向虚轴。当SCR＜1.8时进入右半平面，如图中加号所示，此时并网逆变器系统不稳定。由此可得在弱连接电网条件下系统存在振荡风险，其对应振荡模态为λ7，8，且电网强度越弱，系统稳定性越差。

3.2 锁相环带宽对系统小干扰稳定的影响

图3显示了PLL带宽由10.2 Hz增加到16.6 Hz时，系统各振荡模态对应特征值的变化轨迹。由图3可得，当PLL带宽增加时，只有振荡模态λ7，8对应特征值将从左半平面穿越虚轴进入右半平面不稳定区域，而其他系统振荡模态的特征值均不会因PLL带宽的改变而有较大变化，且始终位于虚轴左侧稳定区域内。因此，由于振荡模态λ7，8的缘故，PLL带宽的增加将不利于系统稳定性。

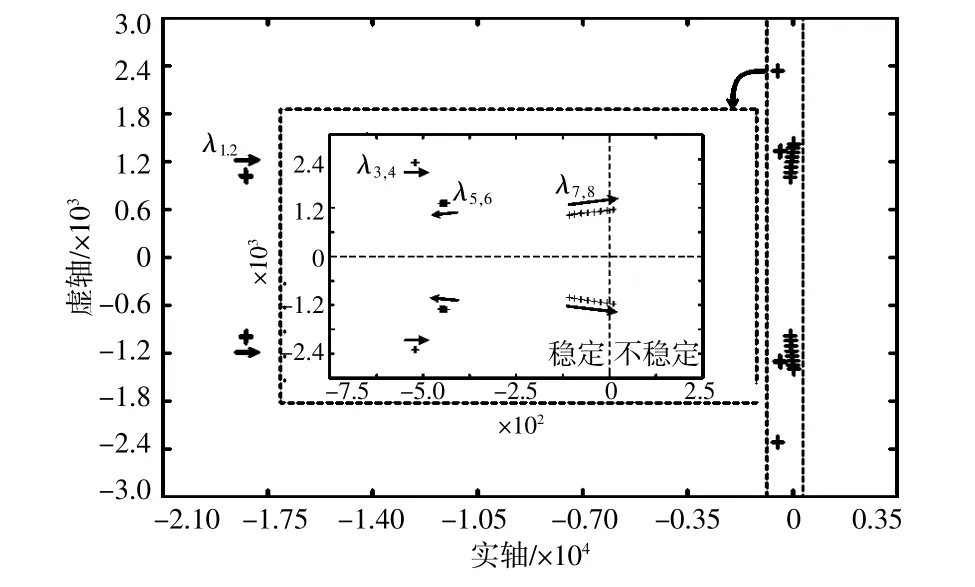
图3 不同锁相环带宽下的根轨迹Fig.3 The eigenvalues locus with different PLL's bandwidth

3.3 电流环带宽对系统小干扰稳定的影响

逆变器系统电流控制环带宽从112.5 Hz增大到262.3 Hz时，系统各个振荡模态的根轨迹如图4所示。由图4可知，当电流控制环带宽增加时，与网侧电流强相关的振荡模态λ1，2趋向右移，但其特征值始终具有较大负实部。振荡模态λ3，4和λ5，6变化不大，只有振荡模态λ7，8对应特征值会随着电流环带宽的增加而逐渐右移，并在电流控制环带宽超过262.3 Hz后穿越虚轴进入右半平面，此时系统不稳定。因此，电流环带宽的增大将会削弱该系统稳定性，甚至导致其失稳。

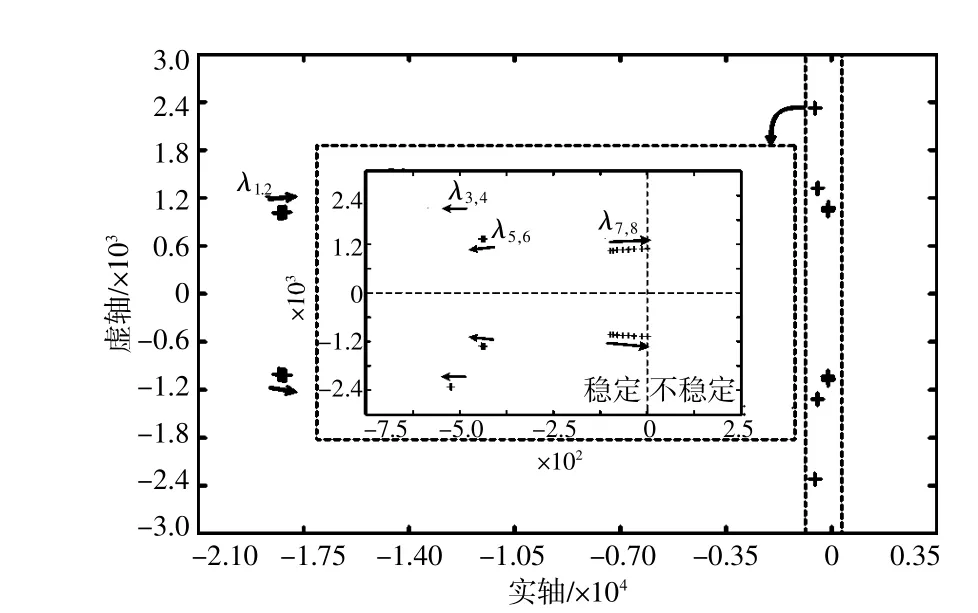
图4 不同电流环带宽下的根轨迹Fig.4 The eigenvalues locus with different current controller's bandwidth

通过以上对系统稳定性影响因素的分析得出，在低电压穿越过程中，电网强度越弱、锁相环和电流控制器响应越快，都可能导致系统更容易出现小信号失稳。因此，适当调整PLL和电流控制器的带宽等参数，对于弱电网下并网逆变器系统在低电压穿越期间的稳定性是非常重要的。

4 仿真验证

为验证上述特征值分析结果的正确性，利用Matlab/Simulink所搭建的并网逆变器系统详细模型进行时域仿真验证。仿真期间，t=4 s时系统发生三相对称短路故障，t=5 s时故障切除。

4.1 不同电网强度下的时域仿真结果

设置电压跌落至20%额定电压，且PLL和电流环带宽分别为13.4 Hz和187.4 Hz时，研究SCR分别为2，3时系统的小信号稳定性。时域仿真波形分别如图5所示。

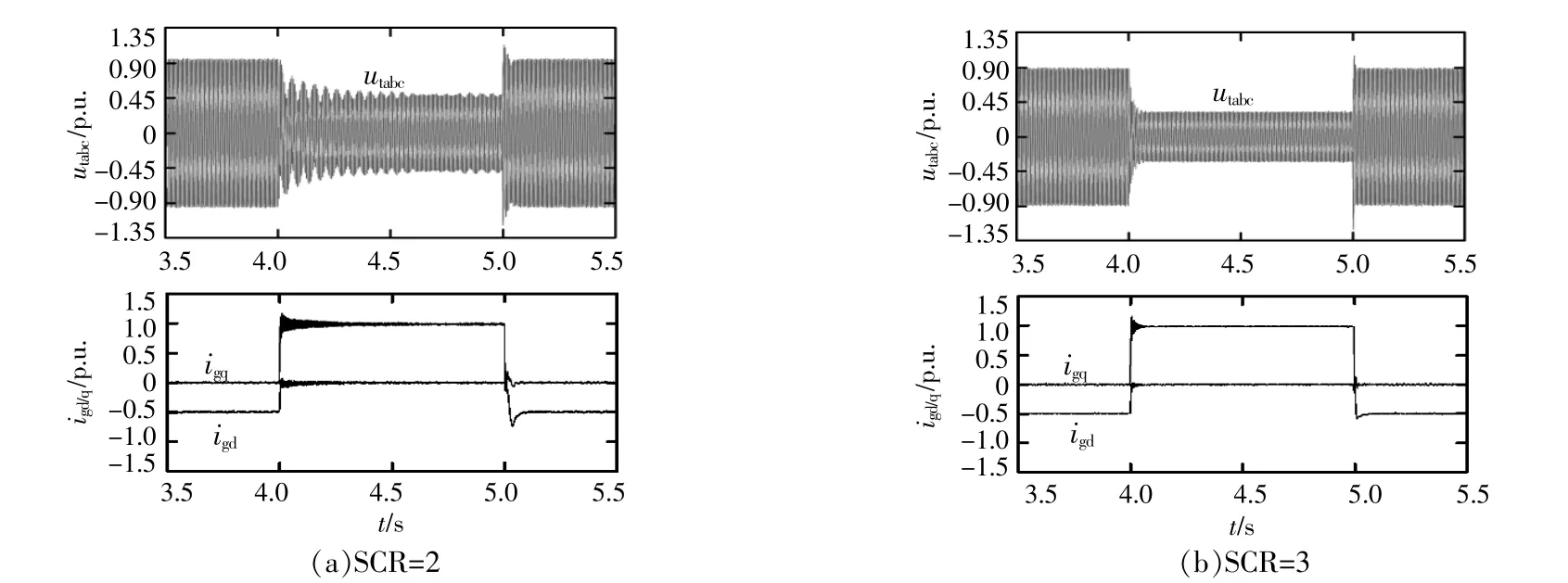
图5 不同电网强度下的电压与电流仿真波形Fig.5 The waveform of voltage and current with different grid strength

由图5可知，当SCR=2时，故障期间系统存在收敛速度较慢的小干扰振荡现象；当SCR增大时，该振荡的衰减速度增加，系统达到低电压穿越期间稳定运行点的时间减少。由此电网强度越弱，低电压穿越期间系统越易产生小干扰振荡，这与前文理论分析结果一致。

4.2 不同PLL带宽下的时域仿真结果

当SCR为2，电网电压跌落至20%时，通过降低PLL比例系数来减小其带宽。图6为当PLL带宽为15.1Hz和11.7Hz时的时域仿真波形。

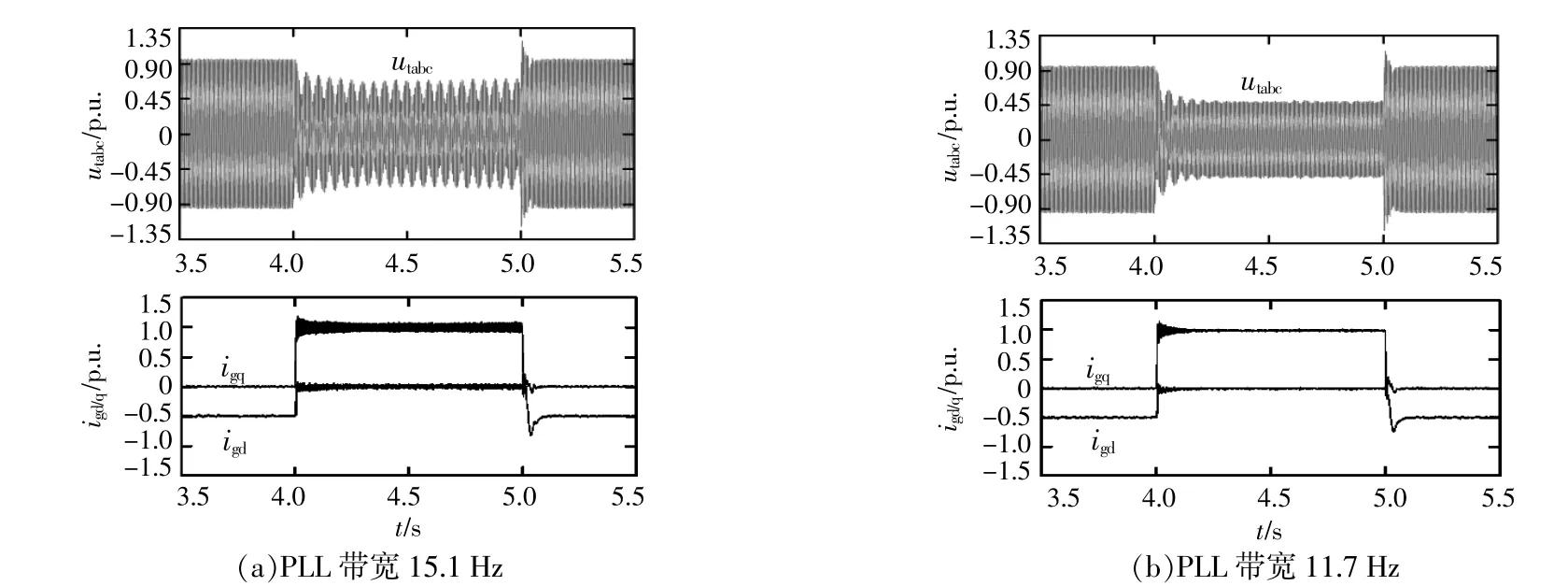
图6 不同锁相环带宽下的电压与电流仿真波形Fig.6 The waveform of voltage and current with different PLL's bandwidths

由图6可知，当锁相环带宽为15.1 Hz时，低电压穿越期间系统出现等幅的小干扰振荡现象，减小带宽至11.7 Hz时，系统小干扰振荡能够快速收敛。通过对比可知，减小PLL带宽，可以提高低电压穿越期间系统小干扰稳定性。该结论与前文理论分析结果一致。

4.3 不同电流环带宽下的时域仿真结果

当SCR=2，电网电压跌落至20%时，电流控制环带宽等于262.3 Hz和135.0 Hz时仿真结果如图7所示。

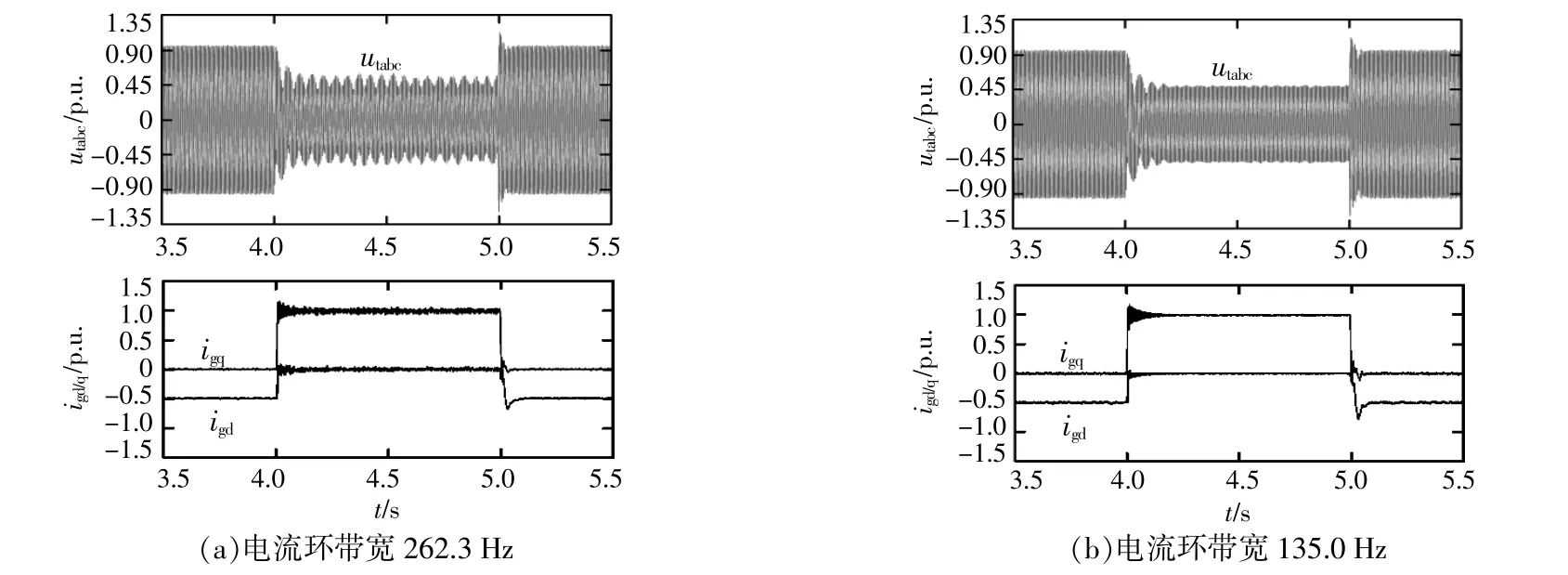
图7 不同电流环带宽下的电压与电流仿真波形Fig.7 The waveform of voltage and current with different bandwidths of the current controller

由仿真结果可知，电流控制环带宽越大，低电压穿越期间系统小干扰振荡越剧烈，系统稳定性越弱。由此可以得出，减小电流环带宽，将有助于提高低电压穿越期间系统小干扰稳定性。该仿真结果也验证了前文理论分析的正确性。

5 结论

本文对并网逆变器在LVRT期间的小干扰稳定性展开详细研究，通过全面考虑PLL，电流环以及电网阻抗的影响，建立了适用于小干扰振荡分析的并网逆变器系统详细数学模型，推导出电网阻抗、锁相环及网侧电流环之间的耦合作用关系。分析结果表明，电流环的响应会受PLL的动态所影响，同时电流动态通过线路方程将传递到端电压，从而又会影响到PLL的动态行为，由此可知电网阻抗、PLL及电流环经由端电压相互耦合，进而影响系统在低电压穿越期间的小干扰稳定性。

本文基于所建模型，采用特征值分析法对并网逆变器系统进行了全面的模态分析，得到了系统各振荡模态的特性，并进一步确定出具有最弱阻尼的振荡模态。在此基础上，通过系统根轨迹图详细分析了电网阻抗、锁相环带宽及电流环带宽对系统小干扰振荡特性的影响规律，并通过时域仿真对模态分析结果的正确性进行了验证。分析结果表明，电网强度减弱将导致系统在低电压穿越期间的小干扰稳定性减弱，而锁相环带宽及电流环带宽的减小则有利于提高系统的小干扰稳定性。该规律可用于指导LVRT期间并网逆变器控制参数的选取，从而提高并网逆变器LVRT期间的小干扰稳定性。