具有角速度和输入约束的航天器姿态协同控制

郑重 李鹏 钱默抒

在航天器编队飞行任务中,航天器系统依照特定的任务要求,通过信息交互协作完成共同目标,形成一个分布式空间系统,从而完成传统的单一大型航天器难以实现的复杂空间任务.由于航天器编队系统具有鲁棒性强、可靠性高、发射成本低等优点,成为近年来研究的热点[1].为了保证航天器编队系统能够完全实现特定的空间任务,需要利用航天器之间的相对信息进行协同控制.

姿态协同控制是航天器编队在轨运行的一项重要的关键技术,目前国内外学者已对其进行了较多研究[2−12],取得了一定的研究成果.然而,这些结果大多是采用四元数或罗德里格参数表示姿态,由于四元数表示姿态具有非唯一性,可能导致出现姿态展开现象[13],因此航天器在跟踪外界姿态信号时,航天器相对姿态的一致性很难得到保持.对于采用罗德里格参数描述的姿态控制设计方法,同样存在姿态展开问题[14].解决姿态展开问题一般有两种方法,一种是采用四元数和修正罗德里格参数(Modified Rodrigues parameters,MRP)的切换系统混杂控制实现全局姿态跟踪[15],但是这种控制算法是非连续的,很难直接应用于飞轮、磁力矩器、控制力矩陀螺等提供连续的控制信号的航天器执行机构中;第二种是直接基于旋转矩阵描述姿态运动并设计协同控制器.因为旋转矩阵在描述姿态运动时是无奇异的,并且它与航天器姿态是一一对应的关系,所以基于旋转矩阵描述姿态,并设计姿态协同控制算法能够有效避免上述姿态展开现象.文献[16] 采用旋转矩阵描述的姿态运动数学模型,在只需要相对姿态误差的情况下设计了自主姿态协同控制方法.文献[17] 利用系统无源控制方法提出了角速度控制律并证明了姿态的一致性,但是没有考虑系统姿态动力学方程.文献[18] 在仅利用了相对姿态误差情况下给出了角速度控制策略,同时进一步分析了发生通信拓扑切换情况的系统稳定性.文献[19] 给出了基于旋转矩阵的姿态运动学方程,在没有参考信息情况下设计了姿态同步控制算法,并且分析了控制算法对于常值通信时滞的鲁棒性.文献[20] 采用旋转矩阵描述航天器姿态,在有向通信图下设计了姿态协同控制算法,并且同时研究了通信时滞、外界扰动和模型不确定性的影响.

在航天器姿态控制过程中,往往需要角速度和控制输入满足一定的约束.如在XTE (X-ray timing explorer,X 射线定时探测器)航天器姿态机动过程中,角速度陀螺需要满足幅值受限的要求[21],因此角速度最大值不能超过给定的范围.同时,飞轮、磁力矩器等执行机构只能提供有限的控制力矩,如果控制指令给出的控制力矩太大,则控制系统可能发生控制输入受限问题,导致控制性能下降,甚至是整个编队系统的失稳.针对此问题,Hu 等[22]采用非线性PD 控制使得航天器跟踪期望的姿态,满足角速度有界的要求,同时考虑了执行器不确定性.进一步,Hu 等在文献[23] 中考虑了执行器的死区非线性和姿态展开,在文献[24] 中研究了角速度和输入幅值受限情况下姿态跟踪控制问题.Shen 等[25]采用势函数方法设计了自适应姿态跟踪控制器,保证姿态角和角速度都能够在跟定的范围内变化.Yu等[26]采用滑模控制设计姿态跟踪控制算法,能够实现角速度和控制输入在给定的界内.然而,在采用旋转矩阵的姿态协同控制中,目前还几乎没有学者同时考虑角速度和控制输入受限问题,特别是航天器还受到外界扰动和通信时滞的影响等情况.

本文主要采用旋转矩阵描述的姿态跟踪控制动力学模型,在有向通信结构下设计了能够同时保证角速度和控制输入有界的鲁棒姿态协同控制算法.本文创新点包括:1)对于采用旋转矩阵的闭环系统多个平衡点问题,给出了详细的稳定性分析,并证明了系统的几乎全局渐近稳定性;2)采用新的势函数方法设计具有角速度限制的控制器,并且设计了新的滤波器补偿控制输入受限;3)考虑了可能存在信息传输时滞的情况,设计了对通信时滞具有鲁棒性的姿态协同控制算法.

1 相关理论基础

1.1 航天器姿态动力学模型

本文考虑n个航天器组成航天器编队系统,采用旋转矩阵描述航天器姿态运动.假设航天器存在输入饱和约束,则第i个航天器姿态运动学和动力学方程为[20]

式中:Ji∈R3×3表示航天器的转动惯量矩阵;ωi∈R3为体坐标系表示下的角速度;ui,di∈R3分别表示控制力矩和扰动力矩,扰动的界可表示为‖di‖∞≤d0,d0>0 为未知常数;令ui=sat(τi),sat 为饱和函数,即对于向量y=[y1y2y3]T,

sgn(·)为符号函数,τ0>0 为控制输入的上界.Ri∈SO(3)表示本体坐标系到惯性坐标系的旋转矩阵;表示向量ωi=[ω1ω2ω3]T对应的反对称阵,即

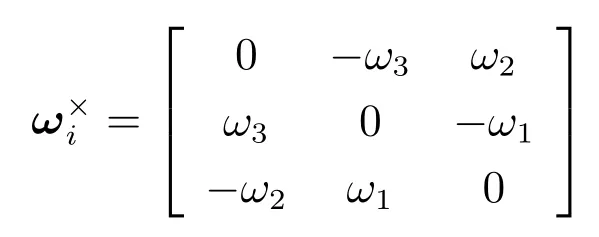
上述叉乘运算把三维向量映射为反对称矩阵,设其逆运算为∨,则可得[20]

其中φ(A)=(A−AT)∨,x∈R3,A∈R3×3,R∈SO(3).

记期望的姿态为Rd∈SO(3),期望的角速度为ωd∈R3,并且满足

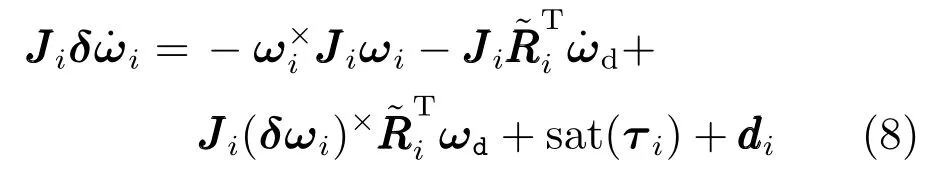
本文的目的即为,设计控制器使得航天器在满足角速度和控制约束下,实现协同一致地跟踪期望的姿态,即

并且当t→∞时,Ri→Rd,ωi→ωd.

1.2 图论

图是由若干给定的节点和连接两个节点的边集所构成的,记为G=(υ,ς,C),它由节点集υ={υ1,υ2,···,υn}、边集ς ⊆υ×υ和加权邻接矩阵C=[cij]∈Rn×n组成[27].如果节点υi能直接得到节点υj的信息,则图中就包含一条从υj指向υi的边,记为(υi,υj)∈ς.加权邻接矩阵C中的元素定义为:当(υi,υj)∈ς时,cij >0;否则,cij=0.无向图中要求cij=cji,即C是主对角元素为零的对称矩阵;而有向图中C则不一定是对称的.如果对于i=1,2,···,n,有成立,则称图G是平衡的.

2 控制器设计

2.1 姿态协同控制器设计

定义姿态跟踪误差为

其中tr 表示矩阵的迹,显然有0≤ei≤4 成立.由式(4)和式(7),ei的导数可计算为

利用式(3)～(5),的导数可进一步计算为

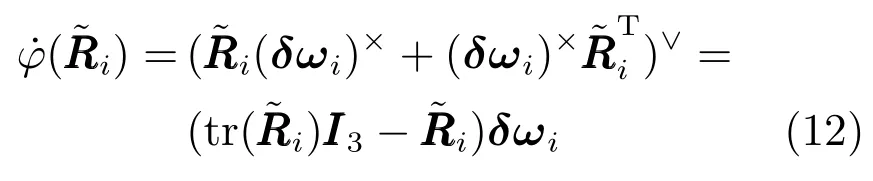
定义总误差变量为

式中常数αi >0.在控制器设计之前首先给出下面引理1.

引理1.如果si∈L2且,则当t→∞时,.

证明.由式(11)可得

其中T >0.由式(13)且si∈L2,可得

因此δωi∈L2和成立.此外,由于si∈L∞,,可得δωi∈L∞,因此由式(12)可得,由可得∈L∞.因此由Barbalat 引理[28]可得,当t→∞时,δωi→0 且成立.

定义1.考虑如下非线性动态系统

其中U为状态空间集合,并且系统存在某个平衡点xe.如果系统是Lyapunov 稳定的,并且存在一个零测度集U0,对于与任意的x0∈UU0,成立

则称平衡点xe是几乎全局渐近稳定的.

为了补偿控制输入饱和的影响,设计滤波器ξi为

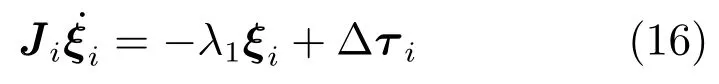
式中常数λ1>0,Δτi=sat(τi)−τi表示输入饱和约束下的有界控制与所设计的控制之差.因此由式(8)可得

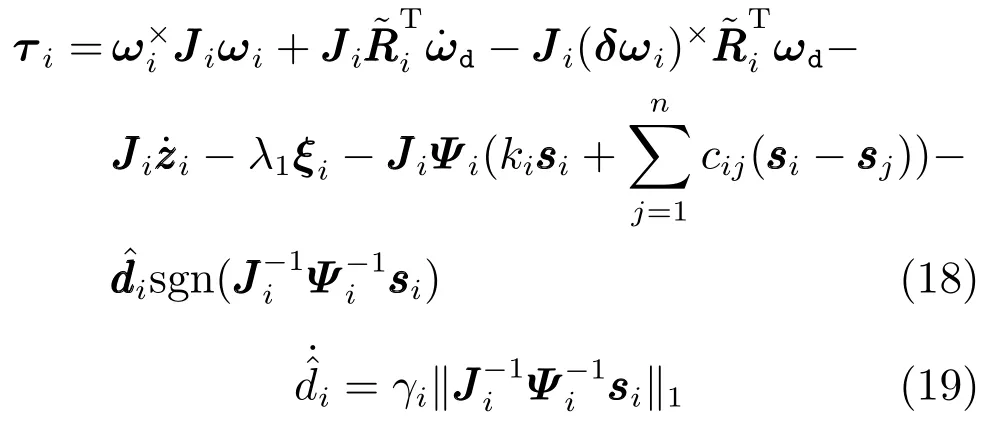
式中:cij表示加权邻接矩阵C中的元素;为扰动上界d0的估计值,且要求;常数γi >0;矩阵Ψi为

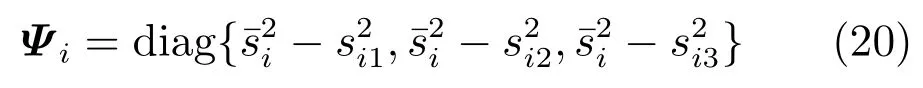
式中si=[si1si2si3]T,为si的上界,并且本文假设系统初值满足,k=1,2,3.

定理1.对于航天器姿态控制系统(1)和(2),定义集合,在滤波器式(16)、控制器式(18)和自适应律式(19)作用下,如果航天器之间的通信拓扑图为平衡有向图,则可得:

1)集合Pi中的任意一点都是不稳定的平衡点;

2)闭环系统具有几乎全局渐近稳定性,即对于除了一个测度为零的集合之外的系统初始状态,系统轨迹收敛到集合中,当t→∞时,Ri→Rd,δωi→0;

3)对于任意时刻,航天器角速度和控制输入满足约束‖ωi‖∞≤ω0,‖ui‖∞≤τ0.

证明.选取Lyapunov 函数为

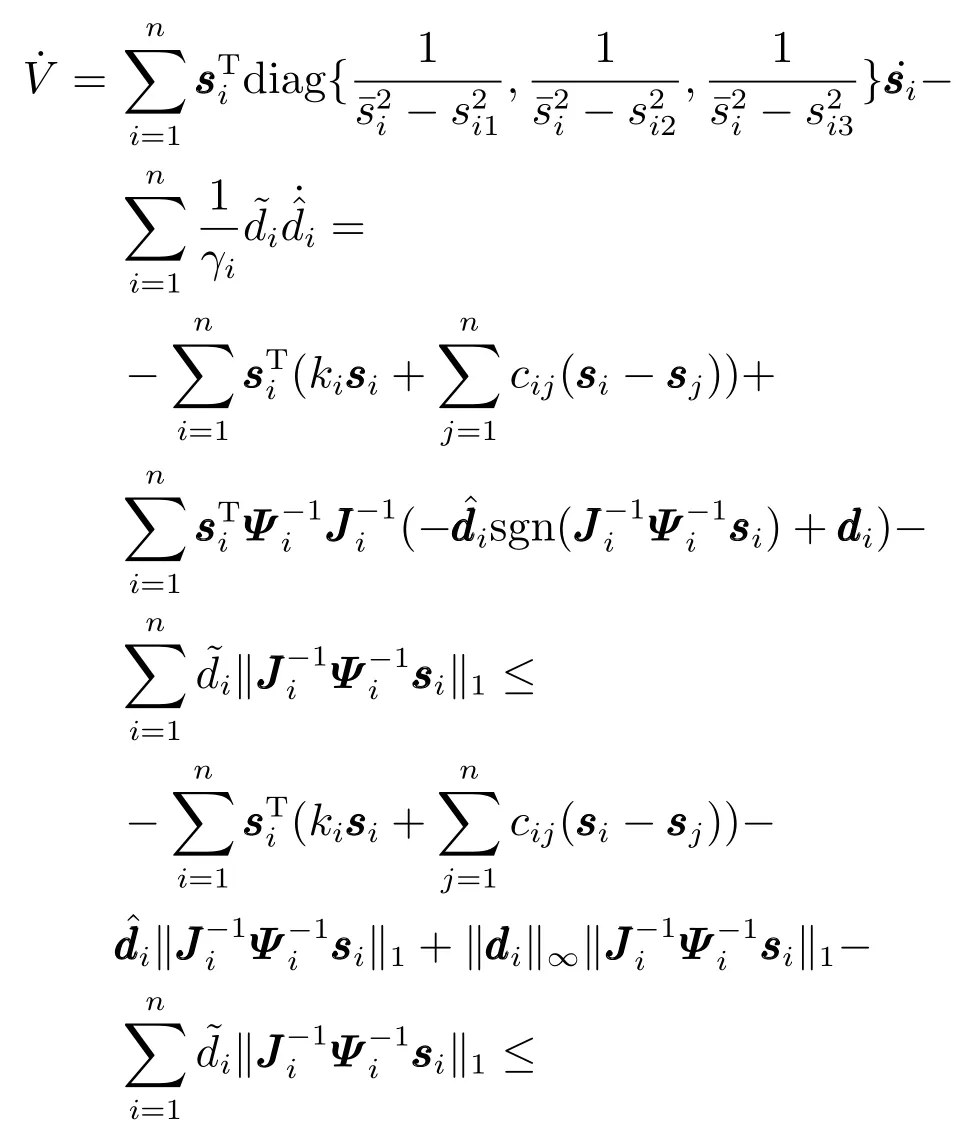
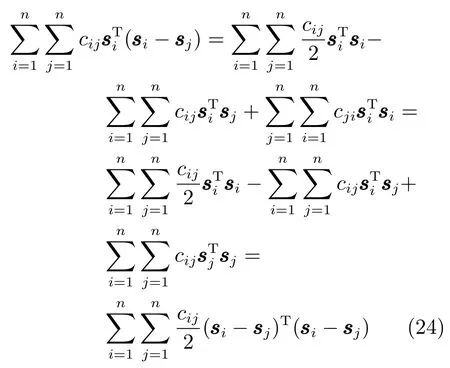
把式(24)代入式(23)可得

因此V有界,并由式(22)可知si,∈L∞,对式(25)两边积分可得

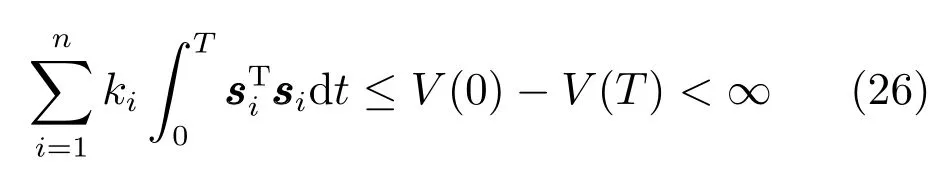
因此si∈L2,由引理1 可得当t→∞时,δωi→0,.系统的平衡点为

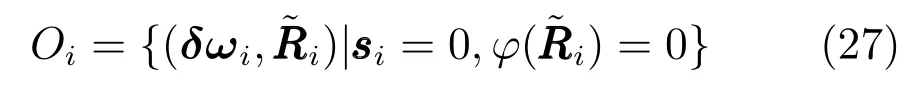
下面利用旋转矩阵的四元数表示证明结论1).设qd为Rd对应的期望四元数,qi表示Ri对应的四元数,误差四元数定义为,其中表示四元数qd的共轭,°表示四元数乘法.对于四元数,相应的旋转矩阵为,从而在集合Oi中,有=4qi1qiv=0,因此qi1=0 或者qiv=0.可得Pi==0,qi1=0},此时qi1的动力学方程可表示为

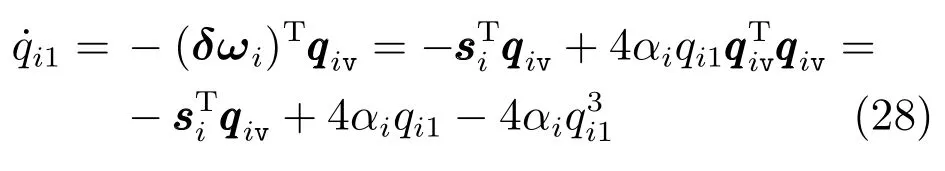
由于αi >0,因此平衡点qi1=0 是不稳定的,并且si收敛到0,所以集合Pi中的任意点都是不稳定的平衡点.由此证明了结论1).

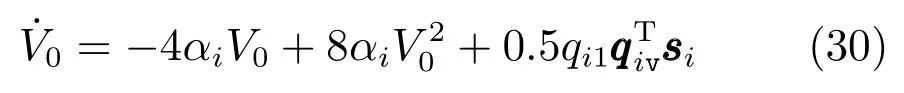
由si→0 和αi >0,可得V0→0,因此qiv→0.由此可得集合Qi中任意点都是稳定的平衡点.

同时,系统轨迹可能沿着变量si的稳定中心流形逐渐收敛到集合Pi中.由文献[29] 的结果可知,这些系统轨迹集合在整个状态空间的测度为0,而且不稳定的平衡点集合Pi在状态空间R3×SO(3)上的测度也为0,这就证明了,如果初始状态不在这个零测度集,则系统轨迹收敛到期望的平衡点中,即当t→∞时,Ri→Rd,δωi→0.由此证明了结论2).

当|sik|<时,有界,并且当|sik|→时,→∞,由于V有界,可知|sik(t)|<,所以是存在的并且不会出现奇异,并且

因此

并且

由此证明了结论3). □

2.2 通信时滞下的姿态协同控制器设计

为了实现姿态的协同控制,航天器需要获取相对姿态信息,这些信息可以通过无线传输等通信方式得到.由于航天器通信距离较远和信息传输设备的物理限制,信息传输过程中可能产生通信时滞.本节进一步研究航天器编队系统中存在通信时滞的情况,则航天器只能得到时滞发生后的信息sj(t−Tij),此时控制器为

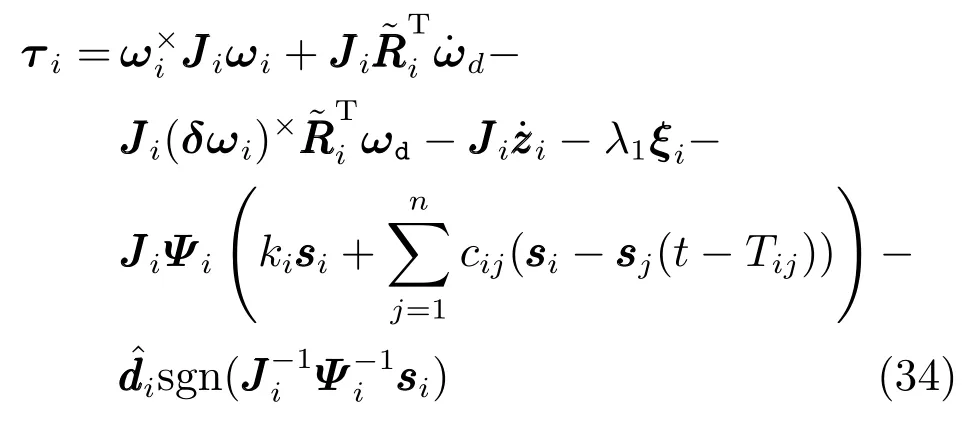
其中Tij(t)≥0 是时变的.假设时滞量Tij的精确值未知,但是的上界是已知的,并且满足≤hij <1.则可以得到下面的定理2.

定理2.对于航天器姿态控制系统(1)和(2),定义集合,在控制器式(16)、式(34)和式(19)的作用下,如果航天器的通信拓扑图为平衡有向图,且控制器参数满足

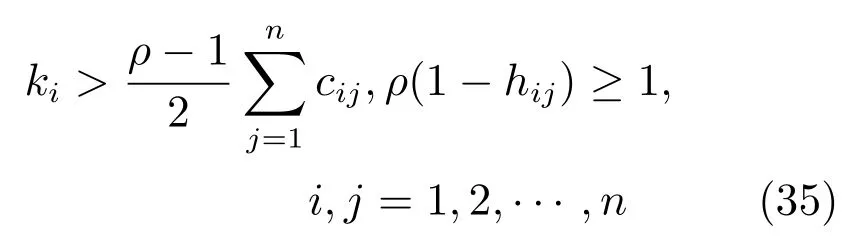
式中常数ρ>1.则定理1 中的结论仍然成立.

证明.选取Lyapunov 函数为

对上式求导可得

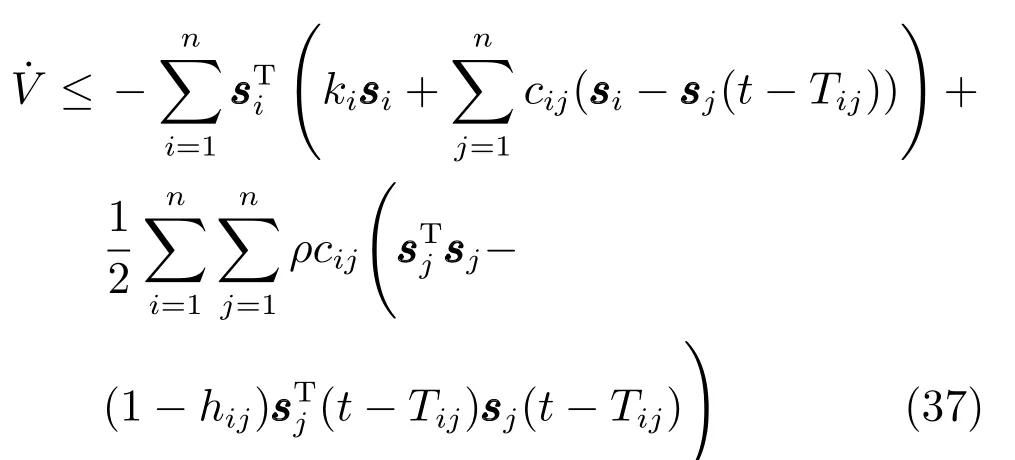
注意到

把式(38)和式(39)代入式(37)可得

因此si∈L2,由引理1 可得当t→∞时,δωi→0,→0.接下来的证明与定理1 的证明过程类似,同样可以得到定理1 中的3 条结论,在此不再赘述. □

3 数值仿真

本节采用MATLAB 进行数值仿真以验证所提出控制算法的有效性,为了简便考虑,只对具有通信时滞的控制器(34)进行验证.假设四个航天器组成编队系统,航天器受到的扰动为

航天器的转动惯量矩阵设为

航天器的初始角速度设为0,初始姿态设为

期望角速度取为

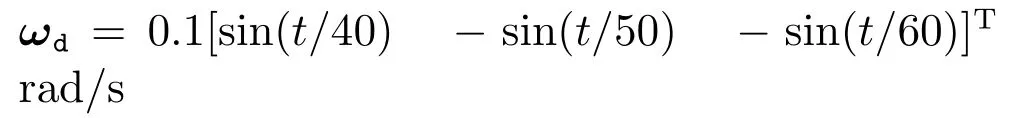
期望旋转矩阵的初始值取为

控制器(34)的加权邻接矩阵C选取为

控制器(34)的参数选取为αi=0.1,ki=15,λ1=0.2,自适应律式(16)和式(19)参数分别选取为ξi(0)=[0.1 0.1 0.1]T,=0.001 N·m,γi=0.00005.时变的通信时滞取为

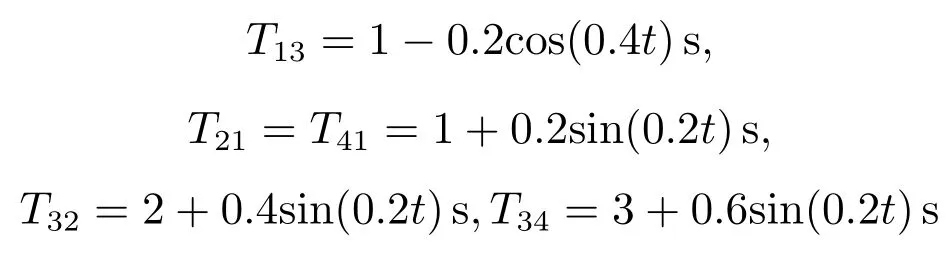
要求的角速度和控制输入上界分别取为

令常数ρ=3,则显然在所选取的控制器参数下,式(35)能够得到满足.

定义航天器的姿态角误差σi为

显然当σi=0 时,Ri=Rd,表明实现了航天器的姿态同步跟踪.控制器(34)的仿真结果如图1～5所示.图1 给出了航天器的姿态误差角的变化曲线,可以看出姿态误差角最终收敛到零,表明航天器姿态最终收敛到期望的姿态.图2 给出了航天器角速度误差的曲线,航天器角速度跟踪误差也能收敛到零.图3 和图4 给出了航天器角速度和控制力拒的变化曲线,可以看出角速度和控制力矩都能够满足事先所给定的有界性约束.图5 给出了滤波器ξi的曲线,从图中可以看出ξi最终收敛到0.

图1 控制器(34)下的姿态角误差Fig.1 Attitude angle error with controller (34)

图2 控制器(34)下的角速度误差Fig.2 Angular velocity error with controller (34)

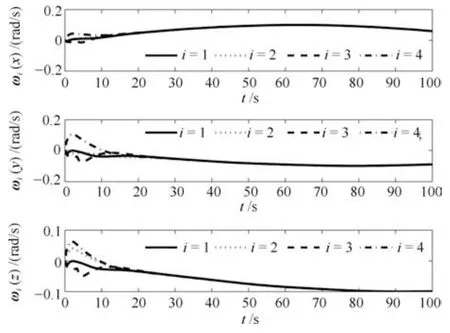
图3 控制器(34)下的角速度Fig.3 Angular velocity with controller (34)

图4 控制器(34)下的控制力拒Fig.4 Control torque with controller (34)

图5 控制器(34)下的滤波器ξiFig.5 The filter ξi with controller (34)

为了进一步研究本文提出控制方法的性能,把控制器(34)和如下未考虑角速度和输入约束的控制器作对比

控制器(42)的仿真结果如图6～8 所示.图6 给出了控制器(42)下的姿态误差角的变化曲线,对比图1 和图6 可以看出,两种控制器下姿态误差角都在大约30 s 收敛到零附近.图7 给出了控制器(42)下的角速度,从图中可以看出角速度y轴分量已经超过角速度上界ω0=0.5 rad/s,说明控制器(42)无法满足角速度约束.图8 为控制器(42)下的控制力矩,同样从图中可以看出控制力矩y轴分量超过控制输入上界τ0=5 N·m,控制器(42)也无法满足控制输入约束.因此,提出的控制器(34)与常规控制器(42)具有相当的控制性能,并且满足角速度和输入约束.

图6 控制器(42)下的姿态角误差Fig.6 Attitude angle error with controller (42)

图7 控控制器(42)下的角速度Fig.7 Angular velocity with controller (42)

图8 控制器(42)下的控制力拒Fig.8 Control torque with controller (42)

4 结论

在通信图是有向的情况下,设计了基于旋转矩阵描述的自适应鲁棒姿态协同控制算法,保证了系统角速度和控制输入满足有界性的约束,并分析了系统的Lyapunov 稳定性,证明了闭环系统在期望的平衡点具有几乎全局渐近稳定性.当外界扰动存在时,提出了自适应算法估计外界扰动的上界,并且设计滤波器补偿控制输入饱和的影响,对于所设计的控制算法,通过稳定性分析,证明了对于除了一个测度为零的集合之外的系统初始状态,系统误差能够收敛到0;进一步把结果推广到时变通信时滞情况,仍然能够保证系统具有几乎全局渐近稳定性,以及对通信时滞的鲁棒性.仿真结果进一步表明系统在所设计的控制算法下具有较好的性能.