嵌套删失数据期望最大化的高斯混合聚类算法
2021-07-25余海燕陈京京王若凡
余海燕 陈京京 邱 航 , 王 永 王若凡
高斯混合聚类[1−2]作为统计机器学习、模式识别和阵列数据分析等的重要模型,广泛用于健康医疗[3−4]、故障诊断[5−6]等领域.然而,常因诸如截断的数据、传感器故障或传输错误等造成数据不完整问题[1],引起推断偏差并使得聚类精度下降.例如在医疗决策智能支持中[7−8],需要依据患者的各项生理指标信息进行智能推理[9−10],然而由于记录数据删失或截断等导致数据不完整,从而给数据分析带来困难.在恶性淋巴瘤等疾病诊断[11]中,流式细胞仪记录的数据因测量信号强度范围有限而使得数据记录在一个固定范围内(如0 到1 023 之间),如果测量值超出这一范围,则该值将替换为最接近的值,小于0的值将被删失记为0,大于1 023 的值将被删失记为1023.类似的删失数据还包括保险费理赔计算中,因一定数量免赔额的存在使得记录成为删失数据等.这类删失数据处理不当会影响分析结果的可靠性,甚至使得聚类模型参数推断出现较大偏差.又因这类数据的分布参数的精确估计,为处理变量或治疗方案对观察结果的因果效应分析[12]提供基础,甚至影响到后续的决策方案选择.高斯聚类算法因能够提供分布参数的估计,故而删失数据的参数估计已成为高斯混合聚类的一个重要热点问题.
删失数据的处理方法常基于缺失数据的处理机理.因数据缺失机制不同,处理方法也不尽相同.数据缺失可以分为随机缺失(Missing at random,MAR)和非随机缺失(Missing not at random,MNAR)两大类[12].大多数传统的缺失数据处理方法主要集中于使用样本抽样推断、贝叶斯推断和似然法推断[13].其中贝叶斯推断和似然法在实际数据中的应用更为普遍.当评估项目的长期性能数据随机缺失且观测数据也随机缺失时,使用样本抽样估计数据集分布参数可以忽略缺失机制.当数据属于随机缺失且缺失机制参数不同于数据集分布参数时,使用贝叶斯推断和似然法也可以忽略缺失机制.文献[12]对非随机缺失问题的探索,还包括不可忽略性无响应问题、不可忽略性缺失性问题,甚至被称为有信息缺失的问题等.文献[14]认为存在解决非随机缺失的方法,但是通常难以检验,为此提出了惩罚验证标准,通过惩罚未知参数过多的模型来防止模型过拟合.删失数据作为一种非随机性缺失数据[15−16],因其缺失机制(如删失)的特殊性而不能直接使用一般的非随机缺失方法直接计算[11].
删失数据常包括右删失和区间删失等类型.对于右删失数据,文献[17]基于一类广义概率测度的误差一致性,提供了适用于删失数据的分类支持向量机并应用于删失数据平均值、中位数、分位数的估计以及分类问题.针对区间删失数据,文献[15]提出一种贝叶斯非参数化方法进行概率拟合.文献[18]基于左截断右删失数据构造了分位差的经验估计,并提出了分位数差的核光滑估计.针对删失混合数据,文献[19]提出了一个加权最小二乘估计的一般族,并证明了现有的一致非参数方法属于这个族,识别其估计量并分析其渐近性质.而在高斯混合聚类模型算法中,一般假设观测值的特征向量对聚类有相同的权重[20].然而文献[1]认为高斯混合聚类模型的每一个特征向量的权重并不一样,提出竞争性惩罚期望最大化算法.该算法将特征选择模型和高斯混合聚类模型结合在一起,使用马尔科夫毯滤波器消除多余的特征项,找到最小的相关特征子集,同时确定高斯混合模型的混合成分个数.文献[21]提出了一种基于高斯混合聚类和模型平均的算法.对于缺失值,该方法将每一组成成分得出的估计值作为线性组合的概率估计权重,最终结果是混合成分的估计值的平均值.文献[2]讨论高斯混合聚类分析的过拟合问题.该文献改变了以往认为不相关变量必须通过线性回归方程依赖整个相关变量的做法,认为相关变量并不一定要解释所有的不相关变量.该模型可以有效地提高聚类算法的性能且变量选择的实现基于一个向后逐步算法.标准期望最大化(Expectation-maximization,EM)算法作为高斯混合模型中常用的缺失数据处理方法[22],更适用于处理随机缺失数据.本文在标准EM 的高斯混合聚类算法(EMGM)基础上,提出了嵌套删失数据期望最大化的高斯混合聚类算法(cenEMGM).
本文主要解决非随机缺失下的删失数据因利用率不高而导致聚类准确度不高的问题.本文的主要贡献是:利用高斯混合模型聚类算法独有的特性,在标准EM 算法的基础上提出改进算法cenEMGM,并揭示了删失率对模型算法的作用机制.将删失数据和高斯混合模型聚类算法结合,更加准确地处理删失数据.通过调整删失数据的分布函数,使得删失数据最大期望算法不断更新均值、协方差和混合系数的估计值,从而使得聚类簇中心不断接近真实的簇中心.cenEMGM 算法在标准EMGM 算法的基础上进行改进,该方法更加灵活,对删失和未删失数据采取不同的处理方式.删失数据EM 算法和高斯混合聚类相结合,使得该方法比原方法聚类效果更好,准确性更高.后续章节结构如下:第1 节引入高斯混合聚类模型.第2 节论述删失型缺失数据的相关概念.第3 节构建高斯混合聚类的参数估计算法,包括标准EMGM 算法和cenEMGM 两种算法,以及两个模型校验准则.第4 节使用数值实验验证算法.第5 节得出结论.
1 高斯混合聚类模型
对d维数据空间 Rd中,随机变量y的观察值为一个由n个样本构成的数据集,D={y1,y2,···,yn},其中yi为其第i个样本.并将第j维数据记为y(j).假设样本生成过程由包含K个成分的高斯混合分布确定.第k个成分fk的参数为 Θk=(πk,µk,Σk);其中,πk为其混合系数,µk为均值,Σk为方差.全部参数 Θ={Θ1,Θ2,···,ΘK}.y(j)为其第j维观测值.对于y,定义高斯混合分布[20]如下:
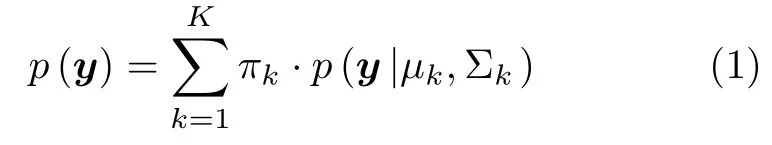
其中,K为混合成分数量,且每个混合成分对应一个高斯分布 N(µk,Σk),相应的“混合系数”πk >0,.
样本生成过程中,记π={π1,···,πK},首先根据π定义的先验分布选择高斯混合成分,且选择第k个混合成分的概率为πk;然后,根据被选择的混合成分的概率密度函数进行采样,从而生成相应的样本.
在高斯混合聚类模型中,类似地存在K个簇,C={C1,C2,···,CK}.将yi是否被划分到簇Ck中的随机变量记为,簇指示变量∈{0,1}.当yi被划分到簇Ck时,=1,意味着yi{由fk生成;否则=0.对于N个样本总体,表示第k个 (k=1,2,···,K)高斯混合成分生成样本y的指示变量值.因此,对于i=1,2,···,N,=1的概率对应于πk.根据贝叶斯定理,的后验分布对应于
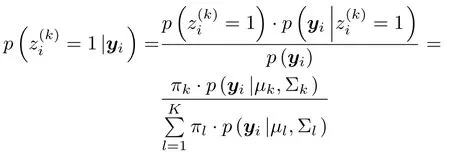
当高斯混合分布(1)已知时,高斯混合聚类将把样本集D划分为K个簇,样本yi的簇标记λi.

可见,高斯混合聚类的本质是采用概率模型(高斯分布)对原型进行刻画,簇划分则由原型对应后验概率确定.因一个簇对应一个中心点,隶属于每一个簇C的数据样本将聚类在簇中心点附近.高斯混合聚类模型效果越好,所估计的簇中心点与实际簇的中心点之间距离将越小甚至重合.
2 删失型数据缺失机制
2.1 数据缺失机制
依据文献[12]将数据缺失机制分为四种类型,包括随机缺失、完全随机缺失、取决于未被观测因素的缺失(可以通过未被观察或记录的数据进行预测的)以及和仅依赖于缺失值自身的缺失机制.后两种缺失机制即为这里将定义的非随机缺失.
在数据空间 Rd中,令A为一个实数集合,设为一个指示变量,表示y的元素在集合A中是否存在观察值.若∈A,则=1,否则=0.这里yi不区分变量及其真实值,而将其观测值记为.令作为yi中不存在缺失的部分,表示yi中存在缺失值的部分,那么.
定义1.如果对所有和参数 Θ,
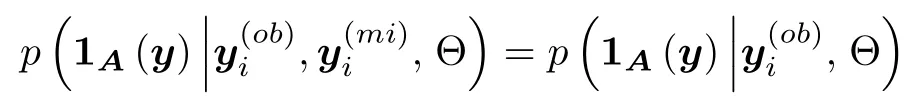
则缺失数据机制为随机缺失.
定义2.如果对所有和参数 Θ,
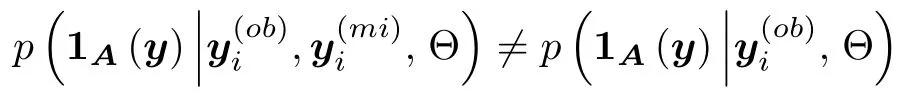
则缺失数据机制为非随机缺失.
可见,对于随机缺失数据,其样本数据及指示变量满足交换性,而非随机缺失数据不满足这一性质[12].当缺失数据是随机缺失时,可直接使用标准EM 算法、多值插补、回归等方法揭示缺失机制.下面引入一类非随机性缺失数据,即删失数据,并研究其缺失机制和参数估计方法.
2.2 删失数据的似然函数
这里给出删失数据的定义,并详细阐述删失数据的缺失机制和似然函数.在数据空间 Rd中,[a,b]d为一个超矩阵[11],其中上边界b=(b(1),···,b(d))T,下边界a=(a(1),···,a(d))T.
定义3.删失数据(Censored data)是指yi的观测值满足分段函数:

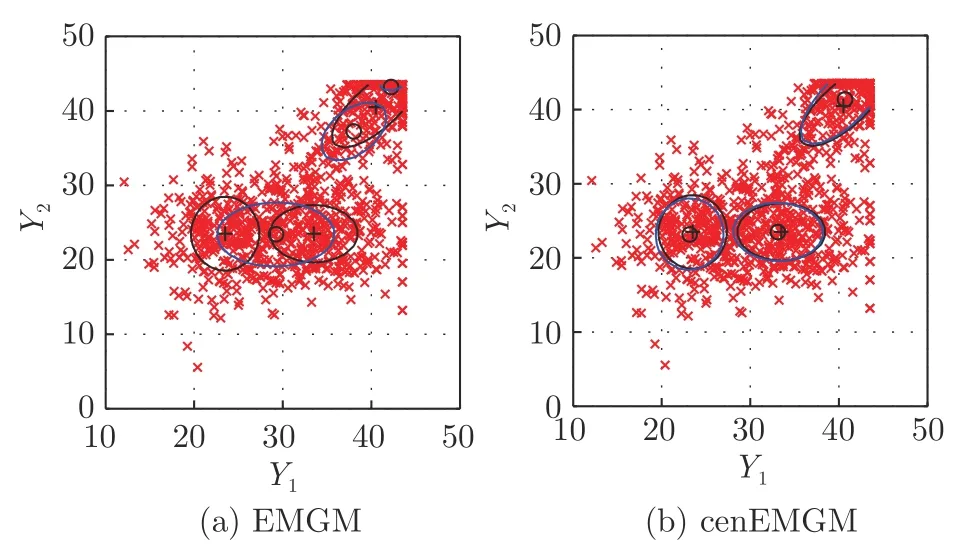
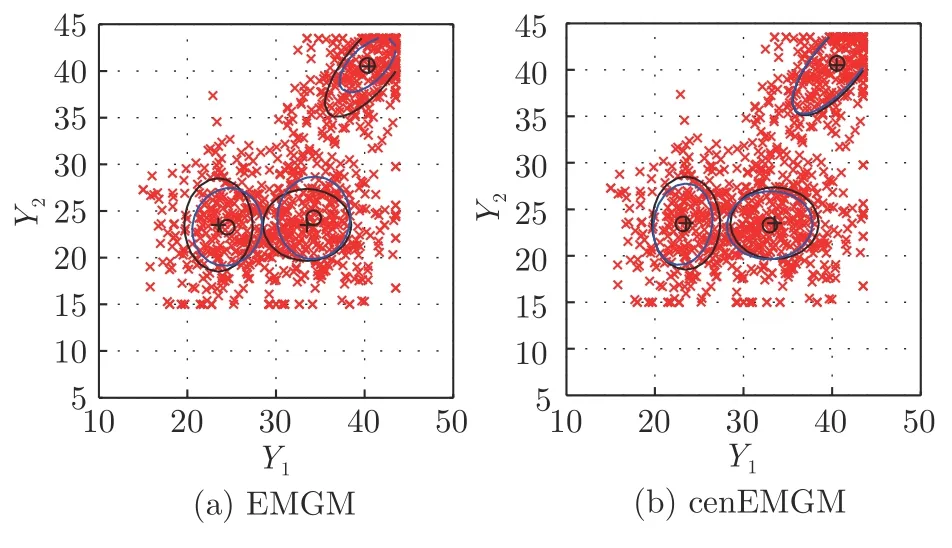
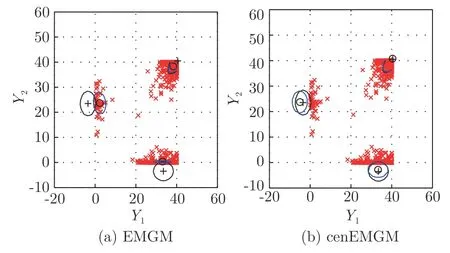
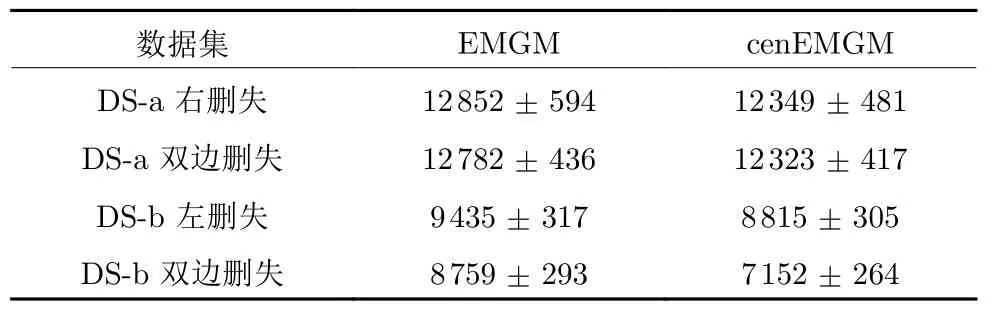
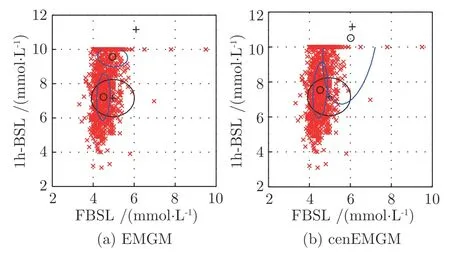
其中,a 换言之,yi中的缺失部分被分别赋予a或b对应维度上的元素值.为分析概率密度和估计参数,假设的元素个数为J1,的元素个数为J2,且J1+J2=d.不妨进一步假设,.对于删失数据,A=[a,b]d.为简化,令δij=1−,当δij=1时,表示因删失而存在缺失数据,其对应观测值被赋予边界值;相应地,δij=0,表示不存在缺失数据,即观测值等同于真实值.y观测值的样本删失率.对于一维数据,删失率pce=nce/n,其中nce是存在删失的样本数. 根据删失数据的定义,y1:n的部分真实值(如序数为n1+1,···,n的值)被修改.那么,其被修改后的数据(不存在缺失部分的值、和缺失部分的修改值)构成新数据集,记为x1:n.对于∀i,∀j,有 与缺失数据机制对应,但因每一个样本yi的删失模式会不一样,而使用im和io分别表示删失和未删失数据的坐标序号集,故分别指删失部分的缺失值(缺失时的真实值)和删失后的改写值(简称删失值),分别指原数据不存在缺失的部分与删失型数据对应的部分值,尽管没有删失时它们值等同.那么.同时,. 为简化,将y的数据空间划分为{Yt|t=0,1,···,T},其中当,此时数据不存在删失;而当,t>0 时,数据发生删失.将删失部分调整后的观测值x的数据空间划分为{Xt|t=1,···,T},注意,这里没有涵盖不存在删失的部分,即x的数据空间划分不涵盖X0.对于yi∈Y0,观测值xi的似然函数如下: 而对于yi缺失机制,有,ti >0,其似然函数如下: 并且关于f(xi)推导式(4)的右边部分转化为: 高斯混合聚类参数估计主要包括成分的期望、方差和对应的混合系数.嵌套标准EM 的高斯混合聚类算法,这里简记为EMGM.并将针对删失数据所提出的改进算法,即嵌套删失型数据期望最大化的高斯混合聚类算法,简记为cenEMGM 算法. 对于独立观测变量集合y1:n,参数空间 Θ,第k个成分fk和簇指示变量,对数似然函数为: 其中,Θk=(πk,µk,Σk)表示第k个成分的参数,(Σk)−1表示 Σk的倒数,Const表示常数,tr(·)表示矩阵的迹,In表示值全为1 的 1×n向量. 根据标准的期望最大化算法[23],其假设为数据存在随机缺失.对于独立观测变量集合y1:n,Θ,Θold和 Θnew分别为参数空间,算法中更新前的参数及更新后的参数. 算法第一步(步骤E):计算期望函数Q(Θ;Θold)=,步骤E 可以简化为计算条件概率: 第二步(步骤M):寻找新的参数集 Θnew,使得Θnew=arg maxΘQ(Θ;Θold).更新后的参数Θnew=,形成一个更新的闭环形式: 该算法不断迭代E 步和M 步,直至收敛.以最后获得的更新参数作为 Θ 的最优估计值. 引理1.通过最大似然估计方法获得全数据的参数,即求解全数据得分向量方程(yi,Θ)=0,得到 其中,IF(Θ)为全数据信息矩阵,IF(Θ)=E[SF(D,Θ)(D,Θ)]. 通过正则渐近线性法(Regular and asymptotically linear,RAL)[24]获得全数据的参数记为,即求解全数据得分向量方程=0. 引理2.对于RAL 方法估计的参数,应满足: 对于 arg maxΘQ(Θ;Θold),根据全数据参数估计的引理,存在关于期望最大化算法估计删失型缺失数据的定理. 定理1.令全数据D={y1,y2,···,yn},对应的删失型缺失数据,对缺失数据使用逐步更新的EMGM 算法估计参数,可通过以下方程求解. 依据第3.2 节给定删失数据及其似然函数,cen-EMGM 算法首先计算完全对数似然函数的期望: 该式子可以由式(4)进一步推导出结果. 结合高斯混合分布定义(1),针对y(mi)的条件概率分布,,推导其条件分布期望.因为是正态密度函数且满足 条件密度fk(y(mi)|x)是在Xc上的截尾正态密度函数,那么计算关于Qc的充分统计量: 定理2.全数据D={y1,y2,···,yn},对应的删失型缺失数据,在给定缺失数据和RAL 估计参数下的原数据的得分向量,对缺失数据使用cenEMGM 算法估计参数,满足 其中,IF(Θ)为全数据信息矩阵,Θ 为数据的真实参数,对于cenEMGM 算法. 证明.因cenEMGM 算法中删失数据的对数似然函数期望为,那么其得分向量的期望 故而有 又因为 所以有 根据定理2 获得对数似然函数的期望Qc关于Θ最大化的解,即得到了Θ(t)=ar g maxΘQc(Θ;Θ(t−1))的优化解,.该算法的步骤t≥1,并且 Θ(0)表示初始值,可通过K-means 聚类方法获得赋值.求解的高斯混合聚类的混合系数πk为: 同时,µk和 Σk关于 arg maxΘQc(Θ;Θ(t−1))的优化解分别为: 式(13)~(15)作为标准EM 算法式(6)~(8)针对删失型缺失数据的改进.式(13)与(6)在形式上没有变化,从理论上论证了删失型算法cenEMGM与标准算法EMGM 在混合系数上一致.式(14)与(7)相比较发现,在删失数据算法cenEMGM 中,y1:n的删失部分被条件均值代替.式(15)与(8)相比较发现,删失数据算法cenEMGM 的被样本校正协方差所替代.标准算法EMGM 即为算法cenEMGM 处理不存在删失数据时的特定情形. 为了防止算法出现过拟合并计算估计值和真实值之间的距离,需要设定模型检验准则.这里引入信息散度(Kullback-Leibler divergence,KLD)和赤池弘次信息准则(Akaike's information criterion,AIC)[20,25].信息散度KLD 公式[25]为: 其中,p(y) 是y真实分布的概率密度函数,q(y)是y估计分布的概率密度函数.本文中y的概率密度函数由高斯混合分布(1)确定..在算法EMGM 中,p(y)由式(6)~(8)确定;在算法cenEMGM中,q(y)由式(13)~(15)确定. 对于AIC 准则,其值最小的模型即为最佳模型.假设模型的误差服从独立正态分布,AIC 可表示为: 其中,N(Θ)是模型算法参数的数量,d为D数据维度,K为高斯混合模型的成分数量,L(Θ)是参数集 Θ 的似然函数. 嵌套删失型数据期望最大化的高斯混合聚类算法(cenEMGM)主要由高斯混合聚类和针对删失数据的期望最大化算法构成,如算法1 所示.第1)步初始化参数,常使用k-means 算法.第2)~10)步,运行直至满足停止条件,跳出循环.其中第3)~4)步,cenEMGM 算法的E 步,计算后验概率;第5)~9)步,cenEMGM 算法的M 步,计算新的模型参数.第11)~13)步,划分簇.算法流程的停止条件是,其中ε是一个小的正数(如1.0×10−6).其中,,k=1,2,···,K.cenEMGM 算法的计算复杂度(时间复杂度)受到样本规模n和参数规模影响,其中d为D数据维度,K为高斯混合模型的成分数量. 算法1.嵌套删失型数据期望最大化的高斯混合聚类算法cenEMGM cenEMGM 算法的核心步骤主要基于式(13)~(15).与之对应的标准EMGM 算法,其核心是式(6)~(8).cenEMGM 算法是针对删失型缺失数据的改进算法,先根据新均值向量计算新样本规模,然后计算新混合系数.因为样本规模改变,所以样本方差、删失率、观测数据均值等参数同步做出改变.针对删失数据修改的这些内容,使cenEMGM 算法更灵活,更能适应含有删失数据的高斯混合聚类. 高斯混合分布中,πk是选择第k个混合成分的概率,由式(8)和式(13)可以看出,样本删失率间接地通过样本容量影响着πk,所以pce对πk产生影响.数据质量可以衡量采样机制产生的选择偏差程度[26],其不仅和估计准确度有关,更是与删失率有关.为了提高模型的准确性,可以根据删失率调整并确定样本规模n.关于样本规模在实验设计中已有讨论[27].这里给出样本方差未知时删失率pce与样本规模n的结论.根据统计推断理论,检验水准α时,预测能力 (1−β)表示,当所考虑的总体与原假设H0确有差别时,按照检验水准α能够发现拒绝它的概率.总体方差未知时,在删失数据缺失率为pce的情况下,估计样本容量大小如下:n0=,其中δ表示估计精度(即允许误差),为数据分布中的真实缺失率,t为检验统计量.对于一定规模的同一数据集,随着样本删失率pce上升,参数估计模型的估计能力下降,导致准确性也降低.因此,数据分析中要求样本容量不小于n0.随着数据感知和收集成本下降,数据可得性变高,统计机器学习模型使用的数据规模选取常会超过模型的测试能力要求,且通常会考虑数据的缺失机制[12]. 这里使用人工数值实验与真实数据分析,验证方法的有效性. 实验从预设分布生成数据集,并对数据进行删失处理.在删失数据上,分别采用嵌套标准EM 的高斯混合聚类算法EMGM 和嵌套删失型数据cenEM 的高斯混合聚类算法cenEMGM 进行实验分析.实验结果通过聚类的真实参数与估计参数比较、KL 散度等统计指标进行比较分析. 为在多变量上比较算法,这里设计两个含有三个成分的二元高斯混合模型的实验.在两个实验中,实验数据集D S-a 的观测值 (Y1,Y2)被设置在[10,50]×[5,45]的矩形窗中,用于右删失型数据和双边删失型数据在EMGM 算法和cenEMGM 算法上的实验;实验数据集DS-b 的观测值 (Y1,Y2)被设置在 [−20,60]×[−10,60] 的矩形窗中,用于左删失型数据和双边删失型数据在EMGM 算法和cenEMGM算法上的实验.右(左)删失型缺失是指在变量值域范围内,设定了观测值上(下)界,且大(小)于该上(下)界的其他值被赋予该上(下)界值,但并无给定的下(上)界.双边删失型缺失是指在变量值域范围内,同时设定了观测值上界和下界值,大于该上界的其他值被赋予该上界值,且小于该下界的其他值被赋予该下界值.这里生成的两组数据分别采用了两种删失机制,并非只讨论一组数据的左删失、右删失及双边删失,以便体现删失数据边界的多样性和实验的可重复性. 在实验数据集DS-a 中,三个分量的中心都在对应的矩形窗内,参数设置如下:成分权重为π=(0.25,0.40,0.35);均值为µ1=(23.50,23.50),µ2=(33.50,23.50),µ3=(40.50,40.50);方差中,成分1 与成分2 在两个变量之间不存在相关性: 成分3 的两个变量之间存在相关性: 在实验数据集DS-b 中,虽然三个成分的中心都在对应的矩形窗内,但有两个成分的中心落在了下界之外.参数设置如下:成分权重和方差分别与实验数据集DS-a 对应一致.但它们的均值分别为µ1=(−3.50,23.50),µ2=(33.50,−3.50),µ3=(40.50,40.50). 在每种情形下绘制1 000 个数据点后,根据删失型缺失的预设边界,边界外的所有数据都删失.在DS-a 中,针对右删失缺失型数据,其上界值设为43.5,表明删失类型的(超)矩形窗为[10,43.5]×[5,43.5],其中10 和5 为小于其观测值最小值的一个数,来源于观测值的矩形窗下界,并不表示删失数据的下界,并观察到约862 个数据点未删失,并使用EMGM 算法和cenEMGM 算法进行实验,如图1 所示;若其还存在左删失,如将其下界值设为15,形成双边删失型缺失数据,表明删失类型的(超)矩形窗为 [15,43.5]×[15,43.5],约818 个数据点未删失,如图2 所示.类似地,在DS-b 中,针对左删失缺失型数据,其下界值设为0,表明删失类型的(超)矩形窗为 [0,60]×[0,60],其中60 为大于其观测值最大值的一个数,来源于观测值的矩形窗上界,并不表示删失数据的上界,约484 个数据点未删失,如图2 所示;若其还存在右删失,例如其上界值设为40,形成双边删失型缺失数据,表明删失类型的(超)矩形窗为 [0,40]×[0,40],约241 左右的数据点未删失,如图3 所示.图中小十字表示删失后的数据点,‘o’ 和实心椭圆是每个成分在算法估计后的聚类中心和距离为1 的等高曲线.其距离使用成对马氏(Mahalanobis)距离计算.‘+’ 和虚线椭圆表示高斯混合模型成分的真实聚类中心和等高曲线. 图1 在数据集DS-a 右删失上的两种算法比较Fig.1 Comparison of the two algorithms on the dataset DS-a with right censoring 图2 在数据集DS-a 双边删失上的两种算法比较Fig.2 Comparison of the two algorithms on the dataset DS-a with double-side censoring 图3 在数据集DS-b 左删失上的两种算法比较Fig.3 Comparison of the two algorithms on the dataset DS-b with left censoring 图1 显示EMGM 算法和cenEMGM 算法在二维合成数据DS-a 右删失上的实验结果.EMGM 算法在该数据集上的结果(图1 (a))显示,‘o’ 和实心椭圆所表示的估计的聚类中心和距离为1 的等高曲线与 ‘+’ 和虚线椭圆表示高斯混合模型成分的真实聚类中心和等高曲线之间存在显著差异.而cenEMGM 算法在该数据集上的结果(图1(b))显示,cenEMGM 算法估计的聚类中心和等高曲线与真实聚类中心和等高曲线之间的差异明显减小,其结果明显优于EMGM 算法. 图2 显示EMGM 算法和cenEMGM 算法在二维合成数据DS-a 双边删失上的实验结果.EMGM算法在该数据集上的结果(图2 (a))显示,聚类中心和距离为1 的等高曲线比EMGM 算法(图1 (a))明显更接近于真实值.因为这里除了存在右删失外,还存在左删失.尽管缺失率更高,但观测到的数据(未删失部分)的均值更接近真实值.同时可见,cenEMGM 算法估计(图2 (b))的聚类中心和真实聚类中心之间的差异也明显更小,其结果进一步表明cenEMGM 算法在处理删失数据聚类问题上明显优于EMGM 算法. 图3 显示EMGM 算法和cenEMGM 算法在二维合成数据DS-b 左删失上的实验结果.‘+’ 表示高斯混合模型成分的真实聚类中心,其中两个已落在了值域的下界之外.EMGM 算法的结果(图3 (a))显示,其估计的聚类中心(‘o’)和等高曲线(实心椭圆)没有超出值域的下界,表明估计值与对应的真实值之间存在显著差异.而cenEMGM 算法的估计结果(图3 (b))显示,其估计的聚类中心和等高曲线与真实值之间的差异明显更小.对于图3 (b)图中靠近Y2坐标轴的成分,尽管其估计值与真实值之间尚存在一些差异,但这一差异与EMGM 算法所表现出的差异已经小很多,且另外两个成分的估计值与真实值之间几乎无差异,因此这些结果进一步表明cenEMGM 算法在这类数据聚类上更优于EMGM 算法. 图4 显示EMGM 算法和cenEMGM 算法在二维合成数据DS-b 双边删失上的实验结果.三个成分的聚类中心真实值(‘+’)都在下界或上界之外.EMGM 算法在该数据集上的结果(图4 (a))显示,三个成分的估计的聚类中心和距离为1 的等高曲线与真实值之间都存在显著差异.与此相反,cenEMGM算法在该数据集上的结果(图4 (b))显示,其估计值也可以位于上下界之外,更接近真实聚类中心和等高曲线,即估计值与真实值之间的差异明显变小.结果表明cenEMGM 算法在处理这类删失数据聚类时明显优于EMGM 算法. 图4 在数据集DS-b 双边删失上的两种算法比较Fig.4 Comparison of the two algorithms on the dataset DS-b with double-side censoring 此外,进行 100 次重复实验,记录多次实验结果在KLD 值与AIC 值上的平均值和方差.实验合成数据集真实分布和估计分布之间的KLD 值见表1,对于参数估计的两种算法AIC 值比较见表2.结果表明,对于两种算法在同一数据集上的表现,不论是KLD 值还是AIC 值,cenEMGM 算法的值都小于对应EMGM 算法的值,说明在删失型缺失数据参数估计上cenEMGM 算法优于EMGM 算法.对于同一算法在不同数据集上的表现,因双边删失比对应的单边删失因缺失而拥有更少的样本数据,双边删失的AIC 值小于对应的单侧删失的AIC 值. 表1 实验合成数据集真实分布和估计分布之间的KLD 值Table 1 Kullback-Leibler divergence (KLD)between the true densities and the estimated densities of the synthetic data set 表2 实验合成数据集参数估计的两种算法AIC 比较Table 2 AIC comparison of the two estimation algorithms on the synthetic data set 数据来源于某大型医院信息系统中的临床数据[4].这些数据样本包括554 个相关属性,其中有106 个建档属性、23 个检验数据属性、157 个来自实验室信息系统的试验结果属性以及268 个电子健康档案中病案首页的属性.根据医学领域专家意见和文献进行属性筛选,经过数据清理后所得数据集包括50 个属性,具体包括年龄、婚龄、孕妇体重指数、红细胞计数、谷氨酰转肽酶、空腹血糖水平值等属性.根据验证的目的,这里所使用的数据集为原临床数据集中提取的包含4 个属性的数据.这些属性具体为关于孕妇在筛检妊娠期糖尿病过程中的血糖水平值和医生给出的诊断结果,即是否患有妊娠期糖尿病.其中包括关于血糖水平值的3 个属性分别为口服糖耐量试验中的空腹血糖水平值(Fasting blood sugar level,FBSL)、1 小时血糖水平值(1h-blood sugar level,1h-BSL)和2 小时后的血糖水平值.根据国际妊娠合并糖尿病研究组织建议,妊娠期糖尿病的诊断标准为[4],空腹血糖水平值高于5.1 mmol/L、1 小时血糖水平值高于10 mmol/L 和2 小时血糖水平值高于8.5 mmol/L,满足以上三项中的任一项即诊断为患有妊娠期糖尿病,数据记录聚类为患病簇,否则为正常簇.在电子病历记录与数据联结整合中,小于等于10 mmol/L 的血糖水平值记录为原始测量值,而高于10 mmol/L 的空腹血糖水平值和1 小时血糖水平值的数据被记录为“>10mmol/L”型删失型数据.虽然这些删失型数据能够为诊断结果提供直接的临床证据,但是这些数据的删失对于进一步探索关于妊娠期糖尿病的风险因子,以及这些因子对血糖水平值影响的因果关系研究构成困难.又因妊娠期糖尿病的主要治疗方案包括膳食改变、增加锻炼甚至胰岛素等的药物治疗[28],但这些治疗方案对以血糖水平值作为结果的影响作用大小是有差异的.为后续研究这些影响作用,在使用这些删失型的血糖水平值数据时,需要对这些数据的分布参数进行较为精确的估计.本文的聚类算法正是针对这些删失型数据提供分布参数的估计. 从原数据中选择了917 例数据进行数值计算,其中756 例样本属于正常簇,161 例样本属于患病簇.在917 例样本数据中,以空腹血糖水平值和1小时血糖水平值进行分析,发现78 例样本数据属于删失型数据,主要存在于1 小时血糖水平值上.对这一数据集,分别采用EMGM 算法和cenEMGM算法进行高斯混合聚类,结果如图5 所示. 图5 在血糖测试数据右删失上两种算法比较Fig.5 Comparison of the two algorithms on the dataset of blood sugar tests with right-side censoring 图5 显示了EMGM 算法和cenEMGM 算法在删失型血糖水平值数据上的聚类结果.横坐标为空腹血糖水平值,纵坐标为1 小时血糖水平值,其样本数据关于“>10 mmol/L”删失.真实数据中一个成分的聚类中心真实值(‘+’)在样本数据所展示的范围内,为(4.96,7.16);另一个成分的聚类中心真实值(‘+’)在样本数据的上界之外,为(6.09,11.16),即中心值在1 小时血糖水平值上“>10 mmol/L”.图5 (a)显示EMGM 算法在该数据集上存在一个成分的估计聚类中心和距离为1 的等高曲线与真实值之间存在显著差异,即估计值所在的聚类中心在1 小时血糖水平值以下,而真实值所在的聚类中心在1 小时血糖水平值以上.不同的是,图5 (b)显示cenEMGM 算法在该数据集上的估计值也可以位于上界之外,使得其更接近真实聚类中心,说明估计值与真实值之间的差异明显变小.在模型检验准则上,对于这一真实数据集,EMGM 算法在真实分布与估计分布之间的KLD 值(12.7)高于cenEMGM算法的KLD 值(9.1),同时后者的AIC 值(4 263)低于前者的AIC 值(4 366).因此,这些结果说明cenEMGM 算法在处理真实的删失数据聚类时优于EMGM 算法. 此外,为进一步验证方法的有效性,对于真实数据调整删失率进行拓展,动态改变删失率而进行计算,并对聚类中心、AIC 与KLD 值进行定量对比,如表3 所示. 表3 真实数据及其拓展数据的两种算法比较Table 3 Comparison of the two algorithms with the real data and its extended data 表3 结果表明,当右侧删失率从8.51%增加到11.67%时,两种算法的聚类中心估计值与真实值(4.96,7.16)和(6.09,11.16)之间的差异增大,KLD 值与AIC 值减小.cenEMGM 算法的KLD 值与AIC 值比EMGM 算法的对应值小,说明其在处理删失数据聚类时仍然优于EMGM 算法.当将数据拓展为双边删失型数据时,即在右边删失的基础上增加左边删失6.54 %,总体上删失15.05 %时,两种算法的聚类中心估计值与真实值之间的差异进一步增大,且KLD 值增大而AIC 值减小.总体上,随着删失率的增加,算法处理的能力在一定程度上逐渐减弱,但是cenEMGM 算法的聚类中心估计值与真实值相对更接近,且KLD 值与AIC 值比EMGM算法的对应值更小,进一步说明其通过聚类在处理删失数据的参数估计时仍然优于EMGM 算法. 删失型数据处理特别是在机器学习或数据挖掘等数据处理中,作为工程实践和管理中数据处理的焦点问题.由于删失数据处理的知识有限性,需要根据删失模式制定合适的算法模型.尽管当前数据智能处理所面临的数据规模较大,但选取高价值的实验数据或稀有事件等所面临的删失数据处理仍然显得较为重要.然而,现有的缺失数据处理问题主要集中在随机缺失,对非随机缺失下的删失型数据研究不深,因此本文根据估计算法的有效性理论,针对删失数据期望最大化的高斯混合聚类算法(cenEMGM),通过关于得分向量期望的方程得出算法估计的最优参数.与嵌套标准EM 的高斯混合聚类算法(EMGM)相比,本方法根据删失数据的指示变量调整样本似然函数,进而改进参数估计的期望最大化算法,使得高斯混合聚类模型参数估计准确性更高,AIC 信息准则值更小,聚类效果更好.并通过数值实验论证了本方法相对于EMGM 算法的优越性.更多类型数据中的删失型缺失机制(模式)识别、不同删失情形下多种算法有效性分析及其高斯混合聚类算法拓展是下一步工作重点.



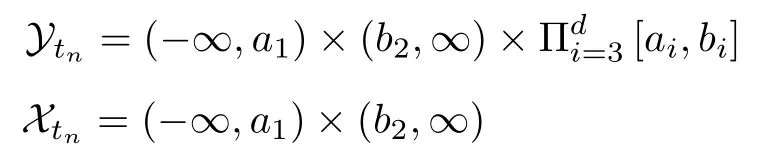
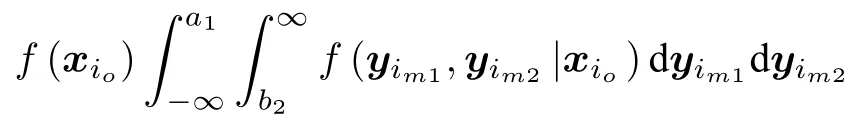
3 高斯混合聚类的参数估计
3.1 基于高斯混合聚类的标准算法EMGM


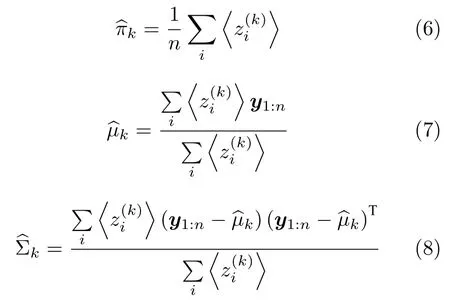
3.2 估计算法的有效性
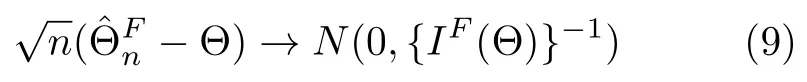




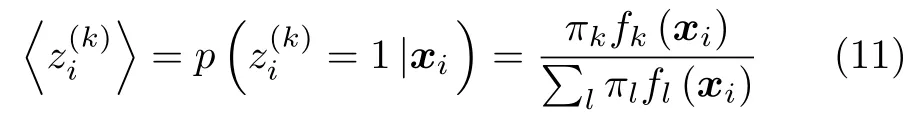
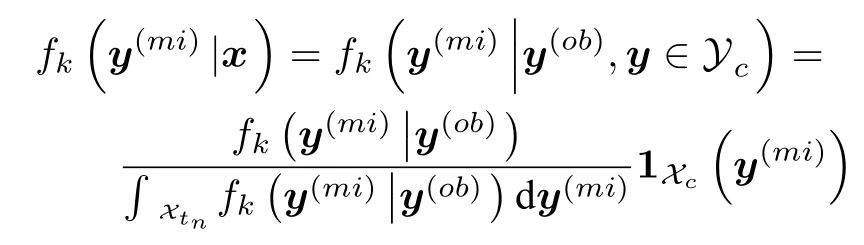
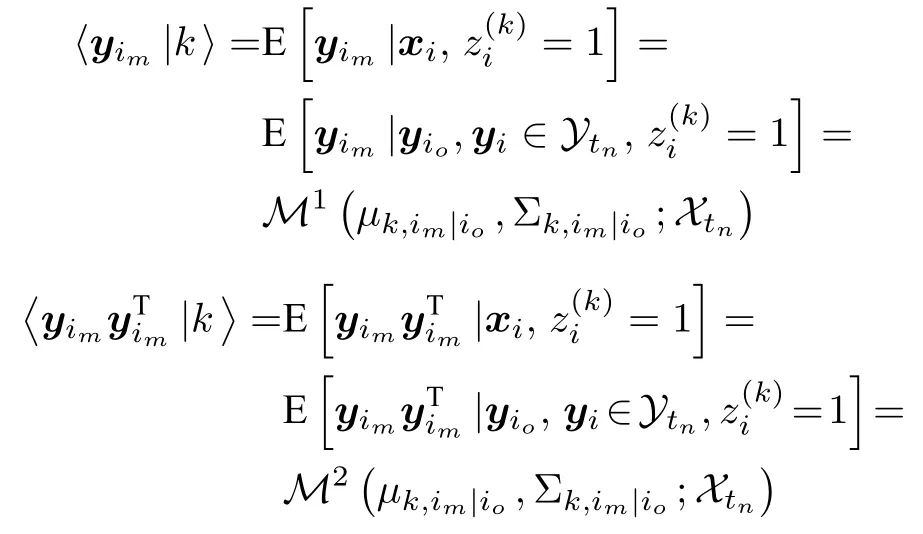
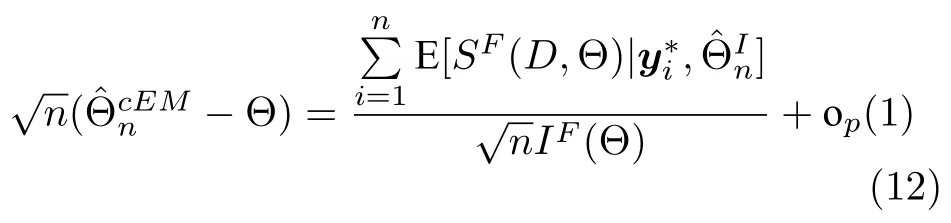
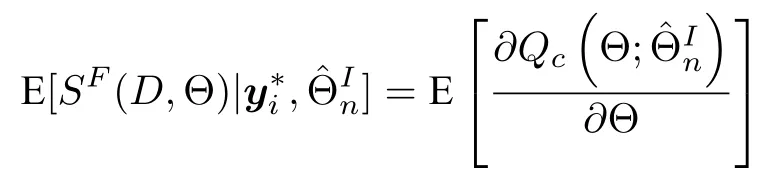


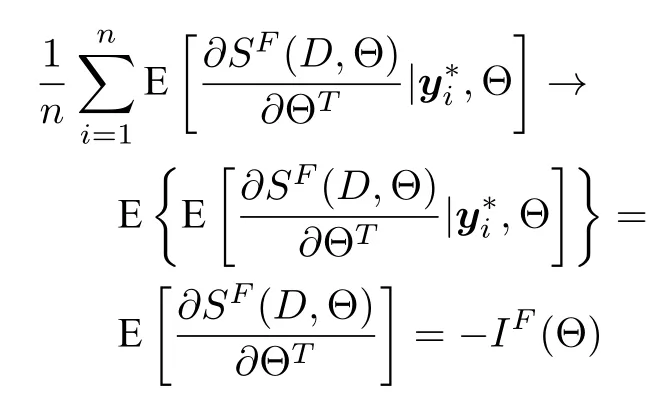

3.3 针对删失数据的算法cenEMGM


3.4 模型检验准则
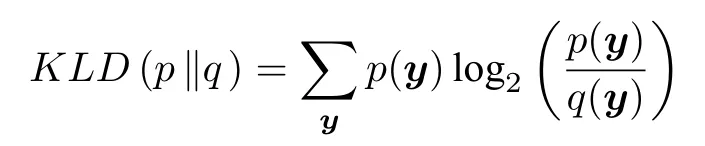
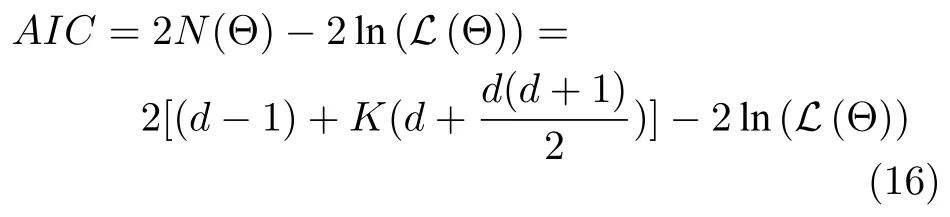
3.5 cenEMGM 算法及分析
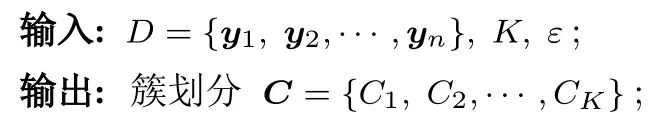

4 数值实验分析
4.1 人工数值实验分析




4.2 真实数据分析

5 结论
