基于机器学习的信息物理系统安全控制
2021-07-25马书鹤马奥运张淇瑞夏元清
刘 坤 马书鹤 马奥运 张淇瑞 夏元清
信息物理系统(Cyber-physical systems,CPSs)是计算单元与物理对象在网络空间中高度集成交互形成的智能系统[1−2].CPSs 广泛应用于水净化与分配[3−4]、智能电网[5]、智能交通[6]和国防军事[7]等重要领域.然而,网络的开放性使得CPSs 极易受到攻击,这对人们的经济和生活产生了巨大危害[8−9].如:2019 年3 月全球最大铝生产商挪威海德鲁公司的勒索病毒攻击事件,2019 年1 月委内瑞拉水电站的网络攻击事件,2017 年美国制药公司默克的勒索病毒攻击事件,2014 年美国波士顿儿童医院的大规模分布式拒绝服务攻击事件等.因此,研究CPSs 安全相关的理论和技术刻不容缓.
常见的研究CPSs 安全问题的方法有:Lyapunov 方法[10−11]、最优化方法[12−13]、博弈论方法[14]等.近年来,人工智能、云计算等技术的发展,为解决CPSs 的安全问题提供了新的途径和方法.不过,值得注意的是,现有的大部分研究成果主要着重于攻击的检测和识别,如:Vu 等[15]利用K-最近邻算法对网络状态进行分类以主动检测分布式拒绝服务攻击;Kumar 和Devaraj[16]先采用基于互信息的特征选择方法选取网络的重要特征,再将它们作为反向传播神经网络(Back-propagation neural network,BPNN)的输入用以识别系统中各种类型的入侵事件;Nawaz 等[17]和Esmalifalak 等[18]利用支持向量机(Support vector machine,SVM)算法检测智能电网中的虚假数据注入攻击;Kiss 等[19]利用高斯混合模型算法对田纳西 − 伊士曼过程中的传感器测量值进行聚类,并选取轮廓系数作为评价指标有效识别攻击;Inoue 等[3]基于由SWaT 系统产生的时间序列数据(包括正常和攻击数据)对比了深度神经网络(Deep neural network,DNN)和支持向量机(SVM)两种算法的攻击检测效果,整体而言DNN要优于SVM.然而,对于某些情况仅仅做到攻击检测与识别是不够的,还需要考虑对攻击信号进行重构进而设计出合适的安全控制器,以削弱甚至消除攻击对系统造成的影响和危害.
本文利用机器学习技术对攻击信号进行重构,本质上是对从受攻击CPS 中采集到的数据进行拟合回归进而获取攻击策略的过程.常见的机器学习回归方法有:BPNN、高斯过程(Gaussian process,GP)、极限学习机(Exteme learning machine,ELM)、最小二乘支持向量机(Least square support vector machine,LS-SVM)等.文献[20]为了提高非线性系统控制器的控制精度,分别利用BPNN、ELM 和LS-SVM 对系统的未建模动态部分以及线性化误差进行精确估计和补偿,并从算法的训练时长和测试误差角度对三种算法进行了对比,结果表明训练ELM 用时最短,LS-SVM 拟合精度最高.为了改善上述算法各自存在的弊端,在原始算法基础上出现了不同的变体,如:为了改善BPNN 存在的训练速度慢、参数寻优难、过拟合、局部最优以及隐含层节点数人为指定等问题,文献[21]利用引入了自适应学习率和动量项的粒子群优化BP 神经网络(Particle swarm optimization BP neural network,PSO-BP)预测网络流量;为了提高ELM 的稳健性和非线性逼近能力,Huang 等[22]提出了核极限学习机(Kernel extreme learning machine,KELM),并通过实验验证了KELM 比LS-SVM 具有更强的泛化能力.
基于以上考虑,本文利用KELM 重构攻击信号,但是考虑到KELM 同样具有参数敏感性问题,于是选择具有结构简单、调整参数少、计算量小、收敛速度快等优点的果蝇优化算法(Fruit fly optimization algorithm,FOA)对KELM 进行优化.然而,基础的FOA 存在容易陷入局部最优解的问题,因此本文对FOA 进行改进,最终利用基于改进的果蝇优化算法(Improved fruit fly optimization algorithm,IFOA)的KELM 对攻击信号进行重构,将攻击信号视作系统扰动并利用重构的攻击信号对其进行补偿,对补偿后的系统使用模型预测控制(Model predictive control,MPC)策略,并给出了使系统是输入到状态稳定(Input-to-state stable,ISS)的条件.此外,为了验证所提算法的有效性,本文从攻击者角度建立了优化模型用以生成攻击数据.最终,通过数值仿真验证了IFOA-KELM 相较于FOA-KELM、PSO-BP 和LS-SVM 的优越性以及安全控制策略的有效性.
符号说明.Rn表示n维欧几里得空间;In表示n阶单位阵;A>0(A≥0)表示矩阵A是正定矩阵(半正定矩阵);对于列向量x和矩阵P >0,‖x‖表示x的 2范数,表示x的加权范数.
1 问题描述
本文考虑执行器受到攻击或控制信号遭受篡改的CPS,具体如图1 所示.
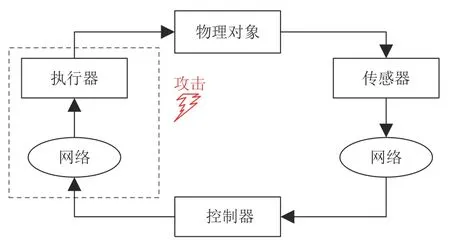
图1 遭受攻击的信息物理系统框图Fig.1 The diagram of the CPS under cyber attack
图1 中的物理对象是线性时不变系统,它的状态方程可表示为

其中,x(k)∈Rn和u(k)=Kx(k)∈Rm分别为k时刻的系统状态变量和控制输入,A,B和K分别为相应的系统矩阵,输入矩阵和状态反馈增益矩阵.
假设攻击者根据系统的状态和控制输入设计攻击策略,则可将受攻击后系统的状态方程表示为

其中,xc(k)和uc(k)分别为受攻击后系统的状态变量和控制输入,矩阵Ba描述了攻击对系统产生的影响,a(k)表示攻击信号,函数a(xc(k),Kxc(k))=Baa(k)为待设计的攻击者策略.
为了获得足够的标记数据用于训练机器学习算法,我们从攻击者角度出发,建立系统的优化模型.
令A1=A+BK,对于攻击者而言,系统的状态方程可表示为

攻击者的目标往往是用较少代价使得系统状态尽量偏离其期望的轨迹,因此可以用如下优化问题来描述攻击者的攻击目标
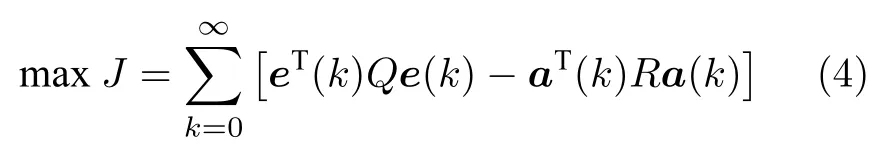
其中,e(k)=xc(k)−x(k)表示系统的状态误差,Q≥0和R≥0 分别为状态误差和攻击信号的加权矩阵.
为了方便求解上述优化问题,定义如下变量
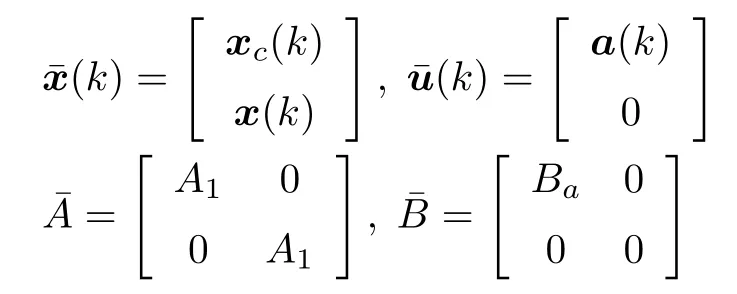
根据式(1)和式(3)可以得到
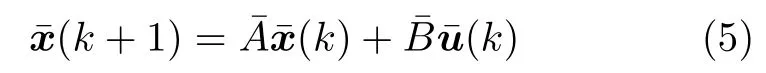
并且可将优化问题(4)转化为
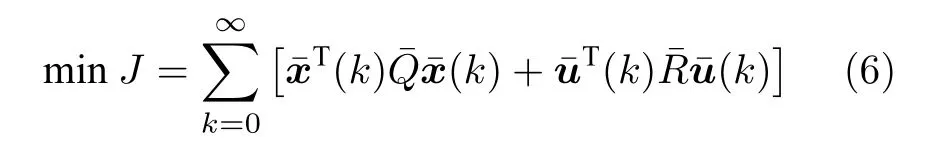
由式(6)可求得最优反馈攻击策略
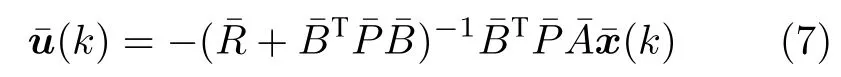


考虑到攻击策略一般不依赖于受攻击前的系统状态x(k),故令P12=0.若满足


结合式(3)和式(13)可以生成一系列的攻击数据以供训练机器学习算法.
2 攻击信号重构算法
本节利用IFOA-KELM 算法对攻击信号进行重构.
2.1 核极限学习机
ELM 是一种前馈神经网络[23],如图2 所示,它由输入层、隐藏层和输出层共三层构成.
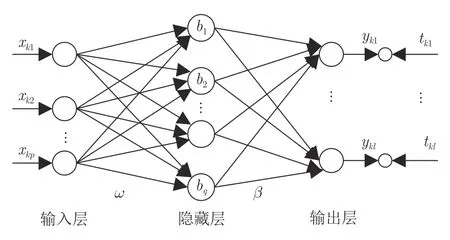
图2 极限学习机结构图Fig.2 The structure of ELM
假设存在N个不同的训练样本,其中,xk=[xk1,xk2,···,xkp]T∈Rp为输入矢量,tk=[tk1,tk2,···,tkl]T∈Rl为期望输出矢量,yk=[yk1,yk2,···,ykl]T∈Rl为输出矢量.将第i个 隐层神经元与输入层之间的连接权重记作wi=[ωi1,ωi2,···,ωip]T,并记w=[w1,w2,···,wq]T.将第i个隐层神经元的阈值记作bi.隐藏层神经元的激活函数为.将第i个隐层神经元与输出层之间的连接权重记作βi=[βi1,βi2,···,βil]T,并记β=[β1,β2,···,βq]T.ELM 的期望目标为,因此
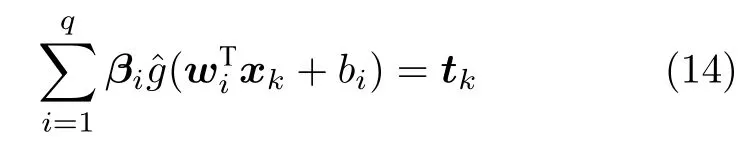
将上式表示成矩阵形式

其中,
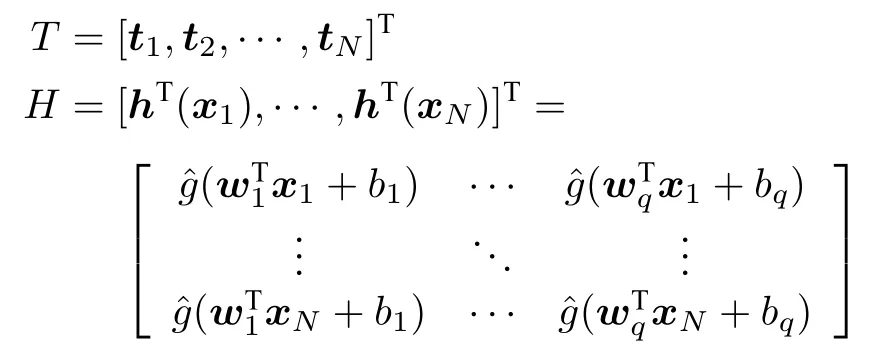
训练ELM 本质上是为了得到β,而根据式(15)可得

在ELM 训练过程中,wi和bi是随机给定的,这可能会导致ELM 的稳健性和泛化能力变差,为了解决上述问题,将隐藏层神经元的随机映射用核映射来代替,即得到KELM[24].现将KELM 中采用的核函数定义为
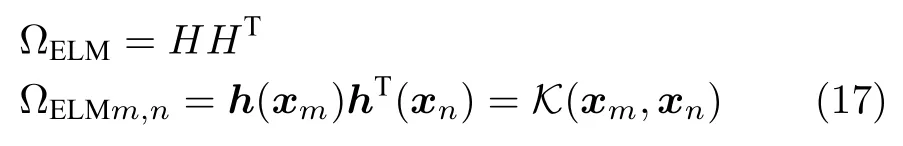
于是,KELM 的输出y可表示为
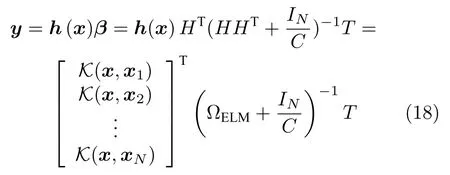
注 1.根据Mercer 定理[25],本文选用高斯核函数作为核函数,即,其中σ是带宽.
由式(18)可知,KELM 中需要调整的参数只有两个:核函数参数σ和惩罚因子C,它们对于KELM的性能起着至关重要的作用.因此,如图3 所示,本文利用FOA 择优选取σ和C,并将两个果蝇群体分别称作σ群体和C群体.
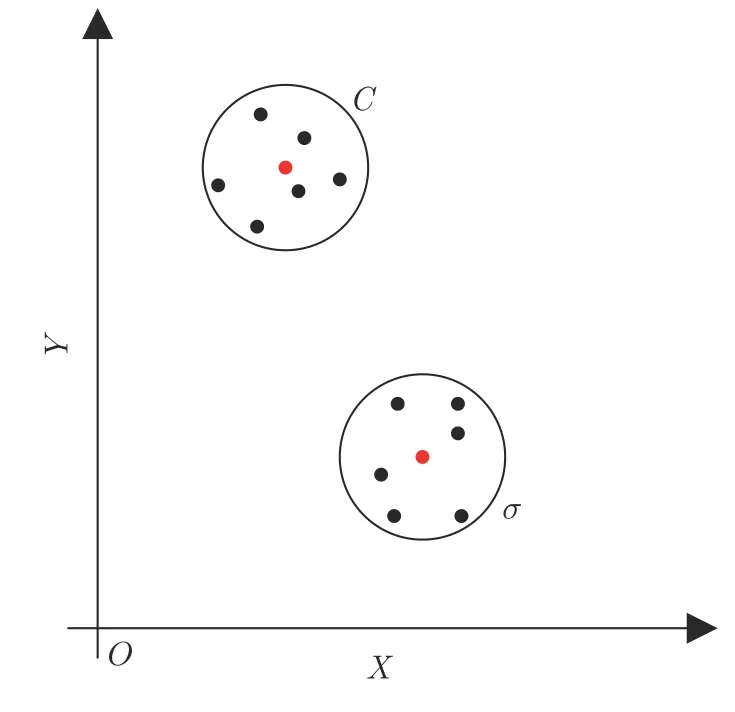
图3 FOA 优化参数Fig.3 The optimization parameter of FOA
2.2 果蝇优化算法
FOA[26]源于果蝇的觅食行为,它和粒子群优化算法[27]、鲨鱼优化算法[28]、细菌群体趋药性算法[29]类似也属于群体智能优化算法的一种.果蝇具有优于其他物种的嗅觉器官和视觉器官,它们的觅食原理如下:首先借助嗅觉器官搜集空气中弥散的各种气味,然后发觉目标大致方位并飞往附近区域,最后利用敏锐的视觉定位目标和群体聚集的具体位置.FOA 具体实现步骤如下:
步骤 1.初始化果蝇群体大小,FOA 最大迭代次数以及果蝇群体位置.
步骤 2.每个果蝇个体按照随机给定的方向和范围搜寻目标位置.
步骤 3.由于果蝇个体事先不知道目标所在的位置,因此以原点作为参考点,计算个体到原点的距离,并将该距离的倒数作为个体味道浓度判定值.
步骤 4.将味道浓度判定值代入适应度函数求得个体的适应度值.
步骤 5.确定具有最优适应度值的个体所在位置,以供其他个体借助视觉飞向此位置.
步骤 6.重复执行步骤2~5,直至迭代次数超限,结束算法.
上述基本的FOA 容易陷入局部最优解,对此本文对其进行改进.理论上,可以通过将每次迭代寻优过程中果蝇群体的初始位置随机“小范围”地置于另一新位置以及增大果蝇个体寻优范围的方式帮助寻优过程有效地跳出局部死循环.值得注意的是,这里的“小范围”需要保证经上一次迭代得到的最优个体位置在本次迭代个体寻优范围内,进而使本次迭代能够得到比上次更优的结果.最终,得到IFOA.
2.3 基于IFOA-KELM 的攻击信号重构算法
利用IFOA 先对KELM 中核函数参数σ和惩罚因子C两个参数的初始值进行优化,再进行KELM的训练.具体的IFOA-KELM 算法步骤如下:
步骤 1.初始化果蝇群体大小particlesize,FOA 最大迭代次数Max_num,两个果蝇群体位置X_axis=[X_axis1,X_axis2]和Y_axis=[Y_axis1,Y_axis2]以及最优适应度值Smellbest.
步骤 2.设定果蝇个体初始寻优半径为(r1,r2),并随机给定果蝇个体搜寻方向(2×Random −1)∈[−1,1)以确定个体接下来飞向的位置

其中,i表示第i组果蝇个体,由C群体中的一个个体和σ群体中的一个个体组成.(Xi1,Yi1)表示C群体中第i个个体的位置,(Xi2,Yi2)表示σ群体中第i个个体的位置,Random是一个 [0,1)范围服从均匀分布的随机数,i=1,2,···,particlesize.
步骤 3.计算第i组果蝇个体分别与 (0,0)之间的距离Di=[Di1,Di2],其中,

以及相应的味道浓度判定值Si=[Si1,Si2],其中,
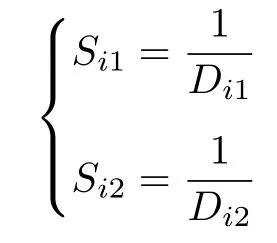
步骤 4.将味道浓度判定值Si代入如下适应度函数以得到适应度值Smelli
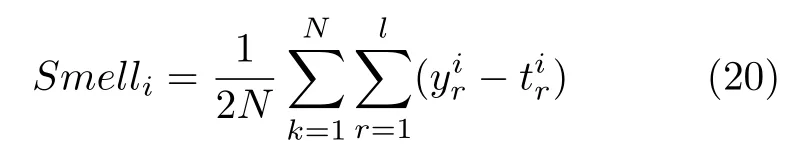
其中,N为训练样本数.
步骤 5.确定具有最优适应度值的果蝇个体组

其中,Smell=[Smell1,···,Smellparticlesize],best-Smell表示最优适应度值,bestIndex表示得到最优适应度值的果蝇个体组号.
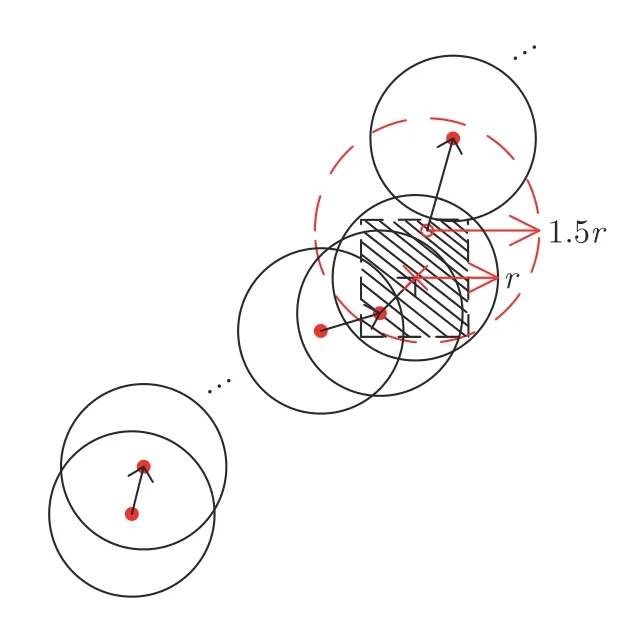
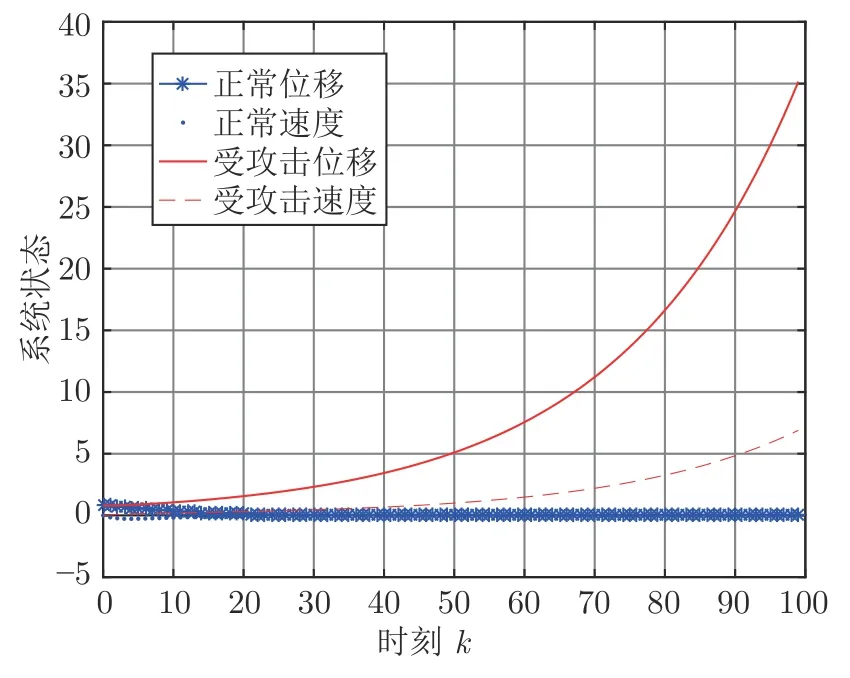
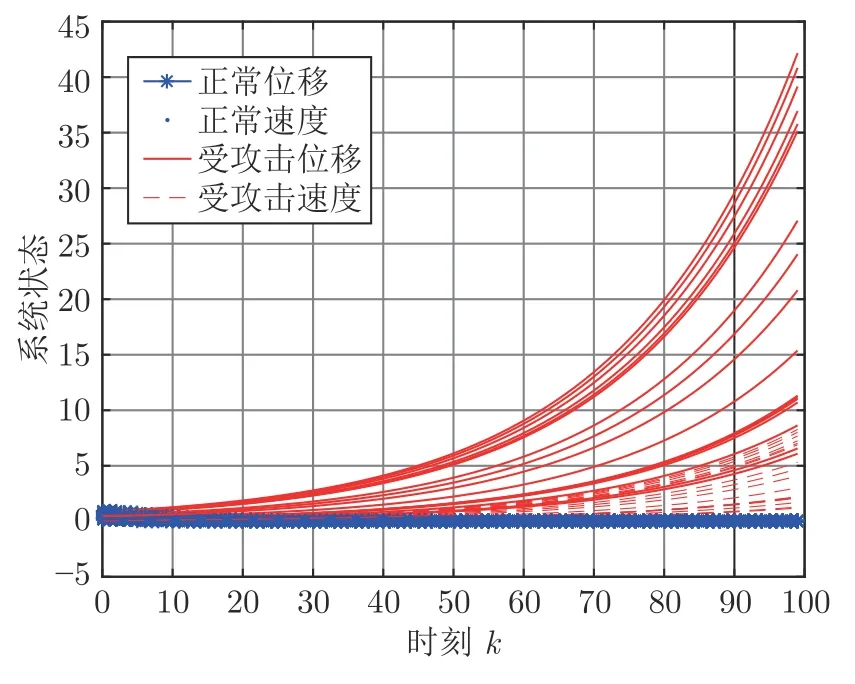
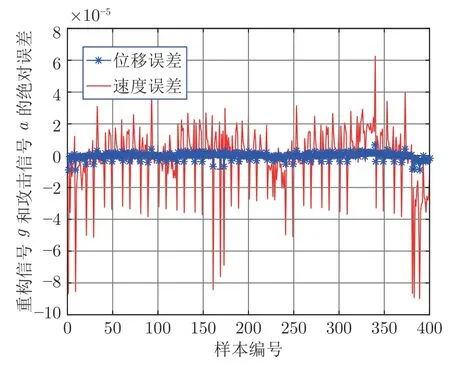
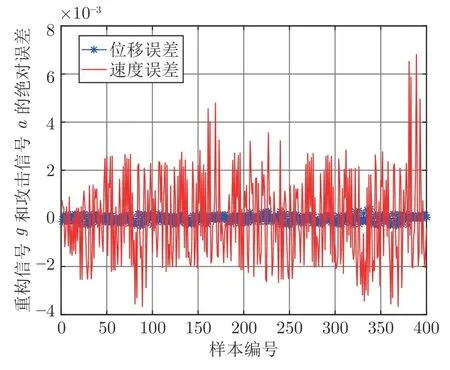
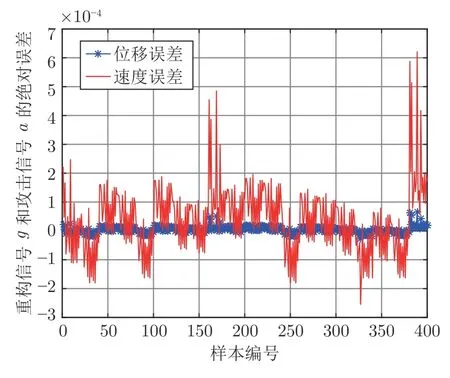
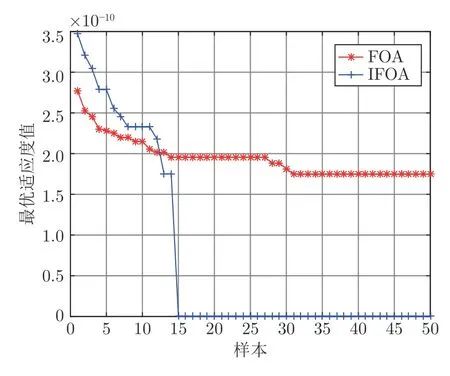
步骤 6.判断bestSmell 其中,Xi=[Xi1,Xi2],Yi=[Yi1,Yi2]. 否则,按照式(23)更新下次迭代的初始果蝇群体位置X_axis,Y_axis和果蝇个体寻优半径r 其中,r=[r1,r2]. 将本次迭代产生的最优个体位置作为下次迭代的初始果蝇群体位置,即满足X_axis=Xbest和Y_axis=Y best. 步骤 7.重复步骤2~6,为了防止KELM过拟合,需要满足Smellbest不超过给定值θ; 此外,当前迭代次数不得超过Max_num.否则,跳出循环,并将SS的最后记录用于训练KELM. 步骤 8.利用训练好的KELM 对需要测试的样本数据进行预测,算法结束. 注 2.由式(20)可知,适应度值实为KELM 算法的均方误差损失项,如果一味地追求训练集上误差损失最小化,则会导致所训练的算法过分拟合训练集,从而导致所训练算法在测试集上表现变差.所以,需要针对Smellbest给出合适的下界θ以防止IFOA-KELM 算法过拟合.这里合适的θ值需要通过反复试验来获取. 以单个果蝇群体为例,具体的IFOA 寻优过程如图4 所示.其中,“×”代表局部最优解,阴影区域表示最优位置坐标变化范围.由图4 可看出,当寻优过程陷入局部最优解时,会通过移动最优位置坐标以及放大搜索半径的方式设法跳出局部最优解. 图4 IFOA 寻优过程Fig.4 The optimization process of IFOA 基于上述IFOA-KELM 算法得到重构的攻击信号g(xc(k),Kxc(k)). 注 3.径向基函数g(xc(k),Kxc(k))满足Lipschitz条件. 将g(xc(k),Kxc(k))与真实攻击信号a(xc(k),Kxc(k))之间的偏差记为ω(k),由前馈神经网络的万能逼近特性[30]得 其中,γ >0 为偏差上界. 为保证受攻击系统的安全运行,将系统(2)的状态反馈控制策略更新为u(k),此时系统的状态方程可表示为 利用g(xc(k),Kxc(k))替代式(25)中的真实攻击信号a(xc(k),Kxc(k))得到标称模型 显然,f(x,u)满足Lipschitz 条件,并设f(x,u)关于x的Lipschitz 常数为Lf∈(0,∞). 由式(24)可知,f∗(xc(k),u(k))与f(xc(k),u(k))满足 因此,可将式(25)看作是包含有界外部扰动的不确定系统.由式(24)可知,所得受攻击系统的标称模型与真实受攻击系统模型之间存在一定的误差,此时如果继续使用状态反馈控制策略,仅仅改变控制律的状态反馈增益矩阵,不能够很好地应对该误差进而保证被控系统的稳定性.而MPC 具有良好的内在鲁棒性,并且可以结合合适的收缩约束条件很好地处理这一问题.因此,在得到式(26)之后,假设攻击者不再更新其攻击策略,使用MPC 策略对受攻击系统进行控制以保证系统安全运行. 模型预测控制是一种基于模型的开环最优控制策略[31−32],通过在线求解有限时域优化控制问题计算预测状态和未来的控制输入. 为了获取使得受攻击系统安全运行的控制信号u(k),本文求解如下有限时域MPC 优化问题 其中,决策变量uM(k+j|k)定义了模型预测控制器在k时刻预测的k+j时刻控制输入,因此UM(k)={uM(k|k),···,uM(k+Hp −1|k)}表示系统在未来预测时域Hp内的控制输入序列;xc(k+j|k)表示在UM(k)作用下标称系统k+j时刻的预测状态;Ω表示终端状态约束集.将优化问题(28)的最优解表示为,相应的预测状态为,其中=xc(k)=xc(k|k),与此相对应的最优成本记为.系统在k时刻的实际输入为uM(k)=.现将成本函数,UM(k))定义为 其中,L(x,u)为阶段成本函数,V(xc(k+Hp|k)为终端成本函数. 引理1[33].基于标称模型的最优预测状态与真实状态xc(k+j)(j≥1)之间的偏差满足以下关系 针对阶段成本函数及终端集,本文给出如下假设: 假设1.假设阶段成本函数L(x,u)满足L(0,0)=0 并且是Lipschitz 连续的,记L(x,u)相对x的Lipschitz 常数为Lc∈(0,∞);另外,存在常数φ>0 和σ≥1使得L(x,u)≥φ‖(x,u)‖σ成立,即 假设2.定义 Φ 是对于标称系统(26)的一个正不变集,且 Ω⊆Φ.存在局部控制器uM(k)=h(xc(k))以及相关Lyapunov 函数使得 1)对于xc(k)∈Φ,V(f(xc(k),h(xc(k))))−V(xc(k))≤−L(xc(k),h(xc(k))). 2)终端成本函数V(x,u)在 Φ 内是Lipschitz连续的,相对x的Lipschitz 常数记为Lv,即 其中,Φ={x∈Rn:V(x)≤α}. 假设3.集合 Ω={x∈Rn:V(x)≤αv}满足∀x∈Φ,f(x,h(x))∈Ω. 引理2[33].假设k时刻优化问题(28)存在最优解,据此构造k+1时刻的解,即 则由标称模型(26)得到的k+1 时刻预测状态序列为,其中=xc(k+1|k+1).此时,预测状态和的偏差满足 定理1.当闭环系统(25)的参数满足假设1~3 以及时,优化问题(28)是迭代可行的,并且闭环系统(25)是ISS 的. 证明. 1)可行性.由假设2 和引理2 得 2)稳定性.由假设1~3 以及引理1 和引理2 得 本节将通过数值算例验证本文提出的基于机器学习的安全控制策略的有效性.考虑如图5 所示的弹簧−质量−阻尼系统.其中,m表示物体的质量,u表示作用在物体上的力,s表示物体的位移,v表示物体的运动速度,Kl表示弹簧的弹性系数,Kd表示阻尼器的阻尼系数. 图5 弹簧−质量−阻尼系统结构图Fig.5 The structure of spring-quality-damping system 未受攻击的系统模型为 其中,x(k)=[sT(k),vT(k)]T. 假设攻击者按照设计的最优攻击策略(3)和(13)对系统(33)进行攻击,其中,Ba=I2.令Q=,R=1,由式(10)~(12)得到 将P11代入式(13)得到受攻击后的系统模型 设系统的初始状态为x0=[0.8,0]T,则系统在受到攻击前后的状态变化曲线如图6 所示.从图中可以看出,受攻击后的系统状态发散. 图6 系统状态轨迹Fig.6 The state of the system 通过随机选取16 组不同的初始状态生成如图7 所示的1 600 组数据 (xc(k),a(k)).将xc(k)作为输入样本,a(k)作为期望输出进行IFOA-KELM的训练,经IFOA 优化得到的KELM 初始化参数为Cbest=10 469,σbest=8.5945. 图7 训练样本Fig.7 The training sample 图8 IFOA-KELM 测试样本绝对误差Fig.8 The error between the real attack and the attack learned by IFOA-KELM 对比发现,IFOA-KELM 的学习效果要优于FOA-KELM、PSO-BP 和LS-SVM.因此,本文选用IFOA-KELM 对攻击信号进行重构,且γ=10−4. 为了对比IFOA-KELM 与FOA-KELM 的初始参数值优化性能,将IFOA 与FOA 同样迭代50次后得到二者的最优适应度值变化曲线,如图12所示. 由图12 可以看出,FOA-KELM 的初始参数优化过程容易陷入局部最优解,收敛速度更慢;而IFOA-KELM 的初始参数优化过程能够及时跳出局部最优解,继续寻找最优解,收敛速度更快.此外,经过实验发现,当Smellbest<10−11时,利用IFOA 得到的最优参数C和σ训练的KELM 会产生过拟合,因此IFOA-KELM 算法中的θ取10−11. 图9 FOA-KELM 测试样本绝对误差Fig.9 The error between the real attack and the attack learned by FOA-KELM 图10 PSO-BP 测试样本绝对误差Fig.10 The error between the real attack and the attack learned by PSO-BP 图11 LSSVM 测试样本绝对误差Fig.11 The error between the real attack and the attack learned by LSSVM 图12 IFOA 和FOA 最优适应度值变化曲线Fig.12 The Smellbest of IFOA and FOA 为了保证受攻击系统的安全性,将系统的控制方式改为MPC.系统标称模型(26)的Lipschitz 常数为Lf=1.0539.根据式(29),将MPC 的阶段成本函数取为L(x,u)=,其中=0.5I2,=0.1,则阶段成本函数L(x,u)的Lipschitz 常数为Lc=0.5;将终端成本函]数取为,其中,,并由此得到Lv=2.2839.选取α=0.3,αv=0.2,分别对应正不变集Φ={x∈Rn:V(x)≤0.3},终端状态约束集 Ω={x∈Rn:V(x)≤0.2}.当系统运行进入到终端域 Ω 时,采用局部状态反馈控制器uM(k)=h(xc(k))=[−2.9281−1.8531]xc(k).此时,条件成立.因此,根据定理1 可知,闭环系统是ISS 的.对受攻击后的系统分别使用原有控制策略和MPC 策略进行控制,系统的状态变化曲线如图13 所示. 图13 受攻击系统引入MPC 前后的状态轨迹Fig.13 The state trajectory of the attacked system with MPC and without MPC 在MPC 策略中,系统受到的真实攻击信号a(xc(k),Kxc(k))与经IFOA-KELM 重构的攻击信号g(xc(k),Kxc(k))之间的绝对误差如图14 所示. 图14 真实攻击信号与重构攻击信号之间的误差Fig.14 The error between the real attack and the learned 本文针对受攻击的信息物理系统设计了一种基于机器学习的安全控制方法.首先,提出了一种IFOA-KELM 算法对攻击信号进行重构.然后,对受攻击系统设计MPC 策略,并给出了使被控系统输入到状态稳定的条件.此外,从攻击者角度建立了优化模型,得到最优攻击策略以生成足够的受攻击数据.最后,利用以弹簧 − 质量 − 阻尼系统作为物理对象的CPS 进行数值仿真,将IFOA-KELM、FOA-KELM、LS-SVM 和PSO-BP 的攻击信号重构效果进行对比.仿真结果表明IFOA-KELM 的初始参数优化阶段能够有效解决FOA-KELM 初始参数优化阶段容易陷入局部最优的问题,加快整个寻优过程的收敛速度,并且IFOA-KELM 相较其他三种算法能够获得更好的拟合效果;此外,还验证了本文所提安全控制策略的有效性. 另外,本文所提的基于机器学习的攻击信号重构算法和MPC 算法均需要较大的计算资源.因此,本文接下来将考虑利用云计算实现上述算法,并进一步考虑云控制系统[34]的安全问题.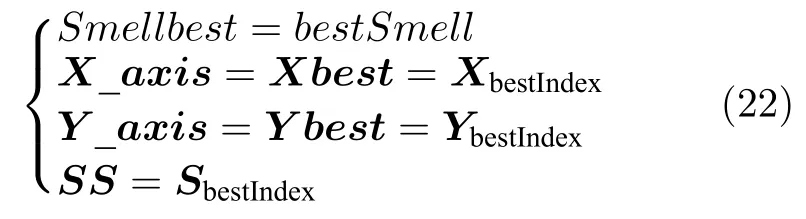

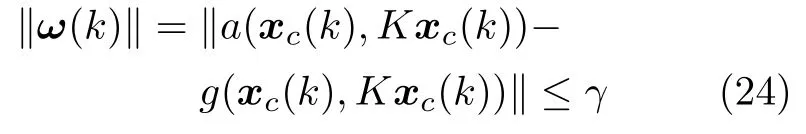



3 模型预测控制器
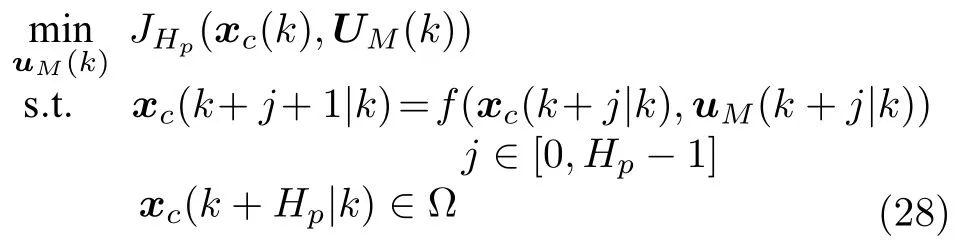
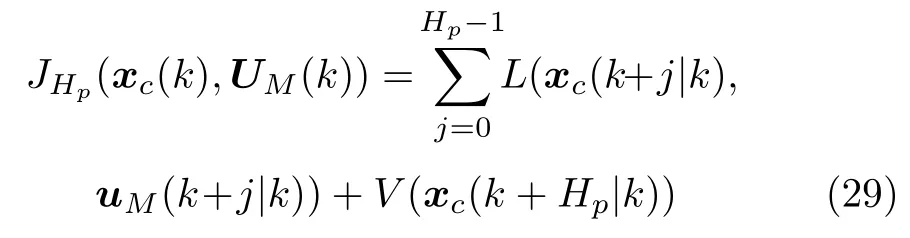

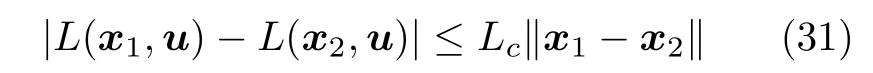



4 数值仿真及结果分析






5 结论
