基于非静压模型类海啸波作用下海堤越浪特性

屈 科，李凯伦，蒋昌波，邓 斌，刘铁威，蓝港芸

（1.长沙理工大学水利工程学院，湖南 长沙 410114；2.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114；3.洞庭湖水环境治理与生态修复湖南省重点实验室，湖南 长沙 410114）

海啸受灾程度与其越浪量密切相关，为研究海啸波的越浪特性，国内外的学者开展了大量的物理模型实验和数值模拟工作。通常认为孤立波与海啸的首波存在一定的水动力特性相似，因此，过去的许多学者常常采用孤立波作为海啸波模型，开展了大量的研究工作。Ozhan 等[1]通过物理模型实验，测量了不同入射波条件下陡斜坡海堤模型的越浪特性，并且采用堰流比拟方法提出了一种计算孤立波越浪量的经验公式。Geeraerts 等[2]基于Navier-Stokes 方程采用SKYLLA 方法模拟了波浪的越浪，结果表明在越浪量小的时候与实验值相差很大，而在越浪量大的时候较为符合。Hubbard 等[3]基于非线性浅水方程建立了OTT-2D 模型，模拟了沿不同角度传播的波浪的越浪过程，在模型中充分考虑了底部切应力的影响，计算结果与实验数据拟合较好，但某些工况下沿着不同方向入射波浪的越浪量不能很好地体现出来。Caroline[4]系统研究了群波、聚焦波以及孤立波作用下海堤的越浪特性，研究了入射波高与单宽越浪量之间的关系。Hsiao 等[5-6]针对孤立波在海堤上越浪过程的三种基本形态，进行了一系列的水槽实验，对孤立波传播变化过程、海堤波压、越浪量及最大爬高进行了测量与分析。Stansby[7]基于高阶Boussinesq 方程建立了孤立波爬高与越浪的数值模型，分析了不同入射波条件下孤立波爬高和越浪流层厚度的变化规律。曾婧扬等[8]采用两相流模型对斜坡堤的越浪特性进行了较为系统的数值模拟研究，给出了越堤流厚度和最大流速度的沿程变化特征。Yamamoto 等[9]基于海啸和风暴潮对海堤和护岸的破坏进行案例分析，并开展海堤越浪断面物理模型实验，提出了海啸波的平均越浪量公式。

前人开展波浪作用在海堤产生越浪的研究时，基本采用孤立波作为海啸波模型。然而，孤立波在周期、波形及水动力特性方面均与实测海啸波形存在较大差别。为了更好地模拟真实海啸波的水动力学特性，近10 a 来，一些特殊波形如：N 形波[10]，拉长的孤立波[11-12]和正弦波[13]等被用于研究真实海啸波的演变过程。Chan 和Liu[14]采用3 个双曲正割函数波叠加的方式来模拟2011 年日本海啸岩手南站实测的海啸波形。Qu 等[15-17]基于Chan 等[14]提出的叠加波形，采用参数化的方法系统研究了类海啸波和孤立波水动力特性对比[15]、类海啸波和水平圆柱相互作用[16]以及类海啸波作用下海堤堤后砂床形态变化[17]等。这些研究结果均表明，采用孤立波模拟真实海啸波存在较大的水动力学偏差。

笔者基于非静压单相流模型NHWAVE，采用Qu 等[15-17]提出的参数化类海啸波形，建立高精度数值波浪水槽，研究海啸波在斜坡海堤上越浪的水动力学过程，分析水深、波高、岸滩坡度及海堤坡度对海啸越浪量的影响，以期为近岸水利防护工程的建设提供参考。

1 数值模型

NHWAVE 非静压模型是一款开源程序，其求解的控制方程是基于σ 坐标系下的连续性方程和Navier-Stokes 方程，以及通过对湍流模型k-ε 求解获得计算值。采用了Godunov 有限体积法和有限差分法结合的混合格式，对控制方程组进行离散。本节对控制方程和湍流模型进行简要描述，关于数值计算模型NHWAVE 算法的详细描述参考文献[18]。

1.1 控制方程

NHWAVE 的控制方程为基于σ 坐标系的连续性方程和动量方程，其守恒形式的表达式为

式(1)—(2)中，t是时间，x、y、σ分别为笛卡尔坐标的三个方向，D为总水深。通量函数U、F、G、H分别为

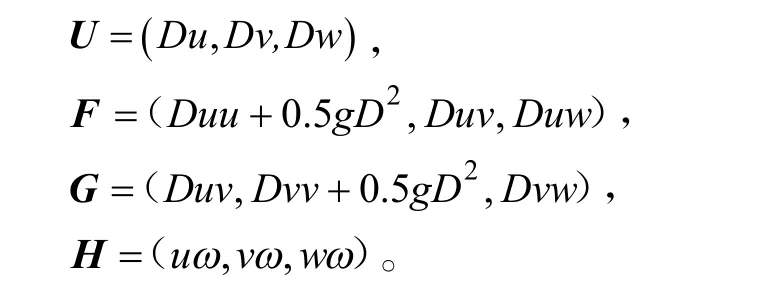
u、v、w分别代表x、y和z三个方向上的速度分量；ω代表σ坐标下的速度。Sh代表方程中的静压项，Sp代表方程中的动压项，Sτ代表湍流应力项；h是静止水深、p是压力、ρ是水密度，g为重力加速度。式（2）中各源项分别为

1.2 湍流模型

本研究采用标准的k-ε 湍流模型来计算湍流黏性系数，其控制方程为

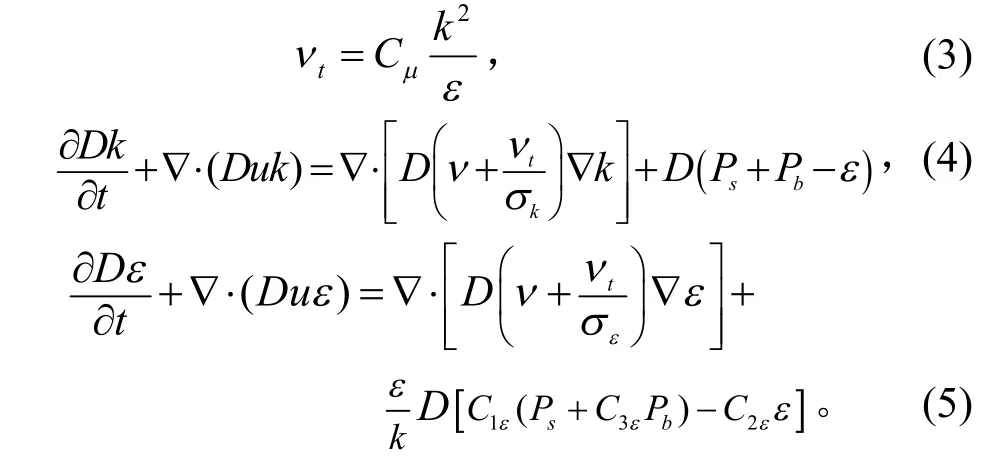
式(3)—(5)中，tν 为湍流运动黏度，σk、σε、C1ε、C2ε、C3ε、Cμ是湍流相关经验系数，其中σk=1.0，σε=1.3，C1ε=1.44，C2ε=1.92，C3ε=1.33，Cμ=0.09；k 是体积平均的湍流动能，；ε 是湍流耗散率，；l 为湍流长度尺度；Ps、Pb分别代表剪切力和浮力；∇为哈密顿算子。

2 模型验证

2.1 波形验证

本节数值计算了孤立波和类海啸波在水平区域的传播过程，并与解析解进行对比。为衡量孤立波与类海啸波的数值计算结果与实验结果、理论结果的吻合程度，引用R2进行评估，R2表示为

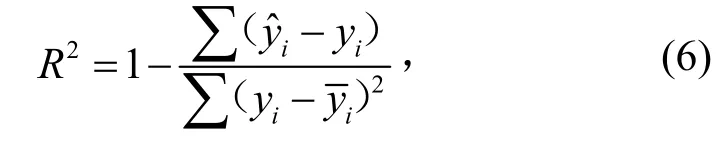
二维波浪水槽长度为20 m，波高H 和水深ℎ分别为0.1 m 和0.5 m。水平方向的网格大小dx=0.02 m，水深z 方向划分10 层网格，宽度y 方向采用1 层网格。时间步长 tΔ 采用自适应时间步长，满足Courant-Friedrichs-Lewy（CFL）条件，取CFL=0.1。图1_a 给出了不同时刻计算和理论孤立波水位线沿程分布的对比图。计算结果表明计算值与理论解吻合，NHWAVE 数值模型可以较好模拟孤立波的生成和传播过程。图1_b 显示了x=10 m 处计算得到的类海啸波形时程变化曲线与理论解的对比。经计算R2=0.99，该计算模型可以较准确地模拟类海啸波的演变过程。

图1 理论波型与数值计算结果的对比Fig.1 Comparisons of wave profiles between analytical solutions and numerical computation

2.2 孤立波与海堤相互作用

本研究采用Caroline[4]试验数据来验证NHWAVE模型模拟孤立波爬坡与海堤越浪过程，计算布置如图2 所示。计算区域总长度为30 m，斜坡坡度为1∶20，共布置5 个测针，位置分别为x=8.33、10.33、12.33、14.83、16.92 m。入射波高和水深分别为0.1 m 和0.5 m。水平方向的网格大小dx=0.02 m，水深z 方向划分10 层网格，宽度y 方向采用1 层网格。

图2 物理实验布置Fig.2 Layout for experiment work

孤立波与海堤相互作用大致可分为4 个过程：1）孤立波在斜坡上传播发生浅水变形，波高逐渐增大，波浪向前倾斜使波形呈不对称分布；2）孤立波产生浅水效应，前缘部分变得陡尖，形成一束斜上翘的水舌；3）孤立波到达海堤，水流越过海堤堤顶，发生越浪现象；4）破碎之后的波浪分为两股，一股形成反射流，另一股则继续沿斜坡爬升。

图3 就是t=9、10、11、13 s 时孤立波液面水位空间分布图，整个测量过程中数值计算值与实验测量值基本一致，说明数值模拟能够较准确地预测自由液面水位的空间分布。

图3 不同时刻自由液面沿程分布对比Fig.3 Comparisons of spatial distribution of water surface elevation at different time instances

图4 是不同测点处自由液面的时间序列图，经过计算，R2分别为0.91、0.87、0.85、0.90、0.98，R2均大于0.85，说明数值模型捕捉的自由液面随时间演变过程与物理实验值拟合较好。

图4 不同测点处自由液面时程变化曲线Fig.4 Time series of water surface elevation at different wave gauges

2.3 单宽越浪验证

本研究通过墙顶中间断面流速与越浪流厚度之积对时间求积分的方法求得某一时间段内的单宽越浪量，见式(7)：式中，v(t)是堤顶中间断面某时刻的越浪流平均流速，h(t)是中间断面越浪流在该时刻的越浪流厚度。

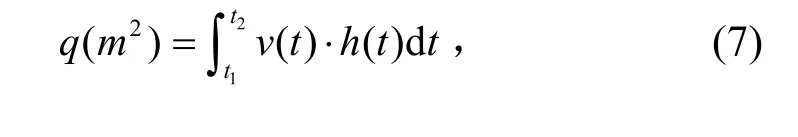
图5 给出了孤立波作用下海堤单宽越浪量随时间的变化趋势，海堤单宽越浪的数值计算值是30.7 L/m，实验测得的结果是30.07 L/m，误差仅为2.10%。综上所述，非静压模型NHWAVE 具备开展海啸波作用下海堤的越浪特性研究的能力。

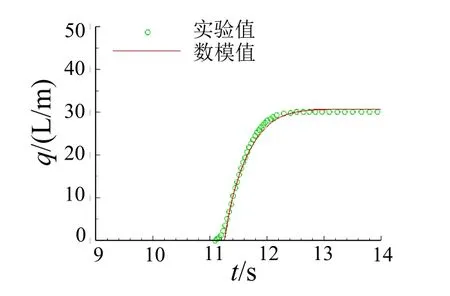
图5 单宽越浪量随时间变化Fig.5 Time series of overtopping water volume per unit width

3 水动力特性分析

本研究以Hubbard 等[3]在英国海岸研究实验室（UKCRF）进行的孤立波爬坡与越堤实验地形作为数值计算的标准地形，为了适应类海啸波波长的特点，适当延长造波边界与坡脚之间的距离（图6）。计算区域总长度设置为60 m，水平方向的网格大小dx=0.02 m，水深z 方向划分10 层网格，宽度y 方向采用1 层网格。初始岸滩坡度为1∶20，坡脚与造波边界的距离为38.33 m，其上布置了一个断面形状为等腰梯形的海堤，海堤顶部水平，两边坡度约为1∶2.178。沿着计算区域共布置16 个水位测点。其中WG1—WG4 位于深水区，用于测量入射及反射波高，WG5—WG7 布置在岸滩斜坡上，用于测量发生浅水变形的波高变化，WG10—WG12位于海堤前坡，用于测量越堤水体的波形历时，WG13—WG16 位于堤及堤后，用于测量波浪越堤的爬高。在标准计算地形的基础上，本文通过设计不同的计算工况，深入分析不同入射波高Hi、水深hi、岸滩坡度(1∶mi)及海堤坡度(1∶ni)等因素对类海啸波海堤越浪的影响，并与孤立波的计算结果进行对比。

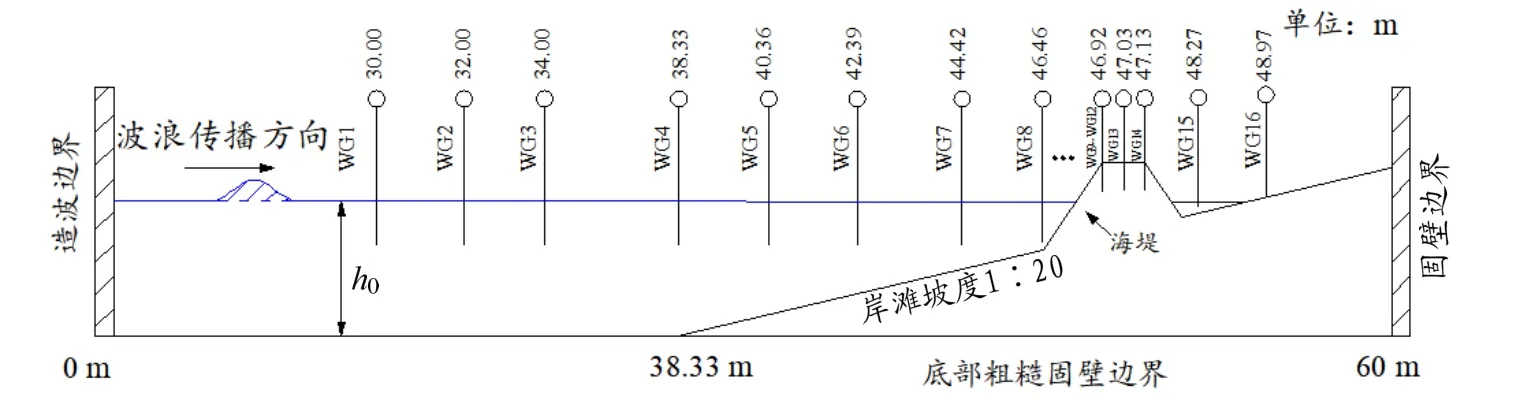
图6 计算区域布置Fig.6 Computational domain layout

本研究共设置20 种工况，类海啸波的标准工况为水深h0为0.5 m，波高H0为0.1 m，海滩坡度为1∶20，堤的坡度为1∶2.178，堤顶相对超高Rc/h0=0.235，具体工况如表1。

表1 数值模拟工况设置Table 1 Parameter setup for numerical runs

本节讨论标准计算工况（h0=0.5 m，H0=0.1 m，mi=20，ni=2.178）类海啸波与孤立波海堤越浪过程的水动力特性。图7 给出不同时刻类海啸波与孤立波水位沿程分布（类海啸波造波时间比孤立波长约32 s）。当波浪在深水区传播时，类海啸波与孤立波基本保持完整波形，与孤立波相比，类海啸波水面雍高较大（图7_a）；当波峰接近海堤时（图7_b），受到浅水作用的影响，类海啸波波形变化更为明显，波形更加陡尖。受到海堤的阻挡作用，类海啸波波面抬升更高；图7_d 所示孤立波的单宽越浪量（0.0237 m2）明显小于类海啸波的单宽越浪量（0.0509 m2）；越浪水体均沿着岸滩向上爬升，类海啸波越浪流厚度较孤立波更大（图7_e、图7_f）。

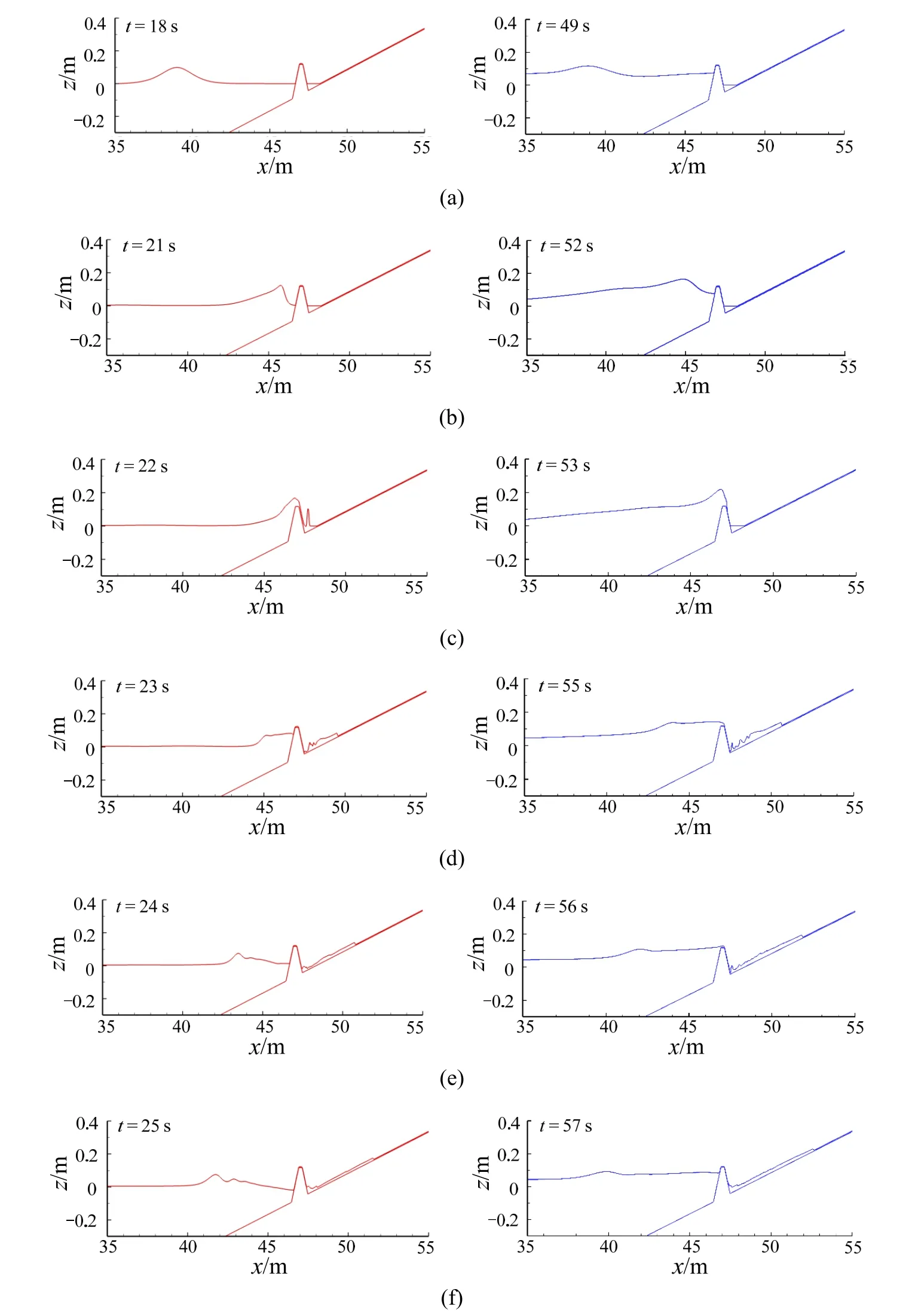
图7 不同时刻水位沿程分布Fig.7 Spatial distribution of water surface elevation at different time instances

图8 展示类海啸波和孤立波不同水位测点处的相对波高随入射波高的变化，其中Ht是测针处当地波高，Hi是入射波高，Hi/h0为相对入射波高，Ht/Hi为当地相对波高。测针WG1 处，孤立波和类海啸波保持完整波形，入射波高的变化对相对波高的影响不大。WG6 和WG7 位于岸滩斜坡上，波浪浅化较为明显，当地相对波高均有所增大，但孤立波的当地相对波高随入射波高的变化不明显，而类海啸波WG6 的当地相对波高在Hi/h0小于0.2 时持续增加，在Hi/h0=0.2 处达到最大值，而后波高继续增大使当地相对波高迅速降低，是因为类海啸波在此处前已开始破碎。而WG7 处显示类海啸波的当地相对波高随入射波高增加，是由于WG7 距离海墙较近而类海啸波空间尺度又较大，其前导波形撞击海墙后产生的反射回流将主波不断雍高所致。当孤立波与类海啸波传播到WG10 时完全破碎，使当地相对波高一直减小，至此不同入射波高下的当地相对波高均达到最大值，孤立波在Hi/h0=0.12 时达到最大值2.06，Hi/h0=0.28 时达到最小值1.20，而类海啸波的最大值为2.36，最小值为2.05，均大于其他位置测点处与之对应的相对波高。由于海墙的反射及能量的损耗，波高比会小于1，测针WG13 位于墙顶，WG16 位于海墙坡后，相对波高即代表越浪流水体的厚度，可以看出类海啸波水体厚度随波高比的增大而增大，而孤立波变化较小。

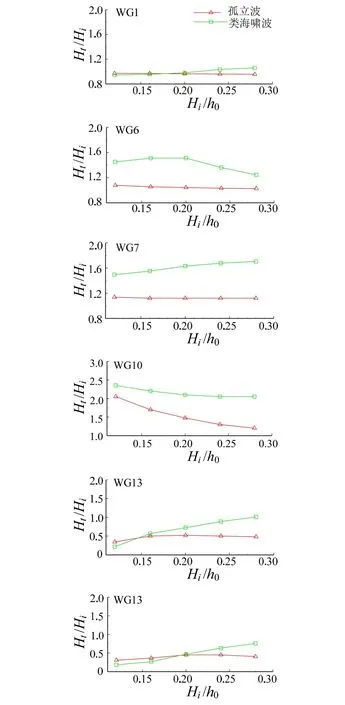
图8 不同入射波高条件下不同测点相对波高变化Fig.8 Variations of wave height ratio at different wave gauges under different incident wave height

图9 给出类海啸波和孤立波不同时刻的速度云图对比。引入有效势能概念，将有效势能为 99.8%总势能所对应的波长作为有效波长[19]。从图9_a 可知，类海啸波与孤立波波速的最大值均出现在波峰处，由于类海啸波的有效周期和有效波长都大于孤立波[16]，所以高速区（v >0.3 m/s）的分布较孤立波更广。在破碎波前缘水体即将跃上顶时（图9_b），类海啸波前缘水流速度明显大于孤立波，且分布范围也较孤立波大。图10 为类海啸波与孤立波的越堤爬坡过程，堤前水体分为两股，一股在墙后坡坡脚处形成顺时针涡流（图11），剧烈紊动的水体在此消耗大量入射波能，随后水体继续沿岸坡爬升；另一股则受到海墙反射形成反射流，孤立波爬坡水体速度虽略小于类海啸波，但反射流速度明显比类海啸波大。

图9 类海啸波（左）与孤立波（右）的速度云图对比Fig.9 Comparisons of velocity contour of water body between tsunami-like waves(left) and solitary waves(right)

图10 类海啸波（左）与孤立波（右）的越堤爬坡过程Fig.10 Snapshots of the overtopping processes of tsunami-like wave (left) and solitary wave (right)

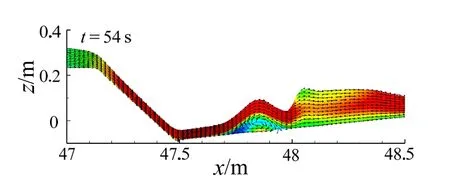
图11 堤后流线分布Fig.11 Distribution of streamline behind sea dike

图12 是孤立波与类海啸波的能量随时间变化曲线。其中能量的计算如式(8)—(10)所示：

式中，KE为动能；PE为势能；E 为总能；ρ 是水密度；u、w 为水平方向和水深方向的速度分量；z 为水深。

图12 中，孤立波（t=5 s）初始总能为159.1 J/m，类海啸波 (t=36 s) 初始总能为772.73 J/m。孤立波损耗总能约为80 J/m，类海啸波的能量损耗（166 J/m）明显高于孤立波，类海啸波和孤立波的能量损耗率分别为21.48%和50.28%。通过上述对比分析，孤立波与类海啸波的水动力特性存在明显的差异，采用孤立波作为海啸波模型研究海堤越浪特性存在明显不足。

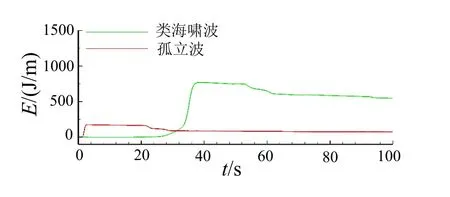
图12 孤立波和类海啸波波能量时程变化Fig.12 Comparisons of time series of wave energy between solitary wave and tsunami-like wave

4 不同因素对单宽越浪量的影响

本节分析孤立波和类海啸波作用下海堤单宽越浪量的变化规律。对于式（7）中时间t 的取值如下：t1=0 s，对于t2的取值应使越浪为一个波浪周期内的最大值，针对孤立波t2取50 s，类海啸波t2取82 s。由式（7）计算的单宽越浪量q（单位m2）将被用于后文的分析中。

4.1 水深的影响

本节针对不同水深下海啸波的单宽越浪进行研究。数值模拟选取波高H 为0.1 m，水深h 为0.35、0.40、0.45、0.50、0.55 m 五种工况，五种工况的其他因素与标准工况相同。

图13 给出4 种水深下类海啸波越过海堤时刻的速度云图。图13 可见，水深越浅时，破碎波浪撞击海堤时高速区的范围越大。水流前缘部分变薄，前部的速度保持最大。且随着水深的减小，海堤区域速度增大较为明显，最后形成一条斜向上弯曲的水舌。

图13 不同水深条件下类海啸波越堤速度云图Fig.13 Snapshots of velocity contour of water body of tsunami-like wave under different water depth

图14 给出的是单宽越浪量与水深的关系曲线，从图中五种工况中可以发现，图中的曲线均呈上升的趋势，随着水深的增加，越浪量相应增加，相对波高和相对堤顶超高都逐渐减小。孤立波的越浪量与海啸波有着很明显的区别，每种水深下海啸波的越浪量都要大于孤立波下的越浪量。差值随着水深的减小而减小，在水深为0.35 m 时差值趋于零，这是水深越小，堤顶的相对超高越大的原因。

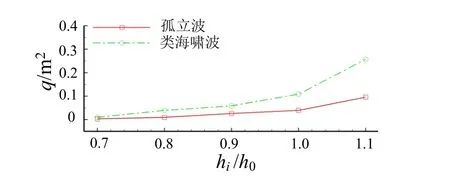
图14 单宽越浪量随水深的变化Fig.14 Variations of overtopping water volume with water depth

4.2 波高的影响

本节针对不同波高下海啸的越浪量进行研究。数值模拟选取了水深0.5 m，波高 0.06、0.08、0.10、0.12、0.14 m 这五种工况。相同的水深下，当海啸波的波高不同时，越浪量的差别较大。

图15 为不同波高下海啸波越堤时的速度云图，波高越大，水面雍高越明显，前缘部分水质点的速度越大，将产生更多越浪。

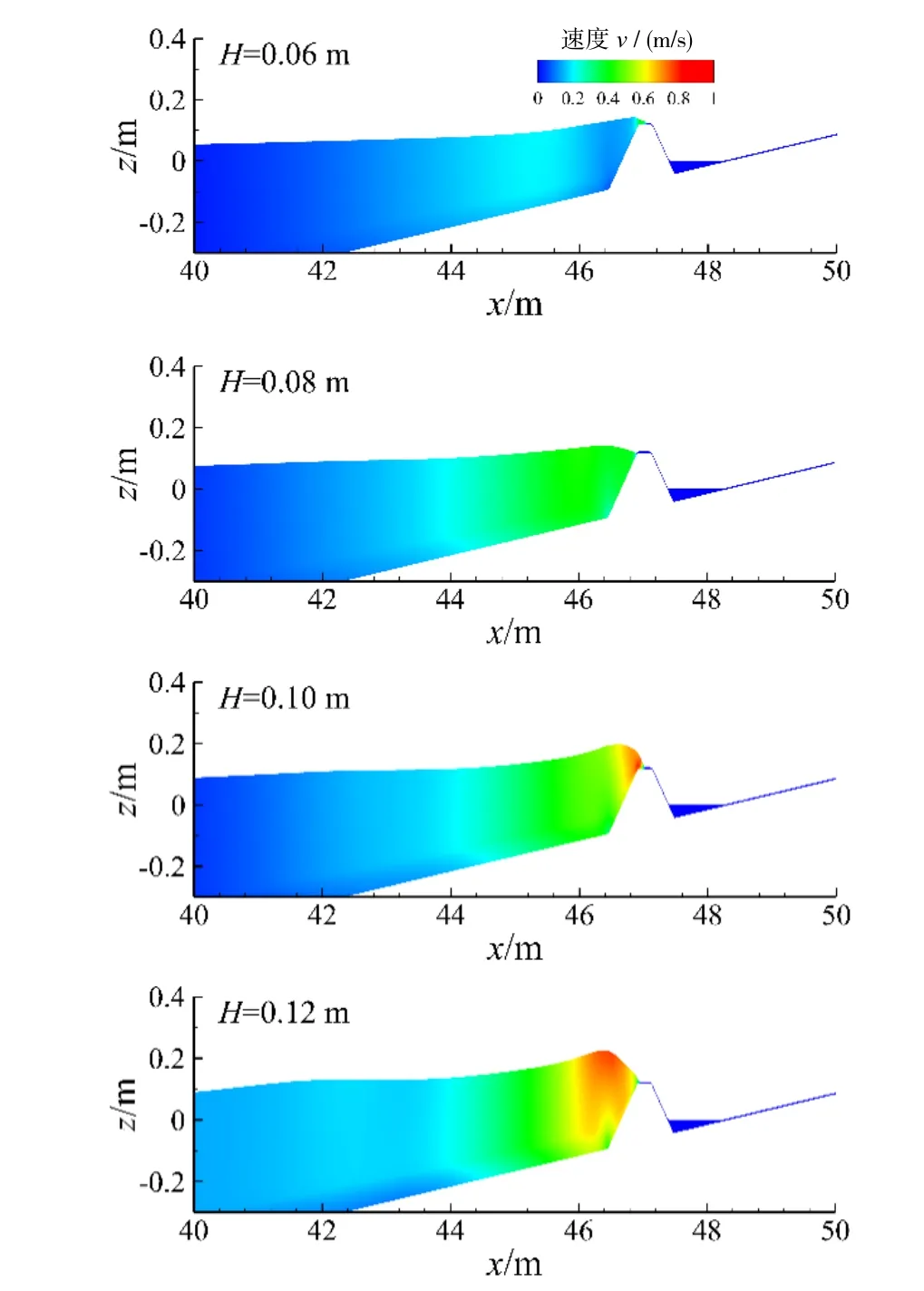
图15 不同波高下海啸波越堤速度云图Fig.15 Snapshots of velocity contour of water body under different wave heights

具体越浪的变化趋势如图16 所示，在0.5 m 的水深下，当波高等于0.06 m 时，海啸波翻越海堤后所产生的越浪量几乎为零，但随着波高的增长，越浪量快速增大。当波高小于0.1 m 时，越浪量与波高的规律与孤立波一样近似呈一次线性关系，当波高介于0.12 m 至0.14 m 时，越浪量的增长速度加快，当波高大于0.14 m 时，受到了堤顶相对高程的限制，造成一部分堤顶上的水体回流，导致增速减缓。总体而言，波高越大，一个波周期内所具有的能量及水量越多。

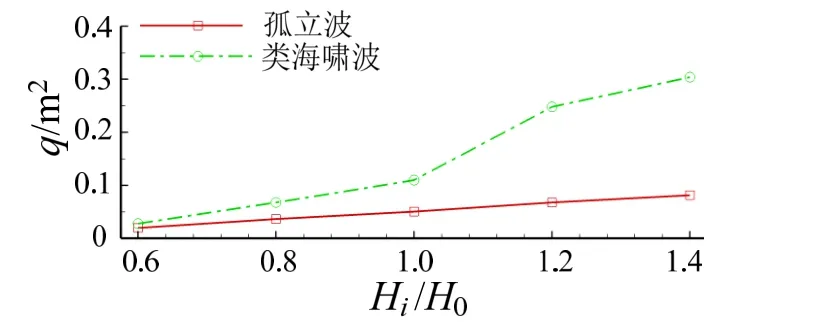
图16 越浪量随波高比的变化Fig.16 Variations of overtopping water volume with incident wave height ratio

4.3 海堤坡度的影响

本小节针对不同海堤坡度下海啸波越浪量进行研究。数值模型选择的海堤坡度为1∶1、1∶2.178、1∶3、1∶4、1∶5。

图17 为不同坡度的堤坡的横剖面图，堤顶水平并位于同一高程上，在x 方向的位置固定不变。

图17 不同堤坡下海堤位置的横剖面图Fig.17 Schematics of sea dike with different side slopes

图18 为不同堤坡下破碎波浪位于同一位置处的速度云图。堤坡由陡坡逐渐变缓时，破碎波浪的前缘部分接触海堤的时间会越来越早，图18_d 中的前缘部分就比图18_a、18_b、18_c 更早接触堤前坡。随着岸滩坡度的减缓，海堤对类海啸波前缘流速消减作用逐渐减弱，对比1∶1 两种坡度，明显海堤坡度为1∶5 时前缘流速更大，因此所耗散能量更多，更容易在此区域形成侵蚀作用，危害堤顶安全，实际工程中应采取相应措施对堤顶进行防护。

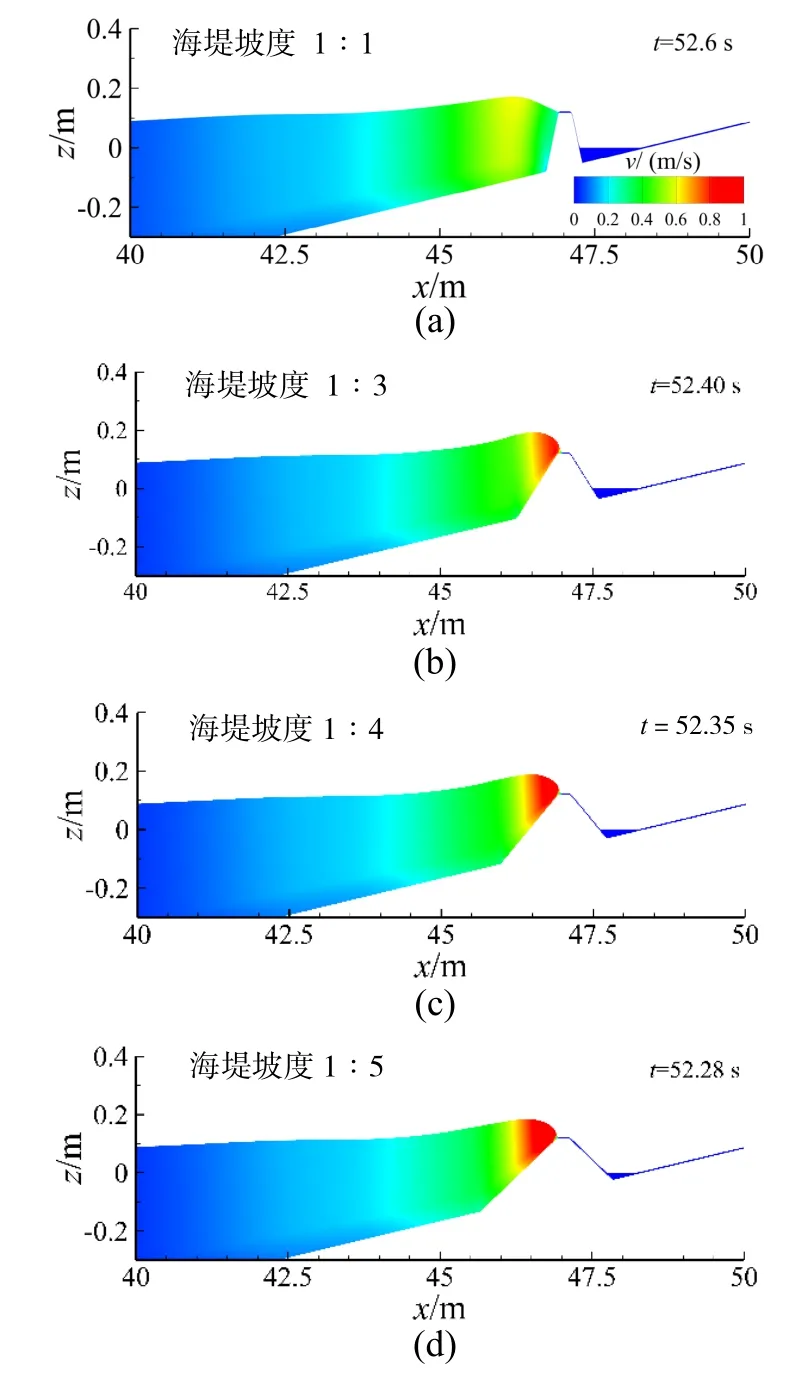
图18 不同海堤坡度下海啸波越堤速度云图Fig.18 Snapshots of velocity contour of water body of the sea dike with different side slopes under tsunami-like wave

在其他因素都相同的情况下，不同的海堤坡度对应着相同的相对堤顶超高，越浪量的具体变化如图19 所示，海堤坡度对于越浪的影响并没有波高与水深变化所产生的影响大。随着海堤坡度的逐渐变缓越浪量均缓慢呈线性增长，这是坡度越缓堤坡上的水体会越多的缘故，此时孤立波与海啸波的越浪表现出一致律。海啸波的越浪量是孤立波越浪量近2.4 倍。

图19 越浪量随海堤坡度的变化Fig.19 Variations of overtopping water volume with side slopes of sea dike

4.4 岸滩坡度的影响

本小节针对不同岸滩坡度下海啸波单宽越浪进行了研究。数值研究选择的岸滩坡度为1∶15、1∶20、1∶25、1∶30、1∶35。当改变岸滩斜坡的坡度时，不仅要保证海堤的位置固定不变，还要保证堤顶高程不变，即堤顶的相对超高Rc/h 不变。图20 为不同岸滩坡度的海堤纵剖面图。

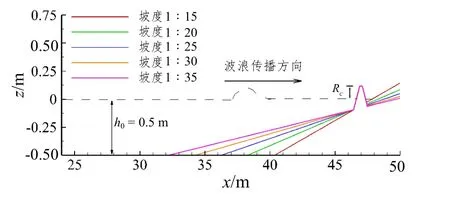
图20 不同岸滩坡度下海堤位置的纵剖面Fig.20 Schematics for sea dike with different beach slopes

图21 为类海啸波在不同岸滩坡度下即将越上堤顶并产生越浪时的速度云图。随着坡度减缓，波浪前端逐渐尖锐，速度在此处增加并聚集。图22所示，孤立波单宽越浪呈现出逐渐减小的规律。前述可知类海啸波经海堤相互作用后对能量的损耗率相对较小，使缓坡下的越浪量基本保持不变。对于陡坡的越浪，类海啸波的越浪量随坡度减缓而增加，且坡度为1∶20 时都达到了大值(q=0.111 m2)，这是因为在1∶20 坡度下，斜坡上的水体更多，能量的分布比1∶15 的坡度更广。

图21 不同海堤坡度下海啸波越堤瞬态速度云图对比Fig.21 Snapshots of velocity contour of water body under different slopes of sea dike

图22 越浪量随岸滩坡度的变化Fig.22 Variations of overtopping water volume with beach slope

5 结论

本研究基于非静压模型NHWAVE 建立高精度二维数值波浪水槽，通过对日本2011 年实测真实海啸进行参数化形成类海啸波形，并设置系列计算工况对类海啸波与海堤相互作用的复杂水动力特性进行了系统研究。重点讨论了类海啸波与孤立波在传播过程中的水动力差异以及在不同因素影响下海堤单宽越浪的变化规律。得出如下结论：

1）类海啸波有效波长大于孤立波，在不同位置处所引起的水面变化持续时间相比孤立波更长；

2）随波高和水深的增加，类海啸波和孤立波的越浪量均增大，且类海啸波越浪量大于孤立波；

3）海堤坡度越陡，海堤对波浪流速的消减作用越明显，但海堤坡度对越浪量的影响不大；

4）随岸滩坡度减缓，类海啸波的波浪速度将在堤前聚集，在1∶20 的岸滩坡度下越浪量达到最大，在工程实际中应避免此种地形坡度。