基于混合工质的多级蒸发ORC理论极限性能研究
2021-07-24曹健冯新吉晓燕陆小华
曹健,冯新,吉晓燕,陆小华
(1 南京工业大学材料化学工程国家重点实验室,江苏南京210009; 2 吕勒奥工业大学能源工程系,瑞典吕勒奥97187)
引 言
区别于传统蒸汽动力循环以水为循环工质,有机朗肯循环(ORC)采用低沸点有机物以降低蒸发温度,从而实现低温余热(低于473.15 K)的热功转换[1-2]。作为低温余热发电的首选方案[3],近年来,ORC 得到广泛的工业应用[4-7],但其循环性能仍不尽如人意,因此混合工质及工艺优化等改进策略相继被提出[8-11]。
混合工质在蒸发或冷凝过程中发生非等温相变,产生的温度滑移能够降低冷热源的传热温差以减少ORC 系统的有效能损失[12]。混合工质ORC(BZORC)的研究尚处于起步阶段[13],主要围绕工质筛选及配比、系统参数优化、经济性分析等方面[14-20]。近年来,一些研究表明,结合混合工质的特性进行ORC 工艺优化,取得了较可观的研究成果。Collings等[21]利用精馏塔调控混合工质组分以适应环境温度变化,以不到7%的投资成本增幅提高了ORC 系统23%的热效率。陈超男等[22]基于混合工质改进分液冷凝系统,较传统系统经济性可提高38.9%。
循环工质的蒸发过程是造成ORC 系统不可逆损失的主要因素[23],因此结合混合工质对蒸发过程的改进在提高系统循环性能方面具有极大潜力。Sadeghi 等[24]提出一种基于混合工质的两级蒸发ORC(DZORC),利用混合工质相对挥发度差异,通过部分汽化实现组分调控,以匹配不同温度区间的热源,研究结果表明:其系统净输出功较基本ORC(BORC)提高42.8%。Li 等[25-26]分析了热源温度和混合工质配比对DZORC的影响,从分析的角度评价了DZORC 的不可逆损失分布,以一定设计工况为例,MZORC 系统输出功及效率最高能获得25.6%的增幅。但是目前国内外关于DZORC的研究较少,并且仅限于两级,更多级蒸发对系统循环性能的影响仍未知,主要原因在于缺乏对改进蒸发过程所能达到的ORC 热力学极限的认识,从而无法准确判断DZORC 是否已经逼近热力学极限,有无增加更多蒸发级的必要。
因此,本文提出基于混合工质的多级蒸发ORC(MZORC)概念,并通过以环境温度T0为基准态的分析,建立MZORC 蒸发过程的传热极限模型。以热源423.15 K、环境温度298.15 K 工况为例,采用Aspen Plus流程模拟软件对BORC 及不同蒸发级数MZORC 进行设计及优化,结合传热极限模型研究系统循环性能的理论极限,并将其作为评价基准以对比BORC 与不同蒸发级数MZORC 的循环性能差异。
1 MZORC系统描述及原理
相较于BZORC 的一个蒸发器,MZORC 具有多个蒸发单元,混合工质在与低温热源逆流换热的过程中发生部分汽化,产生的不同压力蒸气分别抽提至透平完成发电。如图1 所示,每个蒸发单元由一个泵和蒸发器组成,MZORC 由n个蒸发单元构成,当n= 1 或n= 2 时分别变为BZORC 和DZORC。值得一提的是,根据蒸发器的布置DZORC可以分为串联型(STORC)和并联型(PTORC)两种[23],而本文提出的MZORC 是基于系统性能更优异的STORC 提出的。
MZORC包含工质泵、蒸发器、透平机、发电机和冷凝器五个组件,混合工质在各处均处于亚临界状态。图2 所示为MZORC 的T-s图,各点标注与图1相对应。在第一个蒸发单元中,混合工质经过低压工质泵1加压输送至低压蒸发器1(Ⅱ→1),通过与低温热源的热交换,混合工质发生部分汽化(1→1'/1″),产生的过热蒸气抽提至透平,蒸气膨胀做功,驱动发电机完成发电(1'→I)。
各蒸发单元的原理与上述第一个蒸发单元原理一致,只是在最后一个蒸发单元中,混合工质全部汽化产生高压蒸气n',与各蒸发单元产生的不同压力蒸气进入多级汽轮机的不同压力气缸,发生不可逆绝热膨胀(n'→Ⅰ),通过轴连器同速驱动透平机转子转动[27]。不同压力蒸气在多级汽轮机出口汇集,组分配比恢复初始状态。为防止损坏透平机,透平机出口蒸气通常为过热蒸气,通过冷却水冷凝为饱和液体(Ⅰ→Ⅱ),完成系统循环。
自过增元等[28]提出这一全新物理量描述物体传递热量能力以来,分析被广泛应用于评价传热过程的效率[29]。流耗散率Gdiss可以表示换热过程中的不可逆损失,定义为:
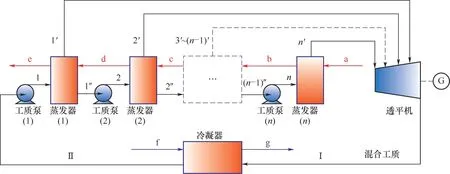
图1 MZORC原理Fig.1 Schematic diagram of MZORC

图2 MZORC系统T-s图Fig.2 T-s diagram of MZORC

式中,ΔGh代表热源在换热过程中给换热器带来的变,MW·K;ΔGc代表冷端通过换热过程得到的,MW·K。分别定义为:

式中,Q代表换热器的热负荷,MW;ΔTc和ΔTh分别代表冷、热源流体的温度变化,K。
MZORC 系统换热过程的温度与换热量之间的关系如图3所示。红色及蓝色曲线分别代表热源及混合工质的换热曲线。与图1 所示热源换热过程(a→e)不同的是,热源的换热曲线还额外增加了降温至环境温度T0部分。低品位热源可供回收热量较少,出口温度通常较低,基本无进一步回收利用价值,因此这部分热源出口携带的有效能将全部损失。为准确评价低品位热源在换热过程存在的所有不可逆损失,该换热过程模型将环境温度T0作为基准。在T-Q图中,热源及循环工质的变可以表示为换热曲线与T=T0基准线所围成的面积。流耗散率则表示为热源换热曲线与循环工质换热曲线围成面积之差,对应于图3 中的灰色阴影部分(包括灰底网格阴影部分)。
如图3 所示,混合工质的换热曲线可以根据蒸发级数划分为n段,每一段蒸发级内混合工质换热曲线又可分为两段。以第一蒸发单元为例,自T1升温至Teva,1段代表混合工质从过冷液相升温至饱和液相过程中的显热部分。自Teva,1升温至T1'段代表饱和液相部分蒸发至饱和气相的潜热部分。值得一提的是,对于纯工质而言,蒸发过程属于等温相变过程(蓝色虚线),而混合工质在蒸发过程存在一定温度滑移。热源及循环工质换热曲线的斜率可以表示为流体热容流率CP的倒数:

为简化换热过程模型的计算,本文做出如下理想化假设:(1)混合工质T随Q的变化呈理想线性关系;(2)混合工质在显热段和潜热段的热容流率CPs和CPp分别取流体的平均热容流率,并忽略不同蒸发单元中流体热容流率的变化;(3)热源的热容流率CPh、换热器夹点温差ΔTpp均为定值;(4)仅考虑有机混合工质的常见物性状态,满足CPs≤CPh和CPp≥CPh。

图3 MZORC系统的T-Q图Fig.3 T-Q diagram of MZORC
需要指出的是,利用工质泵改变循环工质进入蒸发器时的压力,可以调节MZORC 各蒸发单元的蒸发温度。在不同的CPs和CPp下,蒸发温度能够在某处使得系统流耗散率最低,此时的蒸发温度为系统最佳工况。冷凝过程中混合工质的温度滑移更加显著,通常表现为夹点位置处于冷凝器冷端,因此在一定环境温度T0及冷凝器夹点温差时,冷凝器出口混合工质温度即Tm,in为定值。本文将热源进口温度Th,in与循环工质进口温度Tm,in之差定义为ΔT,取各级蒸发温度为ΔT的等分点。如图3 所示,对于n级蒸发ORC 而言,各级蒸发单元的蒸发温度差为ΔT/(n+1)。在此理想化假设条件下,第一蒸发单元显热段和潜热段的系统热负荷Qs和Qp分别表示为:
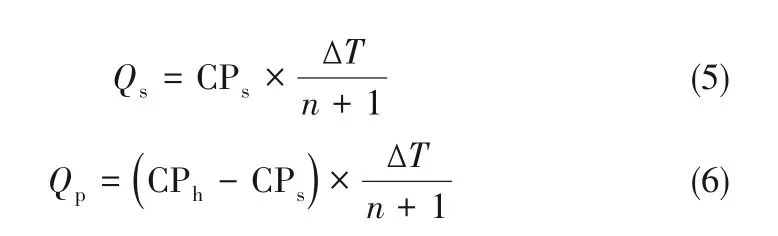
则MZORC 系统第一蒸发单元热负荷Qeva,1可以表示为:
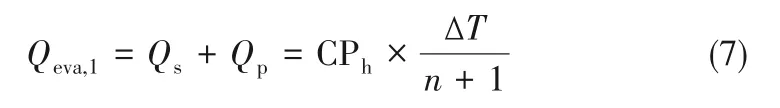
MZORC系统余热回收总量Qeva可以表示为:

式中,Qloss,es和Qloss,ex分别定义为必要热损失和额外热损失。由于考虑到循环工质进口温度(即循环工质在冷凝器出口处温度)与冷凝器存在一定传热温差,与蒸发器的夹点温差导致循环系统存在Qloss,es。由于循环工质与热源换热曲线无法完全实现以最小传热温差的距离完全平行,势必会产生Qloss,ex。两者分别表示为:


可知,Qloss,es的表达式中蒸发器夹点温差、循环工质进口温度和环境温度均为定值,因此Qloss,es为定值。而Qloss,ex与混合工质物性和MZORC 系统蒸发级数有关,CPs越大越有利于系统对于热源热量的回收。蒸发级数越多,系统造成的额外热损失越小,并且当蒸发级数无穷大时,系统额外热损失趋近于0,即以系统余热回收量表达的传热极限可以表示为:

对热损失的评价仅能体现系统余热回收的“量”,对余热回收的“质”的评价采用分析。与热损失类似,引入必要流耗散率Gdiss,es和额外流耗散率Gdiss,ex。根据式(1)~式(3),如图3 所示,灰底网格阴影部分的面积代表Gdiss,es,其他灰色阴影面积代表Gdiss,ex,表达式分别为:
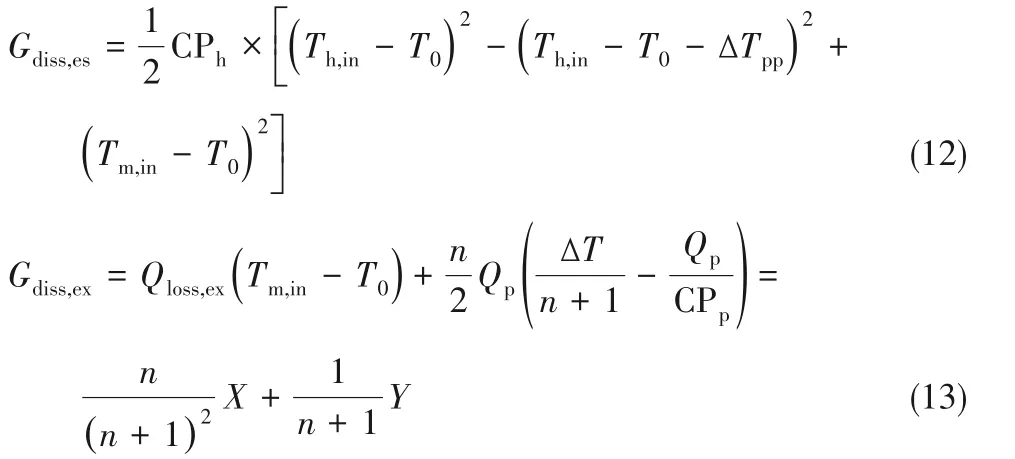
式中,X和Y分别为:
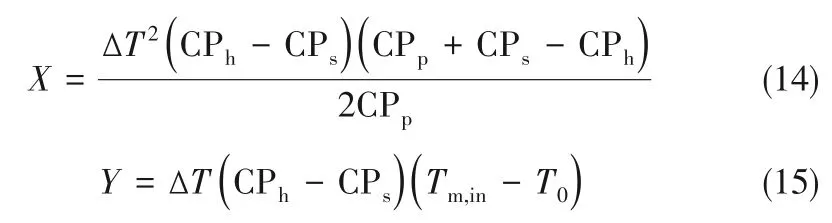
在工况保持不变的情况下,Gdiss,es、X和Y均为定值。由式(12)可知,系统蒸发级数越大,Gdiss,ex越小。当蒸发级数无穷大时,Gdiss,ex将趋于0,此时以系统总流耗散率表达的传热极限可以表示为:

根据式(11)和式(16)两种系统传热极限模型表达形式,系统传热极限仅与热源、环境温度工况条件及所设定的换热器夹点温差有关,不随循环工质、蒸发级数的变化而改变。定工况下,提高蒸发级数是实现系统蒸发过程逼近传热极限的有效策略,但势必也会增加系统投资成本,基于传热极限的评价相对不够直观。结合Aspen Plus 过程模拟能够建立理论极限性能与传热极限的对应关系,通过理论极限性能为基准的评价手段能够直观了解到更多级蒸发对系统循环性能的影响。
3 结果及讨论
本文以热源423.15 K、环境温度298.15 K 工况为例,对比BORC、DZORC 及基于混合工质的三级蒸发ORC(TZORC),以验证MZORC 系统的循环性能。采用Aspen Plus (V11)软件建立TZORC 流程模型如图4 所示,选用REFPROP 全局物性方法,流程模拟的工艺条件如表1[30]所示,R245fa/R134a 为此冷热源工况下的优选混合工质[31]。
采用Aspen Plus 的设计规定(Design Specs)及平衡模块(Balance)对TZORC 系统进行设计及优化。冷凝器出口温度为混合工质的饱和液相温度,对冷凝器夹点温差进行设计规定,从而确定混合工质R245fa/R134a的组分浓度。对蒸发单元采用能量平衡模块进行计算达到设定热源出口温度时的工质流量。对于TZORC 系统各蒸发单元的蒸发温度通过工质泵进行调节,以实现各蒸发器夹点温差符合表1 的设定值。以系统净输出功为优化目标,对热源出口温度进行优化,在最佳热源出口温度情况下进行不同蒸发器的汽化率的优化。

表1 流程模拟参数Table 1 Key parameters of process simulation
DZORC 系统的优化策略与上述TZORC 优化原理一致,BORC 的优化借鉴实际工业应用设计方式[32],分别对R245fa、R134a 为纯工质的ORC 进行优化设计。值得一提的是,TZORC 及DZORC 最后一级蒸发器汽化率均为1,因此DZORC 可以直接优化第一蒸发器汽化率,而对于TZORC 两个蒸发器汽化率的同时优化可以通过对各级蒸气摩尔配比的优化来实现。

图4 TZORC的Aspen Plus模拟流程Fig.4 Aspen Plus flowchart of TZORC

表2 MZORC与BORC循环性能对比Table 2 Cycle performance comparison between MZORC and BORC
为得到以系统净输出功表达的理论极限性能,将Wnet与Gdiss进行线性拟合如图5所示,可以发现Wnet与Gdiss基本呈线性负相关关系,并且满足一次线性回归方程y=3.79991-0.00105x。当MZORC 蒸发级数无穷大时,Gdiss,ex趋近于0,即Gdiss等于349.15 MW·K时,系统净输出功理论极限值为3.43MW。BORC、DZORC 及TZORC 的系统净输出功分别能够达到理论极限值的65.0%、79.0%及90.1%。因此,由以上分析可知,无论是工业化的BORC 还是目前研究前沿的DZORC 均还有改进优化的潜力,TZORC 或者是更多蒸发级数的MZORC 具有更优的循环性能,有望得到更进一步的研究及应用。
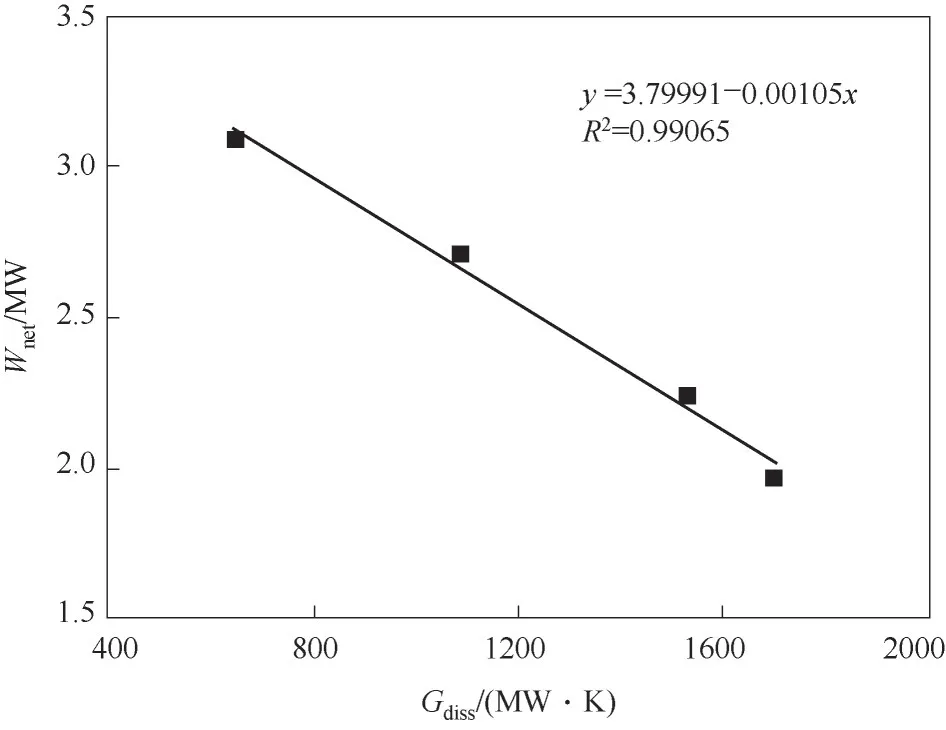
图5 Wnet与Gdiss的线性拟合Fig.5 Linear fitting of Wnet and Gdiss
4 结 论
(1)MZORC 能够通过降低循环工质蒸发过程带来的热量损失及流耗散率,从而提高系统循环性能,提高蒸发级数是实现系统蒸发过程逼近传热极限的有效策略。
(2)以环境温度T0为基准态的分析可以准确计算Gdiss,并且Wnet与Gdiss呈线性负相关关系。通过线性拟合可以外推得到Gdiss,es所对应的Wnet,即传热极限条件下系统的理论极限性能。
(3)在本文工况条件下,三级蒸发MZORC 系统净输出功较BORC 能够提升38.6%。BORC、两级蒸发和三级蒸发MZORC 的系统净输出功分别能够达到理论极限值的65.0%、79.0%及90.1%。目前研究前沿的DZORC较理论极限差距显著,在蒸发级数的优化方面仍具有较大潜力。
符 号 说 明
CP——热容流率,MW/K
Gdiss——流耗散率,MW·K
ΔG——变,MW·K
n——MZORC系统蒸发单元的数量
Q——热量,MW
T——温度,K
T0——环境温度,K
ΔTpp——夹点温差,K
W——功率,MW
下角标
c——冷端
es——必要值
eva——蒸发器
ex——额外值
h——热源
in——进口端
loss——损失
m——循环工质
net——净输出功
out——出口端
p——循环工质潜热段
s——循环工质显热段
