关于正定矩阵的Sz´asz 不等式和Hadamard 不等式的注记

刘合国, 高睿, 徐行忠, 廖军

(湖北大学数学与统计学学院, 湖北 武汉 430062)

1 引言

本文涉及的矩阵不等式见文献[1-2], 算术- 几何平均不等式(也称AM-GM 不等式) 见文献[3], 涉及的矩阵论知识见文献[4].

1893 年, Hadamard 证明了下面的定理, 它应该是行列式不等式里最有名的结果之一.

Hadamard 不等式设H=(aij)n×n是复数域上的n阶矩阵, 则

中“=” 成立当且仅当H是对角矩阵.

明显的, 上述不等式等价于下面的定理:

设A=(aij)n×n是正定Hermite 矩阵, 则中“=” 成立当且仅当A是对角矩阵.

人们常常把这个关于正定矩阵的不等式称为Hadamard 不等式, 例如文献[1-2]. 随后, Sz´asz 推广了Hadamard 不等式, 得到了一个加细的不等式, 见文献[1-2,4].

Sz´asz 不等式设A= (aij)n×n是非对角的正定Hermite 矩阵,Pk表示A的所有k级主子式的乘积(1 ≤k≤n), 则

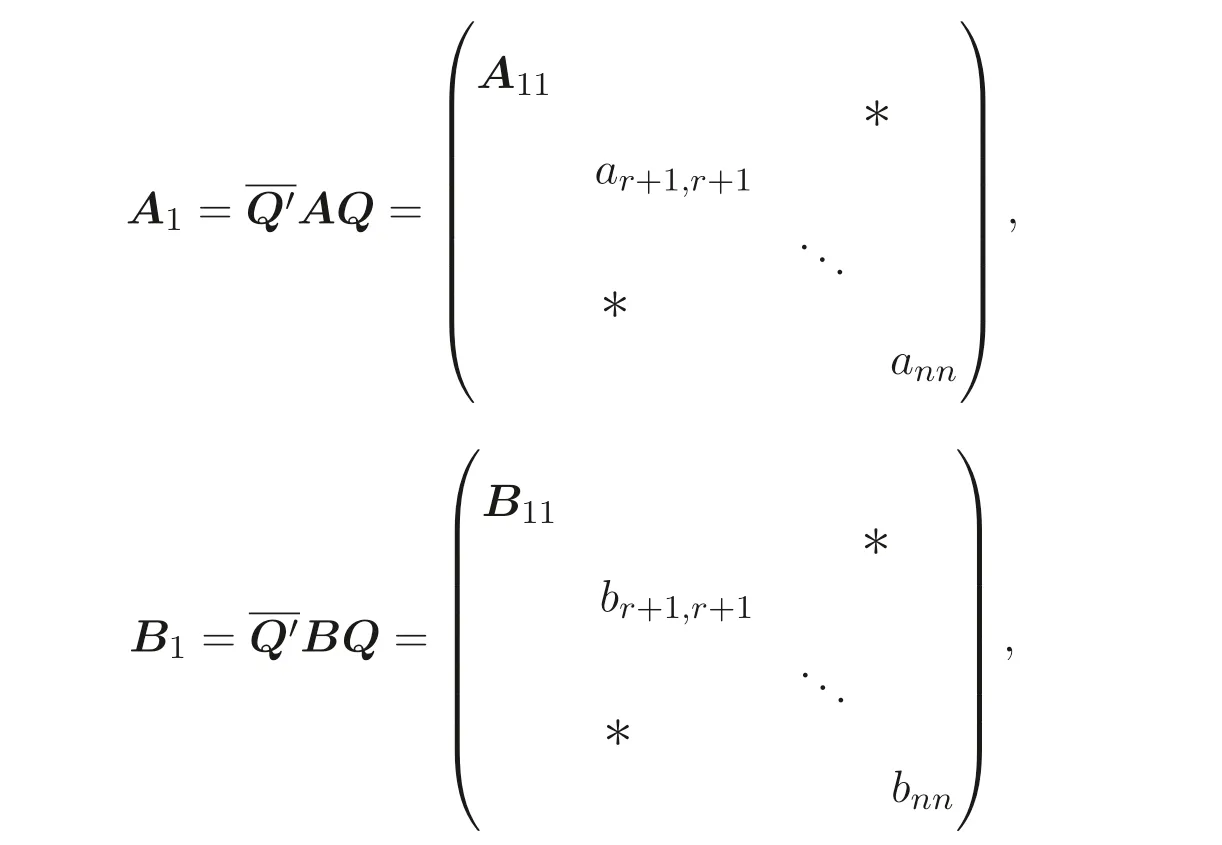
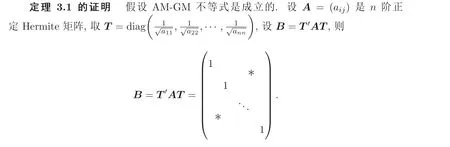
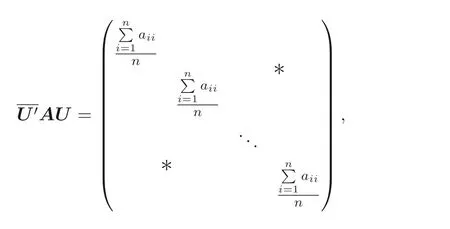
显然, Sz´asz 不等式里“Pn

本文包括两方面的内容, 它们在形式上看是相互独立的, 但在本质上是一脉相承的.其一, 给出Sz´asz 不等式的加法形式; 其二, 证明Hadamard 不等式等价于AM-GM 不等式. 贯穿全文的基本思想是“平均”. 有关Sz´asz 不等式的研究请参见文献[6-11], 关于Hadamard 不等式和平均值不等式可参见文献[12-15].

2 Sz´asz 不等式的加法形式

这个定理的证明依赖于两个已有的事实.

引理2.1把A= (aij)n×n的所有k级主子式之和记为Qk, 1 ≤k≤n, 则A的特征多项式

下面用微积分的技术给出该引理的一个简洁证明.

证明对n进行归纳. 当n= 1,2 时, 结论是易见的. 归纳地假设n −1 时结论成立, 注意到ΔA(λ) 的导数

的展开式的λn−k−1的系数里出现n −k次, 于是

令λ=0, 可得C=(−1)nQn, 因此

引理得证.

引理2.2(Newton-Maclaurin 不等式) 设λ1,λ2,··· ,λn是n个正数,σk是λ1,λ2,··· ,λn上的第k次初等对称函数, 1 ≤k≤n, 则有

并且上式里任意一个等号成立当且仅当λ1=λ2=···=λn.

这不是一个平凡的结论, 证明它需要有关“对称和” 形式的不等式的深刻技巧, 见文献[3] 中Problem 12.1.

有了这两个引理, 证明定理2.1 就是常规的工作了.

定理2.1 的证明设A的特征值为λ1,λ2,··· ,λn, 从条件知λ1,λ2,··· ,λn是n

个不全相等的正数. 于是A的特征多项式

又根据引理2.1 知, ΔA(λ)=λn −Q1λn−1+Q2λn−2−···+(−1)n−1Qn−1λ+(−1)nQn,比较系数可知, 对每个1 ≤i≤n,Qi=σi, 进而据引理2.2 得到

透过上面的推理, 定理2.1 完全依赖于Newton-Maclaurin 不等式这个深刻的工具,这样定理2.1 不是平凡的结果. 没有找到定理2.1 的脱离Newton-Maclaurin 不等式的证明, 这与Sz´asz 不等式具有本质的不同, Sz´asz 不等式是有非常初等的证明的, 见文献[5].

这里B跑遍行列式为1 的正定Hermite 矩阵.

从情理上说, 定理2.1 应该是已知的结果, 但没有在已有的出版物上见到. 本文作者曾求教于矩阵论专家, 他们声称也没有见到定理2.1 这样的结论.

3 Hadamard 不等式与AM-GM 不等式的等价性

AM-GM 不等式是不等式理论里最重要的柱石之一, 存在许多令人叹为观止的证明和推广. 在阐述Hadamard 不等式和Sz´asz 不等式时, 文献[1] 写道:“Hadamard′s inequality, like the inequality connecting the arithmetic mean and the geometric mean,caught the fancy of mathematicians, with the result that there are a wide range of different proofs and numerous extensions of this result.”

现在, 要证明Hadamard 不等式与AM-GM 不等式的等价性, 这个结论为文献[1]的这段文字提供了一个直接的, 有力的注解.

定理3.1Hadamard 不等式与AM-GM 不等式是等价的.

在给出定理3.1 的证明之前, 先证明下面的引理.

引理3.1若A=(aij)n×n为n阶Hermite 矩阵, 则存在n阶酉矩阵U使得

其中trA为矩阵A的迹.

引理得证.

显然B也是正定Hermite 矩阵, 设B的特征值为λ1,λ2,··· ,λn, 则λi>0 且

等号成立当且仅当B的特征值均为1, 当且仅当B=I, 当且仅当

反过来, 若A=diag(a11,a22,··· ,ann) 为n阶对角矩阵, 且aii>0, 则A是正定矩阵. 由引理3.1 可得, 存在n阶酉矩阵U使得

由Hadamard 不等式可得

另外, 从文献[1-2,4] 知, Hadamard 不等式和AM-GM 不等式都有相互独立的证明, 定理3.1 表明它们是等价的.

4 平均

已经存在许多关于Hadamard 不等式的证明, 上节从AM-GM 不等式出发的证明应该是早已经存在的, 在此写出来是为了文章的完整性, 更是为了突出“平均” 思想的威力, 这种简单朴实的思考方式常常被忽视了. 下面再举两例来阐释这种方法, 而结论也是早为人知的.

证明由于A,B是半正定矩阵, 则A+B半正定, 设r(A+B)=r, 则存在可逆矩阵Q, 使得

设

其中A11和B11是r阶矩阵. 显然A1和B1半正定, 从而对满足r+1 ≤i≤n的i,有aii=bii=0. 进一步, 由于A1是半正定Hermite 矩阵, 故可得

结论成立.

例4.2(Minkowski 不等式) 设A,B是两个n阶正定Hermite 矩阵, 则

且“=” 成立当且仅当存在k>0, 使得B=kA.

证明由于A,B是正定矩阵, 则A+B正定, 从而存在可逆阵P, 使得