一种高效的动态图最大加权独立集求解算法
2021-07-23祁才云周军锋
祁才云,周军锋,杜 明
(东华大学,上海 200000)
0 引言
图是用来描述个体之间相互联系的一种复杂的数据结构[1]。在现实世界中,可将网络[2-3]、计算机视觉[4-5]、社交网络[6-7]、无线传感网络[8]等数据抽象为图模型。在实际生活中,最大加权独立集问题[9-14]广泛应用于解决各项问题,例如分配分布式系统中的资源、避免无线网络中的多址信道干扰等。
动态图[15-17]是指会随时间发生变化的图数据。例如,在现实世界中,个体的数量或个体间的联系发生变化时,图也相应的发生着变化,可以把这种图的变化抽象为动态图。随着数据的快速变化,在动态图上获取有价值的信息也吸引了大量研究者的关注。在分布式系统中,当系统中计算机的数量、计算机间的干扰频繁发生变化时,可以不用考虑整个系统,只需单独观察发生变化的计算机或计算机间的干扰,快速搜索图的最大加权独立集,进而减少数据传输过程中数据丢失。在无线网络中,用户的数量以及信号传播中的干扰会随时发生变化,在这些变化发生后,需要快速获取该图的最大加权独立集,进而避免发生信号干扰。
综上所述,最大加权独立集问题在现实生活中应用广泛。当图的结构发生变化时,现有的算法只能重新搜索最大加权独立集,因此无法高效地获取结果。
针对上述问题,本文首次提出动态图上的最大加权独立集问题,并设计出支持高效更新的近似算法LSWTwo,当更新操作发生时,该算法考虑到受影响的点是距离为2范围内的点,因此,通过只处理该范围的点,避免对最大加权独立集的重新搜索,提升更新操作的效率。
1 相关工作
1.1 问题定义
给定顶点加权无向图G= (V,E,ω)以及该图的最大加权独立集,其中V表示G中顶点的集合,E表示G中边的集合,ω表示顶点权值的集合。对于图G中的顶点v,用N(v)表示该顶点的所有邻居顶点。
定义1 独立集给定无向图G= (V,E),图中互不相邻的顶点构成的集合称为独立集。
定义2 最大独立集(Maximum Independent Set,简称 MIS):给定无向图G= (V,E),称顶点个数最多的独立集为最大独立集。
定义3 最大加权独立集(Maximum Weight Independent Set,简称 MWIS):给定顶点加权无向图G= (V,E,ω),称权值总和最大的独立集为最大加权独立集。
问题定义给定T时刻的顶点加权无向图G= (V,E,ω)以及该图的最大加权独立集MWIS(T),T1时刻对图G进行一次更新操作得到G',求图G'的最大加权独立集MWIS(T1)。
1.2 相关算法
本节介绍静态图上搜索最大加权独立集的近似算法DtTwo[18]。DtTwo算法首先使用等价约简规则降低问题的规模,然后使用贪心算法得到最大加权独立集,接下来将详细介绍DtTwo。
1.2.1 等价约简规则
定理1:(单顶点约简)给定一个顶点v∈V,如果ω(v) >ω(N(v)),则v必定属于MWIS(G),因此N(v)中的顶点可以删除,得到MWIS(G)=MWIS(G') ∪ {v},其中G'=G(N(v) ∪v)。
证明:假设顶点v不属于MWIS(G),因此顶点v至少有一个邻居属于MWIS(G),可以用v替换MWIS(G)中v的邻居,然后得到一个新的独立集MWIS' (G),因为ω(MWIS′(G) ) >ω(MWIS(G)),所以ω(MWIS′(G) ) >ω(MWIS(G)),可得顶点v必属于MWIS(G)。
定理2:(双顶点约简)给定两个顶点v,u∈V和它们的邻居P,如果ω(v) +ω(u)>ω(P),则v和u必属于MWIS(G),因此P中的顶点可以删除,得到MWIS(G) =MWIS(G′ ) ∪ {v,u},其中G′=G(P∪v∪u)。
DtTwo算法首先使用上述两个等价约简规则对原始图进行等价约简,降低问题的规模。
1.2.2 贪心算法
当图无法使用等价约简规则时,选择权重最大的顶点为MWIS(G)中的顶点,同时删除该顶点的所有邻居,每次选择顶点后迭代使用等价约简规则,重复此过程,直至图为空,得到MWIS(G)。
2 LSWT wo算法
LSWTwo算法包含处理删点、增边和删边更新的方法。
2.1 删点更新
删点更新分为两种情况:(1)当删除的顶点v不属于MWIS(T)时,删除该顶点v并不影响MWIS(T1),所以MWIS(T1)和MWIS(T)相同;(2)当删除的顶点属于MWIS(T)时,顶点v的邻居u必定不属于MWIS(T),此时需要判断顶点u是否有邻居顶点属于MWIS(T1),若有,则顶点u必定不属于MWIS(T1),反之顶点u可能属于MWIS(T1),最后将所有可能属于MWIS(T1)的顶点合起来生成一个子图,对子图进行最大加权独立集的搜索,搜索的最大加权独立集与MWIS(T) v的并集为MWIS(T1)。删点更新的具体过程如算法1所示。
算法1 RV
输入:删除的顶点v、T时刻图G= (V,E,ω)和已知的最大加权独立集MWIS(T)
输出:T1时刻的最大加权独立集MWIS(T1)
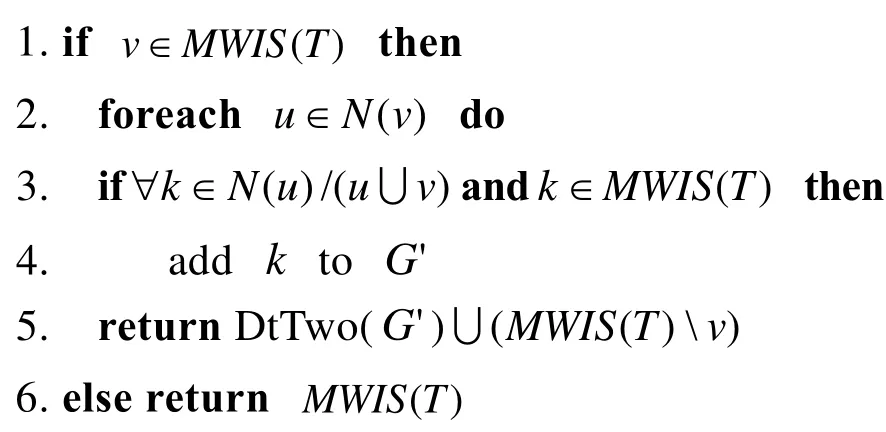
下面以图1为例介绍RV的算法过程。
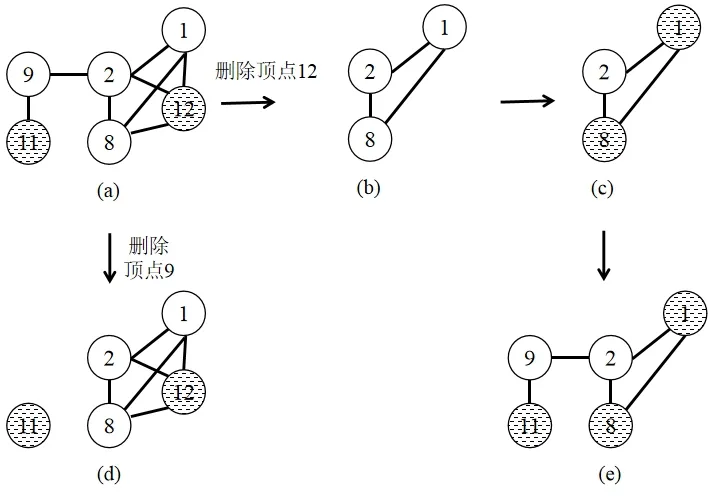
图1 删点更新示意图Fig.1 Schematic diagram of delete point
例如,针对图1的图a,图中带有阴影的顶点表示属于MWIS(T),图 a的最大加权独立集为{11,12}。删点更新分为两种情况:(1)假设删除的顶点属于MWIS(T),例如删除权值为 12的顶点,因为该顶点属于MWIS(T),所以删除顶点时需要判断该顶点的邻居是否可能属于MWIS(T1),权值为12的顶点的邻居有1、2、8三个顶点,通过遍历可以发现1、2、8顶点的所有邻居(除顶点12以外)都不属于MWIS(T),所以这三个顶点都可能属于MWIS(T1),于是生成由1、2、8三个顶点组成的子图,如图b所示,子图b的最大加权独立集为{1,8},如图c所示,最后将子图b的最大加权独立集与MWIS(T){12}合并,得到MWIS(T1)为{1,8,11}(如图 e所示)。(2)假设删除的顶点不属于MWIS(T),例如删除权值为 9的顶点,因为该顶点不属于MWIS(T),所以直接删除该顶点及其所有的边即可,如图 d所示,MWIS(T1)与MWIS(T)相同,都为{11,12}。
2.2 增边更新
增边更新分为两种情况:(1)当增加的边的两端顶点有一个顶点不属于MWIS(T)时,增边后并不影响MWIS(T1),所以MWIS(T1)和MWIS(T)相同;(2)当增加的边的两端顶点都属于MWIS(T)时,该操作会对MWIS(T1)造成影响,增加的边两端顶点必有一个属于MWIS(T1),另一个不属于MWIS(T1),本节方法将权值大的顶点添加到MWIS(T1),减少权值的损失,权值小的顶点v则必定不属于MWIS(T1),所以顶点v的邻居可能属于MWIS(T1),将所有可能属于MWIS(T1)的顶点集合起来生成一个子图,对子图进行最大加权独立集的搜索,搜索的最大加权独立集与MWIS(T) v的并集为MWIS(T1)。增边更新的具体过程如算法2所示。
算法2 AE
输入:增加的边的两端顶点v和u、T时刻图G= (V,E,ω)和已知的最大加权独立集MWIS(T)
输出:T1时刻的最大加权独立集MWIS(T1)

以图 2为例介绍 AE的算法过程。针对图 2的图a,图中带有阴影的顶点表示属于MWIS(T),图a的最大加权独立集为{8,11}。增边更新分为两种情况:(1)假设增加的边两端顶点时需要将权值小的顶点 8从MWIS(T)中剔除,当都属于MWIS(T),例如增加11和8之间的边,因为顶点11和顶点8都属于MWIS(T),所以在增边顶点8被剔除时,需要判断该顶点的邻居是否可能属于MWIS(T1),通过图a可以发现顶点8的邻居1、2、3的所有邻居(除顶点8以外)都不属于MWIS(T),所以这三个顶点都可能属于MWIS(T1),于是将1、2、3三个顶点添加到子图中,如图b所示,子图b的最大加权独立集为{2,3},如图c所示,最后将子图b的最大加权独立集与MWIS(T){8}合并,得到MWIS(T1)为{2,3,11},如图e所示。(2)假设增加边的两端顶点含有不属于MWIS(T)的顶点,例如增加顶点2和3之间的边,因为含有不属于MWIS(T)的顶点,所以直接增加顶点2和3之间的边即可,如图d所示,MWIS(T1)与MWIS(T)相同,都为{8,11}。
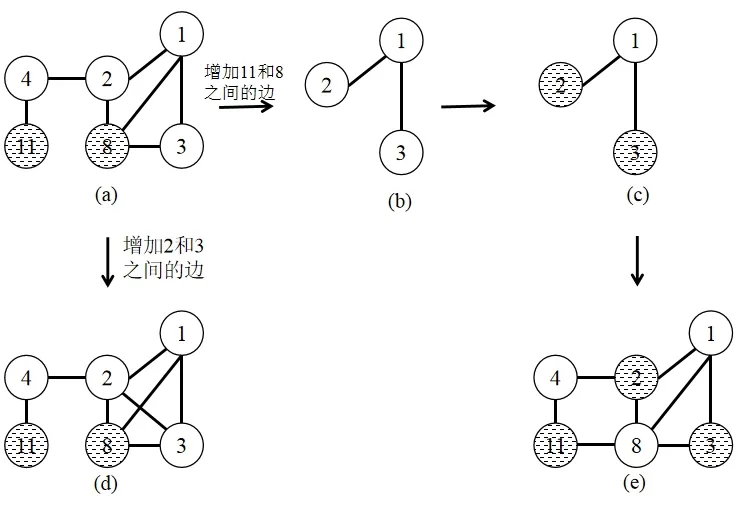
图2 增边更新示意图Fig.2 Schematic diagram of added edge
2.3 删边更新
删边更新分为两种情况:(1)当删除的边的两端顶点都不属于MWIS(T)时,删边后并不影响MWIS(T1),所以MWIS(T1)和MWIS(T)相同;(2)当删除的边的两端顶点中有一个顶点属于MWIS(T)时,该更新会对MWIS(T1)造成影响,判断两端顶点中不属于MWIS(T)的顶点是否属于MWIS(T1)即可。删边更新的具体过程如算法3所示。
算法3 RE
输入:删除边的两端顶点v和u、T时刻的图G= (V,E,ω)和已知的最大加权独立集MWIS(T)
输出:T1时刻的最大加权独立集MWIS(T1)

以图3为例介绍RE的算法过程。
例如,针对图3的图a,图中带有阴影的顶点表示属于MWIS(T),图 a的最大加权独立集为{8,11}。删边操作主要分为两种情况:(1)假设删除的边两端顶点含有属于MWIS(T)的顶点,例如删除顶点8和顶点3之间的边,因为顶点8属于MWIS(T),所以在删除边后需要判断顶点 3是否可能属于MWIS(T1),因为顶点 3没有属于MWIS(T)的邻居(除顶点8外),所以顶点3属于MWIS(T1),MWIS(T1)为{11,8,3},如图b所示。(2)假设删除的边两端顶点都不属于MWIS(T),例如删除顶点2和顶点1之间的边,因为两个顶点都不属于MWIS(T),所以直接删边即可,如图 c所示,MWIS(T1)与MWIS(T)相同,都为{8,11}。

图3 删边更新示意图Fig.3 Schematic diagram of edge deletion
2.4 算法分析
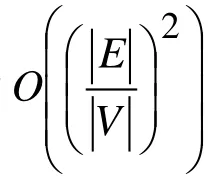
3 实验分析
3.1 实验环境
实验所使用的硬件配置是 Intel(R) Core(TM)i5-6600 CPU @3.30 GHz,8.00 GB RAM 以及Windows 7专业版;实验的运行环境为Microsoft Visual Studio 2015。实验用于比较的算法是DtTwo算法和处理单一更新的RV、AE和RE算法。以上算法均采用C++语言实现。
3.2 数据集
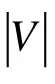
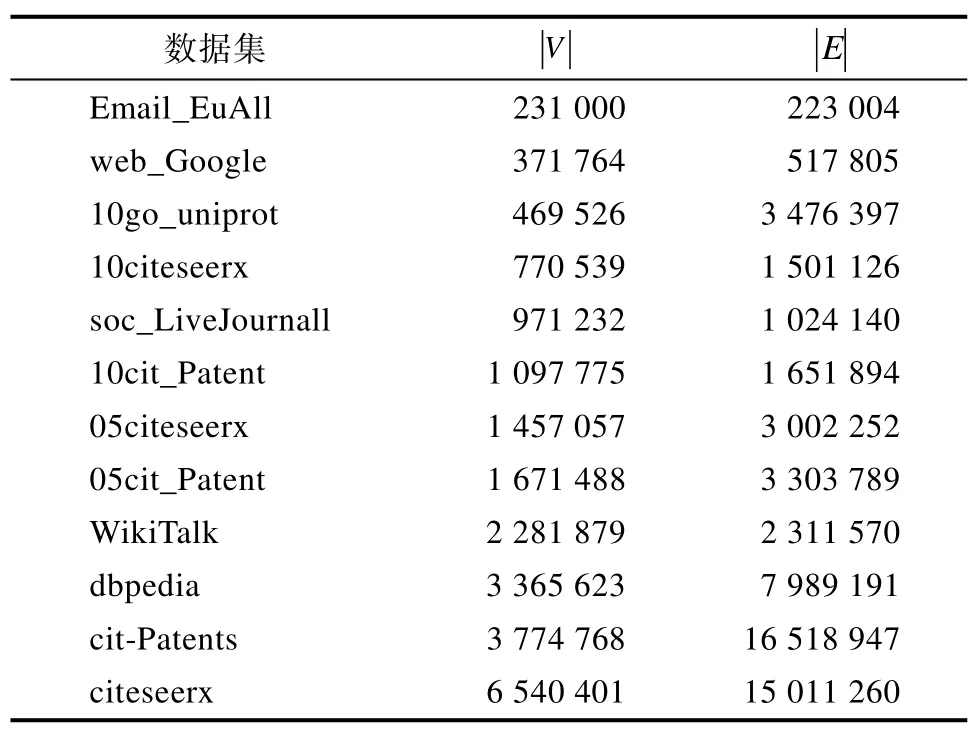
表1 数据集统计信息Tab.1 Data set statistics
3.3 性能比较分析
本文提出的RV、AE、RE方法的初始加权独立集均为已知质量最高的最大加权独立集。
表2、表 3和表4分别展示的是处理单一删点、增边、删边更新的最大加权独立集的权值总和比较。观察发现本文提出的RV、AE和RE方法搜索的最大加权独立集的权值总和均大于DtTwo方法搜索的最大加权独立集的权值总和。
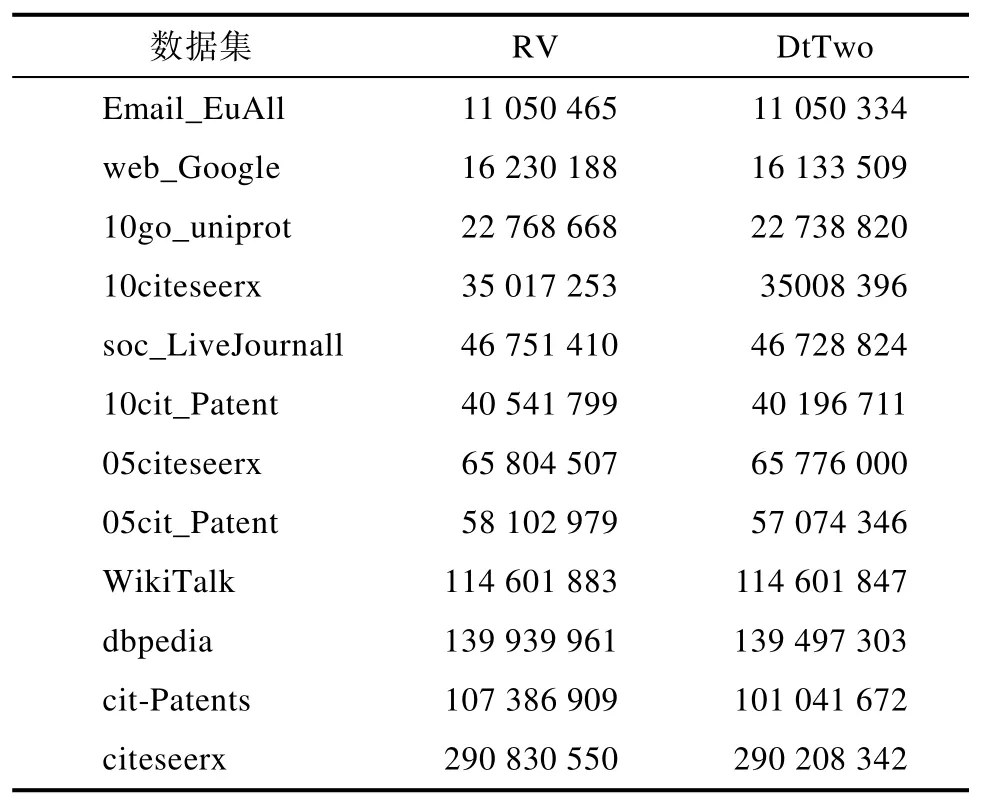
表2 删点更新的最大加权独立集的权值总和Tab.2 The sum of the weights of the largest weighted independent set updated by deleting points
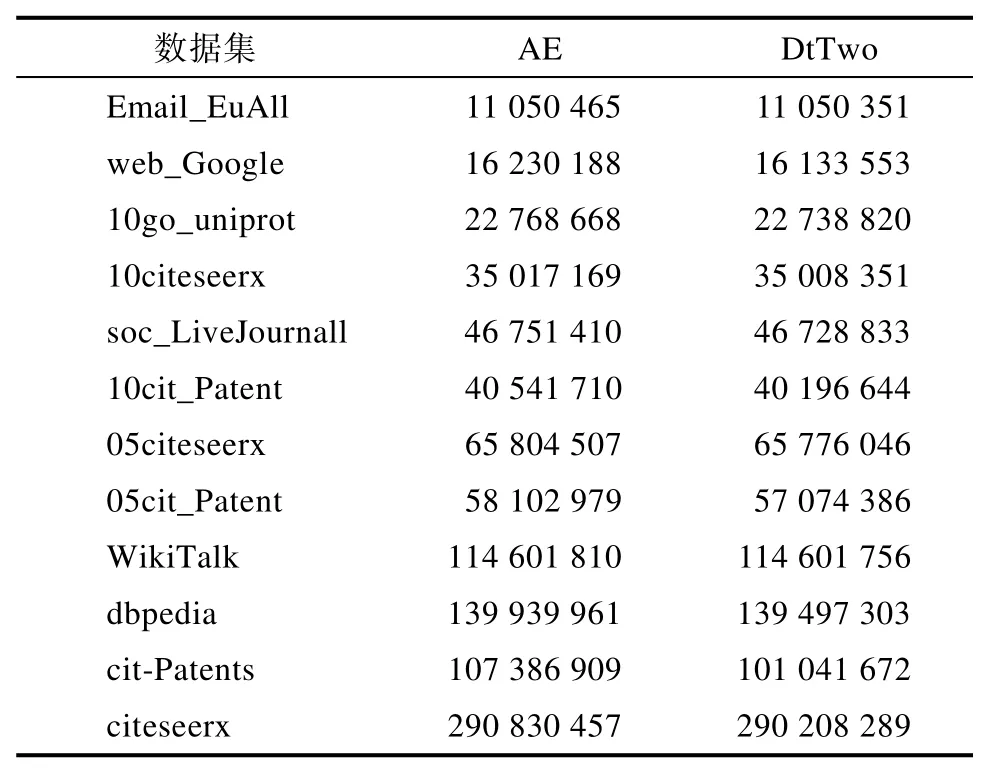
表3 增边更新的最大加权独立集的权值总和Tab.3 The sum of the weights of the largest weighted independent set updated by the incremental edge
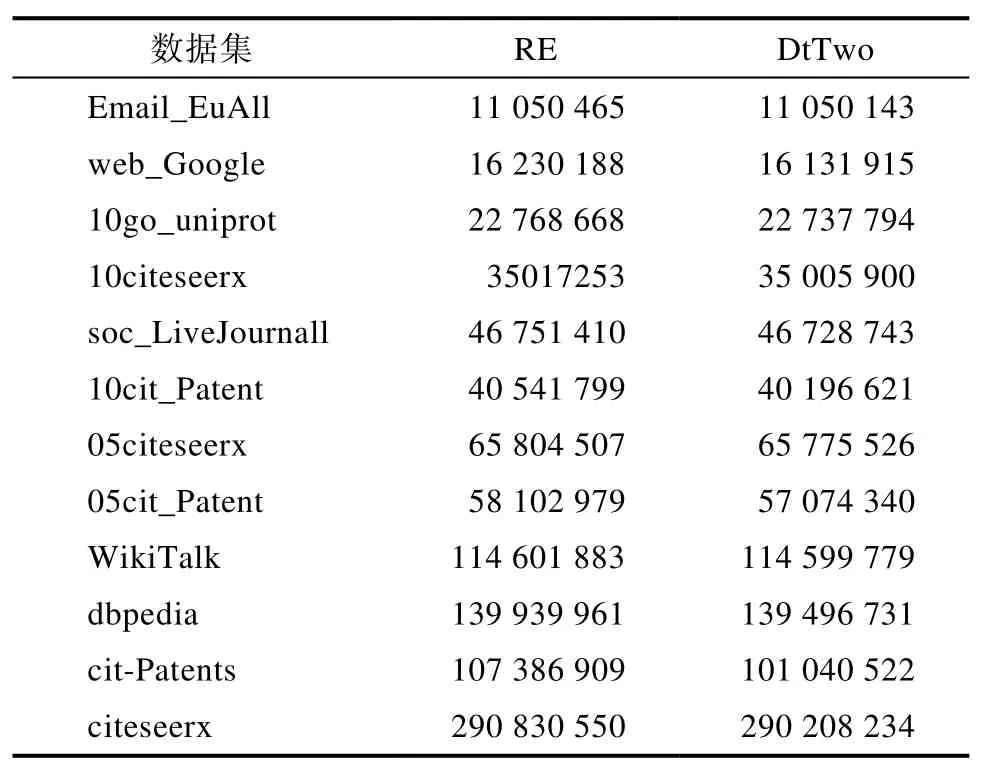
表4 删边更新的最大加权独立集的权值总和Tab.4 The sum of the weights of the largest weighted independent set updated by deleting edges
表 5展示的是删点更新的时间比较,观察可以发现RV方法中有多个值为0的数据集,原因是删除的顶点未影响到更新后的图的最大加权独立集;在其它数据集上,RV方法的时间至少比DtTwo快 70倍,时间差最大的数据集是 soc_LiveJournall,RV比DtTwo快2649倍。

表5 删点更新时间(ms)Tab.5 Delete point update time (ms)
表6展示的是增边更新的时间比较。观察可以发现AE方法中有多个值为0的数据集,原因是增加的边未影响更新后的图的最大加权独立集;在其它数据集上,AE方法至少比DtTwo快70倍,时间差最大的数据集是 WikiTalk,RV比DtTwo快45815倍。
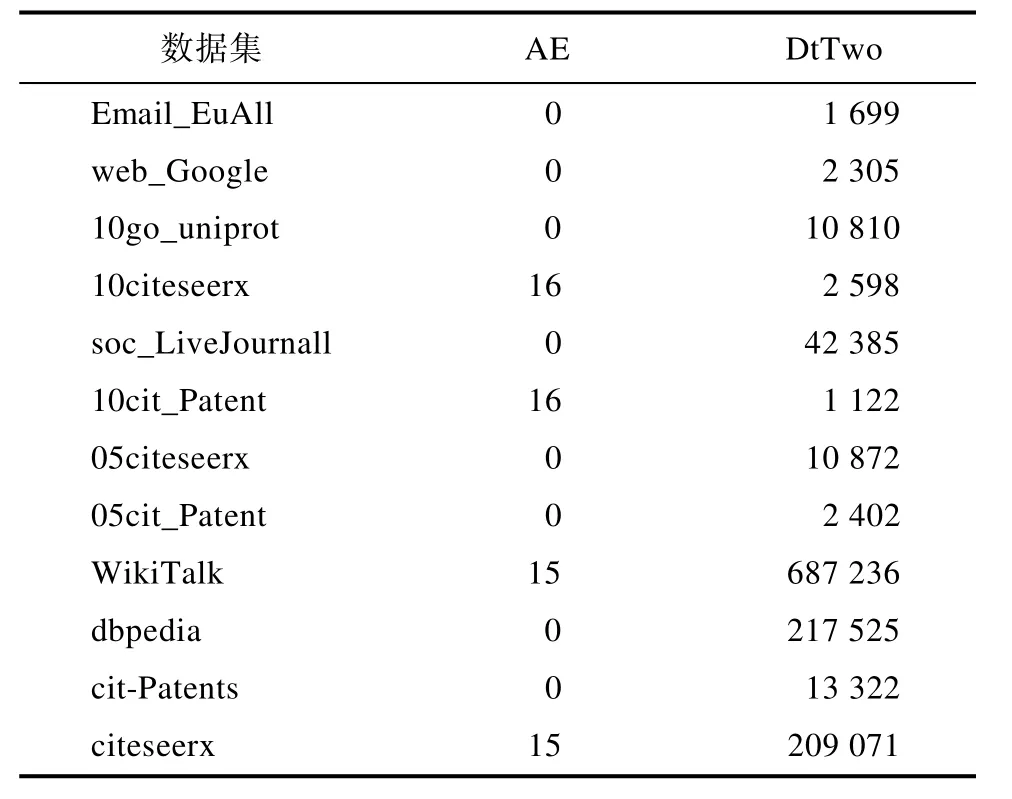
表6 增边更新时间(ms)Tab.6 Increased update time (ms)
表7展示的是处理删边更新的时间比较。观察可以发现RE方法中有多个值为0的数据集,原因是删边未影响更新后的图的最大加权独立集;在其它数据集上,RE方法的时间至少比DtTwo快70倍,时间差最大的数据集是WikiTalk,RE比DtTwo快2649倍。
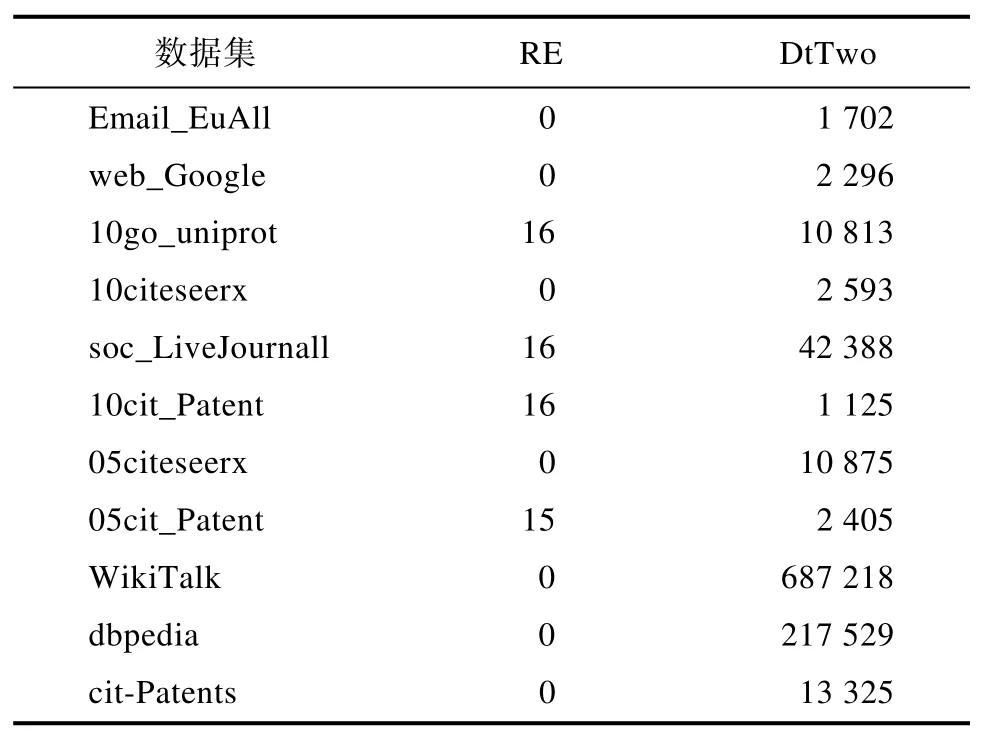
表7 删边更新时间(ms)Tab.7 Delete edge update time
4 结论
针对动态图上的最大加权独立集问题,现有的解决方案是重新计算整个图的最大加权独立集。为了加快求解的效率,本文提出了一种只考虑被操作顶点距离为 2范围内顶点的近似算法LSWTwo。实验结果表明,LSWTwo算法在不降低结果质量的前提下,将搜索的时间降低了80%~98%。
