一种无容量设施选址问题的新颖离散差分演化算法
2021-07-23张发展
张发展,张 潼
(河北地质大学 信息工程学院,河北 石家庄 050031)
0 引言
无容量设施选址问题(UFLP)[1]是由Kuehn和Hamburger于1963年首次提出的一个重要的组合优化问题。UFLP不仅对于学校、工厂、仓库、消防站、医院等基础设施的选址具有重要的应用价值[2-3],而且在资源配置、资金预算、物流运输、计算机网络和计算机视觉等领域具有重要的理论意义[4-7]。
近年来,国内外学者对 UFLP的求解算法进行了广泛的研究。Galvão和Raggi[8]提出了一种求解UFLP一般0-1公式的三阶段精确方法。Conn和 CornuéJols[9]提出了一种基于凝聚对偶的正交精确解求解超线性规划的新方法投影,并用于求解UFLP问题。Charikar和Guha[10]提出了一种简单的贪婪局部搜索算法,在 (2/ )O n∊时间内达到了2.414+∊的近似比。Takaya等人[11]和Atta[12]等人先后提出了利用萤火虫算法(FA)和猴群算法(MA)求解UFLP的方法,但是他们都没有给出大规模UFLP实例的计算结果。通过上述文献可以看出,精确算法在求解大规模UFLP实例时是非常耗费时间的,而非精确算法尤其是演化算法的求解速度远远快于精确算法。目前,如何利用演化算法快速高效地求解UFLP已经成为一个热点问题。因此,本文研究如何利用DE求解UFLP问题,本文首先提出了一个新型传递函数Ntf,将DE中的个体的实向量转换为二进制向量,以适用于直接求解二元优化问题。然后基于 Ntf给出了一种新的离散差分演化算法(N-DisDE),并利用N-DisDE提出了求解UFLP的一个新的高效方法。
1 UFLP 问题的定义和数学模型
UFLP的定义一般描述为:给定客户的集合K= {k1,k2,… ,kn},其中m为客户的数量,ki表示第i个客户。给定可以开放的设施集合S={s1,s2,… ,sn},其中n为设施数量,sj表示第j个设施。给定一个m×n的服务矩阵D= [dij]m×n,其中dij表示当第i个客户从第j个设施获得服务时的服务成本。G= {g1,g2,… ,gn}是设施固定开放成本的集合,其中gj表示第j设施开放所需要的开放成本。
首先定义了两个二进制变量yij和xj如下:


根据上述定义,UFLP的数学模型描述如下:
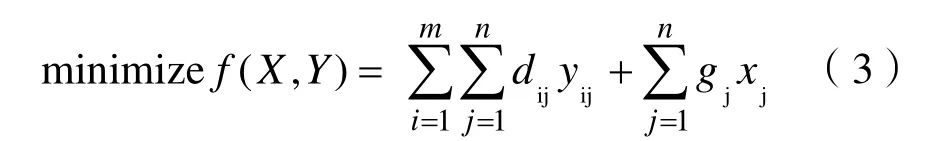
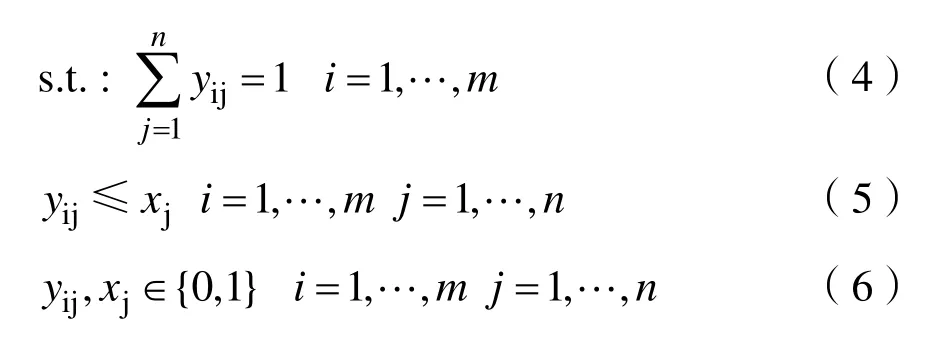
2 新型传递函数
近年来,传递函数已经成为将连续型演化算法转换为离散演化算法的重要方法之一。目前,已有的转换函数可以分为两类:S型传递函数和V型传递函数[13-14]。在表1中给出了8个已有的S型和V型转换函数的函数公式,其中S型转换函数分别命名为S1 ~S4,V型转换函数分别命名为V1 ~V4。

表1 S型转换函数和V型转换函数Tab.1 S-shaped conversion function and V-shaped conversion function
book=28,ebook=32本文受S型和V型传递函数的启发,提出了一个新型转换函数,命名为Ntf。转换函数Ntf的计算公式为:

3 利用N-DisDE求解UFLP
3.1 N-DisDE
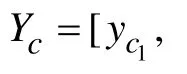
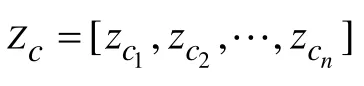
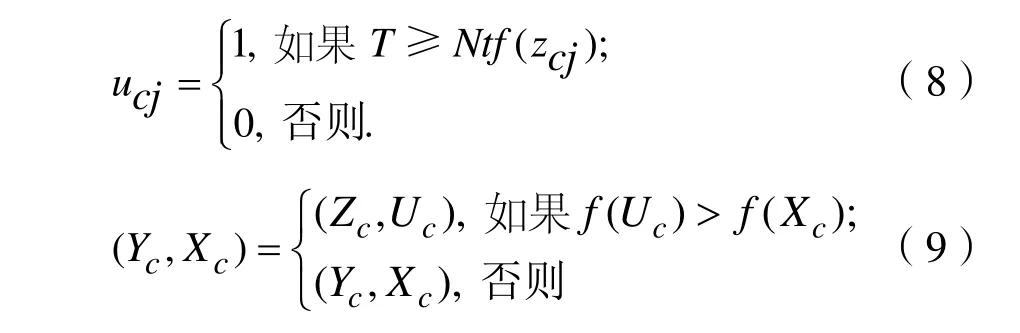
其中, T∈(0,1) 是一个预先设定的阈值,本文设为0.5。
3.2 利用N-DisDE求解UFLP
输入:一个UFLP实例,参数A,N,CR,T,FS和MI;
输出:最好解B和最好值f( B, Q).


在算法 1中,step(1)的时间复杂度为O(N×n);step(2)~step(7)的时间复杂度为O(N×m×n2);step(8)的时间复杂度为O(N);step(9)~step(18)的时间复杂度为O(MI×N×m×n2);因此,算法 1的时间复杂度为O(N×n) +O(N×m×n2)+O(N)+O(MI×N×m×n2)。当m(客户个数),N,MI是关于n的多项式时,算法1为具有多项式时间复杂度的演化算法。
4 计算结果与分析
本文所有计算在配置为(英特尔)Intel(R)Core(TM)i5-7500 CPU@3.40GHz(3401 MHz)和4GB的RAM 2.90ghz的微型计算机上进行,编程语言为C,编译环境为Code:Blocks。
4.1 UFLP 实例
我们利用 15个来自 OR-library[15]的 UFLP benchmark实例对EGTOA与上述算法进行比较,这15个benchmark实例根据它的规模大小分为4类:第一类是16×50(即16个设施和50个客户)的小规模实例,编号分别为cap71~cap74;第二类是25×50(即25个设施和50个客户)的中等规模实例,编号分别为 cap101~cap104;第三类是50×50(即50个设施和 50个客户)的中等规模实例,编号分别为 cap131~cap134;第四类是100×1000(即100个设施和1000个客户)的大规模实例,编号分别为 capA~capC。四类 UFLP实例的规模大小与最优值见表2所示。
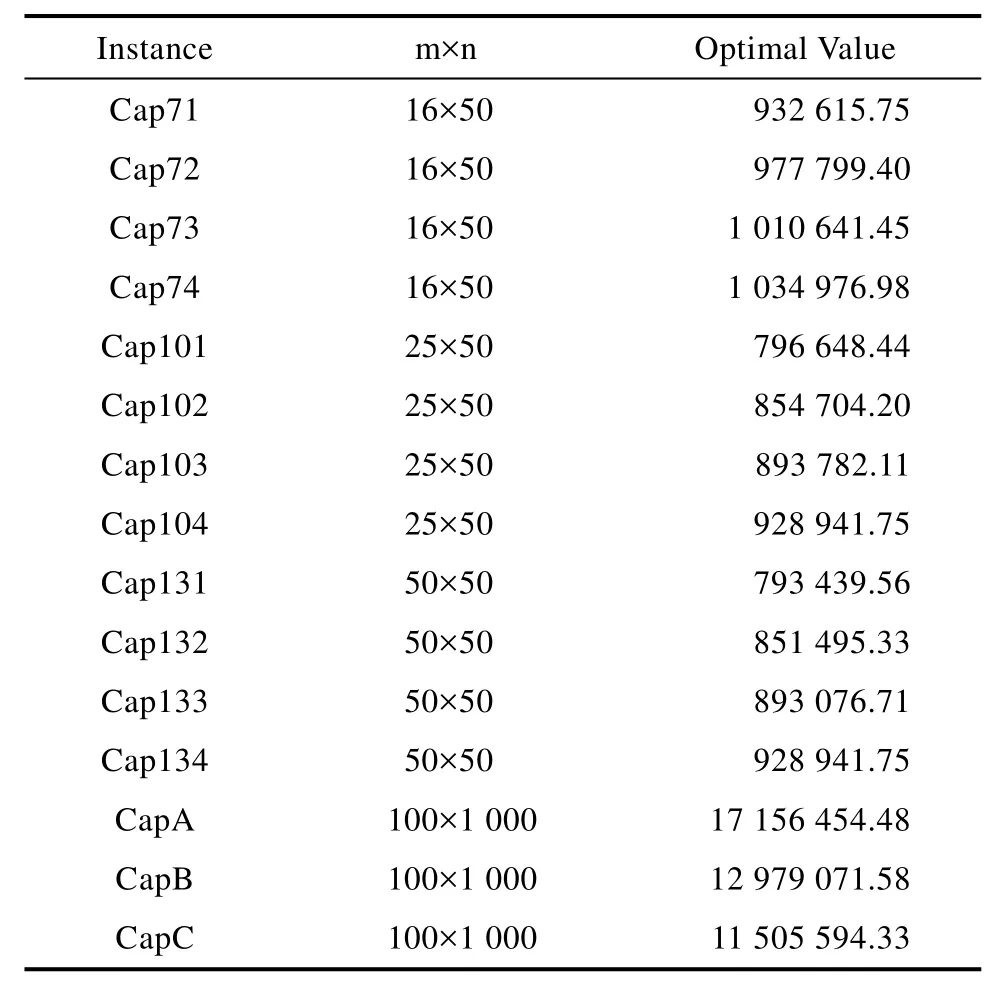
表2 UFLP 实例Tab.2 Th e UFLP instances
4.2 计算结果比较与分析
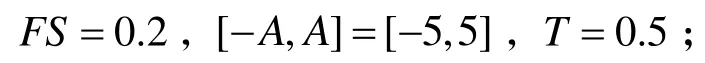
从表3可以看出,N-DisDE,HBDE 和BPSO对于第一类UFLP实例均能100%求得最优值。从表4可以看出,对于第二类UFLP实例,N-DisDE和HBDE均能100%求得最优值,而BPSO对于实例Cap101和Cap103的求解结果较差,对于实例Cap102和Cap104的求解结果较好。从表5可以看出,对于第三类UFLP实例,HBDE的求解效果最好;N-DisDE对于实例Cap131的计算结果较差,30次独立运行中有29次可以求得最优值;BPSO的计算结果最差,仅对于实例Cap134的计算结果较好。从表5中可以看出,对于第四类大规模UFLP实例,N-DisDE的计算结果明显优于其他算法,不仅求解质量最好,且鲁棒性更佳;其次是BPSO,而HBDE的计算结果最差。
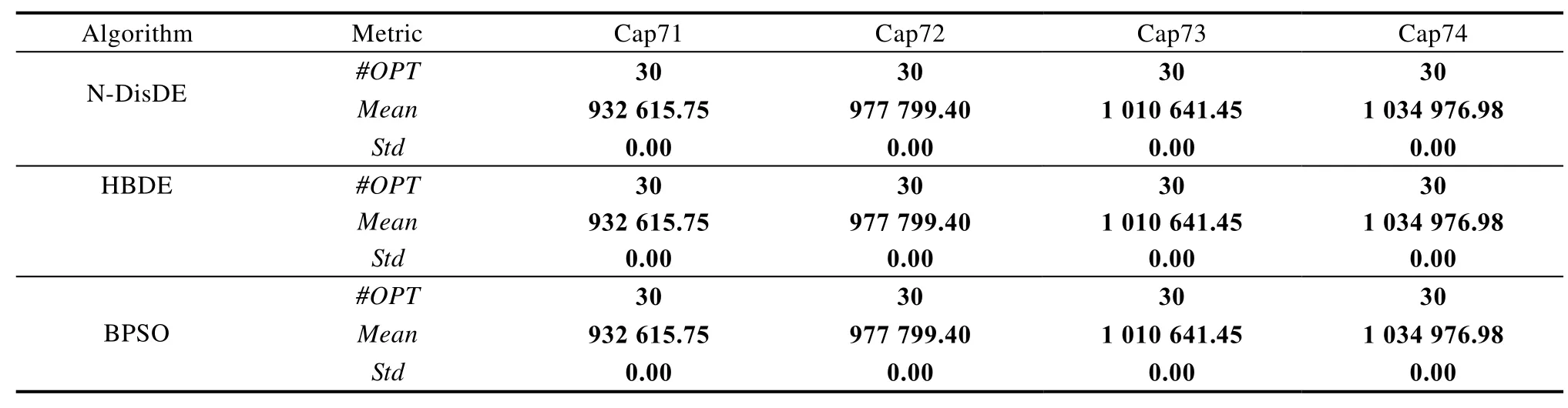
表3 N-DisDE ,HBDE和BPSO求解UFLP实例(16×50)的结果Tab.3 Calculation results of N-DisDE, HBDE and BPSO for solving UFLP instances (16×50)
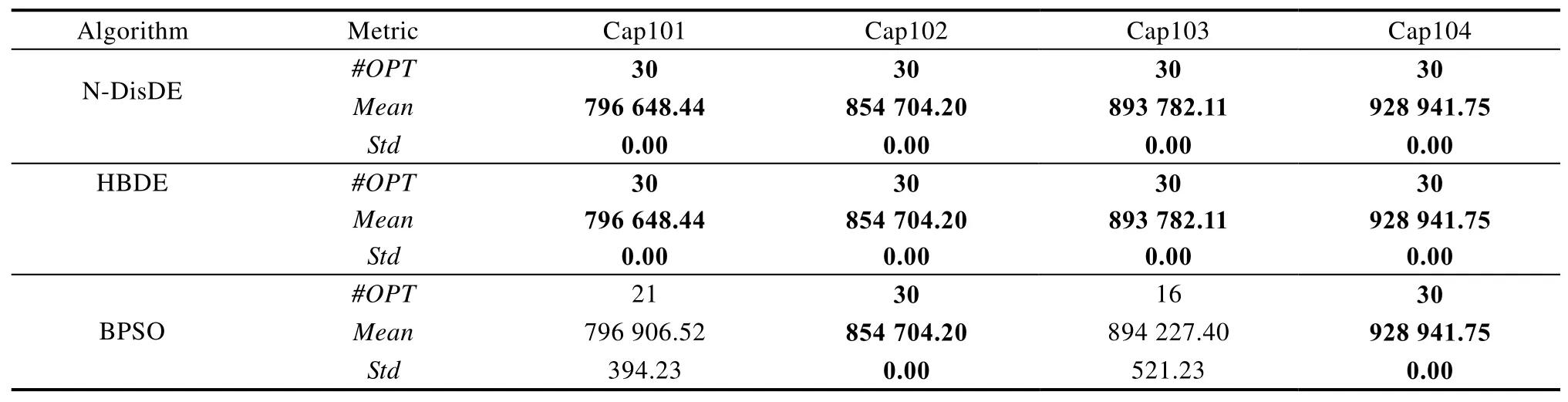
表4 N-DisDE ,HBDE和BPSO求解UFLP实例(25×50)的结果Tab.4 Calculation results of N-DisDE, HBDE and BPSO for solving UFLP instances (25×50)
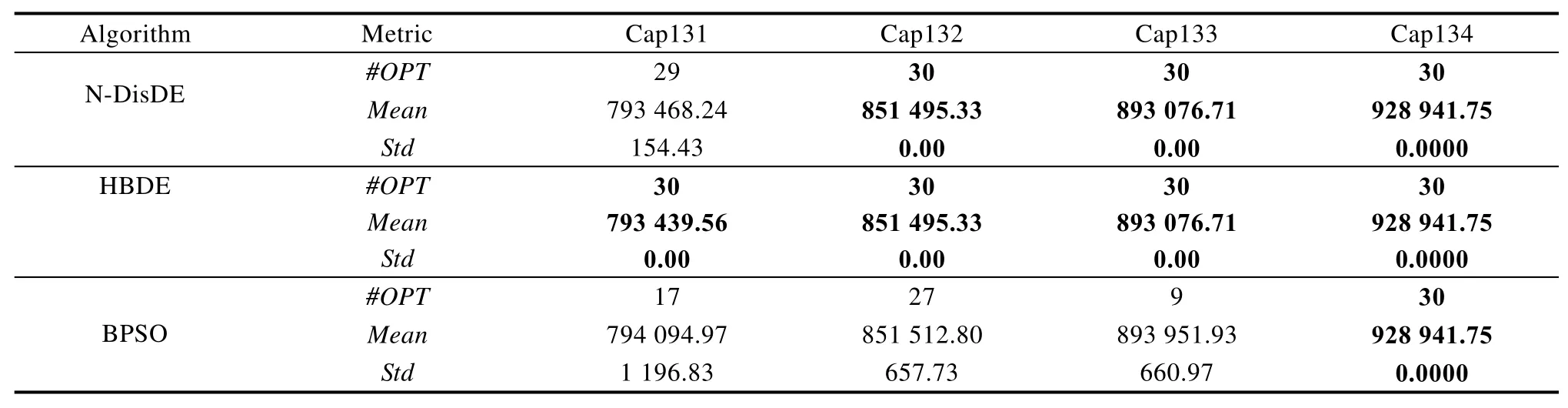
表5 N-DisDE ,HBDE和BPSO求解UFLP实例(50×50)的结果Tab.5 Calculation results of N-DisDE, HBDE and BPSO for solving UFLP instances (50×50)
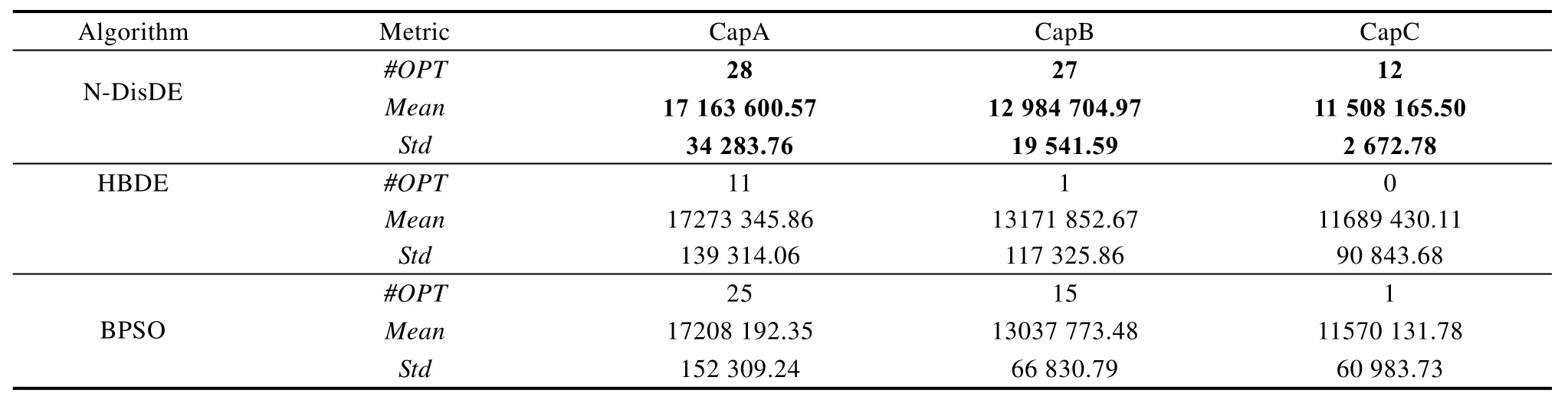
表6 N-DisDE ,HBDE和BPSO求解UFLP实例(100×1 000)的结果Tab.6 Calculation results of N-DisDE, HBDE and BPSO for solving UFLP instances (100×1 000)
5 结论与展望
本文受已有的S型和V型转换函数的启发,提出了一种新型转换函数Ntf,并在此基础上,给出了一种基于新型转换函数的离散差分演化算(N-DisDE)。为了验证N-DisDE的求解性能,本文通过求解4类不同规模UFLP实例,验证了算法的高效性和有效性,并通过与已有算法的计算结果比较表明:NDDE 比HBDE和BPSO的求解结果更优,算法的鲁棒性更佳,非常适用于求解大规模UFLP实例。
通过实验证明,本文提出的基于新型转换函数是非常成功的,这为连续演化算法离散化提供了一种新型函数。在未来研究中,我们将探索新型转换函数对其他算法的影响,如烟花算法(fireworks algorithm, FA)[18]和鸽群优化算法(pigeon-inspired optimization algorithm, PIO)[19]等。此外,我们将继续尝试利用 N-DisDE求解其他二元优化问题,例如各种背包问题[20-21],集合覆盖问题[22]等。
