一种TSMC共模电压频谱的三重傅立叶变换分析方法
2021-07-23苏建,耿强
苏 建,耿 强
(天津工业大学电气与电子工程学院,天津 300387)
0 引言
作为一种新型的“绿色”变频器,双级矩阵变换器(Two-Stage Matrix Converter,TSMC)不仅继承了矩阵变换器能量循环流动等优良的特性[1-3],而且拥有更为简单的换流和调制策略,因此在电动汽车、工业机器人等领域应用广泛[4-8]。当双级矩阵变换器正常工作时,会在电机负载的中性点处产生高频的共模电压[9-10],进而导致轴承损坏,同时在电磁耦合的作用下会产生电磁干扰,对整个系统的运行产生影响,因此充分了解共模电压的谐波分布规律对滤波器的设计具有现实意义。
目前针对TSMC输出谐波分析的主流方法为快速傅立叶变换(FFT),该方法的优点是方便快捷,实时性较强;但是当所截取的最终波形与三种频率不具备固定对应关系时,最终分析的谐波频谱存在不完整和相互重合的问题[11-13]。
为了解决这一问题,1975年Bird M等学者将原本用于通信系统的二重傅立叶解析方法用于PWM调制变换器的谐波分析中,得到了较为精准的各次谐波解析式[14]。文献[15]将二重傅立叶积分变换应用到超稀疏矩阵变换器低频谐波分析中,定量计算了线性区和过调制区输出电压和输入电流的低频谐波。文献[16]提出使用二重傅立叶变换计算脉宽调制信号频谱,并指出了其他类型调制的信号无法应用二重傅里叶变换的原因。
因此,三重傅立叶变换算法在二重傅立叶的基础上快速发展,学者Bingsen Wang将三重傅立叶积分变换和矩阵变换器的“直接传递函数法”相结合,从而得到了开关函数各频次谐波的频率和幅值[17]。文献[18]尝试将三重傅立叶级数和卷积定理相结合,然后对矩阵变换器的输出电压频谱进行定量分析,但是该方法的计算结果过于复杂,因此没有得到最简表达式。文献[19]基于载波调制方法,提出用三重傅立叶变换来获得矩阵变换器开关函数和合成终端量的精确光谱。
综上,本文在分析传统双空间矢量调制的基础上,提出利用三重傅立叶变换计算负载侧共模电压中各次谐波分量的分布规律和准确的谐波幅值解析解,并与FFT进行比较来证明其优越性,有助于完善双级矩阵变换器的谐波分析理论。
1 双级矩阵变换器传统双空间矢量调制
1.1 系统拓扑结构
双级矩阵变换器单输出阻感负载拓扑结构如图1所示,包括输入三相电源、LC输入滤波器、整流级、钳位电路、逆变级以及阻感负载。其中LC输入滤波器用来降低 TSMC的高频开关动作而产生的高频电流谐波;整流级由双向开关管组成,每个双向开关都带有两个反并联的快恢复二极管,两个 IGBT是共发射级结构,集电极和输入输出侧相连接,由此实现对电流方向的独立控制,达到能量双向流动的效果;钳位电路由一个单向二极管和电容组成,用来吸收由于高频开关动作而产生的尖峰电压,起到保护IGBT的作用;逆变级则是普通的两电平逆变器结构,阻感负载则采用星型连接方式。
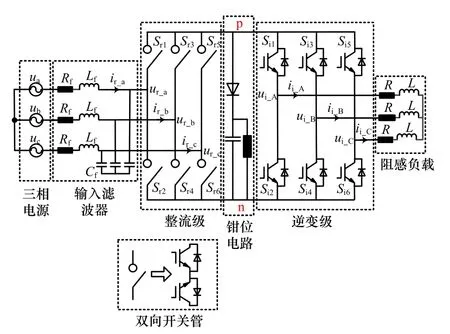
图1 TSMC-阻感负载系统拓扑结构图Fig.1 Topological structure diagram of TSMC-Resistance load system
首先为了保护整体结构,整流级在正常工作时需要避免过电流的现象,因此每一组上下的双向开关在一个控制周期内只能导通一个。根据图1所示,当上桥臂中的开关Sr1,3,5导通的时候,下桥臂的开关Sr2,4,6不可以导通,否则电流将不会经过逆变级的单向开关管而直接从直流母线电压的正负极流向负载,这样会短路网侧而发生过电流的现象,从而导致开关管损坏。根据上述约束条件,整流级开关需要满足的原则为:

式(1)中,ir_a代表整流级a相输入电流、ir_b代表整流级b相输入电流、ir_c代表整流级c相输入电流。
为了充分了解双级矩阵变换器的整个调制过程,需要对两级开关的模型进行介绍。将 TSMC整流级与逆变级的开关状态定义为:

式(2)中,x=i为逆变级开关状态,x=r为代表整流级开关状态,y=1,2,…,6为两种开关状态的开关序号。
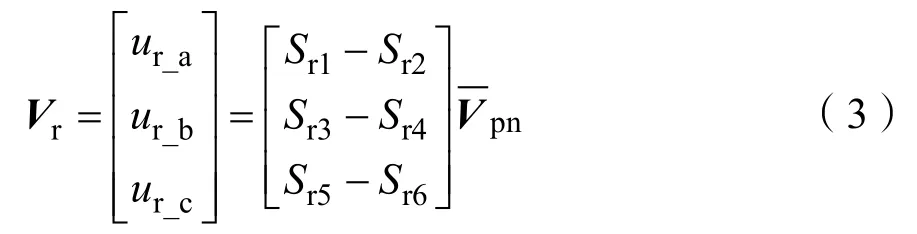
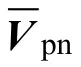
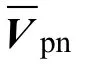
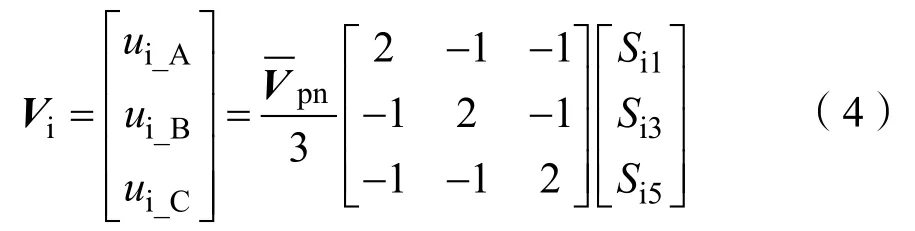
式(4)中,ui_A代表逆变级 A相输出电压、ui_B代表逆变级B相输出电压、ui_C代表逆变级C相输出电压、si1,3,5为逆变级3个单向开关的开关序号。
整流级三相输入电流 Ir与直流母线电流 Ipn的关系为:
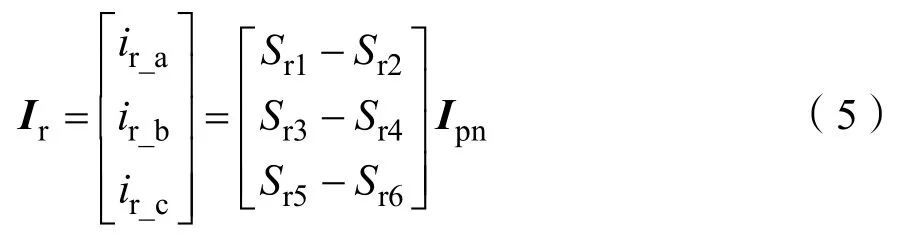
式(5)中,ir_a代表整流级a相输入电流、ir_b代表整流级b相输入电流、ir_c代表整流级c相输入电流、Ipn代表整流级输出的直流母线电流。
逆变级三相输出电流 Ii与直流母线电流 Ipn的关系为:
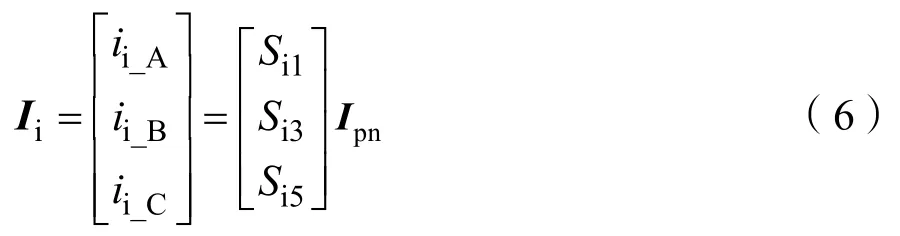
式(6)中,ii_A代表逆变级 A相输出电流、ii_B代表逆变级B相输出电流、ii_C代表逆变级C相输出电流。
设TSMC的输入相电压为:
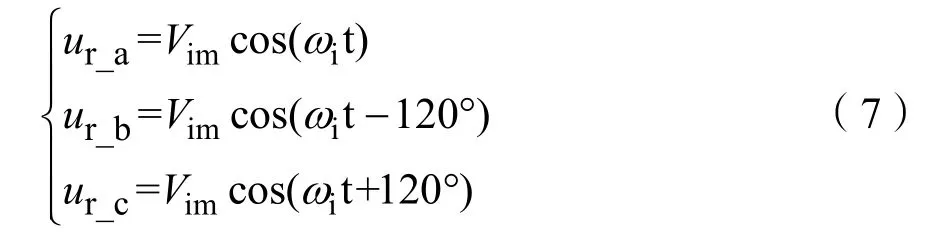
式(7)中,Vim和iω分别表示输入相电压的幅值与输入角频率。
1.2 传统双空间矢量调制
1.2.1 整流级调制
双级矩阵变换器的整流级为共集电极结构的双向开关,使得3个共发射极的IGBT由一个隔离电源供电,降低了整体驱动隔离电源的数量,同时兼具 IGBT共发射极结构的优势。由于双向开关的导通特性,因此整流级存在9种开关组合来对应 9个空间电流矢量,包括有效矢量 Ir1~Ir6和3个电流零矢量Ir0,当整流级一相桥臂上下开关导通,另两相桥臂开关全关断时,输入电流矢量为零矢量,故划分扇区后的输入电流空间矢量图如图2所示。
图2中,θin=z+π/6−(Lin–1)π/3,θin∈[0,π/3]],Lin代表整流级扇区序号,为了分析方便,令输入功率因数角为0,则z=2πfint,代表输入电流参考矢量与水平方向的夹角。设Ii_ref为参考电流矢量,可由其相邻有效空间矢量 Irm、Irn和零矢量 Ir0合成,表达式为:
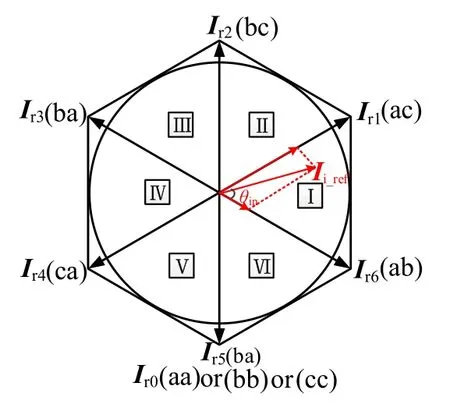
图2 整流级输入电流空间矢量图Fig.2 Space vector diagram of input current of rectifier stage
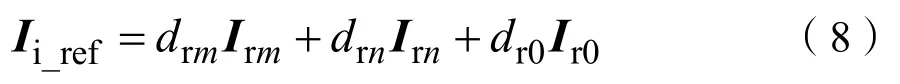
各矢量对应的占空比依次为 drm、drn和 dr0,计算公式为:
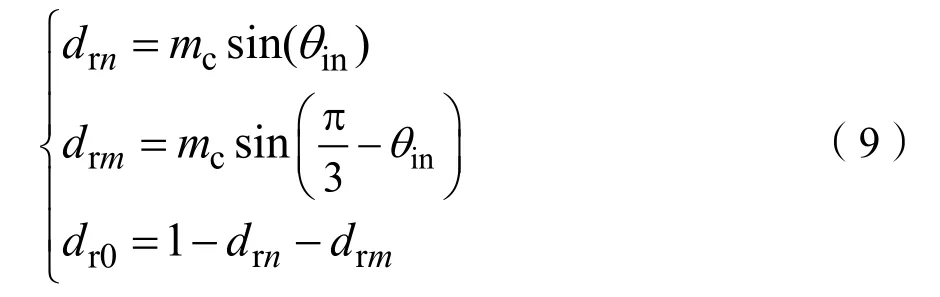
式(9)中mc为整流级的调制系数,取值范围为0≤mc≤ 1 。
1.2.2 逆变级调制
由于TSMC逆变级的拓扑结构与传统的两电平逆变器相同,而区别于传统的两电平结构,其在进行空间矢量调制时,两电平逆变器被供给的是恒定的直流母线电压;而TSMC逆变级得到的虚拟直流母线电压则由整流级经过 PWM调制斩波后的高频电压。但是TSMC逆变级的调制过程与两电平调制方式基本相同,即主要的思想就是利用逆变器空间电压矢量的切换来获得接近纯圆形的旋转磁场,当开关频率不是特别高时使得逆变级拥有更好的控制性能。
同理,为了保护逆变级的开关管,并且避免TSMC所连接的阻感负载发生开路而产生输出电压过大的现象,根据图1所示,当逆变级上桥臂中的开关 Si1,3,5导通的时候,下桥臂的开关 Si2,4,6不可以导通。因此逆变级开关状态的约束条件为:

式(10)中,Sij,Sij分别为逆变级A、B、C相上下桥臂的开关函数,其值为1代表导通,反之代表关断。化简得到输出电压的矢量表达式为:
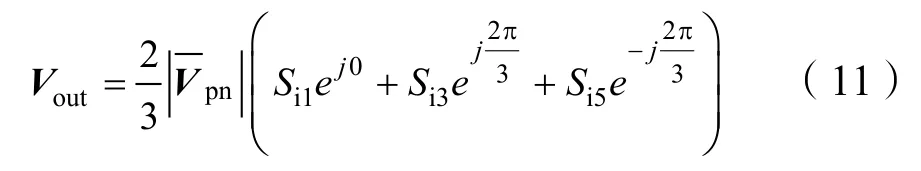
因此逆变级输出电压空间矢量图由 6个电压有效矢量Vi1~Vi6和2个电压零矢量Vi0组成,对应的电压空间矢量图如图3所示。
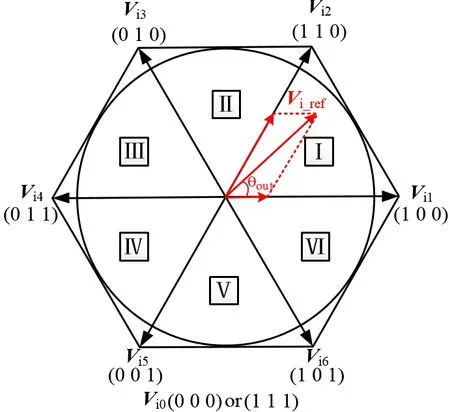
图3 逆变级输出电压空间矢量图Fig.3 Space vector diagram of output voltage of inverter stage
图3中,θout=y+π/6−(Lout–1)π/3,θout∈[0,π/3)],Lout代表逆变级扇区序号;y=2πfoutt,代表输出电压参考矢量与水平方向的夹角。以Vi1(1,0,0)为例,“1”代表A相上桥臂开关中仅有Si1为导通状态,第2位和第3位“0”分别代表B相和C相下桥臂开关中Si3和Si5为导通状态,A,B,C三相下桥臂开关与同相上桥臂开关呈互补关系。故设Vi_ref为参考电压矢量,可由其相邻有效空间矢量Viα、Viβ和零矢量Vi0合成,表达式为:
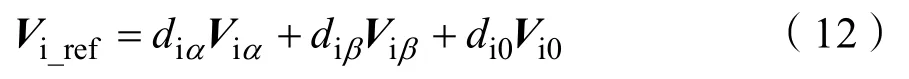
则各矢量对应的占空比依次为diα、diβ和di0,计算公式为:

式(13)中mv为逆变级的调制系数,取值范围为0≤mv≤ 1 。
1.2.3 整流级和逆变级协调控制
由于在双级矩阵变换器的整流级与逆变级之间不存在体积较大的电容储能硬件电路,并且整流级 PWM调制输出波动的直流母线电压,同时两级存在耦合现象,故为了得到理想的输入输出波形,我们需要对两级进行协调控制,并且安排合适的开关序列,同时保证整流级实现零电流换流。
由于整流级脉冲模式可以调整,故可以根据其分布状态是否对称将其分为:对称脉冲模式和非对称脉冲模式。对称脉冲模式,顾名思义就是整流级脉冲以控制周期的一半时间为分界线对称,虽然拥有良好的网侧输入波形和更低的谐波含量,但由于脉冲分布过多会导致开关切换次数过多而损耗过大,因此缺陷性较大。
因此本节的整流级选择不对称脉冲模式,将逆变级的零电压矢量分布于一个控制周期的两端和整流级矢量切换的时刻,从而保证整流级零电流换流。图4为TSMC非对称调制模式下整流级和逆变级的协调控制的安排图,根据调制的原理,整流级的载波可以等效为锯齿载波,而逆变级可以等效为不对称的三角载波。
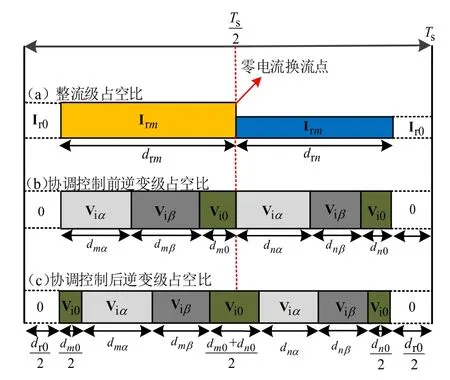
图4 两级协调控制的开关序列Fig.4 Switch sequence of two-stage coordinated control
故通过上述方式,可以合理的安排两级的占空比,最终得到理想的输入输出波形。
2 共模电压产生机理及危害
双级矩阵变换器的输出分量包括正序分量、负序分量和零序分量,其中差序分量即为期望得到的输出电压和电流。共模电压的准确定义即为负载中性点相对于参考电位点的电压值,它由一系列高频谐波组成,本质上是由零序分量所对应的开关动作合成的,则共模电压的表达式为:
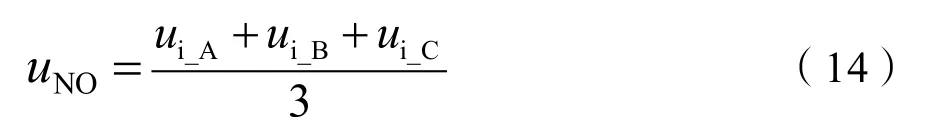
式(14)中,ui_A、ui_B、ui_C为输出相电压,因此输出电压的大小决定了共模电压的状态,再结合双级矩阵变换器的开关模型,得到共模电压由开关决定的定义式为:
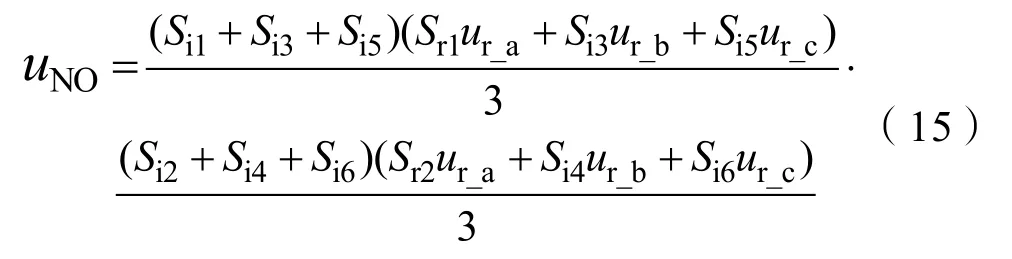
由式(15)可知,在输入电压保持不变的情况下,共模电压本质上由两级开关状态的组合决定。因此在传统双空间矢量调制策略下,共模电压的最终解析式与输入、输出和载波频率均相关。
当开关频率足够大或电压上升过快的时候,足够大的共模电压将会产生共模轴电流,从而引起电机轴承的损坏。此外,共模电压通过电磁耦合将在电机和大地之间产生高频的漏电流,当过大的漏电流流过地线的时候,将会引起电机接地保护的误动作。同时高共模电压变化率会产生很强的电磁干扰,对电机传动系统周围的装置产生不利影响。因此准确的共模电压分布规律可以为输出滤波器的设计提供参考,并且为共模电压的抑制方法提供新的思路。
3 共模电压谐波频谱分析
3.1 三重傅立叶级数
双级矩阵变换器作为一种全新的拓扑结构,通过控制两级开关的快速导通和关断得到期望的PWM电压电流波形,而傅立叶级数作为计算谐波含量的一种重要的数学计算方法,可以将周期信号展开成基波和各种非周期谐波分量之和。相比于传统的FFT分析方法,优点是得到各种谐波幅值的具体表达式,同时在被分析的波形无法与频率达成最佳的对应关系时,仍然可以得到较为准确的最终结果。
根据变量函数的数目不同,可以将基本的傅立叶级数分析方法分为:一重傅立叶变换、二重傅立叶变换以及三重傅立叶变换。结合上节分析,共模电压的谐波展开式与输入频率、输出频率和输出频率均相关。因此假设三变量函数f(x,y,z)在x,y,z方向上均是周期为2π的函数,x,y,z相互独立,则f(x,y,z)的复级数表达式为:

式(16)中k、p、q代表对应变量的系数且为均为整数。
传统双空间矢量调制策略下,TSMC的输出电压与输入电压频率fin、输出电压频率fout以及载波频率fc均相关,故共模电压uNO的谐波频谱也由三种频率的组合决定。令 x=2πfct,y=2πfoutt,z=2πfint,同时将式(16)展开为:

故式(17)代表共模电压中所谐波分量之和,具体每一部分含义如下:第一部分为直流电压分量;第二部分为只与载波频率相关的谐波分量(k=1,2,…;p=0;q=0)、只与输入频率相关的谐波分量(k=0,p=0,q=1,2,3,…)、基波分量(k=0,p=1,q=0)和只与输出频率相关的谐波分量(k=0,p=2,3…,q=0);第三部分为与三个频率中的两个相关的的谐波分量,其频率为任意两种频率整数倍的代数和;第四部分为与三个频率都相关的谐波分量,其频率为三种频率整数倍的代数和。
式(17)中Akpq和Bkpq为:
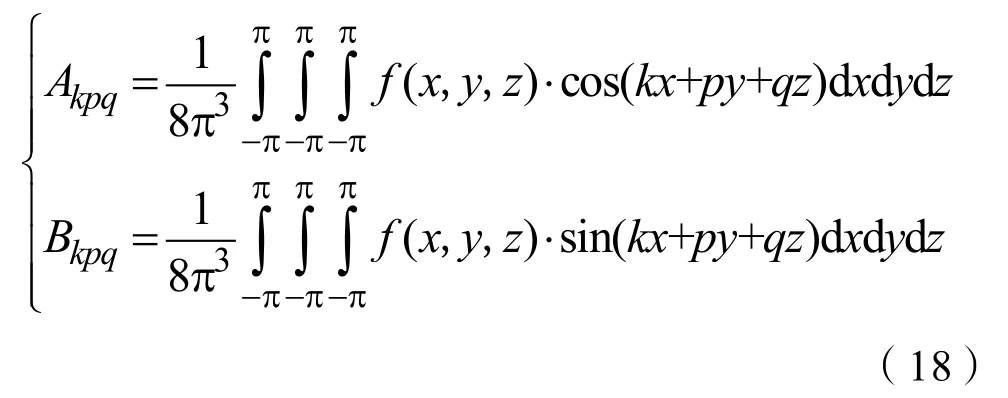
故三重傅立叶系数Fkpq为:
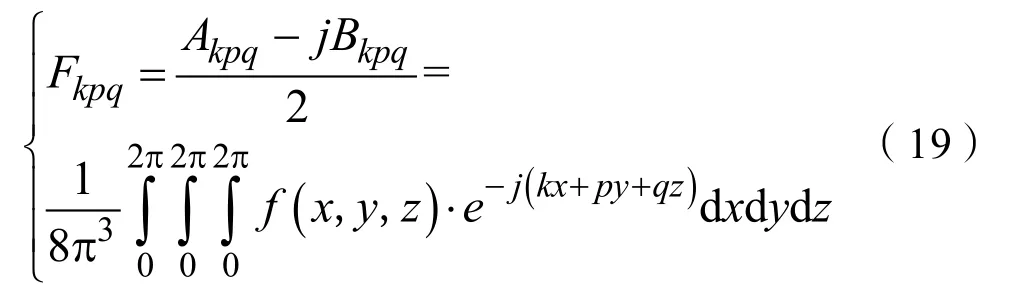
而共模电压展开式中各次谐波幅值 uNO_kpq与三重傅立叶系数之间的关系为:

故通过计算三重傅立叶系数可以得到输出电压中所有的谐波,准确量化输出电压中各种谐波与载波频率、输出电压频率、输入电压频率的关系。
3.2 计算双空间矢量调制下的共模电压谐波幅值
在传统双空间矢量调制策略下,载波选择等腰三角波,记为:
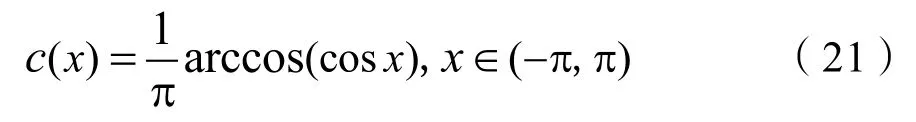
共模电压对应的三重傅立叶系数Fkpq_CMV为:

式(22)中,zx、zs和 yx、ys的取值范围如表 1、2所示。

表1 zx、zs的取值范围Tab.1 V alue range of zx and zs

表2 yx、ys的取值范围Tab.2 V alue range of yx and ys
为了计算三重傅立叶系数,需要先确定共模电压脉冲的跳变时刻,故当整流级和逆变级均处于第I扇区时,逆变级输出的共模电压与脉冲跳变时刻的关系如图5所示。
在图 5中,α1~α6代表逆变级开关的跳变时刻,即当载波大于调制波时,Si1、Si3、Si5为1,而 Si2、Si4、Si6为 0,反之则相反。则各个开关跳变时刻为:
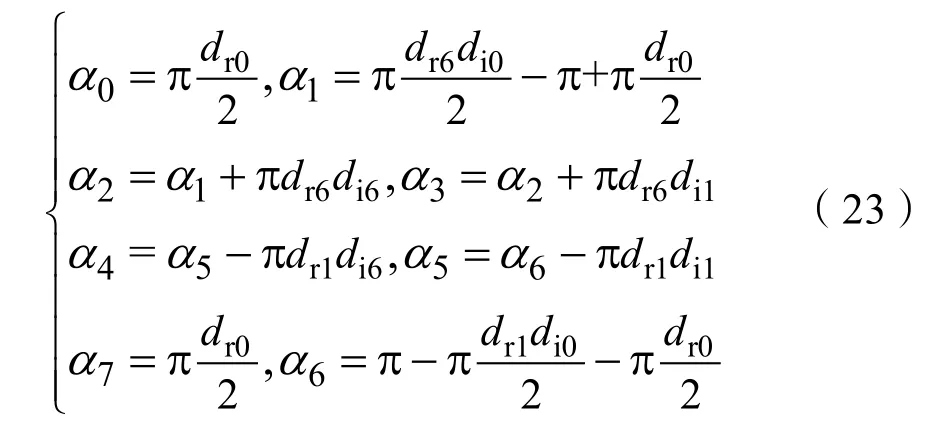
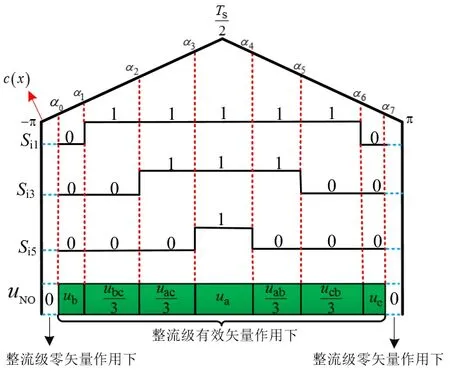
图5 双SVPWM策略下的共模电压Fig.5 Common mode voltage under dual SVPWM strategy
在图5中,为了方便后续计算,每段占空比对应的共模电压化简为余弦函数形式,即:
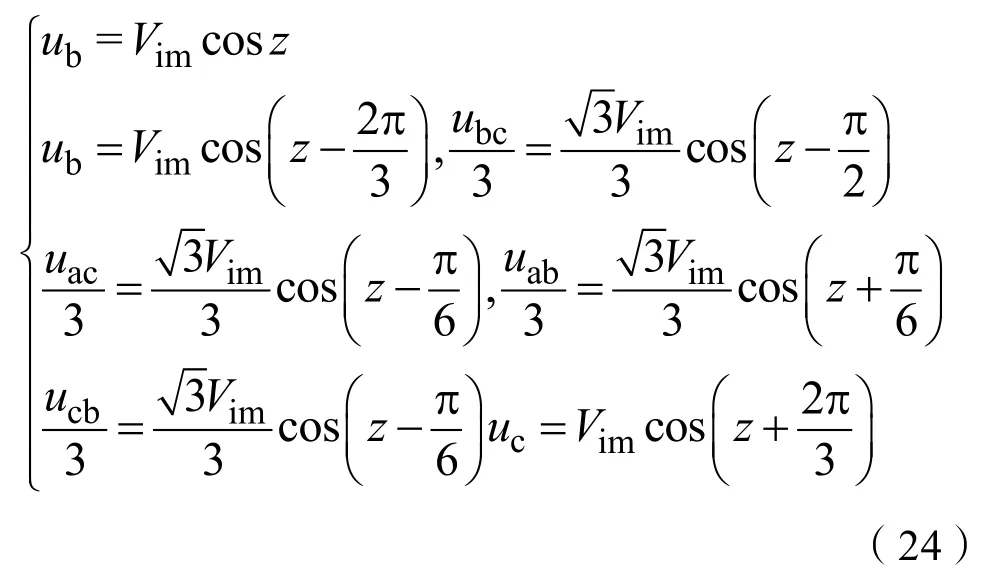
故整流级和逆变级均处于第I扇区时,对应的三重傅立叶系数Fkpq_CMV为:
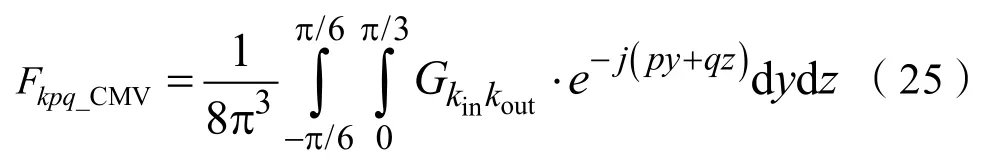
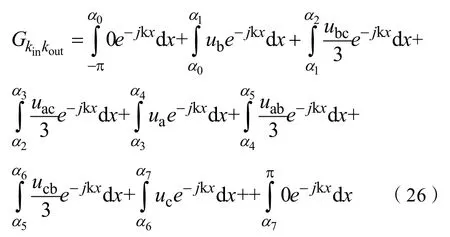
定义下述贝塞尔函数为:
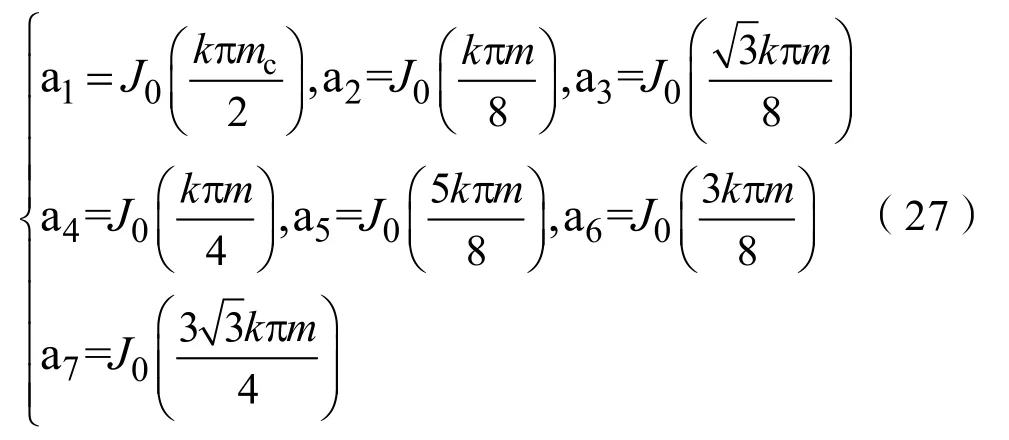
式(27)中,m为两级协调控制后总调制系数,对应的贝塞尔函数值根据m、mc和k的不同取值而变化。进一步利用雅克比-安格尔恒等式、欧拉公式、以及贝塞尔函数积分性质可以得到第 I扇区内共模电压对应的三重傅立叶系数,化简可得:
(1)当k不等于0,p=0,q=1时,对应谐波的三重傅立叶系数Fkpq_CMV为:
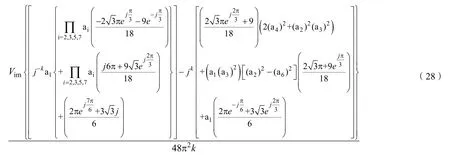
(2)当k不等于0,p=0,q=–1时,对应谐波的三重傅立叶系数Fkpq_CMV为:
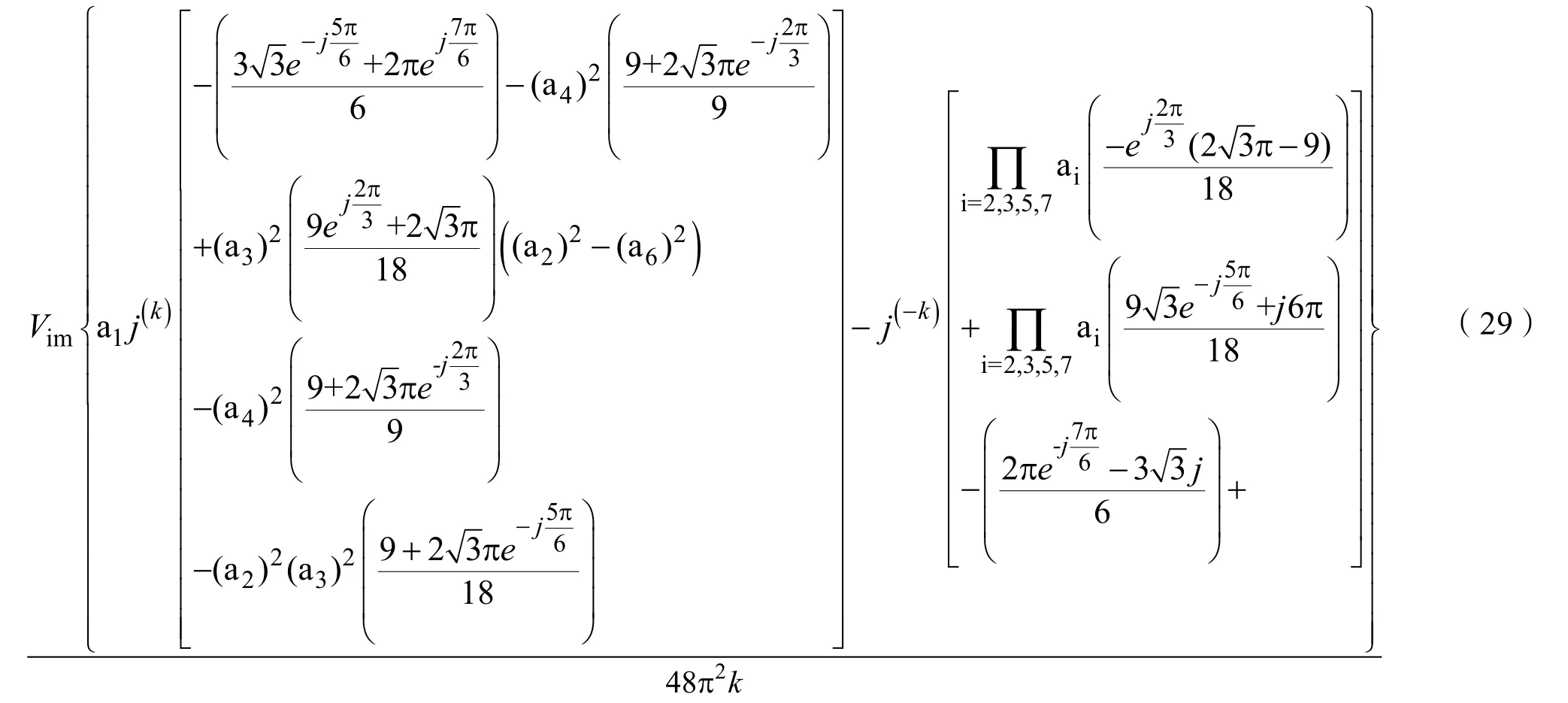
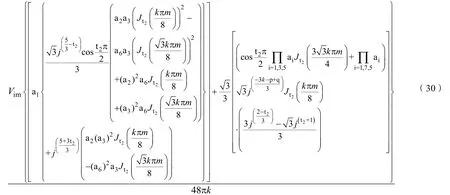
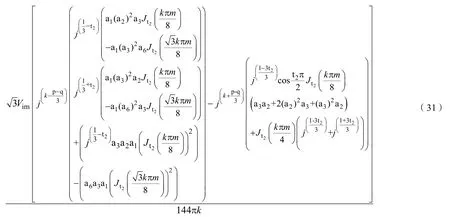
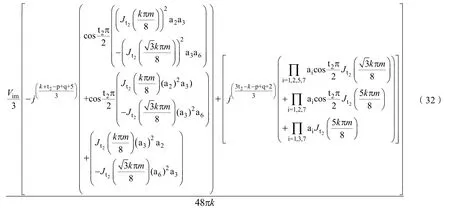
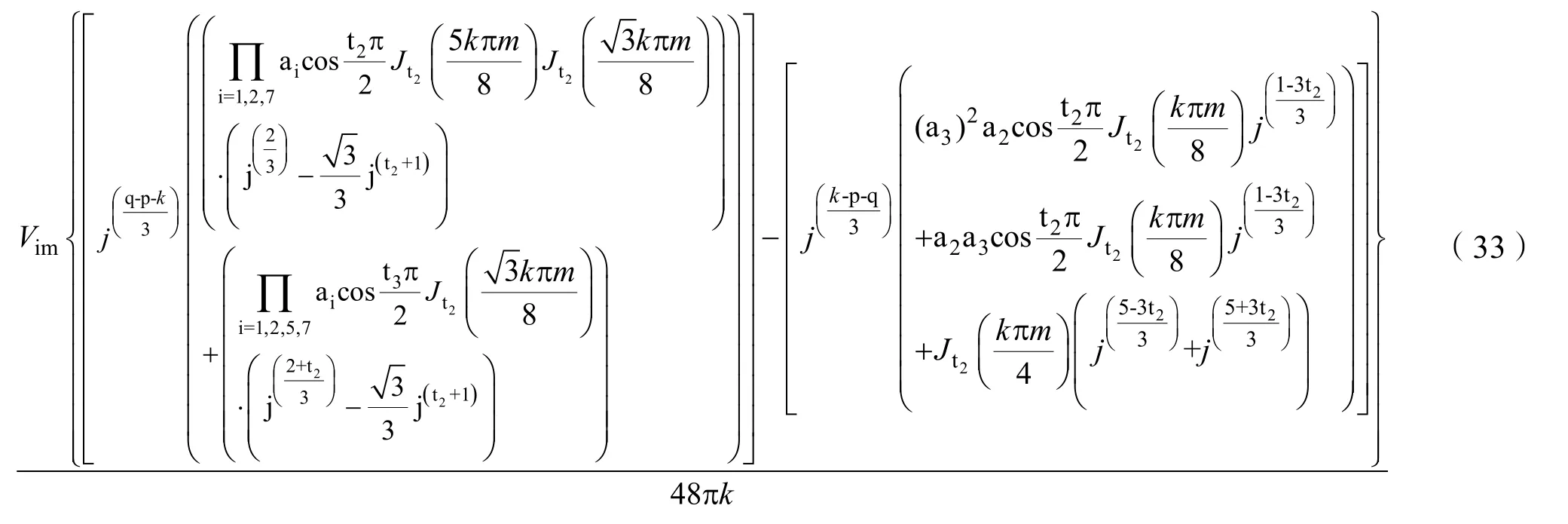
(7)当 k、p不等于 0,q=–1时,对应谐波的三重傅立叶系数Fkpq_CMV为:
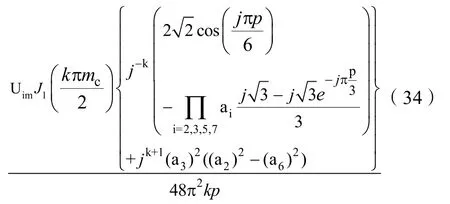
当p、q等于其它值时,对应的三重傅立叶系数为 Fkpq_CMV为零。因此式(28)~(34)表示 Jn(·)阶第一类贝塞尔函数,可通过Matlab计算得出。结合式(18)就可以得到各次谐波详细的解析解。
4 仿真结果分析
为了验证上述理论推导的正确性,利用Matlab仿真软件构建传统双空间矢量调制下TSMC单输出阻感负载仿真模型。由于输入频率为工频值且无法进行改变,同时载波频率一般不作为变量,故对输出频率 fout取整数和非整数两种情况来进行对比。系统的仿真参数设置如表3所示。
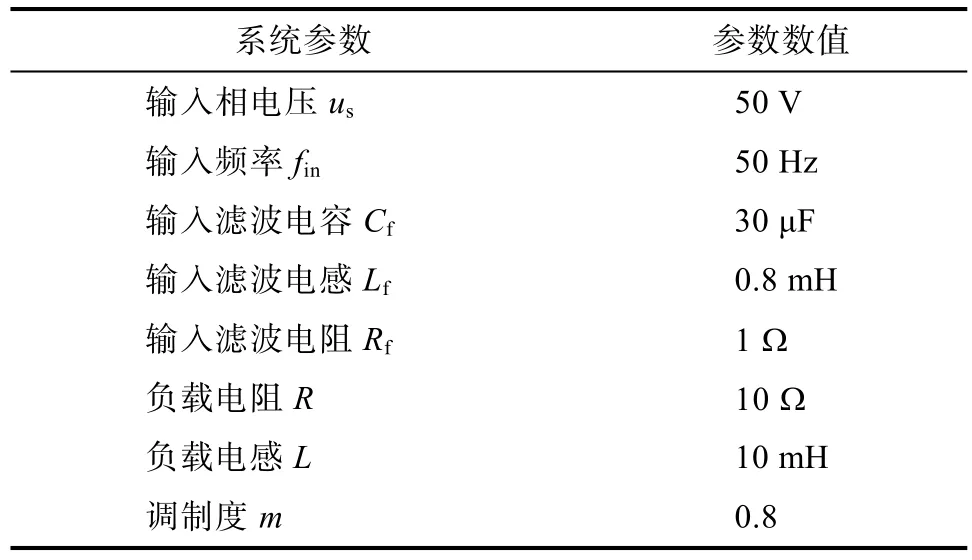
表3 TSMC 系统仿真参数设置Tab.3 Setting of simulation parameters of TSMC system
当输出频率fout取整数时,对应的波形如图6所示。
通过放大图 6(d)得到主要谐波分布的仿真值,且观察图7发现每个仿真值对应一个三种频率组合之后的最终频率,将其带入前面计算得到的各次谐波的最终表达式的限制条件,从而得到最终的的k、p、q关系,再将三种频率对应的倍数关系到对应的三重傅立叶系数表达式,最终得到与FFT分析相同规律的谐波含量值。比较总结如表4所示,所有谐波幅值均为以基波幅值为基准的标么值。

表4 当fout=50 Hz时,共模电压主要谐波分布Tab.4 W hen fout=50 Hz,the main harmonic distribution of common-mode voltage

图6 当fout=50 Hz,输出三相电流、共模电压、线电压的波形和FFT下共模电压对应的谐波频谱Fig.6 When fout=50 Hz,output the waveforms of three-phase current,common mode voltage,line voltage and the corresponding harmonic spectrum of common mode voltage under FFT
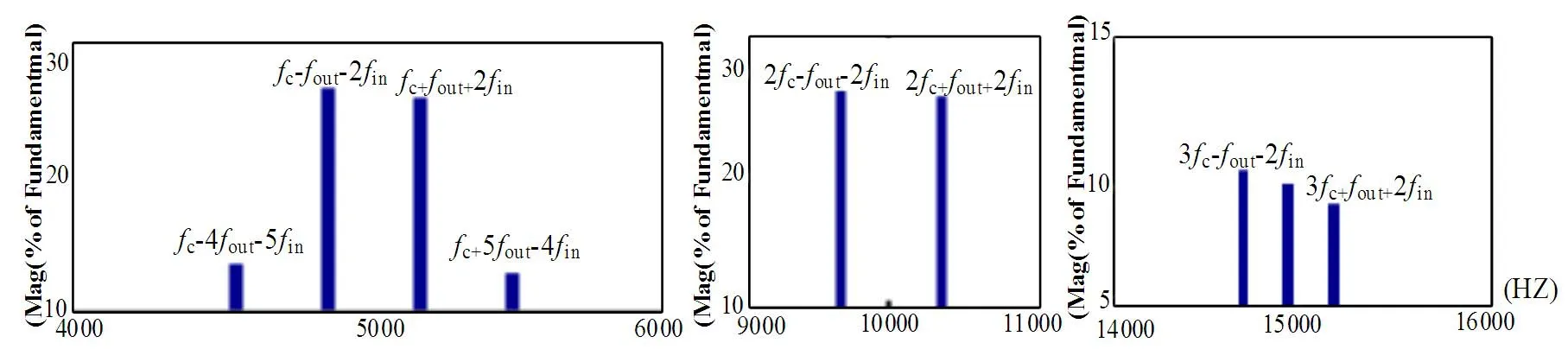
图7 当fout=50 Hz时,FFT下主要谐波分布规律Fig.7 W hen fout=50 Hz,the main harmonic distribution law under FFT
通过表4可以发现,本文所提出的三重傅立叶变换计算方法得到的各种谐波理论值与通过仿真模型FFT分析得到的仿真值接近,故证明了在三种频率组合规律相同的前提下,本文所提方法的正确性和可行性。
为了验证三重傅里叶变换算法的优越性,保证调制比、输入电压频率和载波频率不变,而输出电压频率不为整数时,即fout=50.5 Hz,对应的波形如图8所示。
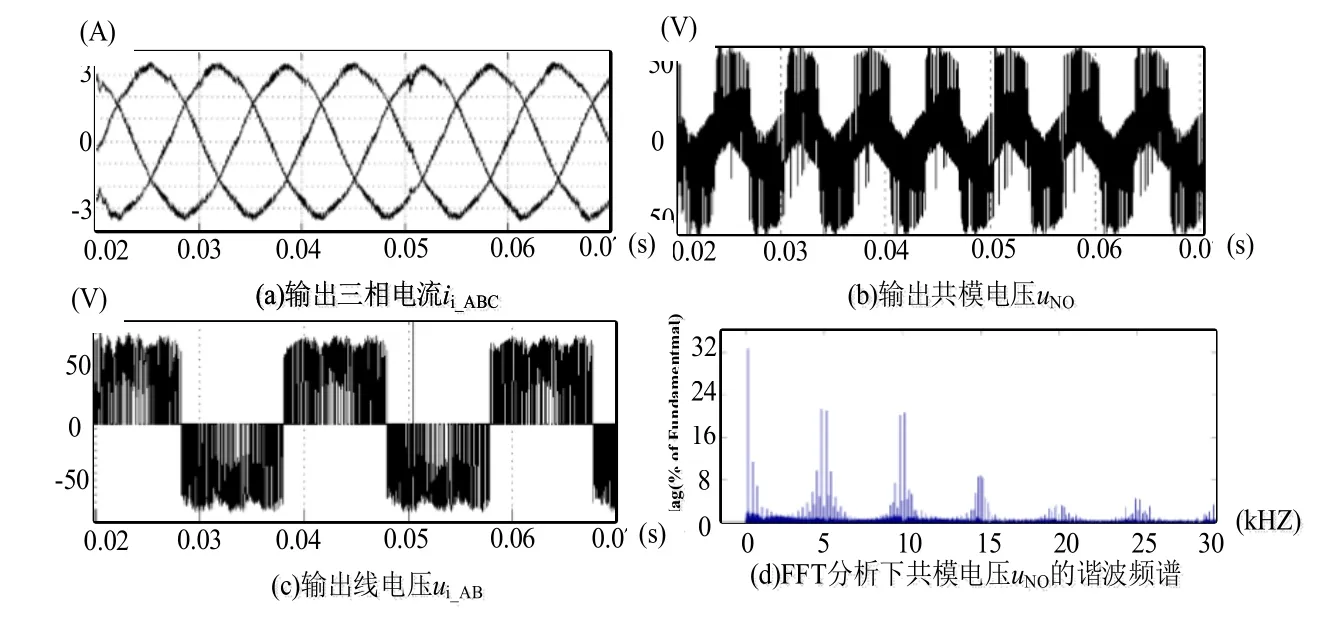
图8 当fout=50.5 Hz,输出三相电流、共模电压、线电压的波形和FFT下共模电压对应的谐波频谱Fig.8 When fout=50.5 Hz,output the waveforms of three-phase current,common mode voltage,line voltage and the corresponding harmonic spectrum of common mode voltage under FFT
通过图9得到对应的主要谐波分布,总结如表5所示。
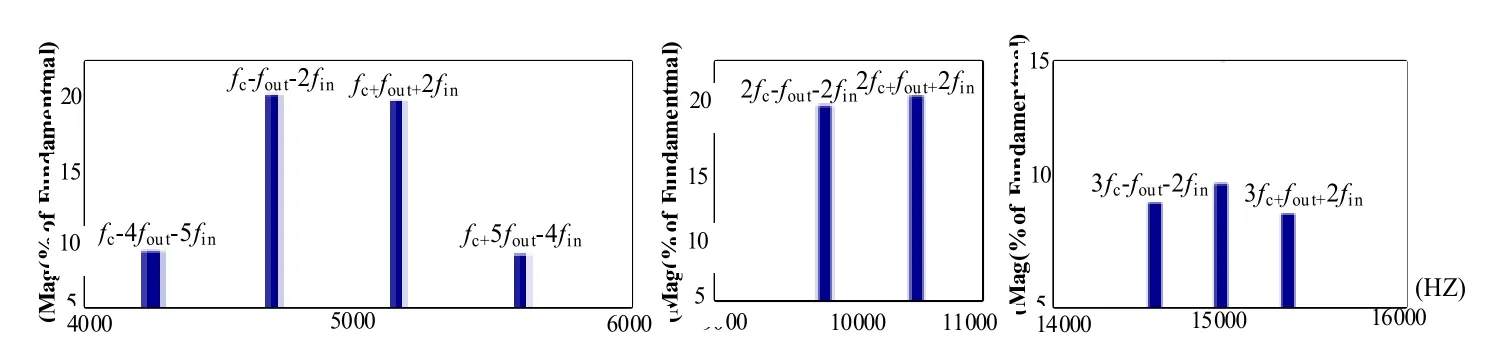
图9 当fout=50.5 Hz时,FFT下主要谐波分布规律Fig.9 When fout=50.5 Hz,the main harmonic distribution law under FFT
通过表5以及对比表4可以看出,以输出频率为4.8495 kHz为例,当输出频率取小数且共模电压的谐波为 fc–fout–2fin时,基于三重傅立叶变换得到的谐波幅值为29.549,相比于输出频率取整数时的理论值29.85变化不大;而通过FFT分析得到的仿真值为21.625,相比于输出频率取整数时的理论值29.31变化较大,其它输出电流谐波规律蕾丝,故证明了本文所提算法优越性。
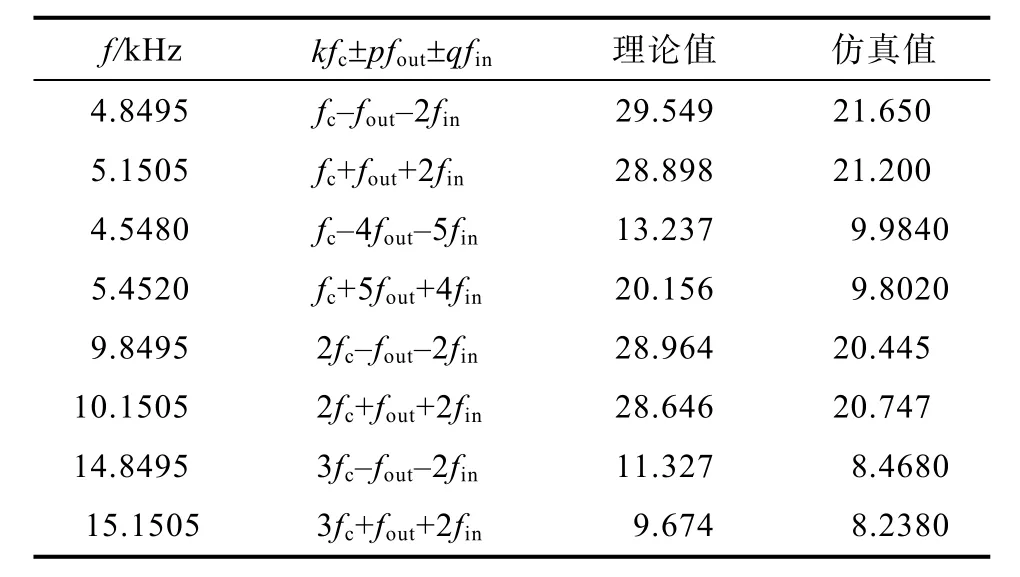
表5 当fout=50.5时,共模电压主要谐波分布Tab.5 When fout=50.5 Hz,the main harmonic distribution of common-mode voltage
5 结论
本文提出在三重傅立叶变换原理的基础上,计算传统双空间矢量调制策略下 TSMC的共模电压全部谐波的解析解,通过仿真及计算结果对比发现:
(1)通过表4可以看出,基于三重傅立叶变换计算得到主要谐波对应幅值与通过 FFT分析得到的各次谐波幅值接近,因此证明了理论计算结果的正确性。
(2)通过表5和表4对比可以看出,当输出频率出现小数时,基于三重傅立叶变换计算得到的谐波幅值主要谐波幅值变化误差在允许的范围内,得到的谐波幅值更准确,而FFT得到的谐波幅值已经出现较大误差。
综上,基于三重傅立叶变换算法的不受频率变化的影响,得到的共模电压谐波频谱不仅全面考虑了三种频率,而且当输出频率 fout取特殊值时依然可以得到较为精准的谐波分布规律,故本文所提方法对于完善共模电压谐波分析理论具有积极意义。
