一种具有单连续变量的背包问题的新V型转换函数二进制粒子群算法求解方法
2021-07-23王泽昆
王泽昆
(河北地质大学 信息工程学院,河北 石家庄 050031)
0 引言
粒子群优化算法(PSO)[1]是1995年由Kennedy和Eberhart提出的一种著名群智能算法。该算法具有参数少,易实现和结构简单等优点,备受广大专家学者的关注。已经在神经网络[2]、约束优化[3]、调度问题[4]等众多问题中得到了成功应用。为了使 PSO算法能够求解离散组合优化问题,Kennedy和Eberhart[5]于 1997年提出了二进制粒子群优化算法(BPSO)。在BPSO中,利用Sigmoid转换函数将由实向量表示的粒子速度转换为由0-1向量表示的粒子位置,从而基于粒子速度实现对粒子位置的更新,可以说 Sigmoid转换函数是BPSO的设计与实现的关键所在[6]。
具有单连续变量的背包问题(KPC)[7]是1999年由Marchand和Wolsey提出的一个带有连续变量S的组合优化问题。目前,国内外学者对KPC的求解算法进行了研究,Lin等[8]首先将 KPC转化为一个伪背包问题和标准 0-1背包问题的组合形式,然后分别利用动态规划算法和分支定界法进行求解。He等[9]首先利用放缩法将 KPC中的连续变量离散化,将它转化为带有实函数的变载重背包问题的一个特例,然后基于动态规划法提出了一个精确算法DP-KPC。Zhao和Li[10]将KPC分解为两个具有标准 0-1背包问题形式的子问题进行求解,提出了一个时间复杂度为 O(n2)的 2-近似算法。最近,He等[11]提出了基于演化算法求解 KPC的新思路,首先基于降维法建立了 KPC的一个适于串行计算的数学模型和一个适用于并行求解的数学模型,然后基于混合编码二进制差分演化算法(HBDE)[12]给出了求解KPC的两个高效离散演化算法,具有混合编码的单种群二进制差分演化算法(S-HBDE)和具有混合编码的双种群二进制差分演化算法(B-HBDE)。显然,求解KPC的已有算法分为两类:精确算法和非精确算法。文献[8-9]中的精确算法具有伪多项式时间复杂度,不适用于求解大规模KPC实例。文献[10-11]中非精确算法特别是演化算法不仅求解 KPC的速度快,而且计算结果完全能够满足实际应用要求,因此探讨利用演化算法求解KPC的高效方法是一个值得研究与探讨的问题。
本文在已有的转换函数的基础上,通过进一步的变形,提出了一个新颖S型转换函数,并基于这一转换函数给出一个新颖的二进制粒子群优化算法(NVBPSO)。为了验证 NVBPSO算法的性能,通过与文献[11]中的算法S-HBDE、B-HBDE和 BPSO求解4类 KPC实例的计算结果进行比较,根据比较结果指出NVBPSO在求解KPC时比其他算法所具有更大的优越性能。
1 KPC 的定义和数学模型
KPC的定义为:给定 n个物品的集合 N={1,2,…,n}和一个基本载重为C的背包。其中物品j∈N具有价值pj和重量wj,背包的可变载重S∈[l,u]。pj,wj和 C为正有理数,S,l和 u为有理数,且l<0
根据上述定义,KPC的基本数学模型KPCM1[11]描述如下:
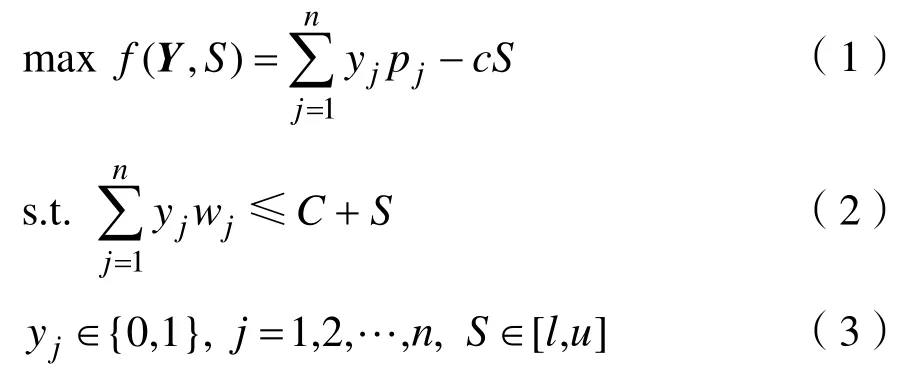
其中,Y=[y1,y2,…,yn]∈{0,1}n,yj=1(j=1,2,…,n)表示物品 j被装入了背包中。为了便于利用二进制演化算法求解KPC问题,文献[11]基于降维法建立了KPC的一个新数学模型KPCM2,该模型通过消去连续变量S使解空间的维数由n+1降低为n。数学模型KPCM2的描述如下:
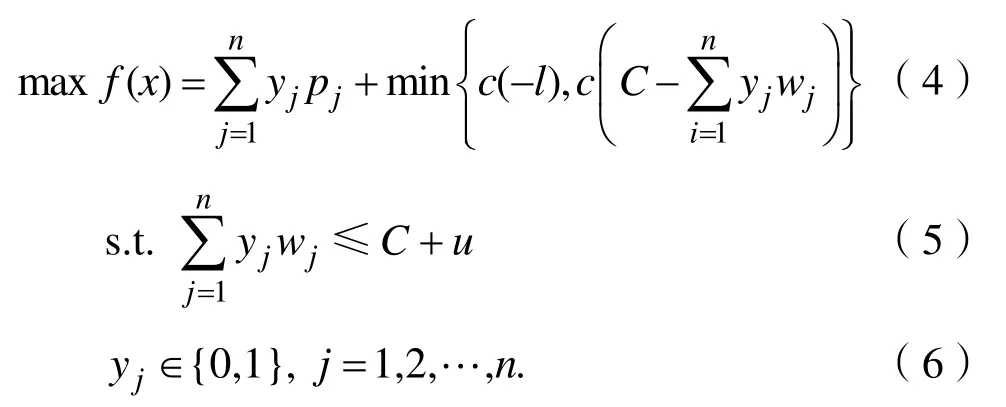
2 BPSO和NVPSO
2.1 BPSO
PSO算法受鸟群飞行觅食的行为而产生灵感,协作来寻找最优解的进化计算技术。PSO主要包含粒子的速度更新(如式(7))和位置更新(如式(8))两个重要操作。
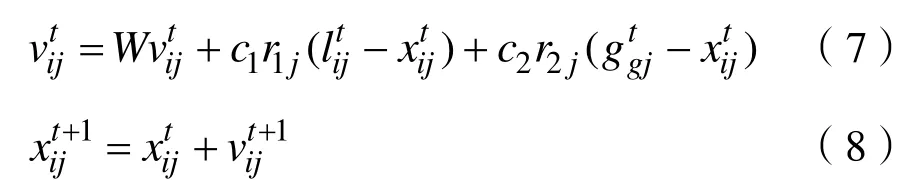
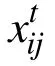
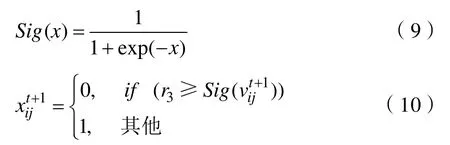
其中,r3为0~1之间的随机数。
2.2 NVBPSO
近年来,转换函数成为二进制演化算法研究的热点问题。目前,已有的转换函数可以分为两类:S型传递函数和 V型传递函数[13-14]。在表 1中分别给出了4个S型转换函数(记为S1-S4)和4个V型转换函数(记为V1-V4)。

表1 S型转换函数和V型转换函数Tab.1 S-shape and V-shape transfer functions
本文为了兼具S型和V型转换函数的特性,基于S2转换函数提出了一个新V型转换函数NV:

3 利用NVBPSO求解KPC
3.1 NVBPSO
Lee等[15]改进了BPSO,他们在保持PSO的速度更新公式和位置更新公式的基础上,利用位置值的概率对粒子的位置进行第二次更新操作。基于这一方法,并结合所给出的新V型转换函数NV,提出了一个新的二进制粒子群优化算法NVBPSO。
在NBPSO的进化过程中,首先利用式(7)更新粒子的速度,接着利用式(8)对粒子位置进行第一次更新。然后,利用第一次位置更新后的位置值根据式(12)来计算粒子位置向量变化的概率值。
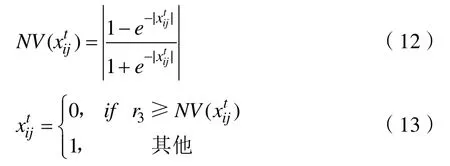
最后,根据求得的粒子位置向量变化的概率值,利用式(13)对粒子进行第二次位置更新。
3.2 利用NVBPSO求解KPC
在利用NVBPSO求解KPC问题时,不可行解的产生是不可避免的。为了解决这一问题,文献[11]给出了一种时间复杂度为O(n2)的修复与优化算法M2-GROA来处理KPC的不可行解。由于M2-GROA在文献[11]中的成功的应用,本文利用M2-GROA处理NBPSO在求解KPC时所产生的不可行解。
设Yb∈[0,1]n表示求得KPC实例的当前最优解。f(Yb)表示Yb所对应的适应度值。基于NBPSO求解KPC的算法的步骤如下。
基于NBPSO求解KPC的步骤:
Step.1将n个物品项利用Quicksort[16]按照物品的价值密度比降序排序,并将排序后的物品项的下标依次存入一维数组H[1,2,…,n]中;
Step.2初始化参数。设置最大迭代次数MIter,种群规模N,惯性参数W,加速系数c1,c2和vmax;令 t←0。
Step.3随机初始化种群。使粒子位置的每一分量随机取 0或 1,粒子速度的每一分量在[-vmax,vmax]内随机取值。
Step.4 利用M2-GROA处理初始化时产生的不可行解,并计算粒子的适应度值;
Step.5对于所有粒子,分别利用式(7)和式(8)更新它的速度和位置;
Step.6 利用式(12)计算改变粒子位置向量的概率;
Step.7利用式(13)中二次更新粒子的位置向量;
Step.8利用 M2-GROA处理粒子更新后所产生的不可行解,并计算它的适应度值。
Step.9判断是否满足终止条件。若不满足,则t←t+1,转Step.5;若满足,则输出(Yb,f(Yb))。
在上述步骤中,Step.1利用快速排序QuickSort[16]实现,其时间复杂度为 O(nlogn);Step.3的时间复杂度为O(N×n);Step.4的时间复杂度为O(N×n2);Step.4~9的时间复杂度为 O(MIter×N×n2);因此NBPSO求解 KPC的时间复杂度为 O(nlogn)+O(N×n)+O(N×n2)+O(MIter×N×n2),其中 MIter 和N是关于n的多项式,故为多项式时间复杂度。
4 计算结果与分析
所有计算均在配置为Inter(R)Corei7-3770 CPU@3.40 GHz和8 GB RAM的微型计算机上进行。利用C语言进行编程,编译环境为Code:Blocks。使用Python在编译环境JetBrains PyCharm下绘制折线图。
4.1 四类KPC实例
四类不同的KPC实例为ukpc类、ikpc类、wkpc类和 skpc类,编号为 ukpc100-ukpc1000,ikpc100-ikpc1000,wkpc100-wkpc1000,skpc100-skpc1000。所有KPC实例的具体数据都来自URL https://www.researchgate.net/project/KPC-problemand-Its-algorithms
4.2 计算结果比较与分析
在 NVBPSO算法中,设置种群规模均为N=20,最大迭代次数均为MIter=6n,n为KPC实例中物品的个数;此外,惯性参数 W=1.5,加速系数c1=c2=1.8,粒子速度向量中各维分量的取值范围为[-2,2]。S-HBDE、B-HBDE和BPSO的种群规模均为N=20,三个算法其他参数与文献[11]中相同。
记OPT是利用文献[9]中方法求得KPC实例的最优值。Best为算法独立计算实例50次所得计算结果中的最好值,Mean和StD分别为50次所得计算结果的平均值和标准差。AR=|OPT-Mean|表示算法求解 KPC实例的计算结果的平均值与最优值之间的绝对误差。在表2~表5中给出了各算法求解四类 KPC实例的计算结果,并根据表2~表5中的计算结果,利用它们比较NVBPSO、S-HBDE、B-HBDE和BPSO算法计算结果的优劣。
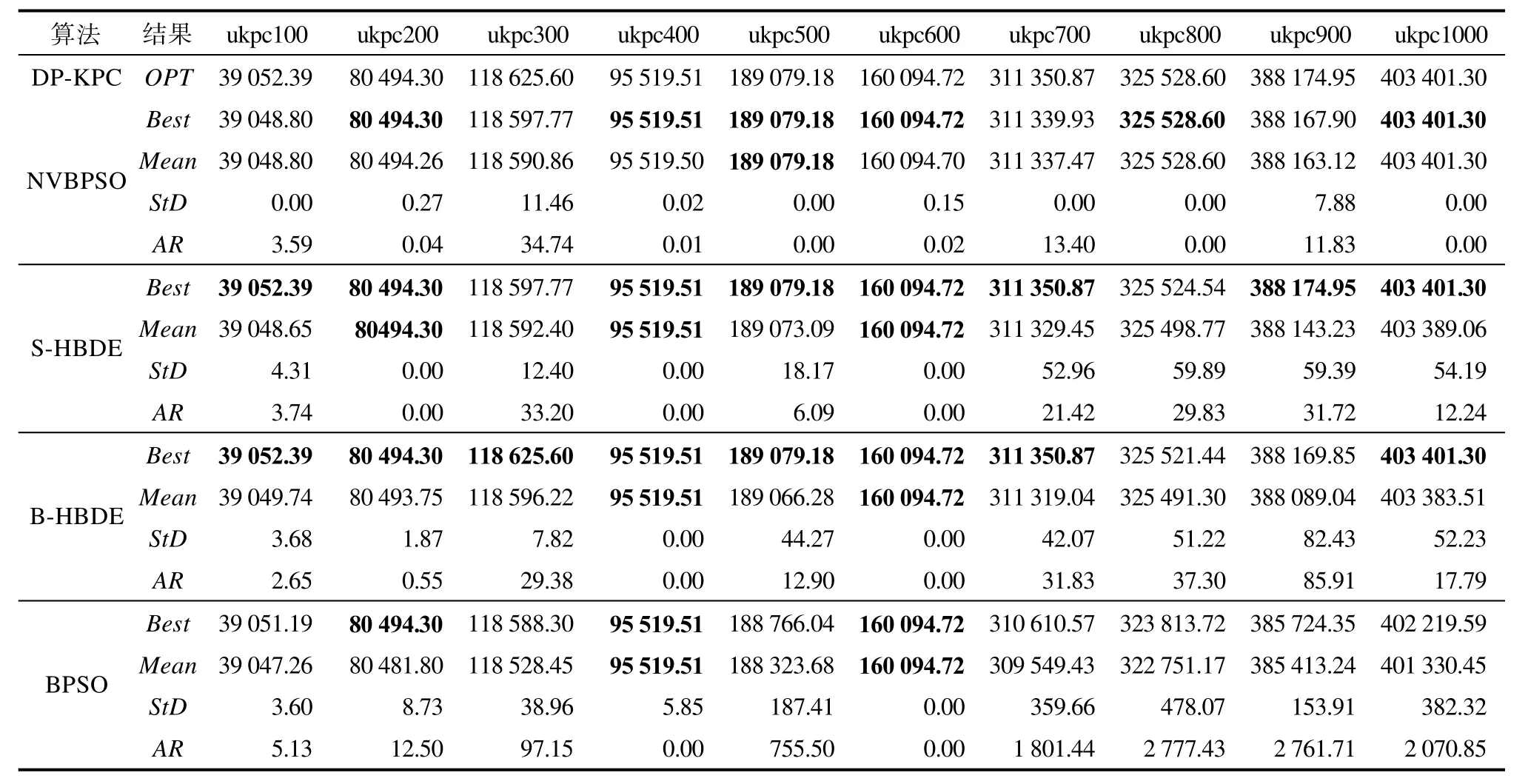
表2 NVBPSO、S-HBDE、B_HBDE和BPSO求解ukpc类实例的计算结果Tab.2 NVBPSO,S-HBDE,B-HBDE and BPSO calculation results of ukpc class instances

表3 NVBPSO、S-HBDE、B_HBDE和BPSO求解ikpc类实例的计算结果Tab.3 NVBPSO,S-HBDE,B-HBDE and BPSO calculation results of ikpc class instances
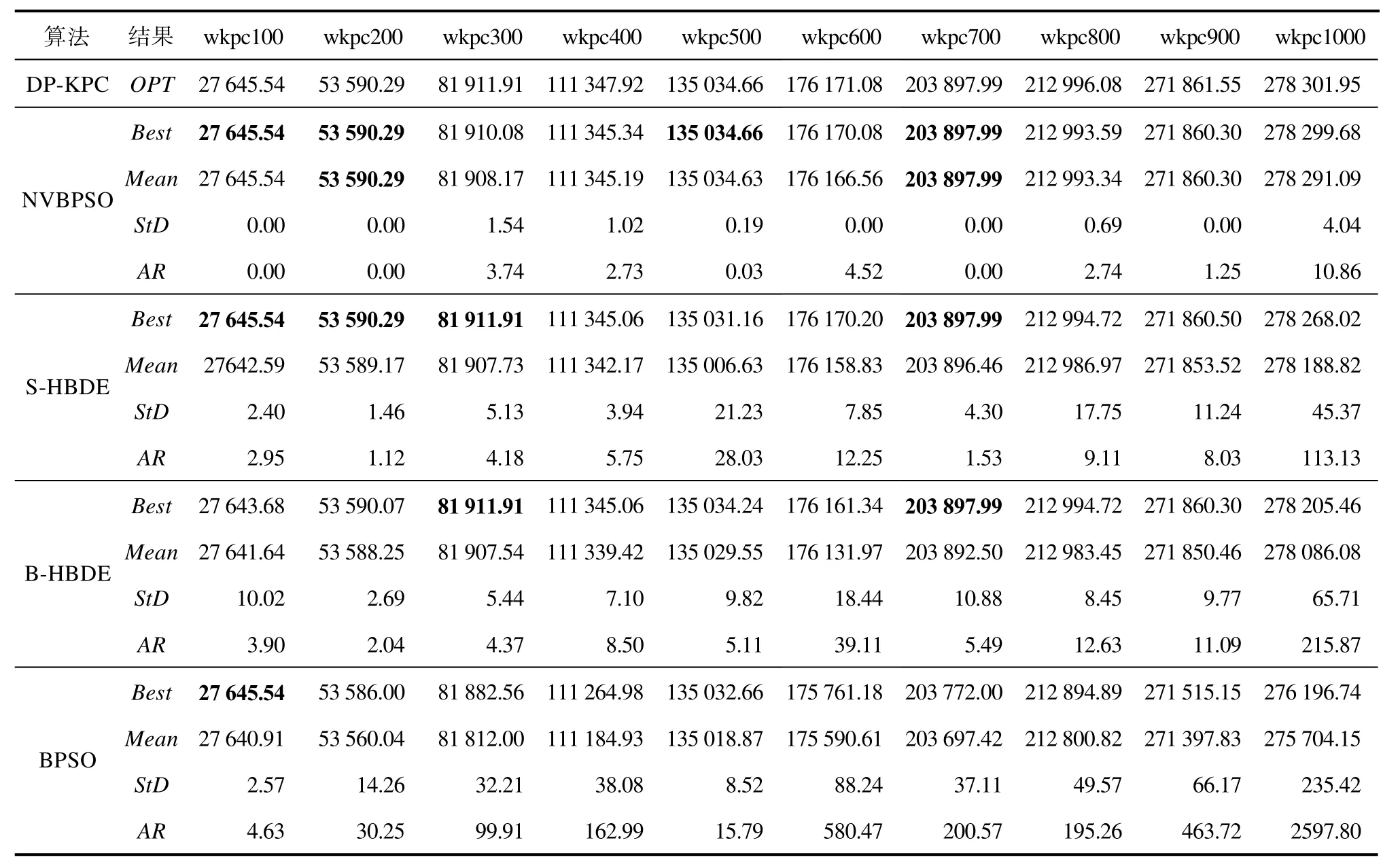
表4 NVBPSO、S-HBDE、B_HBDE和BPSO求解wkpc类实例的计算结果Tab.4 NVBPSO,S-HBDE,B-HBDE and BPSO calculation results of wkpc class instances
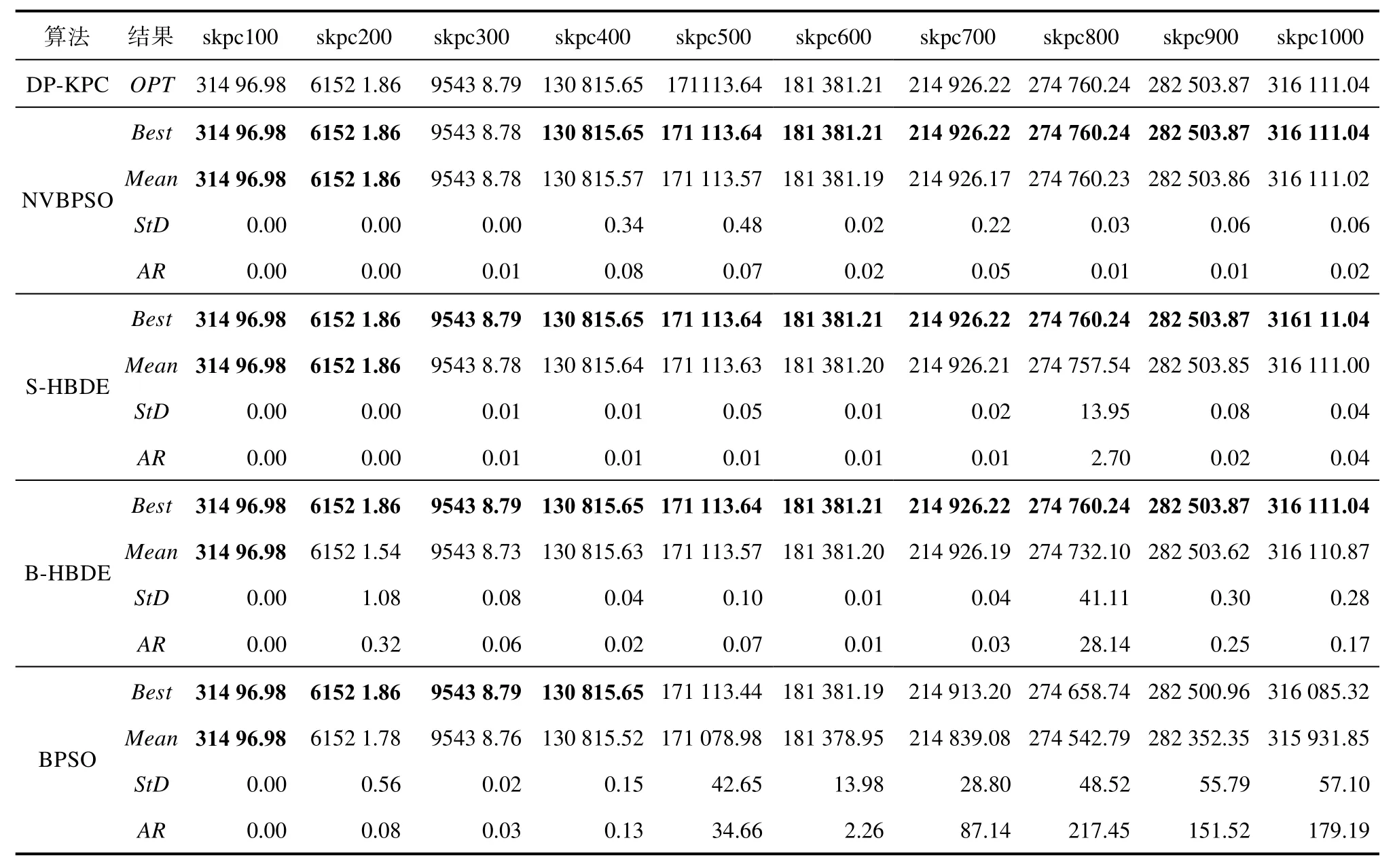
表5 NVBPSO、S-HBDE、B_HBDE和BPSO求解skpc类实例的计算结果Tab.5 NVBPSO,S-HBDE,B-HBDE and BPSO calculation results of skpc class instances
由表2可以看出,对于ukpc类实例NVBPSO在求解ukpc100、ukpc500、ukpc700-ukpc1000实例时,虽然部分Best值未达到OPT值,但是Mean值相对于其他三个算法均有较大的提高。从表 3可以看出,对于 ikpc类实例 NVBPSO在求解ikpc300-ikpc1000实例时,在大部分 Best值达到OPT值的基础上,取得的Mean值均优于其它三个算法。从表4可以看出,NVBPSO在求解wkpc类实例时取得的 Mean值其它三个算法。从表 5可以看出,NVBPSO在求解 skpc类实例,除skpc300实例外,其他实例取得的 Best值均达到OPT值且大部分实例的Mean值均优于其它三个算法。由于在评价演化算法时,指标 Mean比指标Best更能说明问题演化算法的性能优劣,因此NVBPSO相比于S-HBDE、B-HBDE和BPSO求解KPC问题的性能更佳。
5 结论
本文介绍了常见的8个S型和V型转换函数,并受这两类转换函数的启发,提出了一种新V型转换函数NV。在此基础上,给出了一种基于新V型转换函数的二进制粒子群优化化算(NVBPSO)。为了验证NVBPSO的求解性能,本文通过求解4类大规模KPC实例,验证了算法的高效性和有效性,并通过与已有算法的计算结果比较表明:NVBPSO比S-HBDE、B-HBDE和BPSO的求解结果优,算法的鲁棒性更佳,非常适用于求解大规模KPC实例。
通过实验证明,本文所提出的新V型转换函数是可行的,有效的。同时为连续演化算法离散化提供了一种新V型函数。在未来研究中,我们将探索新V型转换函数对其他二进制算法的影响,如灰狼算法(GWO)[17]和鸽群优化算法(PIO)[18]等。此外,我们将继续尝试利用NVBPSO求解其他组合优化问题,例如设施选址问题[19],集合覆盖问题[20]等。
