基于主应力旋转的黏性填土挡墙土压力

王恒利，邹正盛，刘京敏，王新宇

（1.河南理工大学土木工程学院，河南 焦作 454003；2.河南省地下空间开发及诱发灾变防治国际联合实验室，河南 焦作 454003；3.河南省地下工程与灾变防控重点实验室；河南 焦作 454003；4.中国地质工程集团有限公司，北京 100093）

众所周知，挡墙墙背粗糙，黏性土挡墙墙土界面存在一定的摩擦。对于这种情况，经典朗肯土压力理论不再适用。为了使理论计算结果更接近于实际，众多学者探索考虑墙土摩擦作用的土压力计算。

考虑墙土摩擦进行黏性土土压力计算时，大多为基于经典理论的修正方法。早期的方法有：等值内摩擦角法、楔体试算法、内压力法、图解法等[1−3]。后来，一些学者在库伦土压力理论的基础上进行了改进，取得了一系列进展。朱桐浩等[4]在库仑理论平面滑裂面假设条件下，从土体的极限平衡条件出发，由滑动楔体的极限平状态，导出考虑墙土摩擦的黏性土主动土压力计算式。赵恒惠[5]基于库伦土压力理论，将墙土之间摩擦角和墙土之间的黏结力用折减土体内摩擦角和黏结力表示，推导了重力式挡墙土压力计算式。顾慰慈[6]假定滑裂面为平面，导出考虑墙土摩擦的黏性土主动土压力的库仑解。罗绍军[7]基于库伦平面滑裂面假定，考虑滑裂面黏聚力作用，通过力矢多边形，建立了黏性土主动和被动土压力计算式。卢廷浩[8]应用平面滑裂面假定，考虑墙土摩擦及黏结力以及填土表面裂缝和超载的影响，推导了挡墙的主动土压力计算式。李巨文等[9]在文献[5]的基础上，给出了距墙顶一定距离均布荷载作用下的主动土压力计算式。胡晓军[10−11]基于库仑理论的平面滑裂面假设，先后建立了考虑墙土接触面上黏结力与摩擦力作用的主被动土压力计算式。彭明祥[12−13]认为极限土压力是由墙后塑性土体产生，假定塑性区平面滑裂面，建立了考虑墙土摩擦及墙土界面黏结力作用的挡墙土主动土压力计算式。杨敏等[14]基于平面滑裂面假定，结合微分层解析法和图解法，推导了考虑墙土摩擦及黏结力作用的土压力计算公式。曹雄等[15]在文献[8]的基础上，应用力的矢量多边形法推导了考虑墙土摩擦及黏结力作用的主被动土压力计算式。柯才桐等[16]基于库仑土压力理论假设，从滑动楔体极限平衡状态时力的静力平衡条件出发，推导出不同分布模式条形荷载作用下考虑墙土摩擦和墙土之间黏结力的主动土压力计算式；后来，又采用斜向条分法，推导了一般条件下挡墙土压力强度的表达式[17]。胡卫东等[18]基于平面滑裂面假定，对极限平衡状态的墙后土楔体进行静力平衡分析，考虑墙土界面摩擦与黏结力、填土的黏聚力影响，建立了有限土体主动土压力计算方法。陈建功等[19]从墙后滑楔体整体静力平衡方程出发，采用整体极限变分法对土压力进行求解，建立了考虑墙土摩擦的黏性土挡墙土压力计算方法。

事实上，对于朗肯挡墙，当墙背与其后土体之间存在摩擦时，墙后土体会产生非均匀应力场，墙背附近土体由于墙土摩擦产生的剪切力而使土体单元主应力方向发生偏转，而墙背稍远处土中应力场仍符合朗肯土压力条件。针对墙背面土体主应力偏转这一事实，Lancellotta[20]基于塑性下限定理，采用主应力旋转办法，建立了考虑墙土摩擦的土体极限状态下无黏性土挡墙的主被动土压力计算方法；后来，又进一步给出了地震条件下的无黏性土的主被动土压力计算公式[21]。

然而，目前针对黏性土条件下的土压力计算研究较少。本文拟采用主应力旋转处理方法，考虑黏性土中的黏聚力作用，推导考虑墙土摩擦和黏结力作用的黏性土主动土压力和被动土压力的计算公式；同时，将计算结果和现有相关方法进行对比，分析墙土摩擦角和土体内摩擦角对黏性土挡墙土土压力的影响。

1 被动土压力计算解析

对于被动状态的朗肯挡墙，由于墙土摩擦作用，墙后土体将分别处于两种应力状态区域：墙后相对远处土体的大小主应力分别为水平应力和竖向自重应力；近墙土体由于墙土摩擦和黏结力作用，水平应力和竖向自重应力不再是大小主应力，主应力轴向墙外发生一定程度的偏移。无疑，这两种应力状态间存在1条公共线（即界线），如图1所示。

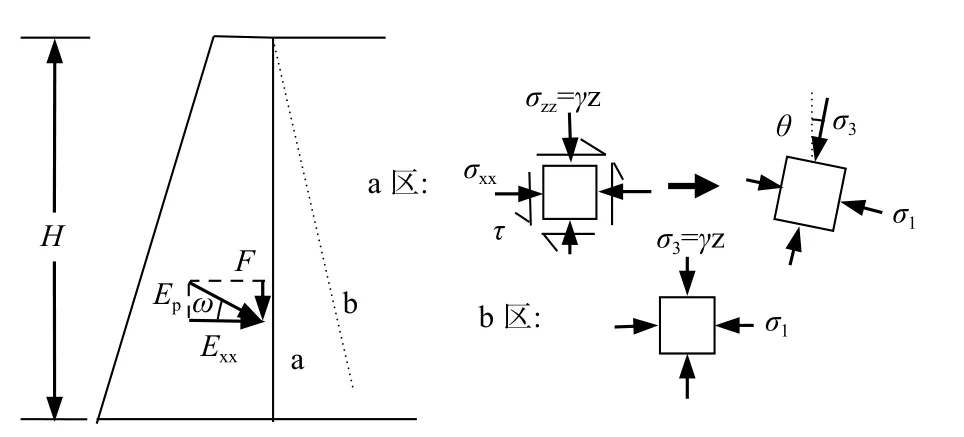
图1 被动极限状态土体单元应力图Fig.1 Stress of soil element under the passive limit state

取墙背和墙后土体单元进行应力分析。对墙后土中两种应力状态进行推算，则在分界线上应力不一致（图2）。图2中，未发生偏转的莫尔圆与包线在T处相切，偏转后的莫尔圆与偏转前的莫尔圆交点为X。对于黏性土，由于黏聚力不为零，可将τ轴左移l（l=ccotφ），得到坐标原点为（0,0）的新坐标系，s'=s+l，σ'xx=σxx+l。通过对三角形ABX应用正弦定理，可以得到：

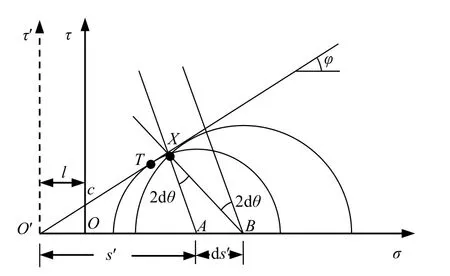
图2 应力圆心偏移图Fig.2 Diagram showing the stress center deviation

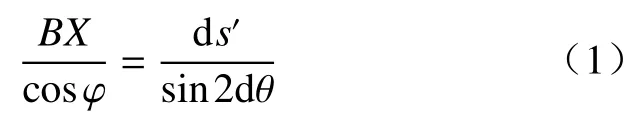
假设应力圆产生1个小转动2dθ。当ds'→0时，sinθ≌θ，公共点X→T，则BX≌AX。此时式（1）变为：

则：

式中：θ—主应力方向的旋转角；

φ—填土内摩擦角；

s'—调整后的莫尔圆圆心横坐标。

绘制被动挡墙墙背及墙后土体摩尔应力圆（图3），其中墙后土体应力圆2主应力方向未发生偏转，圆心横坐标为s′2。假定主应力方向的偏转为有限值θ，得到墙背土体应力圆1，圆1的圆心横坐标为s′1。显然，圆2的偏转角为0，圆1的偏转角为θ。对式（3）积分：

图3 被动土压力应力圆Fig.3 Passive earth pressure stress circle

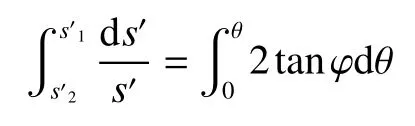
得：

在主应力方向偏转后的应力圆1中（图3）：

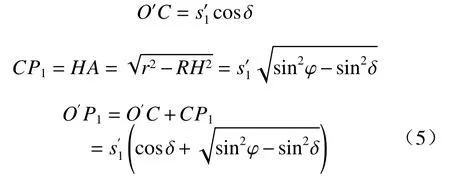
式中：δ—墙背与填土间的摩擦角。

又由于

且圆2之中主应力方向未发生偏转，即：

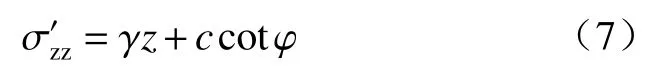
故：

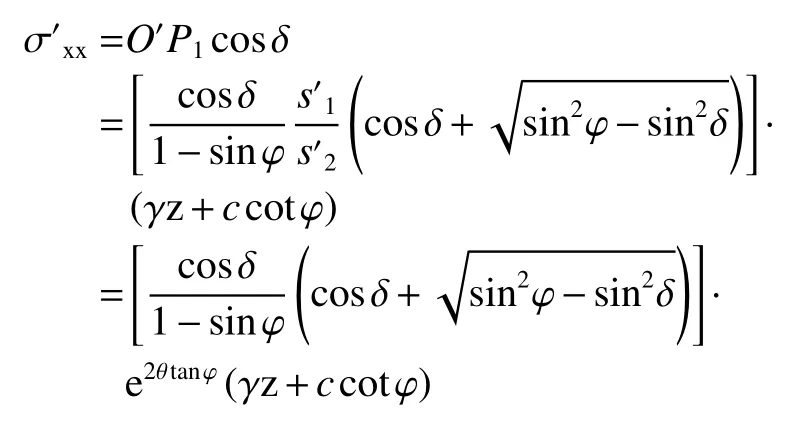
墙背土体单元水平应力为：

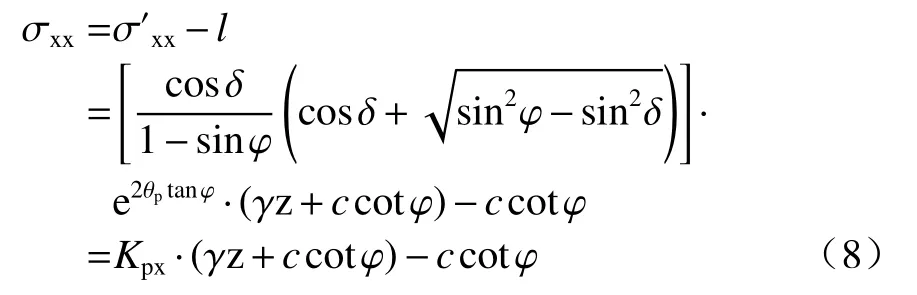
式中：

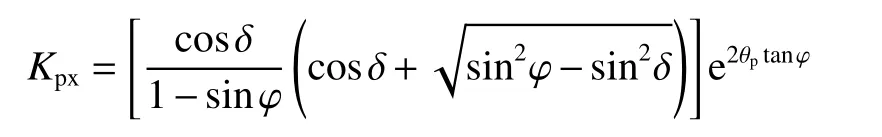
墙背土体单元剪应力：

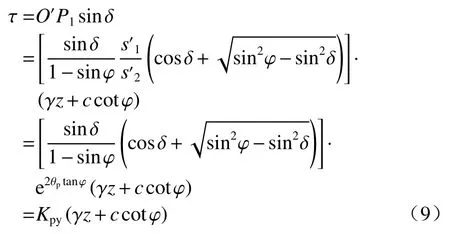
式中：

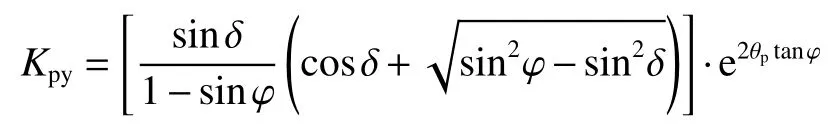
则作用在挡土墙上的被动土压力强度为：

墙背切向力：

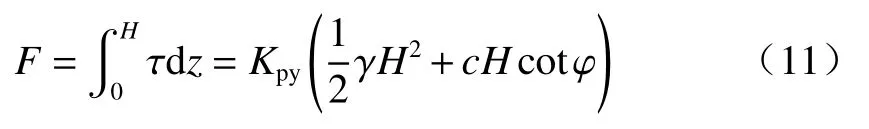
墙背水平力：

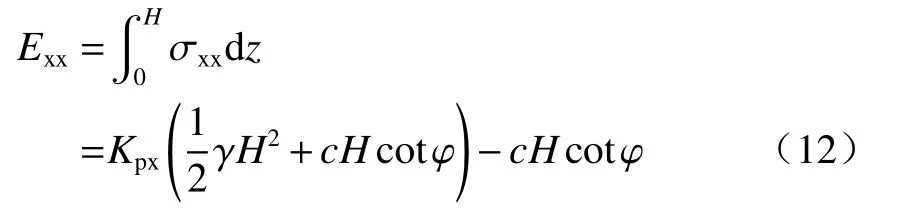
则黏性土挡土墙被动土压力为：

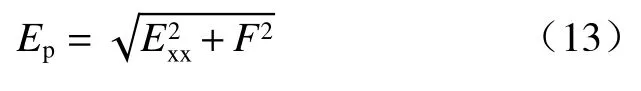
被动土压力与墙背法线之间夹角：

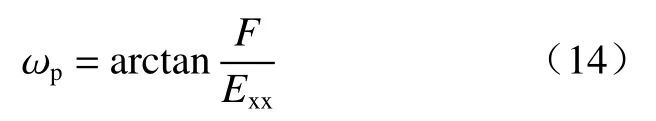
由图3中的圆1，有：

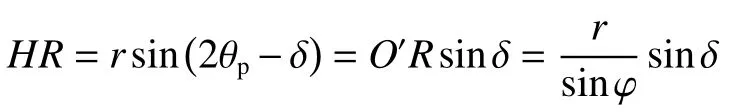
则墙后土体主应力偏转角θp为：

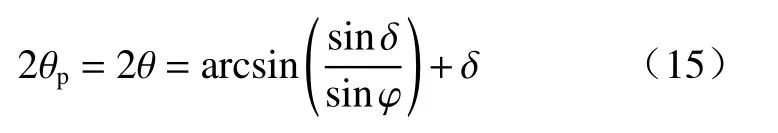
由图3可知，墙土界面黏结力cw与墙土界面摩擦角δ、填土黏聚力c、内摩擦角φ存在如下关系：

若墙背光滑（δ=0），则θp=0，cw=0，式（13）退化为：

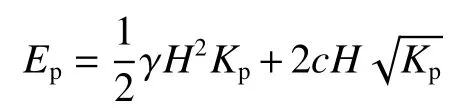
这意味着，若不考虑墙土摩擦角，被动土压力计算式与朗肯被动土压力公式相等。

2 主动土压力计算解析

对于主动土压力情形，墙后土体应力状态如图4所示。同样，取墙背和墙后土体单元进行分析，则主动挡墙墙背及墙后土体摩尔应力圆如图5所示。其中，主动土压力应力圆1为墙后土体单元应力圆，圆心横坐标为s′1，主应力方向未发生偏转。墙背土体应力圆2，主应力方向偏转角为θ。同理有：

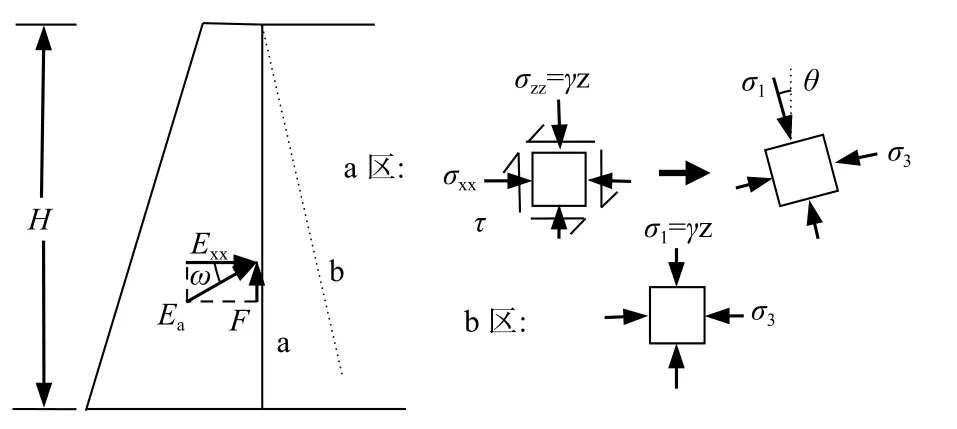
图4 主动极限状态土体单元应力图Fig.4 Stress of soil element under the active limit state

由图5可得：

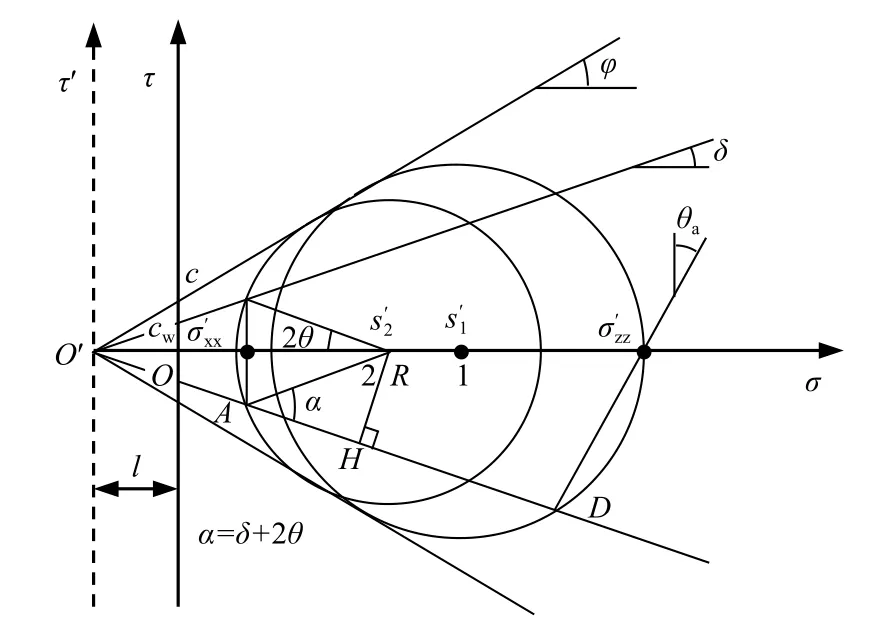
图5 主动土压力应力圆Fig.5 Active earth pressure stress circle

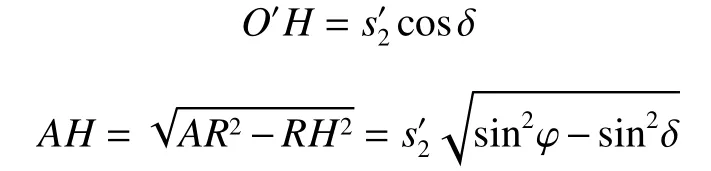
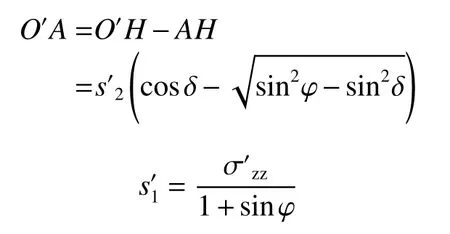
由于圆1之中主应力方向未发生偏转，则：

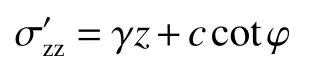
可得：

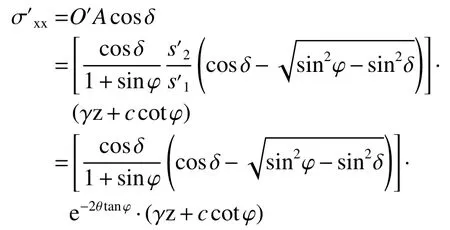
墙背土体单元水平应力：

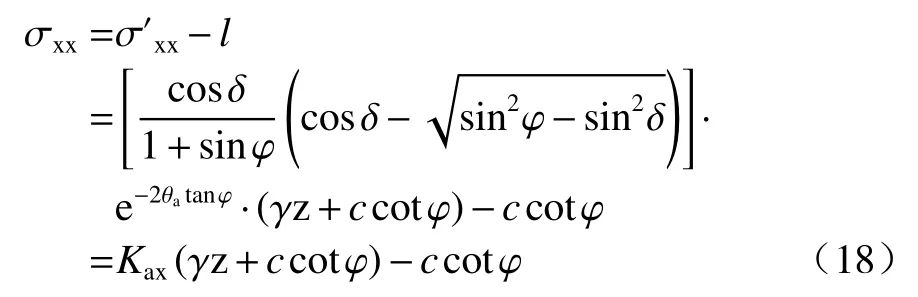
其中：

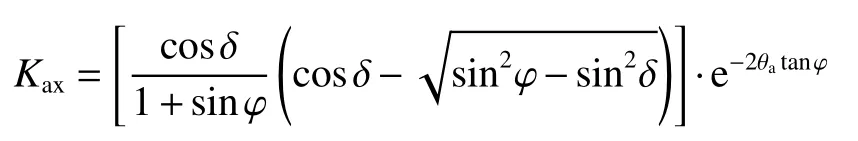
墙背土体单元剪应力：

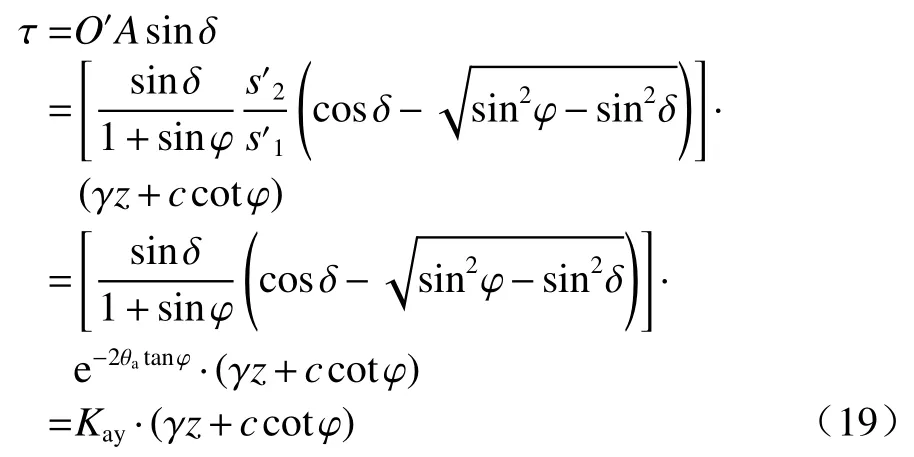
式中：

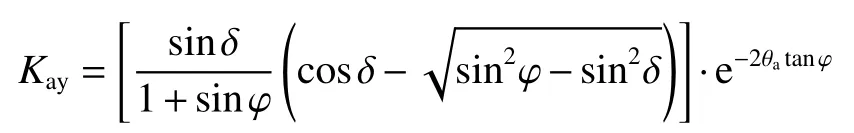
从而，作用在挡土墙上的主动土压力强度为：

拉应力区临界深度为：

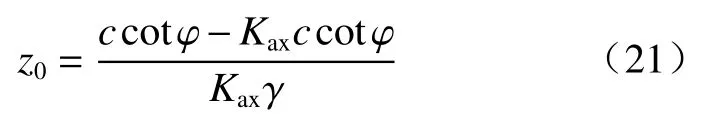
则：

将开裂土层深度范围内的土等效成均布荷载作用：

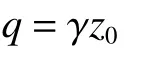
墙背切向力：

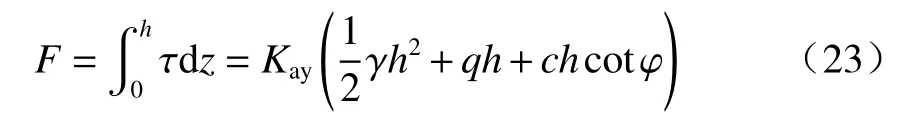
墙背水平力：

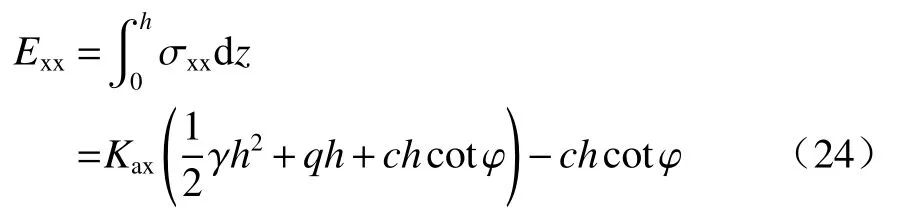
作用在墙背的主动土压力为：

主动土压力与墙背法线之间夹角：

同理可得墙背土体主应力偏转角θa为：

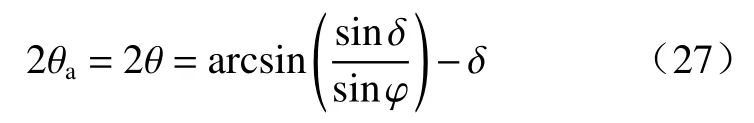
由图（5）可得墙土界面黏结力cw为：

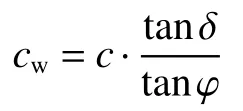
若墙背光滑（δ= 0），则有θa=0，cw=0，式（25）退化为：

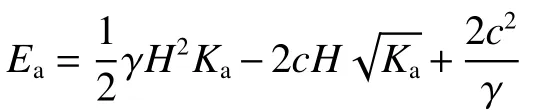
显然，若不考虑墙土摩擦角，主动土压力与朗肯主动土压力相同。

3 基于算例的对比分析

3.1 黏性填土挡土墙土压力计算的代表方法

（1）朗肯土压力理论。朗肯土压力理论是经典的黏性土土压力计算理论，是根据半空间的应力状态和土的极限平衡条件而得到的土压力计算方法。但朗肯理论假定挡土墙墙背光滑，忽略了挡土墙墙背与土体之间的摩擦和黏结力作用。

（2）卢廷浩法[8]。该法基于库伦理论平面滑裂面假定，考虑挡墙墙背与黏性填土的摩擦及黏结力、填土表面的裂缝及荷载以及滑裂面黏聚力的影响，由滑动楔体力矢图推导出主动土压力公式。以编程试算法得到滑裂面倾角的精确值求得主动土压力精确解。

（3）胡晓军法[11]。该法基于库伦理论平面滑裂面假定，考虑填土的黏聚力、墙土界面的摩擦力和黏结力，通过力矢多边形建立均布荷载作用下一般形式的黏性土挡土墙被动土压力计算公式。

（4）柯才桐法[17]。该法同样基于库伦理论平面滑裂面假定，但采用斜向条分法，考虑墙后黏性填土、墙土界面的摩擦力和黏结力以及均布荷载作用，通过土条静力分析，给出了一般形式的黏性土挡墙主动和被动土压力计算公式，并基于公式的特殊处理给出了滑裂角计算式。

3.2 对比分析

运用朗肯理论、卢廷浩法、胡晓军法、柯才桐法以及本文方法对以下2个算例进行计算并对比。

算例1：某挡墙墙高H=10 m，，墙背竖直，墙后填土水平，墙后填土表面无超载。填土参数为γ=18.6 kN/m3，φ=24°，其它有关参数及计算结果见表1，其中取cw=c·tanδ/tanφ。

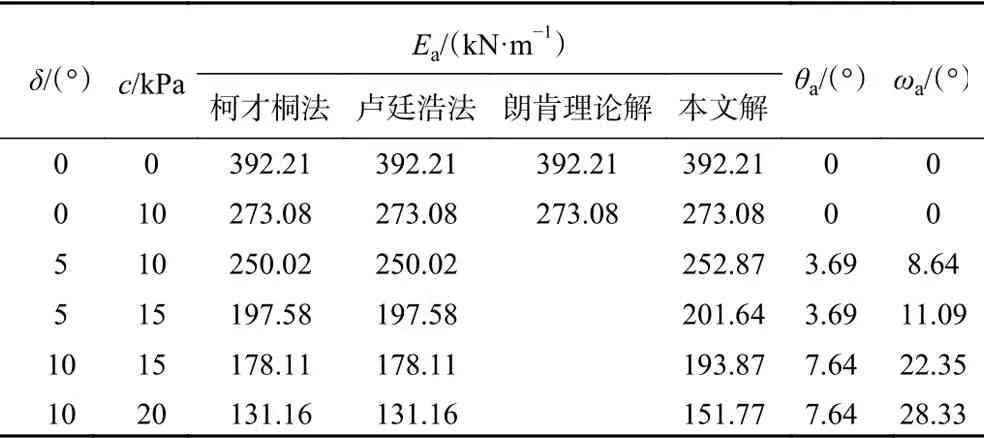
表1 主动土压力算例Table 1 Example for the active earth pressure

算例2：某挡土墙墙高H=8 m，填土参数为γ=18.6 kN/m3，φ=20°，墙背竖直，墙后填土水平，无超载作用，其它有关参数及计算结果列于表2，其中取cw=c·tanδ/tanφ。

由表1和表2可以看出，对于符合朗肯假设条件的情况，本文方法所得主被动土压力与朗肯理论的结果相同。对于考虑墙土摩擦和黏结力的黏性土挡墙主动土压力，本文方法所得结果大于其他学者的结果。对于考虑墙土摩擦和黏结力的黏性土挡墙被动土压力，本文方法所得结果小于其他学者的计算结果。本文方法主动和被动土压力计算结果与其他学者主动和被动土压力计算结果的差值变化规律一致，均随着δ、c的增大而增大。

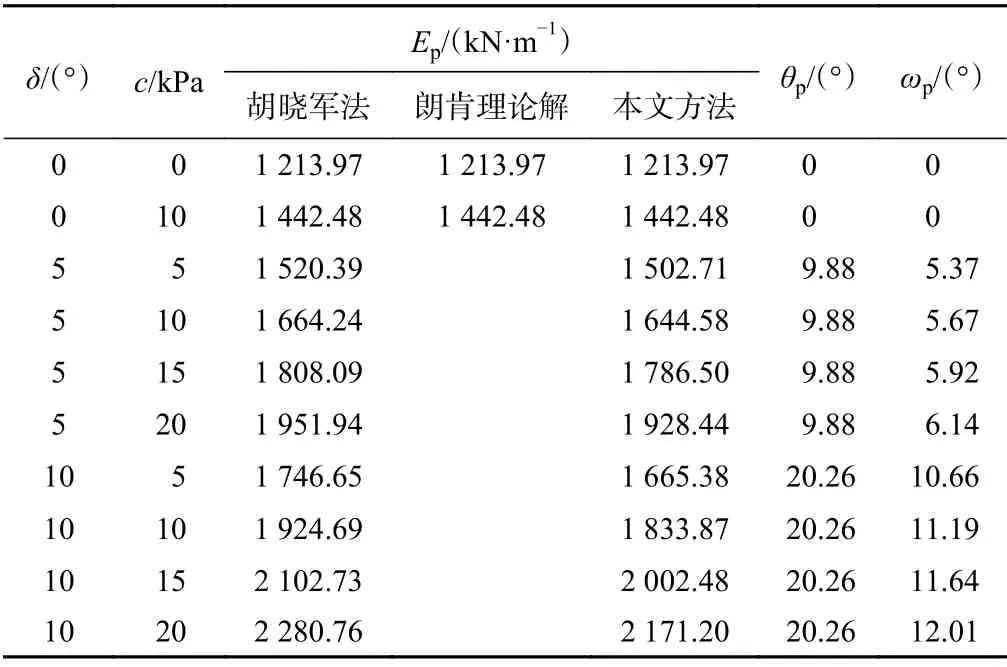
表2 被动土压力算例Table 2 Example for the passive earth pressure

表1和表2还表明，由于本文方法考虑了墙土界面黏结力作用，墙土界面的黏结力包含在土压力切向分量F中，使得土压力与墙背法线夹角ω大于摩擦角δ，且随着摩擦角δ、黏聚力c的增大而增大。墙土摩擦角越大，墙背土体主应力偏转越大，本文方法所得结果与他人结果相差也越大。然而当主应力旋转角θ=20°时sinθ≈θ仍成立，两者的误差只有0.007。显然，因考虑了墙后土体主应力偏转的事实，本文方法所得结果更客观、计算式更为简明易用。

4 参数敏感性分析

设挡墙高H=4 m，墙背竖直，墙后土体表面水平且无超载，填土γ=20 kN/m3，c=12 kPa。取φ=5°～35°，δ=（0～0.7）φ，分析δ、φ对土压力的影响（图6、图7）。图6和图7分别反映作用在挡墙墙背的主被动土压力随δ和φ的变化情况。对于主动土压力，当φ<10°时，主动土压力随δ、δ/φ增大不断减小，且减小的速度在逐渐减缓；当φ≥10°时，主动土压力随δ、δ/φ增大先减小后增大，但总体变化不大；当δ不变时，主动土压力随φ增大不断减小，且减小的速度在逐渐减缓。被动土压力则随δ、φ、δ/φ的增大不断增大，且增大的速度在逐渐加快。主动土压力随δ值增大不断减小，但总体变化不大。φ值对主被动土压力影响均较δ显著。

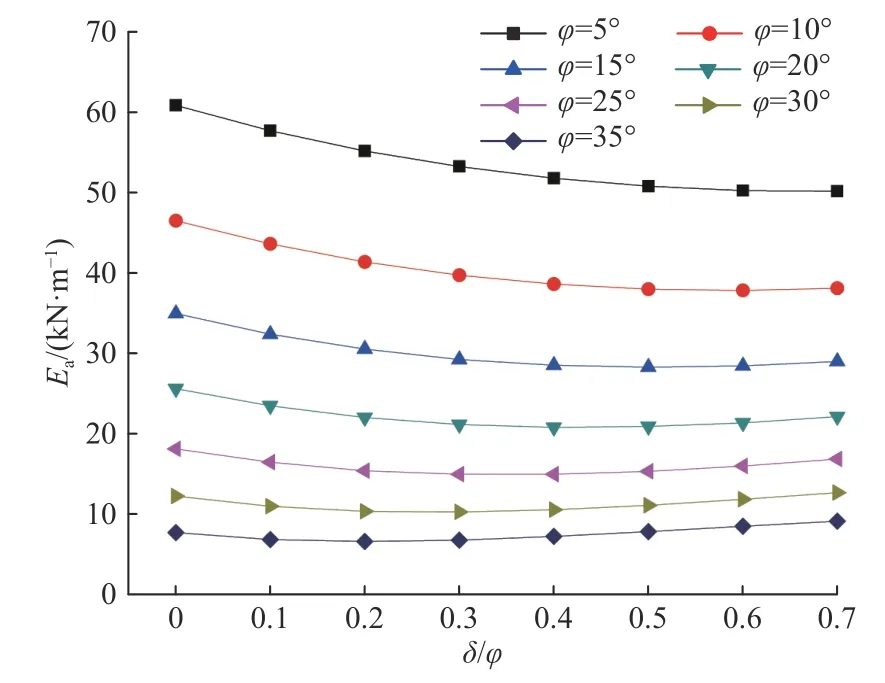
图6 主动土压力随δ/φ的变化Fig.6 Change of the active earth pressure with δ/φ

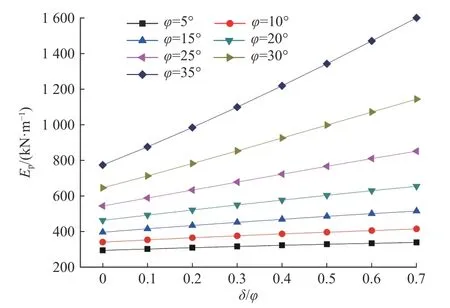
图7 被动土压力随δ/φ的变化Fig.7 Change of the passive earth pressure with δ/φ

5 结论

（1）采用主应力旋转处理墙后土体主应力偏转现象，推导出考虑墙土摩擦和黏结力作用的黏性土挡墙土压力计算式，朗肯土压力公式只是新方法公式的特例。由于墙土界面黏结力作用，土压力与墙背法线的夹角ω大于摩擦角δ。

（2）当黏性土内摩擦角φ较小时，墙土界面黏结力影响较小，随着墙土摩擦角δ的增大，主动土压力不断减小，且减小的速度逐渐减缓；当φ值较大时，随着墙土摩擦角δ的增大，墙土界面黏结力加强，主动土压力先减小后增大。被动土压力随着墙土摩擦角δ的增大不断增大，且增大的速度在逐渐加快。随φ值增大，主动土压力减小且减小的速率在逐渐减缓，被动土压力增大且增大的速率在逐渐加大。φ值的影响比δ值更明显。

（3）对于主动土压力，本文方法所得结果大于其他学者的结果。对于被动土压力，本文方法所得结果小于其他学者的计算结果。本文方法主被动土压力计算结果与其他学者主被动土压力计算结果的差值变化规律一致，均随着δ、c的增大而增大。本文方法考虑了墙后土体主应力偏转的事实，计算结果更客观。