基于TPA和遗传算法的动力总成悬置系统优化设计
2021-07-22潘公宇付博文王功强陈清爽
潘公宇, 付博文, 王功强,, 陈清爽, 朱 瑞, 李 东,
(1. 江苏大学 汽车与交通工程学院,江苏 镇江 212013;2.江西省汽车噪声与振动重点实验室(江铃汽车股份有限公司),南昌 330013)
汽车工业的不断发展促进了车辆各项性能的进步,对乘坐舒适性等车辆的品质特性的关注度越来越高,因而车辆的NVH特性研究也变得越来越重要。车辆的NVH问题是一种系统性的问题,较大的激励源、振动路径耦合等均可能是车辆振动异常的问题来源[1]。以怠速工况为例,整车的振动源主要来自发动机,而作为隔离发动机与车身振动的部件,悬置系统对整车NVH特性的影响就显得尤为重要[2]。
目前针对悬置系统的研究大多基于悬置系统本身,从6自由度的模型出发,合理配置悬置系统固有频率,优化解耦率、支反力、隔振率等,忽略了悬置系统在整车模型中所起到的作用[3]。而从整车角度考虑的话,不可避免地要建立多自由度模型进行仿真分析,Jin等[4]建立了包括悬置系统在内的13自由度整车模型,可模拟分析不同悬置刚度参数下,整车的振动响应。Shi等[5]将副车架和动力总成的自由度加入到16自由度模型,分析悬置系统的隔振性能与整车振动的相关性。Mohammad等[6-8]研究团队为研究动力总成的各阶固有频率与副车架,车身等部件之间的关系,以及与刚度,位置,惯性参数等性能参数之间的影响,建立了五种整车模型,并分别分析了各个模型的适用范围及识别精度。从该角度来分析悬置系统特性所需考虑的因素较多,模型复杂,分析效率低下,且各仿真输入值均为模拟量,与实际情况差别较大。
本文针对某前置前驱、发动机横置的乘用车在怠速工况下,主驾驶座椅导轨和方向盘处振动幅值较大,主观感受较差的问题,利用悬置刚度法传递路径分析方法,建立传递路径分析模型,将悬置系统的刚度值与车内各目标点的振动幅值相联系,以目标点振动幅值满足要求为首要条件,同时合理配置悬置系统的固有频率和解耦率,对悬置系统展开优化研究。
1 怠速抖动分析
动力总成主要由发动机、变速器、离合器等组件组成。在怠速工况下,变速器、离合器等组件处于不工作状态,因此发动机为主要激励源。发动机运行过程中,活塞的往复运动、旋转运动以及气体的燃烧会产生不平衡力与不平衡力矩[9-10]。悬置系统作为动力总成与车身的连接机构,不平衡力与不平衡力矩经悬置系统传递至车身,并通过振动影响到车内乘员。本文研究车型搭载三缸发动机,怠速转速为850 r/min,其1阶频率为14.17 Hz,点火频率为21.25 Hz。图1为部分车内目标点怠速开/关空调工况的频谱图,座椅导轨处的振动以1阶和1.5阶能量为主,0.5阶、3阶和4阶能量其次,其中X向的振动主要体现在基频14.17 Hz附近。
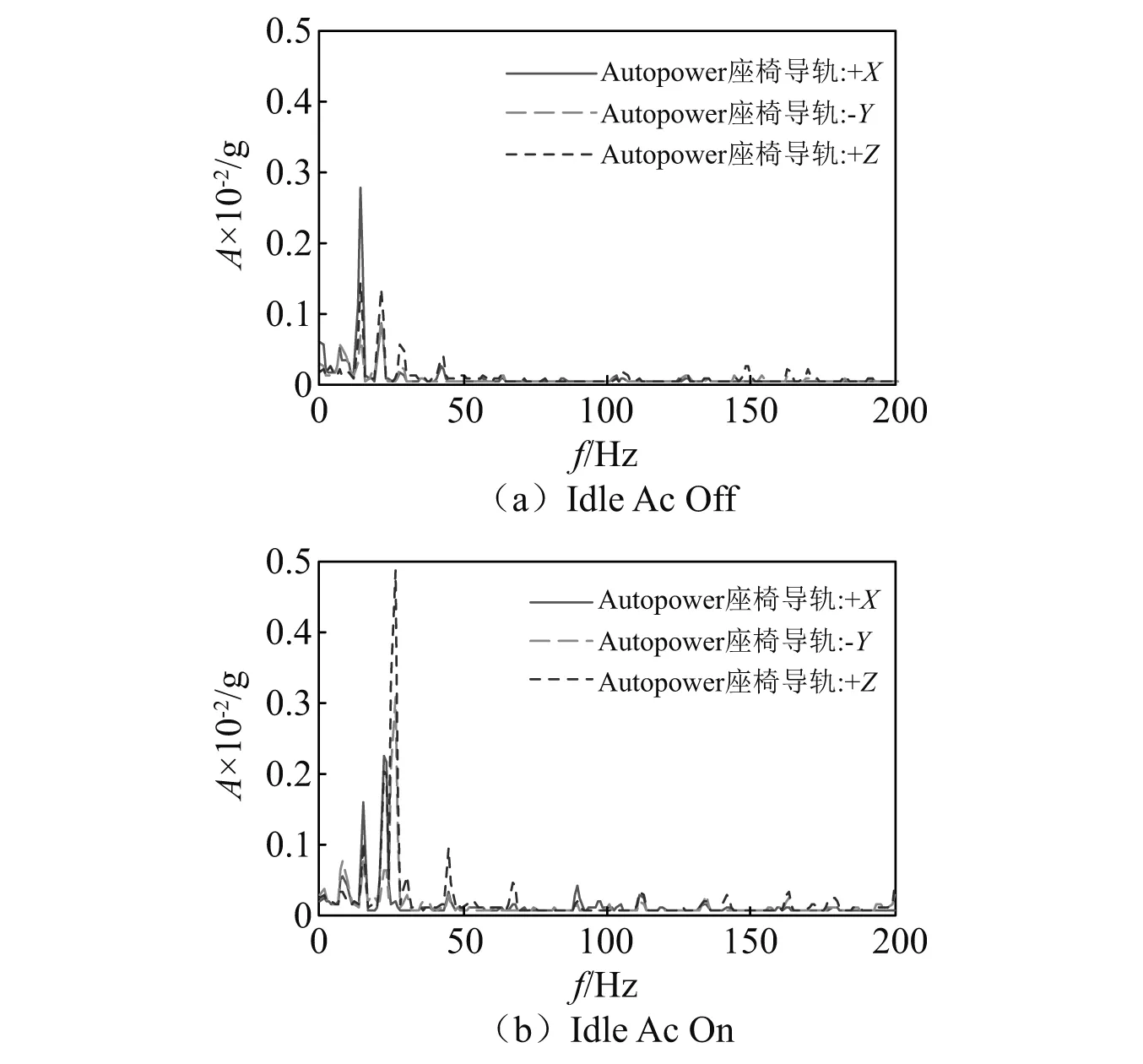
图1 方向盘振动加速度频谱
悬置系统通过车身侧支架、动力总成侧支架连接动力总成与车身。支架-悬置-支架组成了隔振系统,且支架均具有刚度,可简化为具有刚度的弹簧,支架、悬置、支架可简化3个串联的弹簧模型,动力总成侧支架、悬置、车身侧支架的刚度分别用KPT,KM,KB表示,如图2所示。动力总成悬置系统的总刚度如式(1)所示。支架刚度远大于悬置刚度,因此悬置系统的刚度即为悬置的刚度。动力总成的隔振效果主要取决于系统的惯性特征、悬置的刚度和阻尼、安装位置和方向,以及动力总成的不平衡力和力矩等。对于量产车型,动力总成及悬置安装位置以确定,故往往通过调整悬置刚度对隔振效果进行调整。
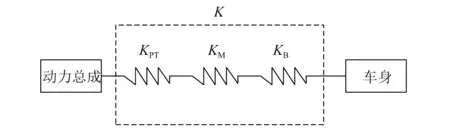
图2 弹簧串联模型
(1)
2 传递路径分析方法
2.1 传递路径分析方法理论
车辆的NVH问题多体现在乘员与车辆接触较多的部位,如方向盘、座椅等,而问题的来源主要包括2个部分,发动机等激励部件和车身子结构等传递部件。振动能量由激励部件产生,经子部件传递,最终到达系统的响应点,产生异常的NVH问题。响应点处的振动量是由各路径贡献量叠加得到,每一条路径都有独立的激励源和传递特性,而传递路径分析方法,即传递路径分析(transfer path analysis,TPA)便是用来详细研究各激励源与路径特性对响应点的振动贡献(见图3)。
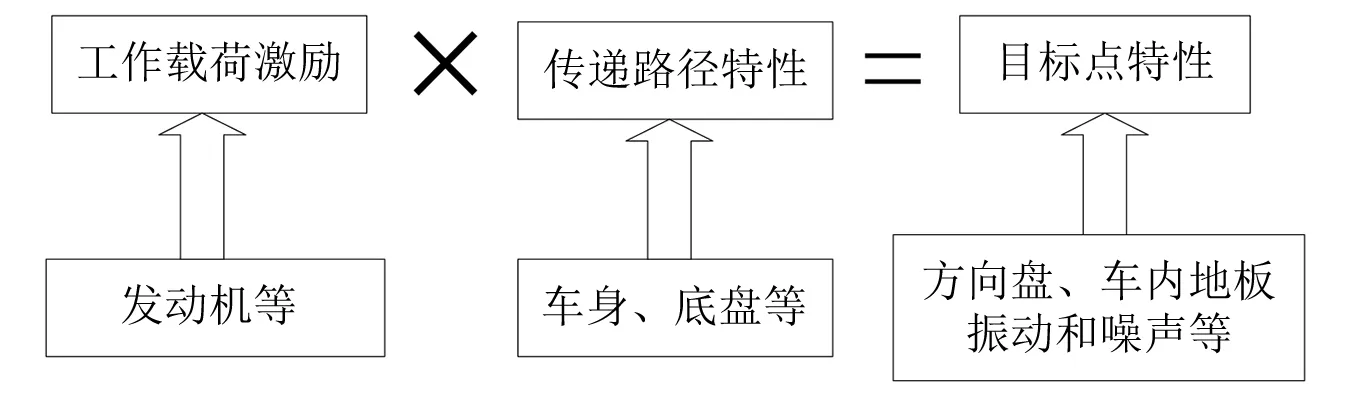
图3 TPA模型
TPA方法的理论公式如式(2)所示
(2)
式中:Y(ω)为目标点处的总贡献量;Hi(ω)为频率响应函数;Fi(ω)为结构载荷;n为结构传递路径的数量;ω为频率。由式(1)可以看出,TPA方法不仅可以分析各路径对目标点的贡献量,在已知激励载荷和频响函数时,还能对目标点进行振动响应预测。与此同时,在利用TPA技术进行振动响应分析时,所需的数据也包括这两种。
2.2 载荷识别与车内评价点预测
在对软悬置的激励载荷进行识别时,悬置刚度法的识别精度是最高的[11],其计算公式如式(3)所示
(3)
式中:Fi(ω)为载荷大小;Ki(ω)为悬置等弹性元件的动刚度值;aai(ω)和api(ω)分别为悬置等弹性元件的主、被动端处的振动加速度值。
显然,在已知悬置元件的动刚度和主被动端的振动加速度时,悬置处的激励载荷便能通过式(3)计算得到。频响函数是由系统的固有特性决定的,可通过锤击法测试得到。因此,车内评价点的振动量可由式(4)计算得到。
(4)
本文关注的车内评价点为座椅导轨和方向盘,对于三点悬置系统形成3×3=9输入、2×3=6输出的传递路径模型,如图4所示。在同时获取系统的频响函数以及悬置主、被动端的振动加速度时,车内评价点的振动响应量便可由悬置元件动刚度表示(设计阶段,因悬置元件刚度值未知,无法获取准确的悬置端振动加速度值,主动端、被动端振动数据可通过标杆车的振动数据及隔振率等要求确定)[12]。
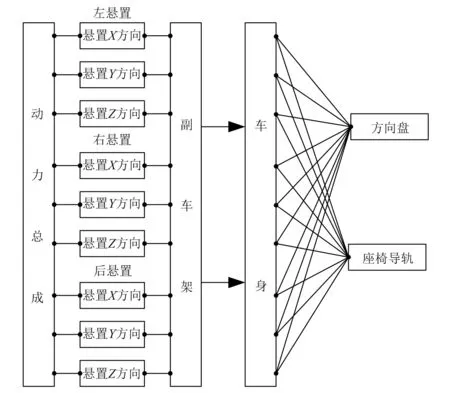
图4 传递路径分析模型
3 悬置系统优化模型及评价标准
3.1 动力总成悬置系统6自由度模型
机械系统的振动特性由其本身的惯性,刚度,阻尼等决定,因此在从整车角度进行悬置系统优化分析时,系统本身的固有频率,解耦率等基本特性也是必须要考虑的[13-14]。由于动力总成的固有频率远大于悬置系统的固有频率,因此可将动力总成视为刚体,悬置系统为具有6自由度的三向刚度弹簧,三点悬置系统的动力学模型如图5所示。

图5 动力总成悬置系统6自由度模型
在动力总成质心坐标系中G-XYZ中,X轴平行于发动机曲轴,指向发动机前端,Z轴平行于活塞方向,指向正上方,Y轴由右手法则确定。取坐标轴三向平动x,y,z和三向转动,θx,θy,θz来描述动力总成运动广义坐标,如式(5)所示。
q={xyzθxθyθz}T
(5)
3.2 悬置系统固有特性计算
根据系统动力学可知,悬置系统振动微分方程如式(6)所示
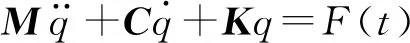
(6)
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F(t)为系统所受到的激振力。考虑到悬置系统的阻尼对其固有特性的影响较小,因此一般将其简化为无阻尼自由振动系统,如式(7)所示。计算该微分方程即可得到悬置系统的固有频率及其振型。
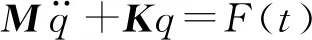
(7)
3.3 悬置系统模态解耦率计算
在多自由度振动系统中,各自由度之间的振动相互耦合现象是普遍存在的,这也是减振的巨大障碍,因此精确计算各阶模态解耦率对于悬置系统的优化设计而言具有重要作用。目前应用较为广泛的方法便是能量解耦法,该方法从能量的角度出发,使各自由度上激励力所做的功全部转化为系统沿该方向上的能量,其模态解耦率可由式(8)计算所得。
(8)
式中:Tp为模态解耦率;Ai为系统第i阶主振型;(Ai)k为第k个元素和第i个元素;mkl为系统质量矩阵第k行l列元素。
3.4 设计变量
针对悬置系统的优化变量一般包括悬置元件的刚度、阻尼、支撑位置、角度等,而针对发动机前舱已完成设计制造的目标车型来说,改变悬置元件的支撑位置和角度会显著增大制造成本,极易与其他结构部件发生运动干涉,悬置元件的阻尼系数对其固有频率的影响较小,在频率配置和解耦率分布等方面作用不大,而改变悬置元件的刚度值则较为简便,因此,本文选取3个悬置元件的各向静刚度值作为优化变量,共计9个变量,即
X=(kui,kvi,kwi), (i=1,2,3)
(9)
3.5 约束条件
约束条件一共包括两类:刚度的取值范围和系统各向固有频率,解耦率要求。悬置刚度的取值范围需满足悬置本身所起的作用,及“支撑”、“限位”和“隔振”。通过分析动力总成的质量以及悬置的安装位置和角度,可初步计算出悬置要满足“支撑”作用所需的刚度限值。在此基础上,过大的刚度值会使悬置的刚性过大,“隔振”效果欠佳,而过小的刚度值则会在动力总成运作时,与发动机舱内其他结构部件产生运动干涉,造成零件损坏。本文所研究的乘用车动力总成采取三点悬置,即左悬置、右悬置和后悬置,如图6所示。

图6 悬置结构示意图
动力总成的质量主要由左悬置、右悬置支撑,其中后悬置为防扭拉杆,其v,w向刚度值较小。初步设定3个悬置的三向刚度值范围,如表1所示。

表1 悬置静刚度取值范围
悬置系统各向固有频率和解耦率的要求一般由车型和动力总成本身特性所决定,对于本文所研究的目标车型,可做如下要求:
(1)悬置系统各频率间隔需大于1 Hz;
(2)1阶激励频率避开各个刚体模态频率,Roll模态频率与1阶激励频率之间至少避开1 Hz,控制它与1.5阶激励频率之比;
(3)Roll模态与Yaw模态需避开1阶频率;
(4)固有频率尽量避开人体对座椅z向比较敏感的4~7 Hz,同时避开悬架传递过来的Hop & Tramp频率;
(5)最大固有频率应满足隔振要求,要小于有效隔振频率15.38 Hz,建议Pitch和Bounce小于1.5阶激励频率的1/2;
(6)考虑整车操稳性,悬置系统频率需要大于5 Hz。
考虑到z向、Roll、Yaw、Pitch向均受不平衡激励,故z向、Roll、Yaw、Pitch的解耦率应大于等于90%,其他方向应大于等于85%。综上所述,对悬置系统的各阶模态频率和解耦率要求见表2。
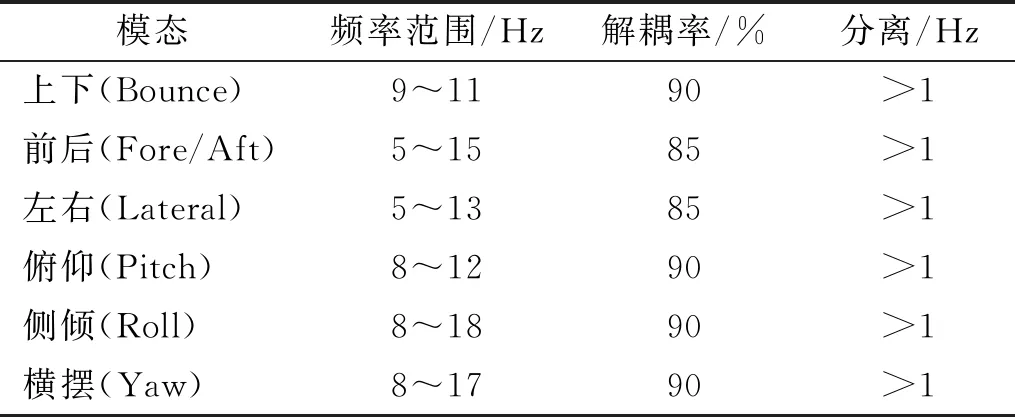
表2 悬置系统模态频率和解耦率要求
3.6 目标函数
悬置系统固有频率和解耦率的合理匹配可大大降低共振的风险,因此考虑将固有频率和解耦率的合理配置作为优化目标,其目标函数分别如式(10)和式(11)所示
(10)
(11)
式中:S为固有频率与期望值的差值;E为6个广义坐标对应的能量分布加权和;βi和αi分别为第i阶(i=1~6)固有频率和解耦率的权系数,考虑到z向、Roll向为主要不平衡激励方向,故z向、Roll向αi取0.2,其余方向选为0.15,βi均取1/6;fil和fiu分别为第i阶期望固有频率的上下限,fi为第i阶计算得到的固有频率;DIPik为第i阶固有频率的振动能量占优方向所占总能量的百分比;M(k,j)为质量矩阵中第k行,第j列的元素;φ(k,i)和φ(j,i)分别为在第i阶振型下,第k个和第j个元素。
基于前述所研究的传递路径分析方法可知,通过测取悬置连接点处至车内各目标点的频响函数,计算各悬置处的激励载荷,便可将悬置处的动态特性和车内各点的振动响应相联系,建立以控制车内振动为目的的悬置优化目标函数,式(12)表示为在怠速工况下,座椅导轨处的振动优化目标函数。
(12)
式中:α1和α2为各点的权系数,α1和α2均取0.5;S1(ω)和S2(ω)分别为座椅和方向盘的振动量与期望值之间的差值;a(ω)和au(ω)分别为计算值和期望值,均为怠速工况下各点振动的RMS值(有效值)。该目标函数在怠速工况下分为Idle Ac On和Idle Ac Off两种状态,函数形式一致,期望值不同。
综上所述,悬置的多目标优化函数如式(13)所示。
(13)
3.7 优化方法
基于车内NVH特性进行悬置系统优化时需考虑较多因素,目标函数较多,属于典型的多目标优化问题[15]。针对多目标优化问题,一般分为两类:归一化和非归一化。将所有的目标函数通过加权的方法整合为单目标函数即为归一化方法,该方法的核心特点是需要确定适合于各目标函数的权重系数,主观性较大,且在求解最优解时,若Pareto解集前沿形状存在凹陷部分时,该方法无法求得最优解。基于此,本文所建立的悬置优化目标函数采用非归一化的方法,即直接处理多目标函数,求解最优解。基于遗传思想的非支配排序算法NSGA-II是目前较为成熟,高效的多目标优化算法。根据上述所建立的各目标函数及设计变量,利用MATLAB软件可建立基于NSGA-II算法的优化模型,其主要流程如图7所示。其中,算法内各优化参数设置如表3所示。

表3 优化参数设置
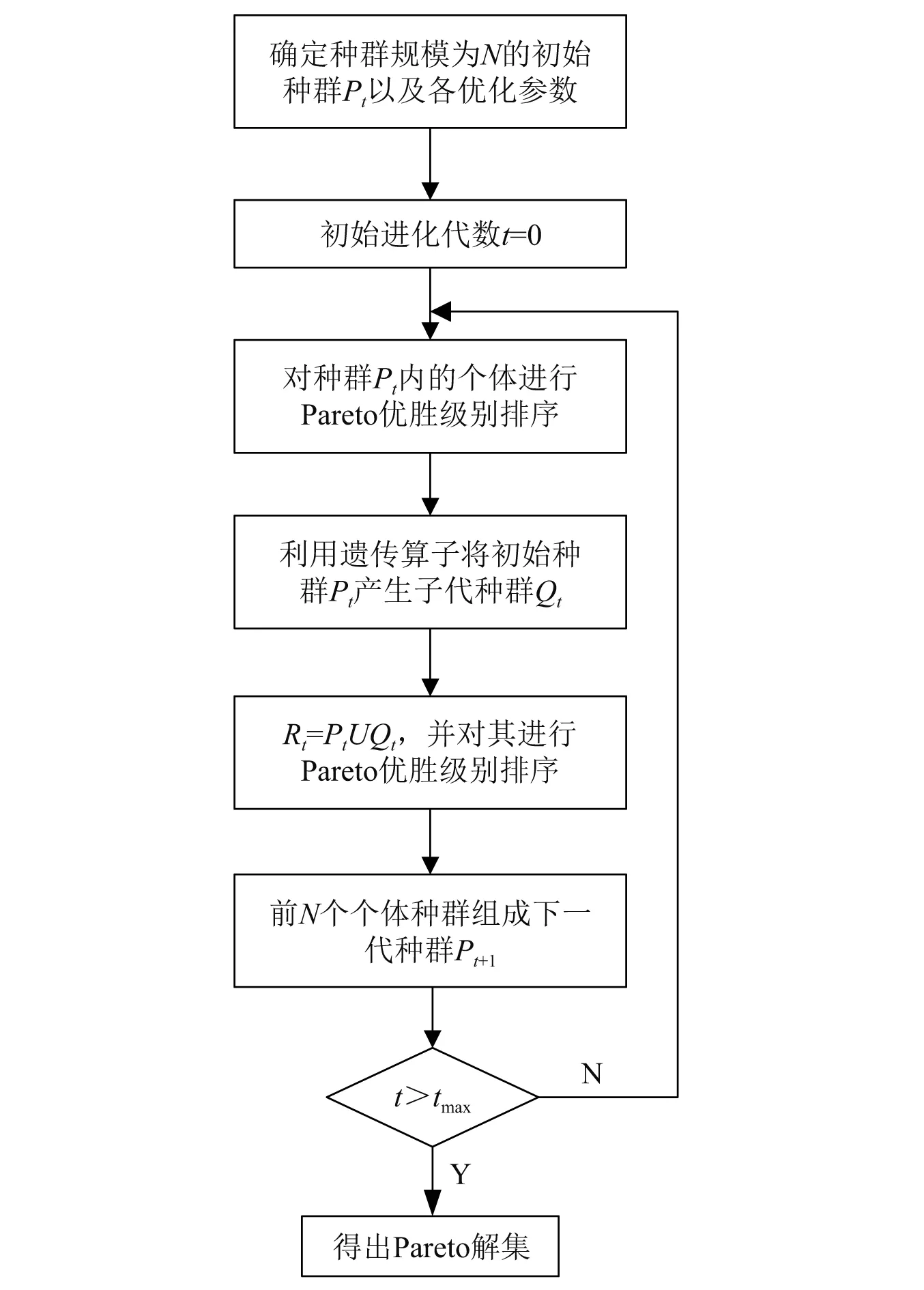
图7 NSGA-II算法流程图
3.8 评价标准-隔振率
悬置系统最重要的功能便是隔振,主要表示为悬置主动端与被动端振动响应量的比值,其计算公式如式(14)所示。工业界一般认为,悬置元件的隔振率达到20 dB便可满足大部分的NVH要求。该要求过于笼统,并不适用于精确地评价悬置元件的隔振性能。因此,本文在此要求的基础上,加入和标杆车隔振率的对比,来进一步说明本次研究所得的悬置元件的隔振性能。
(14)
4 TPA实验及悬置优化
4.1 TPA模型建立及数据测取
本次研究对象为一款搭载1.0 t三缸汽油发动机的乘用汽车,动力总成悬置共有3个,其中右侧发动机悬置为液压悬置,其余为橡胶悬置。悬置各主,被动端分别安装1个三向振动加速度传感器,用来测取振动输入信号,在方向盘和驾驶员座椅导轨2个位置分别安装1个加速度振动传感器测取响应信号,这样就形成了3×3=9输入、2×3=6输出的传递路径模型。其中测试工况为Idle Ac On和Idle Ac Off工况两种。部分传感器布点位置如图8和图9所示。

图8 悬置处传感器布点位置

图9 目标点处传感器布点位置
在对整车进行频响函数测量时,为了避免各路径的相互耦合,提高测量结果的准确性,需将动力总成,悬置等部件拆除,用尼龙绳将整个车身吊起。保留TPA试验时,悬置被动端以及各响应点,参考点处的传感器,利用力锤在悬置传感器附近施加激励,测取各传感器信号以及相应的传递路径频响函数信号。图10为本次实验所采用的激励力锤。图11为部分频响函数测量结果。

图10 实验用力锤
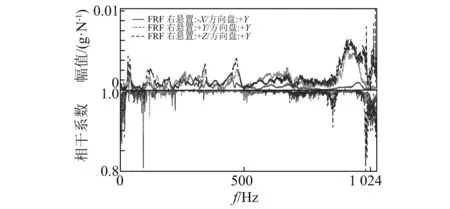
图11 右悬置-方向盘Y向频响函数
4.2 悬置系统优化计算
依据上述建立的悬置优化模型,利用NSGA-II算法可获取最优静刚度值的Pareto解集,根据橡胶悬置的可制造性及刚度的合理性可选择一组较为合适的静刚度值,如表4所示,固有频率分布和解耦率可见表5。

表4 优化后悬置各向静刚度值

表5 优化后悬置系统的固有频率和解耦率
显然,优化后悬置系统各阶频率之间均大于1 Hz,解耦率均大于90%,这可极大降低各方向之间发生共振的风险,优化后的结果基本满足要求,即:
(1)Bounce方向频率为8.4 Hz,避开了人体较为敏感的4~7 Hz;
(2)Pitch方向频率小于发动机怠速激励频率(21.25 Hz)的一半,即9<10.625;
(3)Roll方向频率为15.3 Hz,与发动机1阶激励频率(14.33 Hz)相差1 Hz,发动机1.5阶激励频率(21.25 Hz)与Roll方向频率之比为1.392,大于1.2;
(4)优化后悬置系统的最小频率为6 Hz,大于5 Hz,满足整车的操稳性要求。
将优化后的悬置刚度值代入上述建立的传递路径分析模型,即可预测出采用优化后的悬置系统,车内各目标点模拟振动响应。其中,在计算悬置处的载荷值时,考虑利用参考车型悬置处的振动数据作为输入量,因为参考车型的数据一般作为目标车型的上限值,故在采用该输入量时,预测响应比实际值偏大,可作为悬置元件试制之前的参考验证。
5 整车匹配实验验证
由于理论分析模型的简化,系统的非线性,以及生产制造中的误差等,都会导致计算结果与实际装车实验结果存在偏差,因此简单依靠仿真分析和优化是远远不够的。为进一步验证上述悬置设计方案的有效性,现根据优化结果试制悬置,展开整车匹配测试验证。
5.1 实验设备及方案
本次实验主要考虑Idle Ac On和Idle Ac Off两种工况,其中:Idle Ac On表示整车怠速时,将前车灯和后车窗的防冻装置打开,空调制冷调至最大,送风机调至最小风速,发动机冷却风扇保持最大转速;Idle Ac Off表示整车怠速时,所有附属装置都关闭,发动机冷却风扇关闭。实验设备主要包括笔记本电脑,PCB加速度传感器,LMS数采系统等。
为综合验证优化后的悬置系统的优越性,本次实验主要测取悬置元件的隔振率和车内各目标点的振动响应量,以此来分别评价悬置系统本身的隔振量以及对整车NVH性能的影响。
5.2 隔振率测试结果
图12和图13分别表示Idle Ac Off和Idle Ac On两种工况下,3个悬置的隔振率。由下述对比图可以看出,新试制的悬置元件在怠速工况下,隔振量均大于20 dB,且目标车型绝大部分方向的隔振量表现优于标杆车,在Idle Ac Off工况下,右悬置Z向,后悬置的X向、Y向,以及Idle Ac On工况下,后悬置Y向、Z向的隔振量虽小于标杆车,但其均处于30 dB附近,差异可忽略不计。
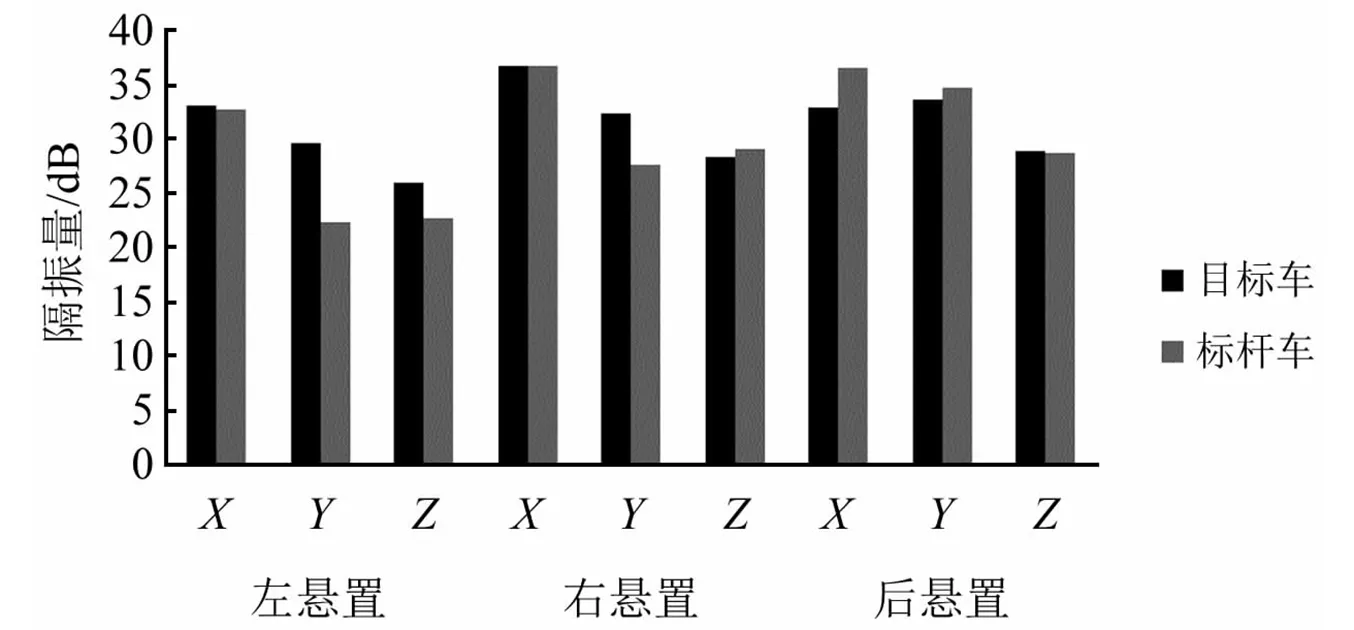
图12 Idle Ac Off工况下各悬置隔振量对比

图13 Idle Ac On工况下各悬置隔振量对比
5.3 车内各目标点测试结果
悬置系统的最终目的是隔离动力总成的振动传递到车内,因此从整车角度来评价悬置系统的隔振性能是最直接的手段。图14和图15分别表示Idle Ac Off和Idle Ac On两种工况下,车内2个目标点处的振动响应量的对比。由对比图可以看出,在Idle Ac Off工况下,目标点振动响应幅值基本与标杆车相持平,主驾座椅导轨的X向振动水平不如标杆车,分别为0.003g和0.002g,但低于目标设定值0.01g,因此此处可判定为满足设计要求。在Idle Ac On工况下,方向盘X向,Y向振动表现不如标杆车,分别为0.021g和0.032g,但均低于目标设定值0.035g,其余位置基本与目标车持平。这说明本文所提出的悬置系统优化模型准确有效,优化后的悬置系统性能优异。
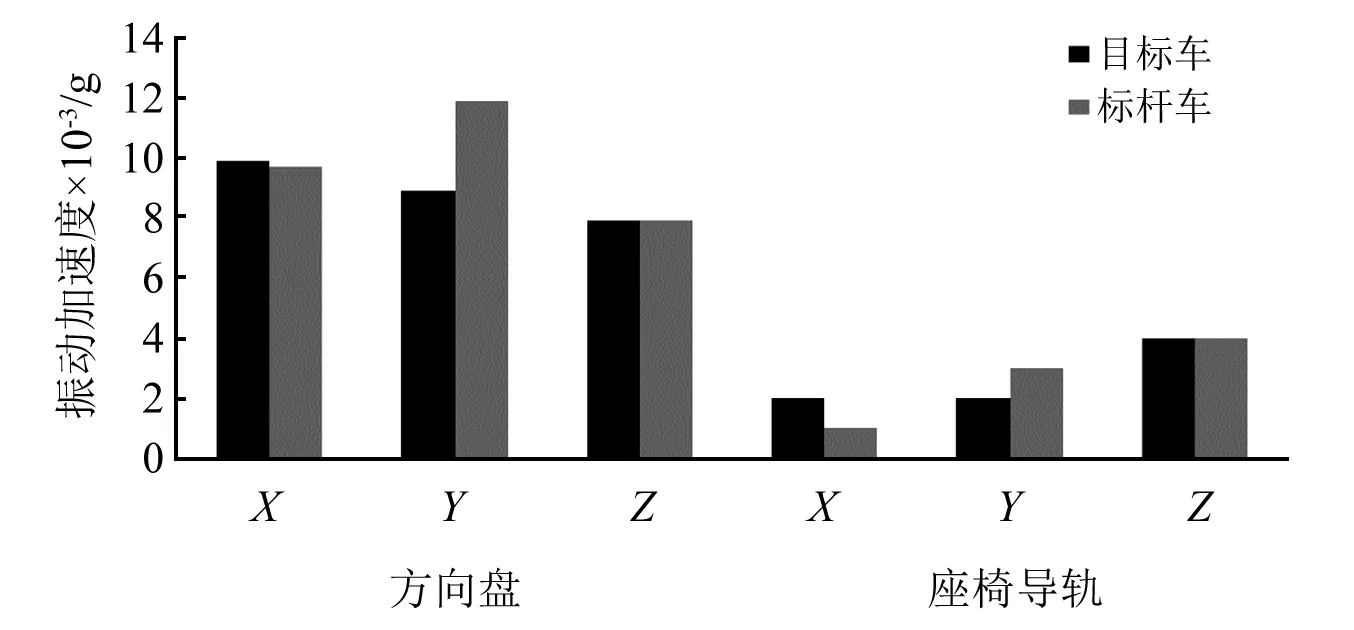
图14 Idle Ac Off工况下各点振动幅值对比
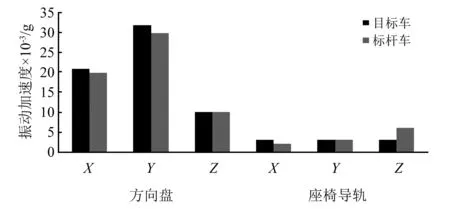
图15 Idle Ac On工况下各点振动幅值对比
6 结 论
由于单纯的考虑6自由度模型对悬置系统进行优化具有一定的局限性,其优化结果并不能满足整车的NVH水平。本文利用TPA方法,将悬置系统与整车系统相联系,建立了更全面的悬置系统优化模型,取得了如下成果:
(1)综合利用TPA理论和悬置系统6自由度模型,建立了以满足车内振动要求,并同时合理分配悬置系统的解耦率和固有频率的悬置系统优化模型。
(2)根据建立的悬置系统优化模型,利用TPA测试来获取相应的输入数据,并利用遗传算法NSGA-II来对该模型进行优化计算,从而获得最终的优化结果。
(3)对优化后的悬置系统进行零件试制,并装车进行匹配测试,从隔振率和车内振动响应2个角度来验证优化结果的准确性,结果表明,优化后的悬置系统能有效改善隔振性能,目标车的NVH性能优于标杆车,验证了所提出模型及优化方法的有效性。
