负压波与小波分析定位供热管道泄漏
2021-07-22石光辉齐卫雪李建刚
石光辉, 齐卫雪, 陈 鹏, 樊 敏, 李建刚
(太原市热力集团有限责任公司,太原 030000)
集中供热管网作为一个城市的基础设施,安全高效运营尤为重要。但是每年都会因为热力管道泄漏出现大量的经济及资源损失[1-2],老旧管网检测手段不到位,部分管网甚至完全没有检测手段。有很多原因会造成管网的泄漏,如管道内外腐蚀、焊缝破裂、局部水流冲击、管线超压、施工质量低下、运营人员误操作等[3-4]。如果管网发生泄漏而没有及时发现并处理会引发巨大的问题。持续的管网泄漏会造成能量浪费、大幅度增加运营成本。此外,爆管事故也是重大的安全问题。然而,当泄漏事故发生时,泄漏点往往很难迅速定位,极大影响系统的安全运行。随着供热成本与供热质量的不断提升,供热管道泄漏检测与控制变得越来越重要。
以太古供热系统一级供热管网为例,管网全长900 km左右,由于管网多,管网建设年代老旧不一,自系统投运以来,每年都会碰到不同程度的失压突发故障工况,小到热力站管道,大到DN1400主管线,漏点查找时间由10 min到4 h不等,隔离时间由几分钟到2 h不等,在较长时间的漏点查找及隔离下,可能会导致系统停运而对供热产生较大影响。
管道泄漏涵盖范围广,有学者通过泄漏声振动检测定位法漏点[5],也有学者通过压缩感知和深度学习理论为泄漏提供全新的信息挖掘[6]。在输油管道泄漏研究中,存在一种基于负压力波[7-8]检测的方法。该方法采用声波原理法[9],简单实用,不需要增加大量监测点,并且有较快的检测速度。但是与输油管道不同,供热管网存在大量分支,导致负压波在传播过程中产生不同程度的衰减难以捕捉,并产生大量的二次水击波,使得波动变得复杂多变,加大了压力波分析的难度。同时负压波法难以准确区分泄漏造成的压力波信号和其他操作,特别是管线运行过程中,主要干扰来自两端泵站操作,如水泵启停、阀门调节、其他管网震动等造成的负压波信号,所以当实际使用时会产生大量的误报[10]。因此传统的负压波法难以用于管网的泄漏检测[11-12]。2002年,学者针对输油管道提出以小波变化为基础的泄漏点定位算法,小波分析法的误报警率要低于负压波,负压波的泄露检测灵敏度高于小波分析[13-15],因此本文拟通过实验的方法验证小波分析与负压波相结合的方法对管道泄漏点进行定位的可行性与精确度。
1 系统原理
1.1 利用水击波传播原理推测泄漏位置
当管道发生严重泄漏事故时,泄漏点的压力迅速大幅下降,从而形成负压水击波,负压波沿着管道向两侧传播。水击波的传播速度取决于管道,即可事先知道管道内实际波速的大小。因此,在管道上设置多个压力变送器,当检测到压力波动较大的水击波,则利用专业算法分析接收到的水击波压力波动,将分析得到的水击波产生时间记录下来,根据多个压力变送器测到水击波的时间点,分析时间差,反推出水击波的源头。泄漏点检测原理简图,见图1。
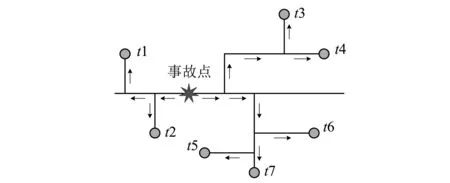
图1 泄漏点检测原理简图
其中,水击波波速a可用式(1)计算
(1)
式中:D为管径;E为管材弹性模量;e为管道壁厚;K为流体体积弹性模量;ρ为流体密度。
对于油气长输管道这类基本没有分支的管道,此方法具有良好的效果。但热网与之相比存在大量分支和环路,分支会使得水击波产生明显的衰减,某些测点位置可能无法得到明显的信号。因此热网无法简单照搬该方法,需要考虑热网自身的特性。
1.2 分支对水击波的影响
分支管道示意图如图2所示。其中,管道1、管道2、管道3的管径分别为D1,D2,D3,波速分别为a1,a2,a3。正常运行时的水压线如图3中虚线所示。下面分别讨论泄漏点位于干管和支管两种情况。

图2 分支管道示意图
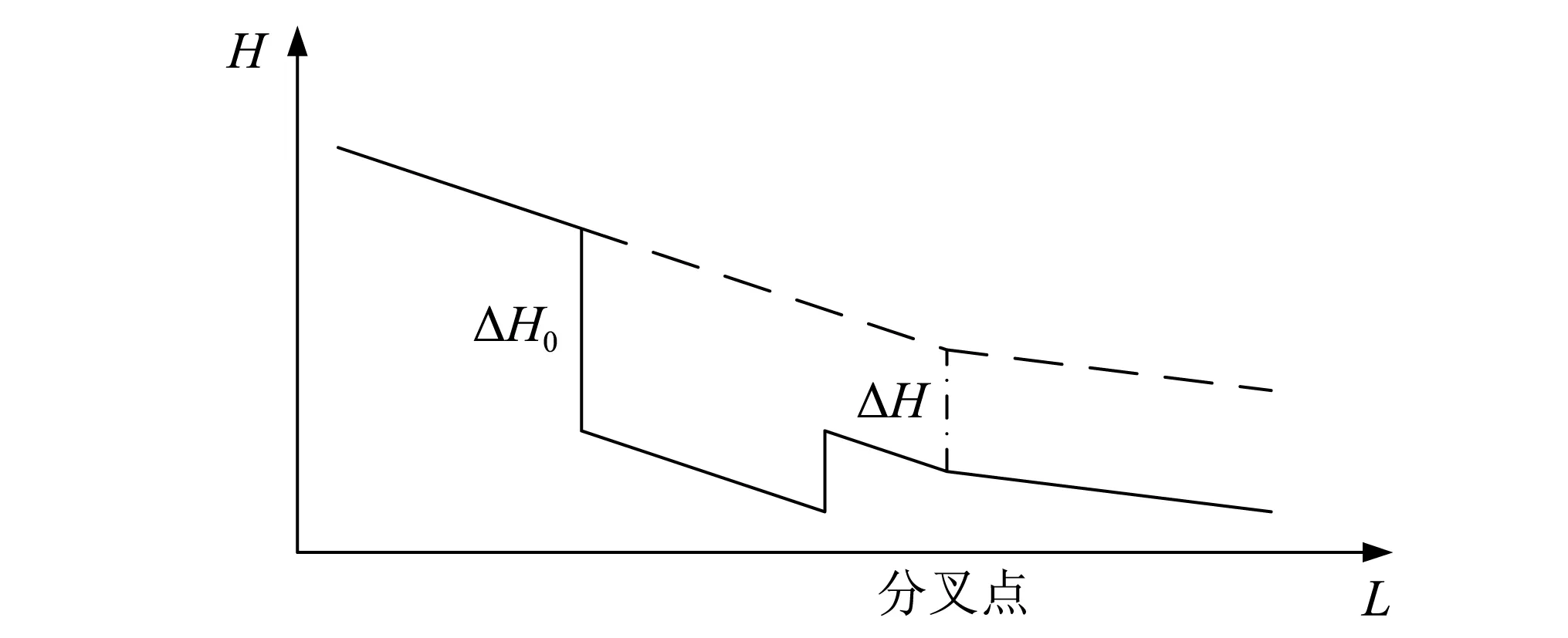
图3 水击分支处的水击波
(1)泄漏点位于干管
若泄漏点位于干管,即管道1某处出现一个大小为ΔH0的负压水击波时,考虑向管道2和管道3方向传播的水击,在分叉点处,管道1内的水击波传入管道2和管道3时,水击波大小变为ΔH,两者的差值ΔH0-ΔH为分叉点处产生的反弹水击波。
伴随着水击压力波动ΔH,存在一个流量波动ΔQ与之对应。在分叉点处,进入的流量波动为ΔQ,管道1中反弹回来的水击波对应的流量波动为ΔQ1,管道2中的流量波动为ΔQ2,管道3中的流量波动为ΔQ3。
根据茹科夫斯基关系式,压力波动与流量波动之间有
(2)
式中,A为管道截面积。
在分叉点处,根据流量守恒,有
ΔQ2+ΔQ3-ΔQ1=ΔQ
(3)
将式(2)代入式(3),有
(4)
将上式化简,有
(5)
即
(6)
定义衰减率δ为式(7)所示
δ=1-ΔH/ΔH0
(7)
由式(7)所示,衰减率主要受支管和干管管径比影响。图4所示为衰减率随管径比的变化规律。如图4所示,水击波在较粗管道(干管)上传播,遇到较细的分支(支管)时,水击波产生衰减,支管管径越细,衰减率δ越低。
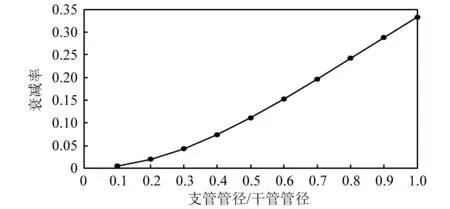
图4 干管向支管分支分流
(2)泄漏点位于支管
若泄漏点在支管上,则会出现支管向干管传播水击的情况,显然这样的分流也会存在显著的衰减效应。
如图5所示,当支管的管径是干管的0.5倍时,水击波衰减接近80%,而如果是干管向支管分流的话,同样支管的管径是干管的0.5倍时,水击波仅衰减10%左右。因此如果泄漏点在支管上,跨过干管后,压力波信号会严重衰减[16]。
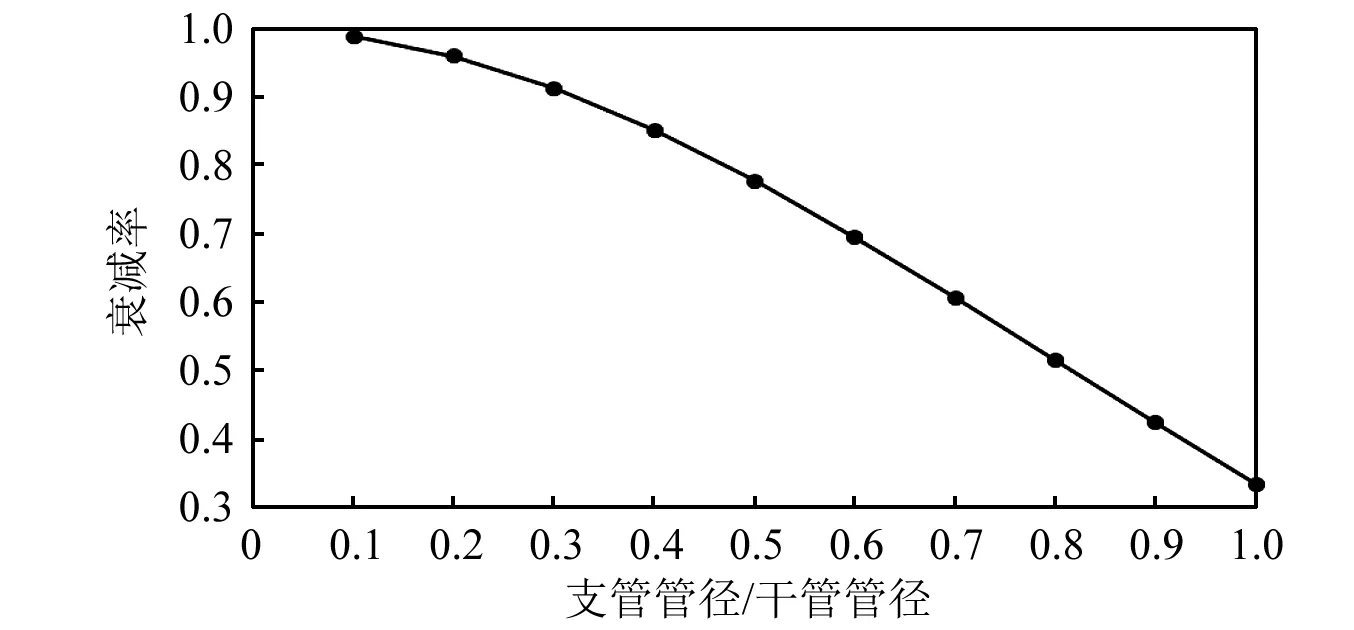
图5 水击波支管向干管分流
1.3 小波变换信号处理过程
小波分析不仅对严重泄漏时的压力信号可突出特征,而且对于轻微泄漏情况下或干扰作用下特征信息微弱的压力信号,具有很好的降噪[17]、特征提取的作用[18]。试验获得压力数据后,数据批量进入信号处理程序,数据的批量获取采用滑动窗口的方式,第一次运行时读取600个压力数据作为初始样本,之后每次读入500个数据和前一拍的后100个数据组成新的数据样本s。获得样本后,数据处理步骤如下:
步骤1对样本s采用db1小波变换进行滤波,得到滤波后的数据[a7],以及最后一层小波数据[d7]。
步骤2初步判断数据是否存在突变,具体方法为:对序列数据[a7],计算其峰谷比τ=max[a7]/min[a7]。若τ高于阈值τmax(阈值τmax可设置为1.05),则该段数据存在压力突变,转到步骤3;否则不进行后续操作,等待下次运行。
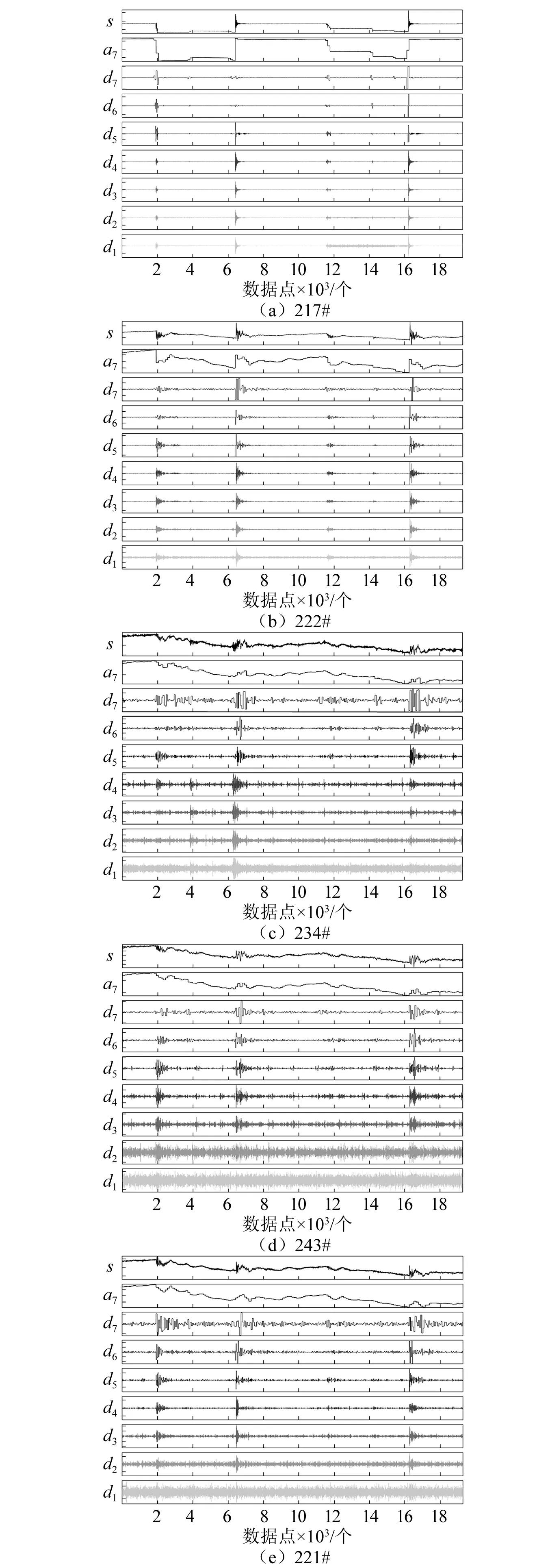
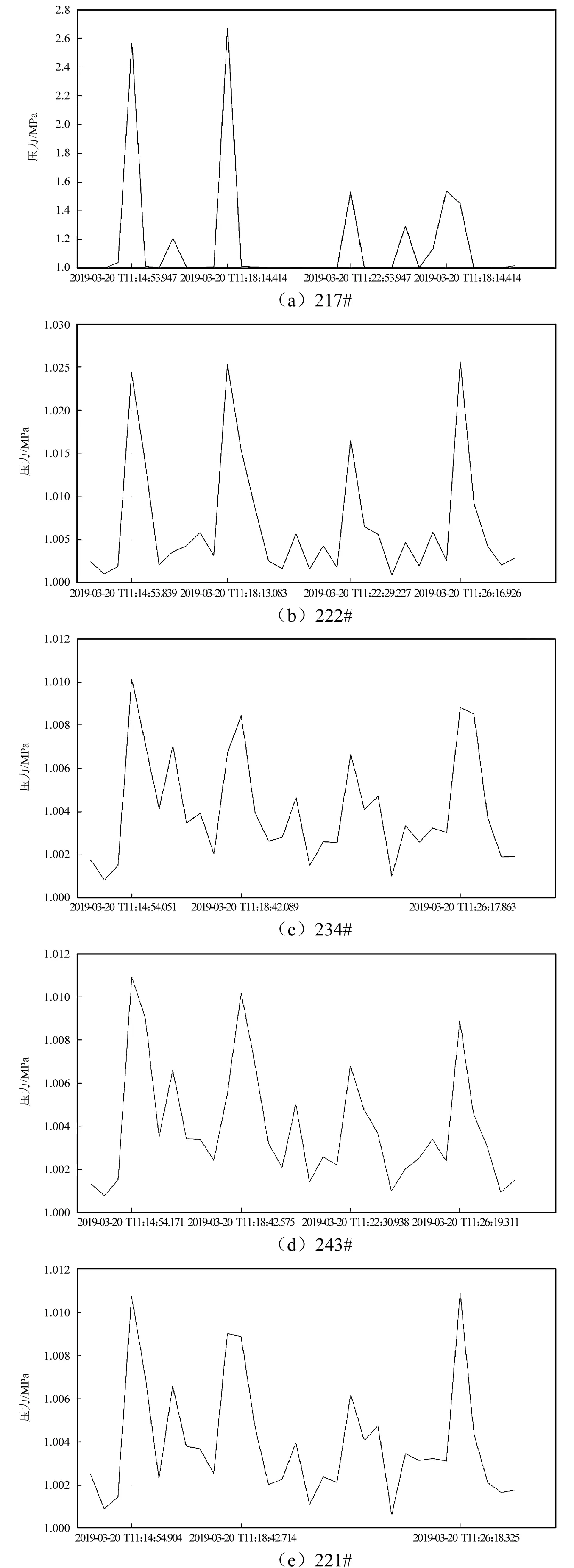
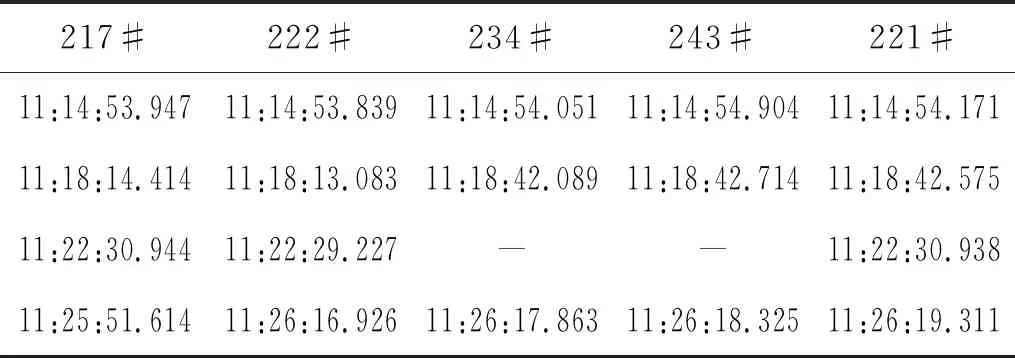
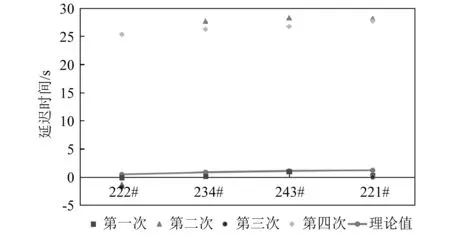
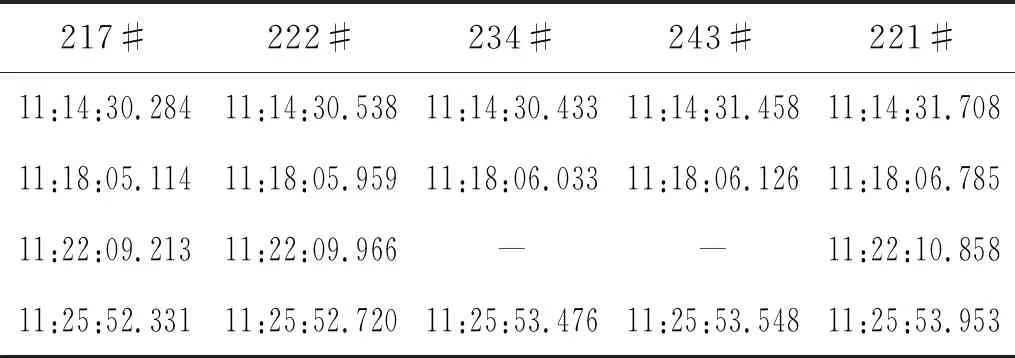
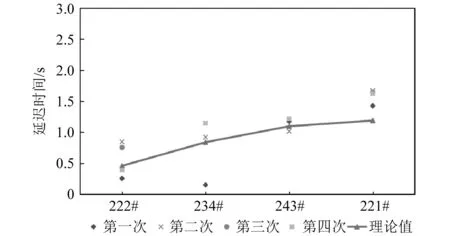
步骤3判断压力的变化趋势,将本次的最小值与上一拍数据的最小值作比较,若有min[a7]1 步骤4在样本s的基础上,补充上一拍的数据(500个点)得到s0-1,对s0-1采用db1小波变换滤波,得到[a7]0-1和[d7]0-1。 步骤5计算压力下降的幅值δ以及压力下降的百分比dec如下,作为判断是否泄漏的重要指标。 δ=max[a7]0-1-min[a7]0-1 (8) (9) 步骤6可进一步基于Mann-Kendall算法等,对序列数据[d7]0-1进行突变点检测,以确定突变发生的具体时间。 Mann-Kendall突变点检测算法步骤如下: 步骤1设原始时间序列为y1,y2,…,yn,mi表示第i个样本yi>yj(1≤j≤i)的累积数,定义统计量 (10) 步骤2在原序列随机独立等假设下,dk的均值和方差分别为 (11) 步骤3将上面公式的dk标准化,得 (12) 步骤4UFk组成一条UF曲线,通过信度检验可得出其是否有明显的变化趋势。 步骤5把此方法引用到反序列中,计算得到另一条曲线UB,则两条曲线在置信区间内的交点确定为突变点。 步骤6给定显著性水平α=0.05,则统计量UF和UB的临界值为±1.96。UF>0,表示序列呈上升趋势;反之,表明呈下降趋势,大于或小于±1.96,表示上升或下降趋势明显。 算法整体一次循环的流程图如图6所示。 图6 算法总流程图 选择某供热单位五座热力站的一次网压力作为测试对象,五座热力站分别为217#、222#、234#、243#和221#热力站,具体位置分布如图7所示,其中217#热力站为泄放热力站,用于模拟管线突发泄漏情况。217#热力站位于干管旁边,从217#热力站传出的压力波动信号会出现严重的衰减,因此可以通过此实验来分析分支衰减对信号监测与分析的影响。此外,为避免全网平衡及附近补水对压力信号的干扰,自控系统退出自动平衡并关闭周边热力站补水。 图7 待测试热力站平面图 根据图7所示平面图,可以测量沿途管道长度,并得到各监测热力站距217#热力站的距离。然后根据波速计算式(1)计算出各段管道波速,再根据波速和各管道长度计算出水击波传播到各监测热力站的延迟时间,结果如表1所示。 表1 监测热力站与实验热力站之间的路由距离与延迟时间 217#热力站为实验站,站内泄放点位置如图8所示,实验过程中,先关闭进出站球阀,打开除污器检查孔上球阀,利用除污器检查孔进行泄水。 图8 217#热力站泄放口 试验利用高频率(20 Hz)压力信号采集器监测一级管网泄漏时压力变化情况,并进行数据分析与比对,得到不同阀门开度下泄放时压力波变化情况。 具体试验操作如下:首先对五台压力采集器上电并连接热点进行校时,再将压力采集器探头连接在一级网就地压力表接口位置。在217#热力站站内进行排水试验,关闭供水进站阀门,出站阀门关至较小开度,操作除污器DN125排污球阀开度模拟泄漏工况状态。共计进行4次泄放实验,用压力采集器进行波形采集,四次操作如下所示: (1)泄放球阀全开,持续时间3 min后关闭; (2)泄放球阀1/4开度,持续时间2 min后关闭; (3)泄放球阀1/2开度,持续时间2 min后关闭; (4)泄放球阀3/4开度,持续时间2 min后关闭。 在测试过程中,为保证217#热力站中操作人员安全,关小了热力站的进出口阀门,以防止泄放球阀开启时水流过大发生危险,因此217#热力站中的压力测点为节流后的压力,导致图9中显示的测点压力波动非常大,而实际一次网的压力波动要比测点压力波动小很多。图10所示为实验过程中信号监测热力站的压力波动。由于各站同217#热力站的距离不同,因此压力波动开始的时间不同,并且由于压力波动先传播到DN1200的干管上,再传播到各自的支管上,因此压力波动衰减也很明显。实验测得的压力波动结果如图9和图10所示。 图9 217#热力站测点压力波动 图10 信号监测热力站测点压力波动 将图9与图10中展示的各热力站压力波动信号进行小波变换,结果如图11所示,其中:s=a7+d7+d6+d5+d4+d3+d2+d1。 图11 各热力站小波变换结果 利用1.3节中所述的信号处理方法,得到各热力站压力信号的峰谷比,如图12所示。 图12 各热力站峰谷比计算结果 峰谷比曲线中,根据压力波动的特征,最大峰谷比所对应的时间为潜在的时间指标,根据监测各站最大峰谷比所对应时间的延迟,也可能与水击波传播所产生的延迟时间相对应。 由上图可得,在泄漏点和监测点均存在压力信号的最大峰谷比出现时间和压力变化出现时间。下面对采用最大峰谷比出现的时间延迟和压力变化出现的时间延迟作为指标,对水击波传播所产生的延迟时间进行估算的有效性进行分析。 首先,对采用压力信号最大峰谷比为指标的有效性进行分析。各站压力波动的最大峰谷比所对应的时间,如表2所示。由于234#热力站和243#热力站在第三组实验中的最大峰谷比峰值过小,因此算法没有抓取出来。 表2 最大峰谷比时间 将表2中222#热力站、234#热力站、243#热力站以及221#热力站的最大峰谷比时间减去对应的217#热力站最大峰谷比时间,得到每组实验对应的时间延迟,对比最大峰谷比时间延迟与水击波传播理论时间延迟,如图13所示。由图可知,最大峰谷比时间的延迟要远大于理论时间延迟。误差约为半分钟左右,换算到距离则为30 km左右,完全无法起到定位的作用。因此无法利用最大峰谷比指标进行定位。 图13 最大峰谷比延迟时间与理论延迟时间对比 采用1.3节中的算法,可以计算出各监测热力站压力变化时间,如表3所示。同样的,由于第三组实验中的234#热力站与243#热力站最大峰谷比时间没有抓出来,因此压力变化时间也空缺。 表3 压力变化时间 同样的,将表3中222#、234#、243#以及221#热力站的压力变化时间减去对应的217#热力站压力变化时间,得到每组实验对应的时间延迟。图14所示为实际压力变化时间延迟与理论时间延迟。图中可得,除第一次实验的234#站的数据以外,通过数据处理算法得到的压力变化时间延迟与理论时间延迟误差保持在1 s以内。因此,该指标可将泄漏点位置缩小到1 km范围内,起到有效的定位效果。 图14 压力变化延迟时间与理论延迟时间对比 由于集中供热管网存在大量的分支,因此将负压波方法应用到供热管网会出现严重的衰减,会导致位于热力站的监测点压力波动太小而无法定位。因此,热网中设置监测点时需要考虑热网的拓扑结构,使得监测点可以覆盖到绝大部分管网。本文通过实际管网泄漏实验,测试泄漏点和监测点的压力变化,并利用小波变换的方法进行数据处理,探索负压波方法在供热管网中应用的可行性。结论如下: (1)采用最大峰谷比延迟时间为指标,无法有效估计水击波的传播时间差,文中的测试工况下,最大的误差在30 s左右,泄漏点定位误差则在30 km左右,无法在实践中采用; (2)而采用压力变化时间延迟作为指标,可以更有效估计水击波传播时间差,文中测试工况下,误差在1 s以内,泄漏点定位误差在1 km范围内,适合在实践中采用; (3)文中提出的信号处理方法能够有效的抓到压力变化的时间点,成功利用监测点信号降低定位误差距离,极大的提高泄漏点定位效率,具有重要的实际应用价值。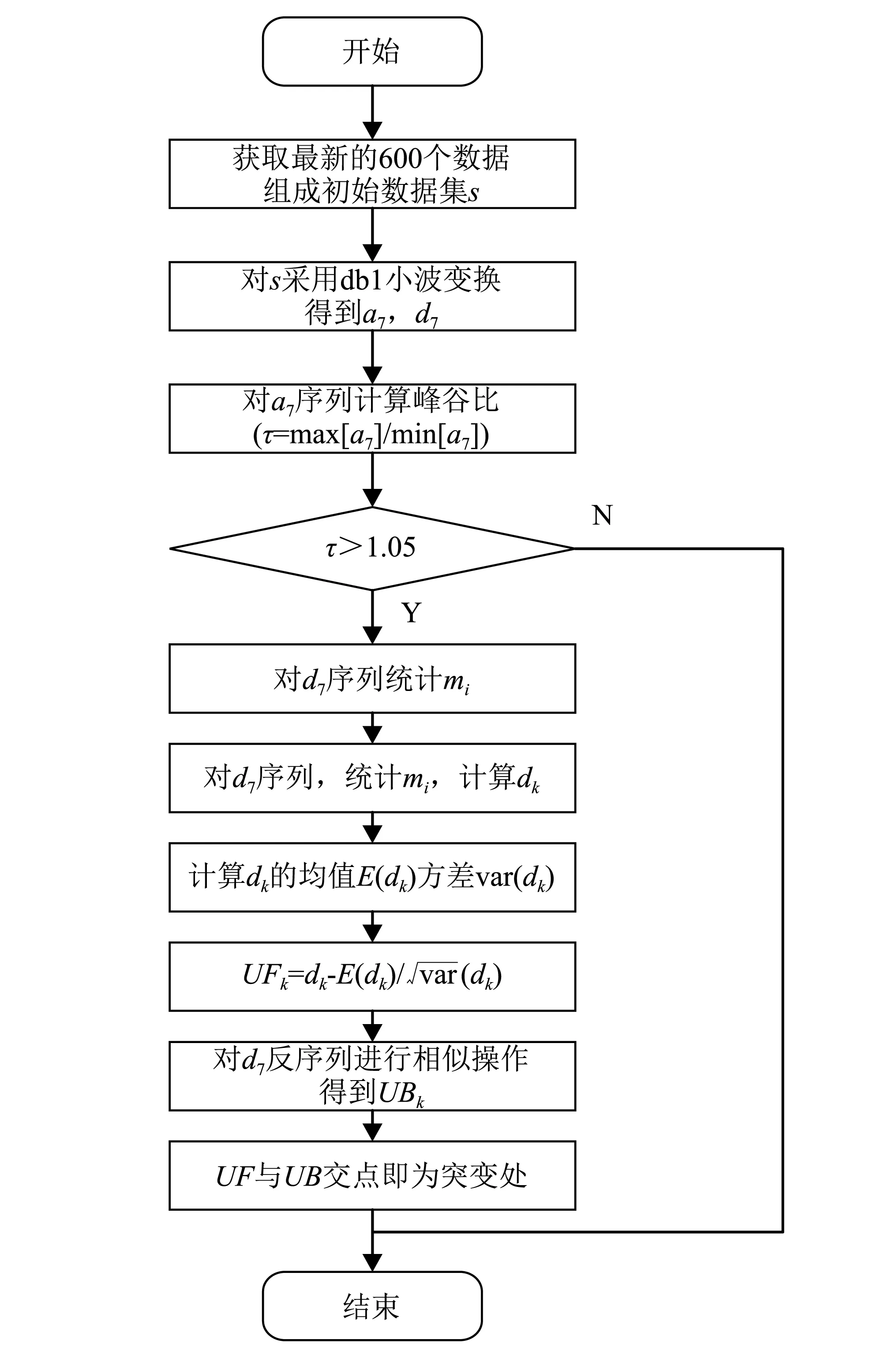
2 实验系统与实验过程
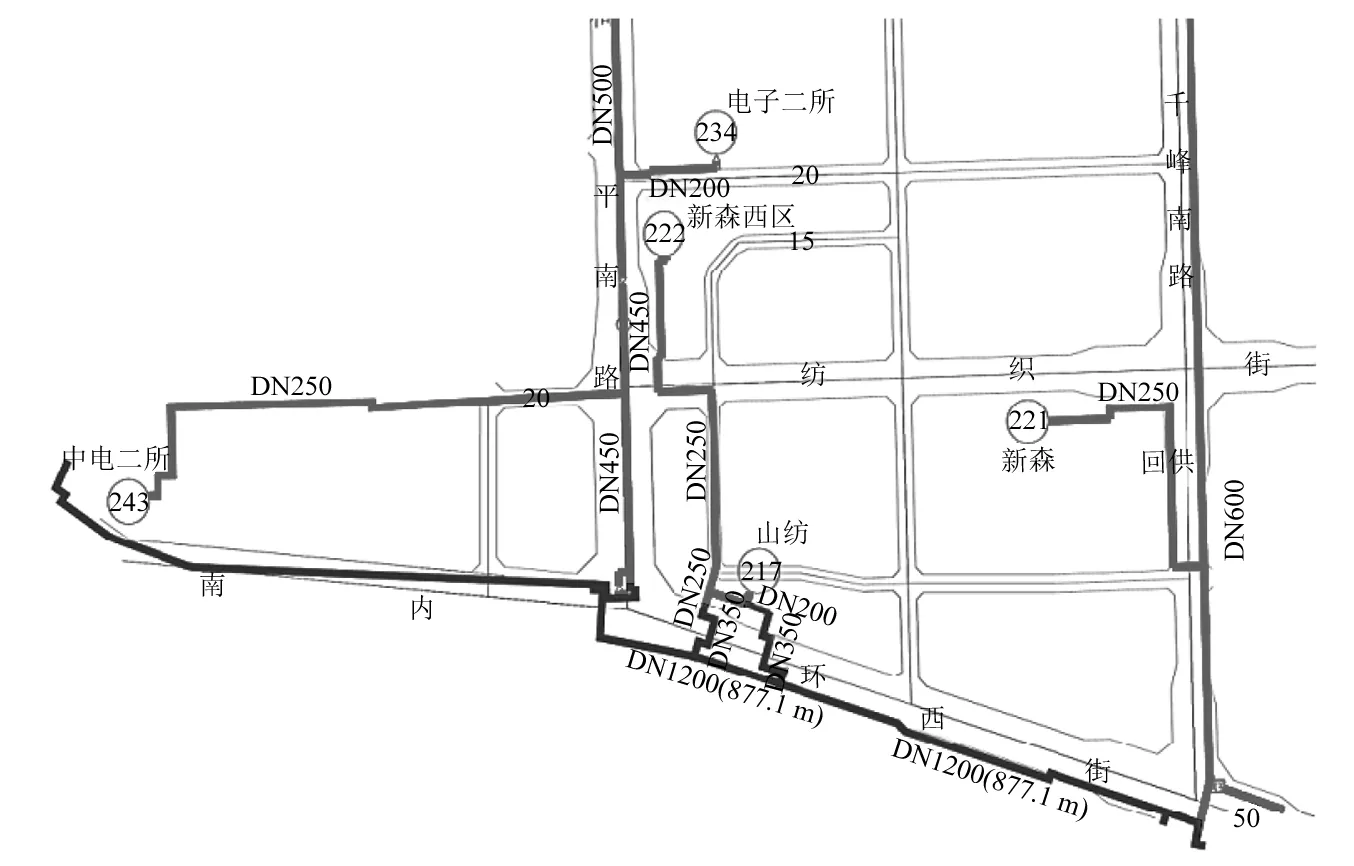


3 结果与讨论
3.1 实验结果与数据处理
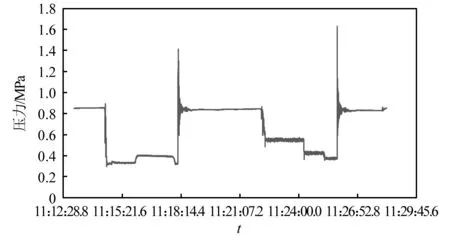
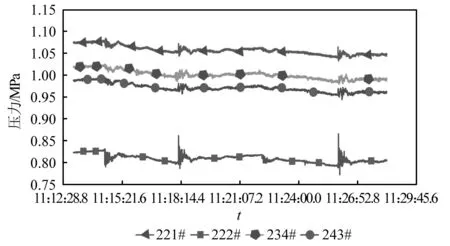
3.2 最大峰谷比延迟时间为指标的有效性分析
3.3 压力变化延迟时间为指标的有效性分析
4 结 论
