土体中岩石破坏次声波的三维多测点振速矢量直线汇聚声源定位方法

2021-07-22赵久彬刘元雪杨骏堂何少其

振动与冲击 2021年14期

赵久彬，刘元雪，柏准，杨骏堂，何少其

(1. 陆军勤务学院军事设施系，重庆 401311； 2. 岩土力学与地质环境保护重庆市重点实验室，重庆 401311)

滑坡泥石流等地质灾害发生前，岩石的爆裂、摩擦和断裂等破坏会产生低频的次声波[1-2]，由于次声波长较长频率低的特点，使其能够在传播中衰减少、抗干扰能力和穿透能力较强，这些优势使得次声波能够远距离传输，可以不考虑次声传感器和被测物体的耦合性。次声波的监测技术在地质灾害领域的研究,主要采用声发射技术、小波变换、小波包变换、时频分析等信号处理方法对次声信号的相对能量、频率等频谱和时频特征进行分析，获取出地质灾害发生前次声信号的重要特征，为地质灾害监测预警前兆特征所参考[3]。由于次声信号传播距离远衰减少，用在地质灾害发生地点的定位预测显得格外有应用价值，但国内外对次声波定位的研究还很少。

由于军事应用和海洋探测等领域的发展需求，声源定位在海洋水声定位的研究比较深入，声源定位技术从传统的时延算法[4-5]、波束形成算法[6-7]，向更加精确的匹配场[8-9]算法发展。但是在陆地的微震、泥石流、滑坡等声波定位技术研究领域，还停留在室内试验阶段[10]，黄晓红等[11]采用在室内岩土试块内激发超声信号，通过部署在表面的传感器收集信号，采用时延算法进行声发射定位。对于岩石破坏的次声信号研究，在信号处理领域的定位方法和声场传播理论方面还有很大的研究空间。

本文首先分析滑坡泥石流等地质灾害中，灾害发生前夕由于岩石破坏产生次声波机理，通过数值模拟发现土体中爆炸发出的次声波的频率范围与岩石破坏的次声波频率范围相当，可以通过该方法呈现出岩石破坏产生次声波现象，使次声波在土体及空气中传播。通过多个位于声场中的次声传感器监测点接收信号，基于测点振速矢量指向声源的原理，提出一种三维多测点振速矢量直线汇聚次声声源定位方法，作为初步展示，采用数值模拟的方法建立土质滑坡模型和土壤空气分层介质模型中发出次声信号，在模型体中部署3个次声传感器收集信号，采用三维多测点振速矢量直线汇集次声声源定位方法，准确获得了声源坐标位置。

1 岩石破坏产生次声波机理及数值模拟

1.1 岩石破坏产生次声波机理

国内外学者通过长期观测和试验发现，岩石结构从裂纹产生、贯通和破坏过程中能够辐射出声波[12-17]。当岩石结构处于非稳定平衡状态时，岩石内部产生微观下晶体之间的破裂和拓展，形成能量的积累。当能量积累到临界值时岩石爆炸释放能量产生应力波，形成声发射。岩石破坏过程中的声发射会产生高频和低频声波。高频声波由于频率高衰减很快，无法进行远距离传播，监测设备不能接收到信号。而低频信号尤其是次声波具有频率低衰减少的特点，可以进行远距离传播。由于岩体的声发射是滑坡崩塌等地质灾害临发的重要标志，可以对灾害体进行次声波监测，通过数学建模方法进行灾害发生地点进行定位，从而实现提前灾害预警[18]。

国内外很多学者通过岩石破坏试验收集次声波特征，发现岩石破坏次声波异常信号能量主要集中在3.19～7.81 Hz内，而在岩土体爆炸与冲击工程中，冲击波引发和衰减形成次声波在远距离传播，收集的次声波信号的次声能量集中在2～8 Hz。由于在地质环境中实施土体岩石破坏试验难度较大，可以在岩土体中设置小当量炸药爆炸，模拟地质灾害中岩石破坏产生的次声现象，研究次声定位方法。初期我们采用数值模拟方法，提出一种三维多测点振速矢量直线汇聚次声声源定位方法。

1.2 数值模型的建立

本文设计的模型一共有土体和炸药两部分。土体的尺寸为8 000 m×8 000 m×8 000 m，模拟岩石爆裂的小当量炸药尺寸为边长75 m×75 m×75 m的立方体，将其安放在土体中心，模拟地质灾害发生前，岩石挤压爆裂产生次声波的现象[19]，如图1所示。采用LS-DYNA程序中的多物质ALE算法模拟岩石爆裂体爆炸后冲击波传播及土介质的运动[20]。

图1 立方体1/8网格模型

选用SOLID164实体进行网格划分，由于模型是全对称结构，故可分析模型的1/8结构，共有243 085个单元，250 047个节点。土体和岩石爆裂体采用映射方法划分网格，其中土体采用非等距离划分方法，距离中心近密远疏，岩石爆裂体采用小剂量TNT炸药材料替代。为了模拟出无限的土体区域，模型边界均采用透射条件，选择炸药材料模型MAT_HIGH_EXPLOSIVE_BURN和EOS_JWL关键字为岩石爆裂体中炸药的材料模型和状态方程，土体选用土壤泡沫材料模型MAT_SOIL_AND_FOAM关键字。模型外界边界执行零位移全约束，数值模拟采用单位为m-kg-μs建模，计算时间为300 s,每3.6 s提取一次数据，计算生成K文件进行显示动力运算。

1.3 标准计算结果

岩石爆裂体中爆炸发生后，产生巨大的能量释放，形成球形冲击波向外在土体中传播，冲击波的能量很大频率很高，在土体介质中衰减很快，衰减形成较低频率的压力波继续向外传播[21]。如图2所示为爆炸过程中土体结构在不同时刻的等值压力图:图2(a)为发生爆炸时刻；图2(b)说明爆炸后冲击波以球面波形式向外扩大，球形冲击波向外传播形成更大的球面波，最外层能量最小，最里层能量最大，说明在传播过程中发生能量衰减；如图2(c)所示，在球面冲击波向外传播的同时，内部出现了形状犹如“水花”的压力波，继而新的冲击波再次被激发，形成球形冲击波线外传播，但是第二轮冲击波的能量较第一次低，形成了能量层次为“低-中-低”组成的球形波向外传播；接着在中心再次产生了能量很低的压力波，如图2(d)所示，产生的冲击波在中心形成涟漪，由于能量很低已经无法向外传播；最后如图2(e)所示，之前形成的层次为“低-中-低”能量的球形波最终衰减为能量低的压力波，可以传播到很远的距离而不衰减，这说明此种压力波具有频率低、衰减小、传播远的特征，说明产生了次声波向外传播；传播最终达到模型边界，由于边界设置为透射条件，次声波向外透射继续传播，如图2(f)所示。

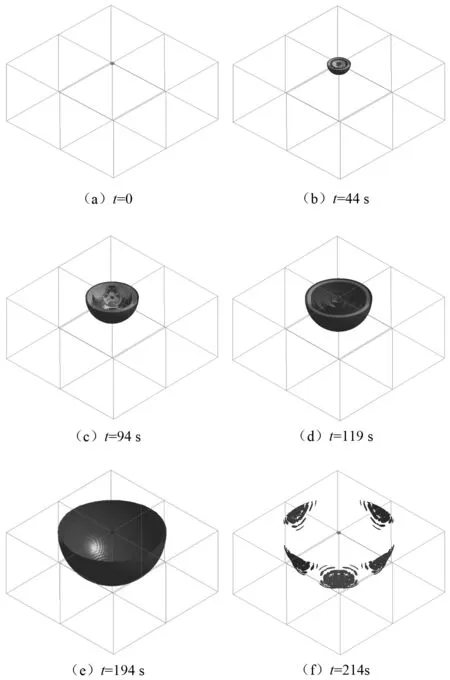
图2 各时刻1/2面的等值压力图

1.4 各测点的信号压力和振速矢量信号分析

为了了解土体中不同区域中受冲击波影响的作用，设置3个不同位置的监测点，其单元编号及坐标为A455(2 575.3,0,0)，A4024(1 588.42,0,1 782.23)，A13046(1 525.80,845.52,0)，如图3所示为3个监测点的单元位置,分别设置在爆裂点的正上方、左方较远位置和右方较近位置，以便于比较各个不同特征位置接收到的应力波信号异同。图4为在爆裂期间3个监测点接收到的应力波变化曲线图，从图中我们可以发现，应力波首先到达距离爆裂点最近的A13046监测点，随后分别达到距离较远的A4024和A455监测点，3个监测点接收到的第一轮应力波能量最大，随后减小。

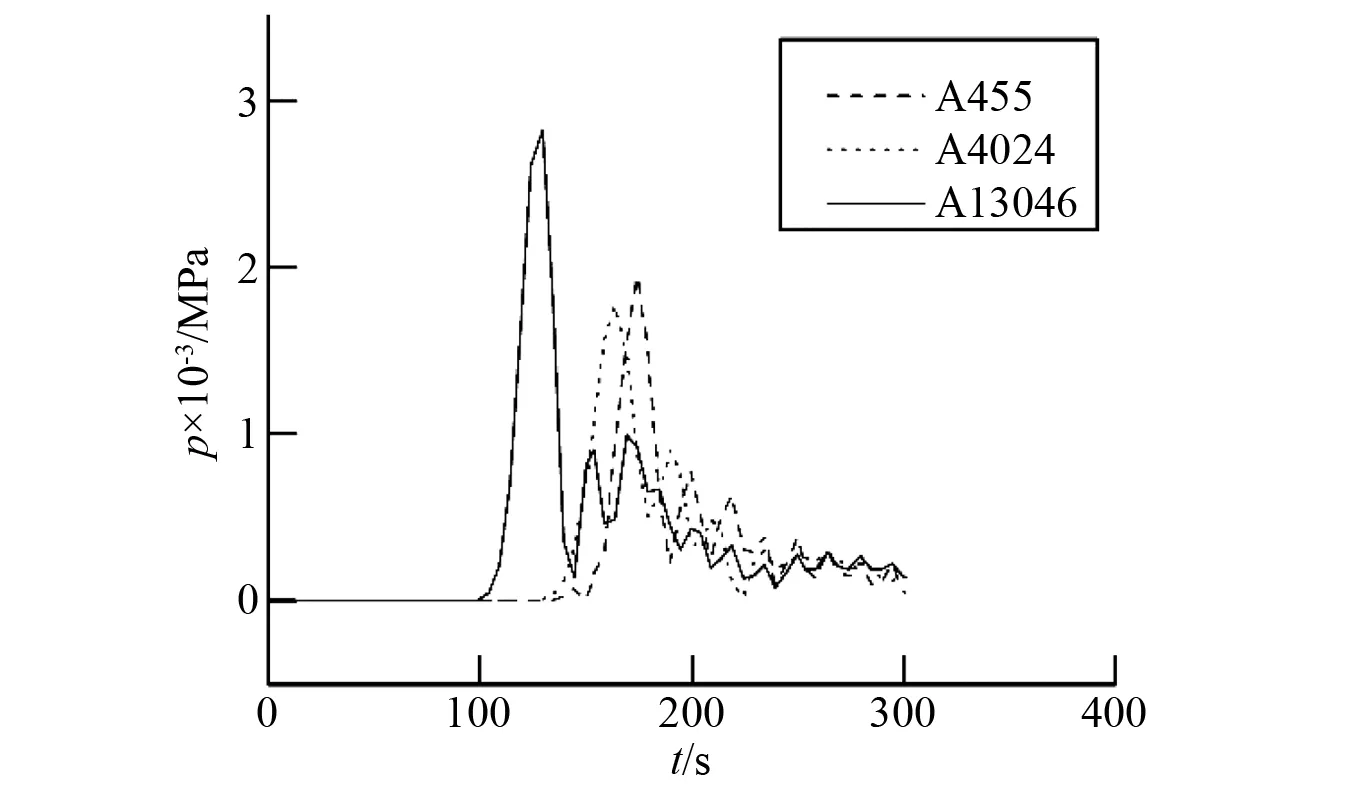
图4 各监测点压力

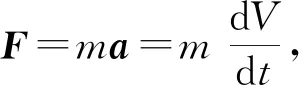
图5 A4024单元压力与各向质点振速对比图

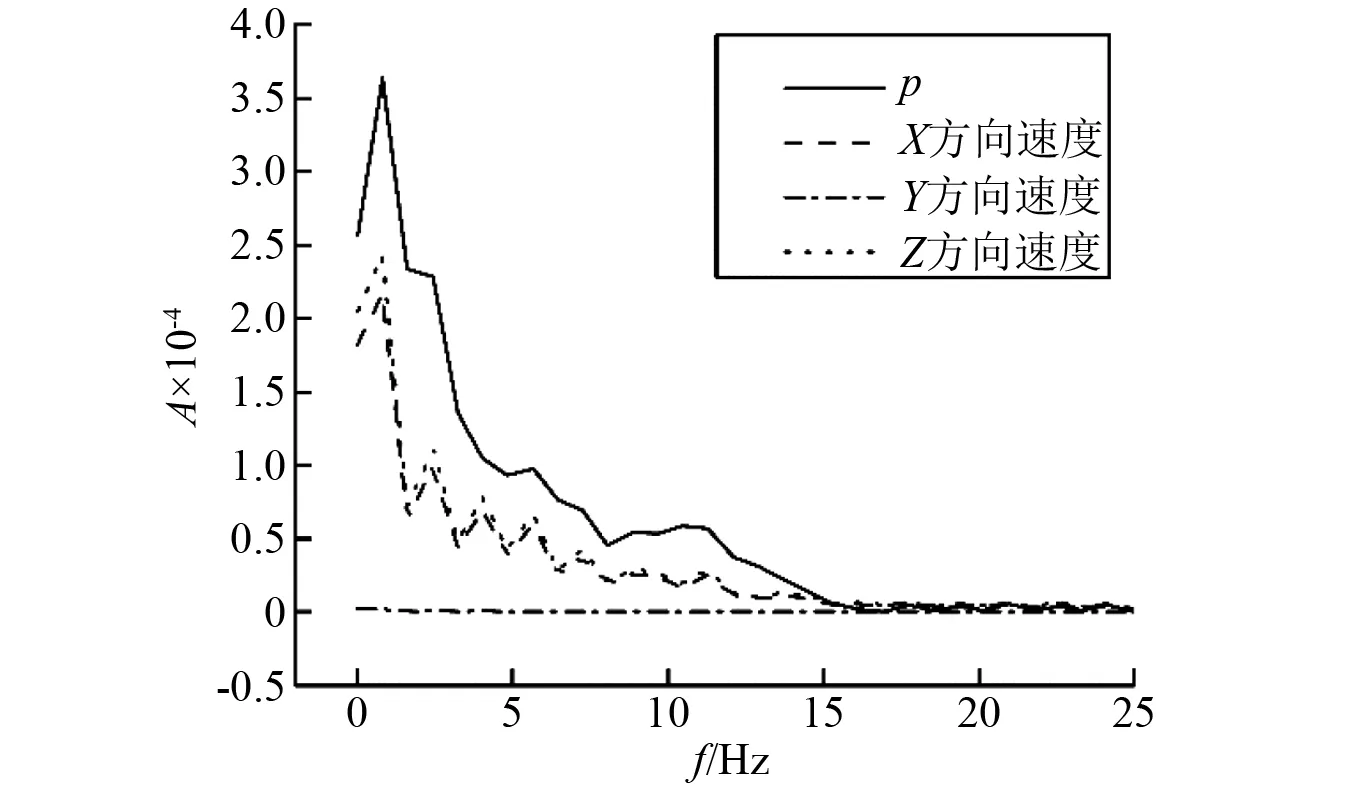
图6 A4024单元压力和质点振速频谱图

2 次声波传播模型及定位方法

2.1 次声波的多径传播模型

我们建立二维声场模型，其中土层尺寸为8 000 m×4 000 m，土壤的参数为：ρ=1 500 kg/m3,cp=1 500 m/s。采用声场传播仿真软件BELLHOP[22]，在MATLAB软件进行在次声波多径传播仿真，如图7所示。由文献[23]知土壤的剪切波传播速度为cs≤200 m/s，远远小于纵波速度，且在土质中衰减较快，当纵波到达时剪切波还未到达，故能在声波信号中明确辨别，所以本文不考虑土层的剪切波作用。次声源向接收点方向发出多条路径的次声波，其中直线传播路径为直达波，声能损耗最小，其余路径与上界面和下界面均发生了发射，其声能将发生较大损耗。从图中可以看到直达波与接收点的路径最短，故直达波最先达到接收点，由于直达波声能在所有声线中最大，且最早到达接收点，所以在接收传感器中的信号序列中，第一个声压波峰即为直达波的声压。

图7 次声波多径传播模型

根据文献[24]，当在弹性介质中不考虑剪切波时，其点声源存在速度势函数为

(1)

质点的各向振速为

(2)

由于各质点振速分量为速度势函数的导数，与时间因子无关，所以各质点振速分量应同时达到最值。由于直达波声线传播路径最短，传播时间最小，且声能损失最小，在接收点振速信号中第一个最大波峰即为直达波信号，本文采用该信号进行多测点振速矢量直线汇聚定位计算。

2.2 三维多测点振速矢量直线汇聚次声声源定位方法

岩石破坏产生的冲击波可视为一种应力弹性波，向外传播后衰减形成次声波向外继续传播[25]。由于应力的方向与振速的方向具有一致性，在介质中次声波到达某质点时，打破了该质点的静力平衡，其增加的最大的应力方向即为振速最大的方向，也是纵波的传播方向。本文提出一种三维多测点几何定位声源方法，以三测点为例。

在声场中布置3个不共面不共线测点，其位置分别为P1(x1,y1,z1)，P2(x2,y2,z2)，P3(x3,y3,z3)，为了测得次声波到达此点在各个方向引起的质点运动情况，测得3个测点的最大振速为V1(p1,q1,r1)，V2(p2,q2,r2)，V3(p3,q3,r3)，故其振速的方向矢量分别为

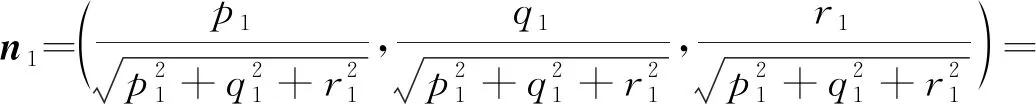
(3)

设L1，L2，L3分别为经过测点且其法线为方向矢量的直线方程，其形式为

(4)

由于所考虑声波为直线传播，在不考虑声波的折射和反射等影响下，上述三条振速矢量直线方程理论上的交点则为声源所在点，但实际中存在测量误差、折射等影响因素，往往三条振速矢量直线不能交于一点，但一定会向一个区域内聚集。如图8所示，线段AB垂直于直线L1与直线L2，也是L1与L2两直线间最短距离，若由直线L1与直线L2确定声源预测点，则线段AB中点O′12(x12,y12,z12)为最优预测点，证明如下：

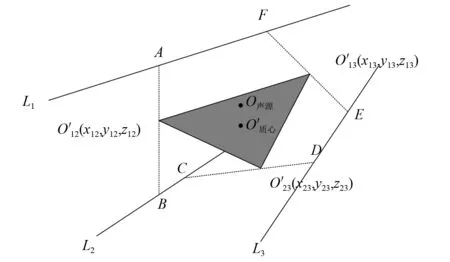
图8 三测点振速矢量直线汇聚于声源点

由于声源在线段AB上任意点出现的概率相等，那么需要在AB线段上寻找一点Q(xQ,yQ,zQ)，该点与其他点的距离总和最小时，则出现声源的概率最大。采用函数最值法求解，设AB长度为L，取目标函数数D(xQ,yQ,zQ)，为Q点与其他点距离平方的总和，则其表达式为

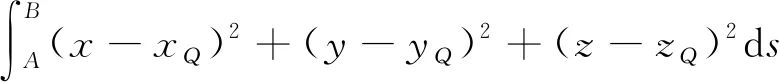
(5)

对其偏微分得

(6)

令式(6)中方程式为0，得到

(7)

式(7)表明，当线段AB为均值密度时，Q(xQ,yQ,zQ)的坐标为线段AB的质心，也就是AB的中点，那么对于由直线L1与直线L2确定的最优声源预测点为线段AB的中点，该点坐标为O′12(x12,y12,z12)。

同理，线段CD垂直于直线L2与直线L3，确定的最有声源预测点坐标为O′23(x23,y23,z23)；线段EF垂直于直线L1与直线L3，确定的最优声源预测点坐标为O′13(x13,y13,z13)。所以，上述的聚集区域就为由O′12，O′23，O′13组成的三角形，真实声源将出现在该三角区域中，按照上述函数最值法同样可以证明，三角形的质心O′与其他点的距离总和最小，故将质心坐标作为声源预测点的概率最大。则三测点振速矢量直线的声源点定位点坐标为

(8)

波导环境中的密度变化会影响该三角区域的大小，例如：当接收器位于声速较小，次声源位于声速较大的波导环境中，其定位的三角区域会增大；当接收器位于声速较大，次声源位于声速较小的波导环境中，其定位的三角区域会减小。由于本文的定位算法基于概率和统计优化的数学原理，可以有效减少由于界面密度变化产生的定位误差，在应对不同介质之间传播定位具有适用性。

以上为本文提出的三维多测点多振速矢量直线汇聚次声声源定位方法，下面以1.2节建立的模型具体说明。选取该模型的单元编号为A13046，A4024，A455三点进行验证该算法。如图9～图11所示为各个质点的振速变化图，可知A455监测点的振速最大值V1(0.001 174 62,06.35×10-6,6.37×10-6)m/s，A4024监测点的振速最大值为V2(0.000 803 095,0.000 009 69,0.000 900 883)m/s，A13046监测点的振速最大值为V3(0.001 488 24，0.000 836 661，0.000 018 1)m/s。根据式(4)求出三条经过测点且指向声源方向的直线方程如图12所示，其形式为

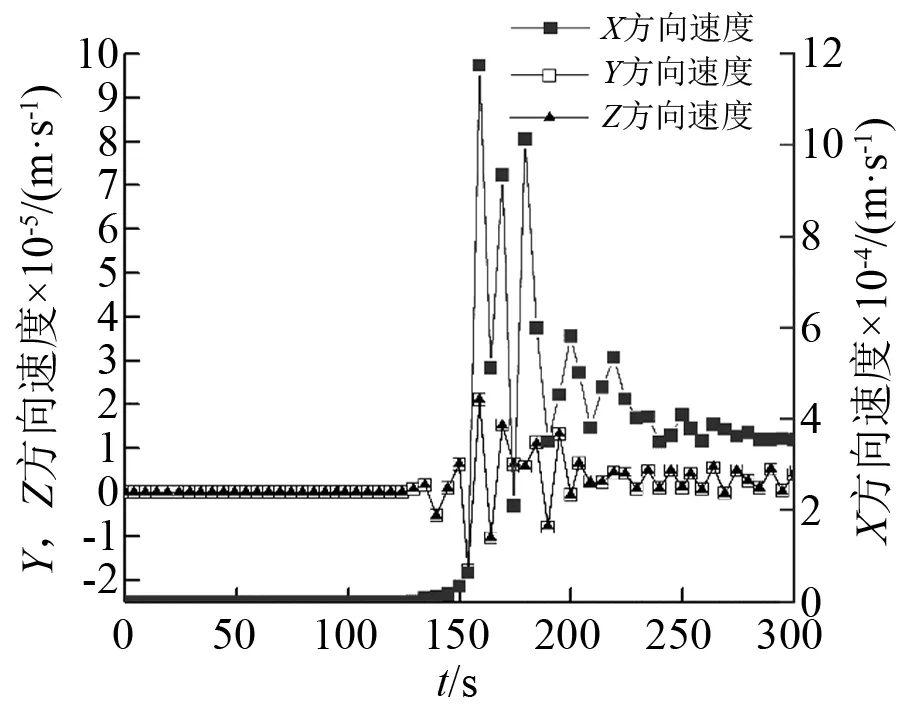
图9 A455监测点各向振速

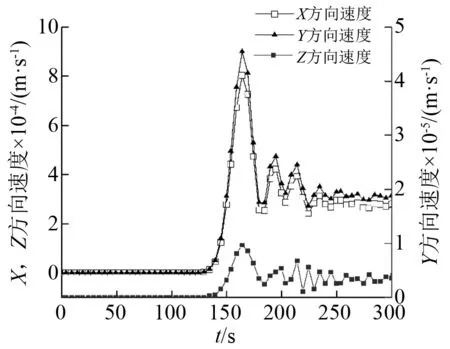
图10 A4024监测点各向振速

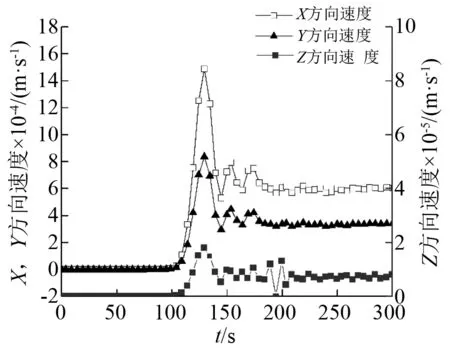
图11 A13046监测点各向振速

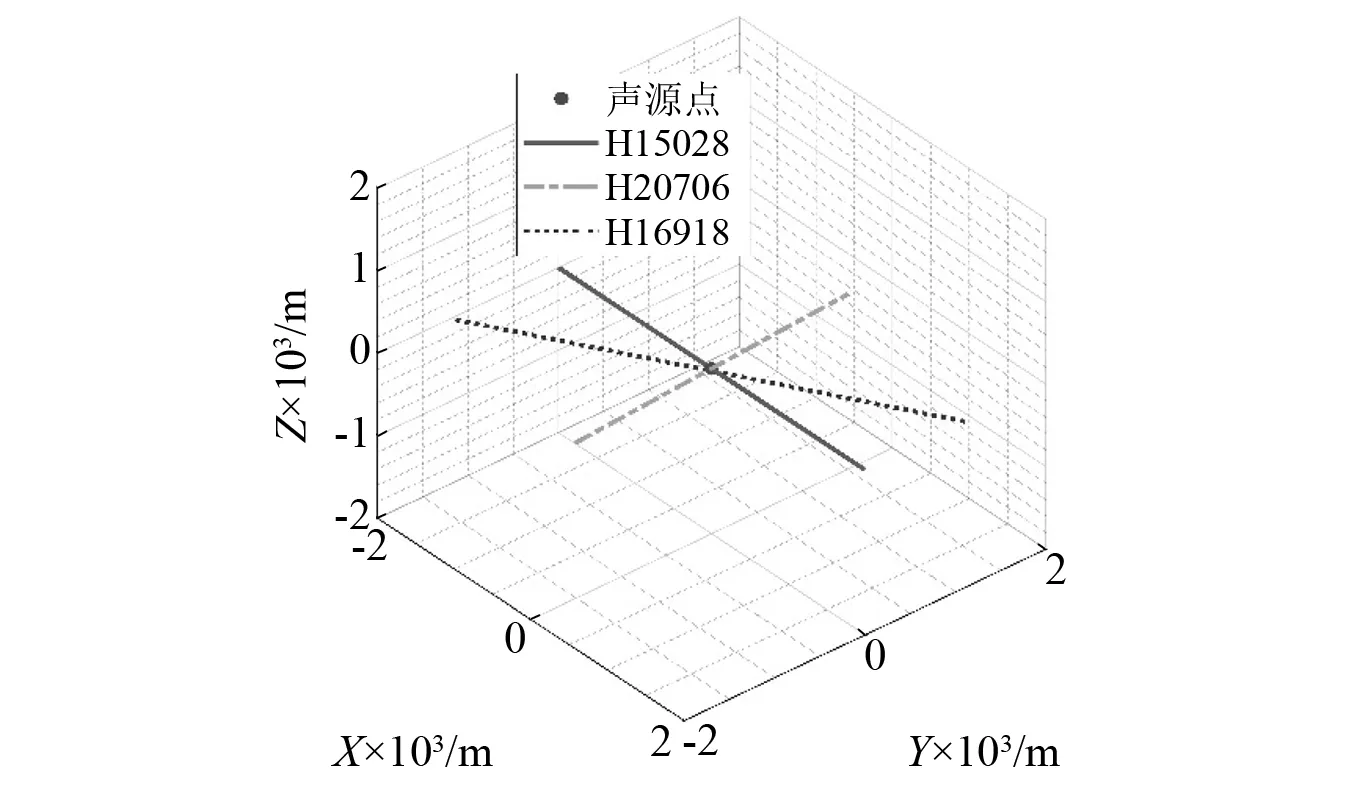
图12 模型中三测点直线汇聚示意图

(9)

根据上述方法，求出各坐标点如表1所示。其中：O点为爆裂点，为所建模型的原点；O′为本文提供的声源定位方法所得的声源坐标，发现该坐标位置在爆裂模型内，结果表明该方法预测出的声源位置位于岩爆体内，且圆概率误差仅有8.09 m，这个误差在地质灾害监测预警工程中，是可以接受的。

表1 三测点定位坐标

3 数值模拟验证

3.1 土质滑坡

为了验证该定位方法的有效性，本文建立实体土质滑坡爆炸模型。某一处土质滑坡，其尺寸如图13所示，其爆裂体中炸药尺寸为6 m×6 m×6 m，采用LS-DYNA程序中的多物质ALE算法模拟爆裂后次声波的传播运动。其数值模拟方法和参数与1.2节方法一致。

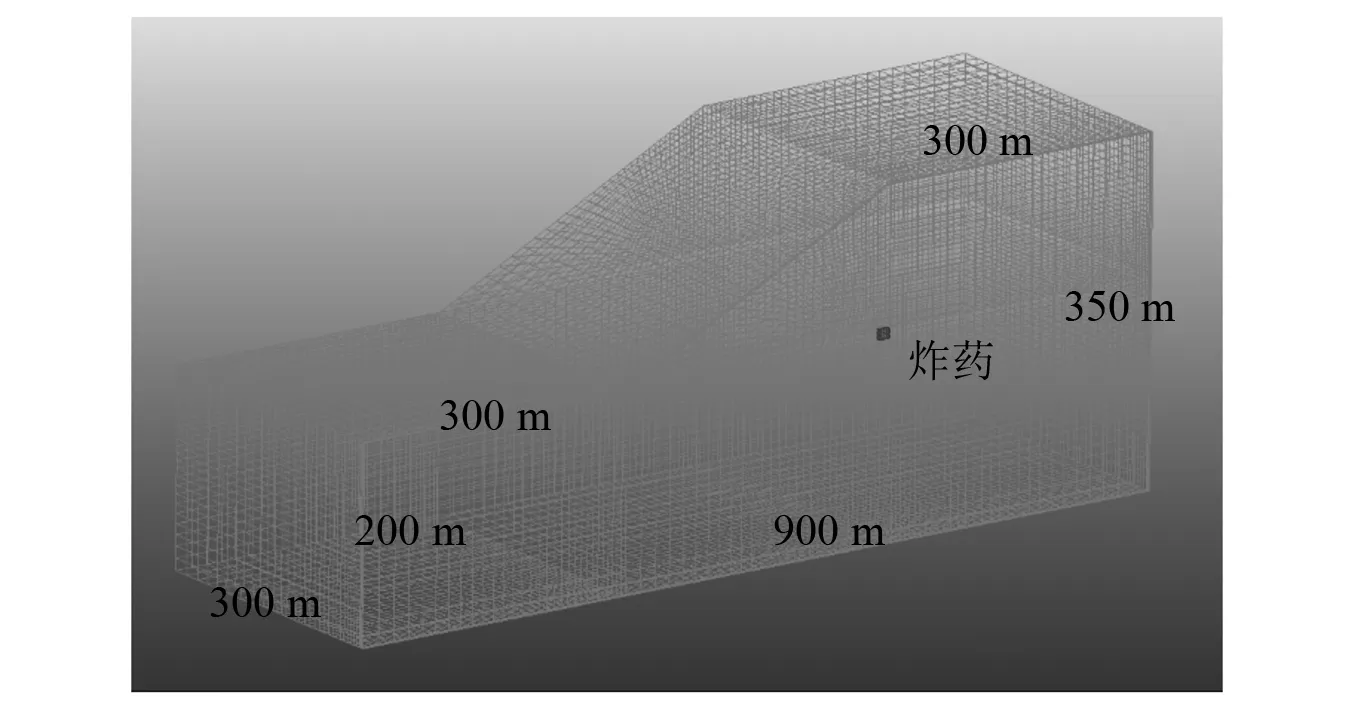
图13 土质滑坡1/2网格模型

按照上述方法，为便于施工方便，在滑坡体的表面任意选择3个地点安装次声波传感器，收集当地的各向质点振速信号。为便于叙述，本文选择了如下地点如图14所示，其单元编号及坐标为H15028(218.30,40.85,101.77)m，H20706(38.06,130.97,9.52)m，H16918(115.93,92.03,203.42)m，以便于比较各个不同特征位置接收到的应力波信号异同。

图14 土质滑坡次声传感器所在位置

分析得到H15028监测点的振速最大值V1(0.000 143 017, 2.93×10-5, 6.25×10-5)m/s，H20706监测点的振速最大值为V2(0.000 123 284, 0.000 485 8, 3.07×10-5)m/s，H16918监测点的振速最大值为V3(4.76×10-5, 3.86×10-5, 8.54×10-5)m/s。求出三条经过测点且指向声源方向的直线方程如下，其空间位置如图15所示。

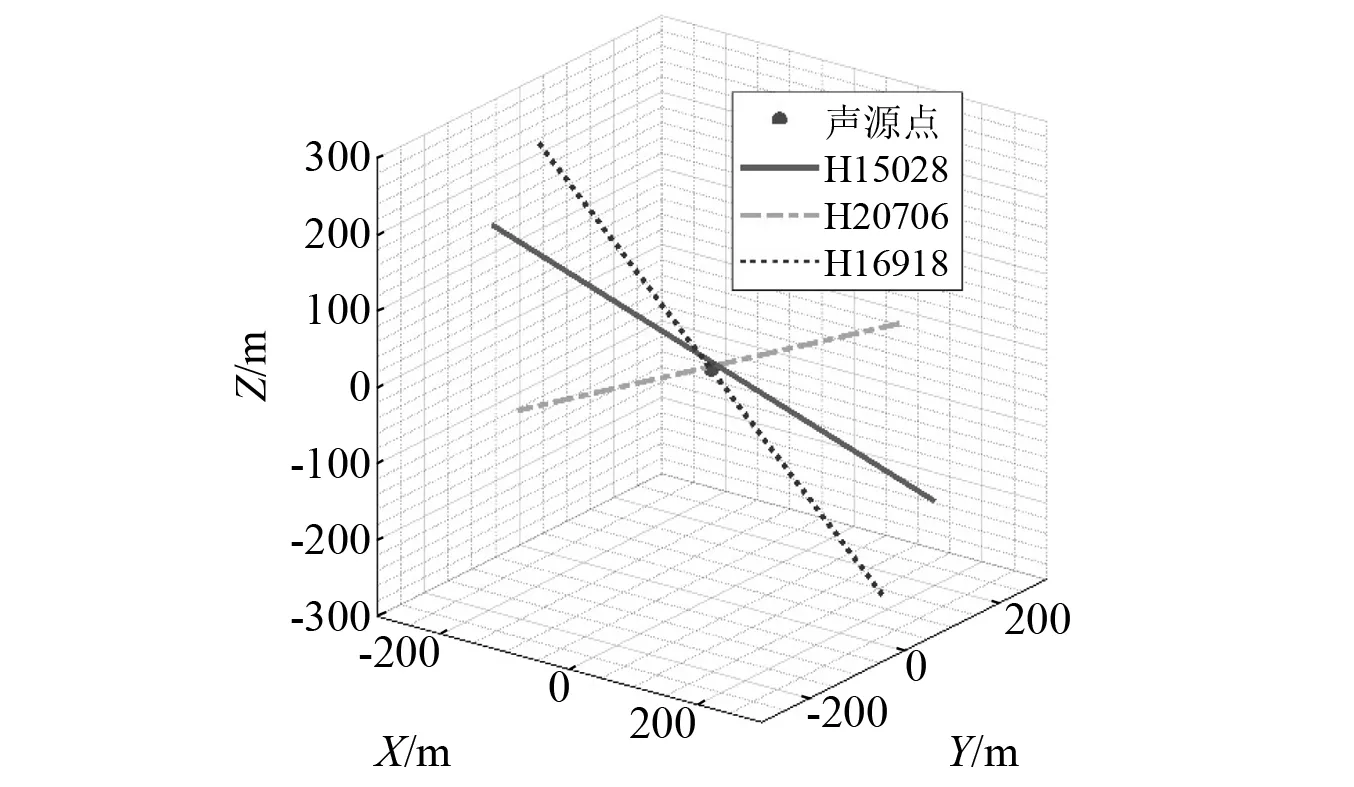
图15 滑坡模型中三测点直线汇聚示意图

(10)

根据本文提出的方法，求出各坐标点如表2所示。其中：R点为爆裂点，为所建模型的原点；R′为本文提供的声源定位方法所得的声源坐标，发现该坐标位置在爆裂模型内，结果表明该方法预测出的声源位置位于岩爆体内，且圆概率误差仅有5.11 m，这个误差在地质灾害监测预警工程中，说明该算法能够精确定位，应用于灾害监测预警具有广阔前景。

表2 滑坡模型中三测点定位坐标

3.2 土壤和空气不同介质

声波从介质向另一种介质传播将发生反射和透射现象，其规律满足斯涅尔定律。实际的岩土体的局部破坏发生在岩土层中，次声波将从岩土层中透射到空气中。为探究声源定位方法在在不同介质中应用的定位效果和误差，我们建立了土壤-空气分层模型。其尺寸如图16所示，其中爆裂体中炸药尺寸为6 m×6 m×6 m，采用LS-DYNA程序中的多物质ALE算法模拟爆裂后次声波的传播运动。其数值模拟方法和参数与土质滑坡模型一致。

图16 土壤和空气的1/4模型

选择测点如图17所示，其单元编号及坐标为A958549(3,93,18)m，A961489(3,57,90)m，A529488(51,54,3)m，以便于比较各个不同特征位置接收到的应力波信号异同。各监测位置收集到传感器的各向振速数据，分析得到A958549监测点的振速最大值V1(5.47×10-17, 1.51×10-15, 3.7×10-16)m/s，A962351监测点的振速最大值为V2(3.808 76×10-9,7.917 39×10-8,1.326 95×10-7)m/s，A529488监测点的振速最大值为V3(0.000 049 8,0.000 056 7,0.000 003 53)m/s。求出三条经过测点且指向声源方向的直线方程如下，其空间位置如图18所示。

图18 不同介质模型中三测点直线汇聚示意图

(11)

根据本文提出的方法，求出各坐标点如表3所示，其中：P点为爆裂点，为所建模型的原点；P′为本文提供的声源定位方法所得的声源坐标，结果表明该方法预测出的声源位置位于岩爆体内，且圆概率误差仅有4.04 m。为了比较本文定位方法在不同介质中的定位效果，我们以最远测点的距离为基准，比较土质滑坡模型与不同介质模型定位误差。土质滑坡的定位误差为2.03%，而不同介质模型定位误差为4.26%，说明次声波的界面传播效应会影响定位精度，不同介质中的定位效果不如同一介质定位效果。

表3 不同介质模型中三测点定位坐标

在定位土壤中的次声源，而接收传感器位于空气中时，由于次声波在不同介质之间传播，其传播路线将在界面产生偏折，导致定位误差。由于折射角越大，定位误差越小，故应当将接收传感器尽量放置于距离界面垂直距离较大处。另外，由于本文的多测点振速矢量直线汇聚声源定位方法是一种数理统计优化算法，可有效的减少由于传播偏折产生的定位误差，表明该方法应用于工程快速定位具有很好的优势。