基于双参数地基系统的改进傅里叶级数振动方法研究

王 吉， 高芳清,2

(1. 西南交通大学 力学与工程学院，成都 610031；2. 西南交通大学 应用力学与结构安全四川省重点实验室，成都 610031)

弹性地基上矩形薄板作为一种常用的结构单元，广泛应用于工程建设中，如航天发射场坪、码头平台、高速公路刚性路面等。在弹性地基的研究中，双参数地基模型不仅改进了Winkler地基不连续的缺陷，在数学处理上也比弹性半空间模型简单，同时也能较好地模拟土体的力学性能[1]。因此，双参数地基模型受到了许多学者的广泛关注。

近年来，国内外学者对双参数地基上矩形板的振动问题进行了大量的研究[2-7]。Yang[8]基于Vlazov假定考虑了板外域地基沉降，利用有限元方法研究了双参数地基上四边自由矩形薄板的弯曲问题。竹学叶等[9]通过变分法导出了双参数地基上自由矩形薄板的边界条件，并用有限元方法对该问题进行了分析。Lam等[10]将格林函数应用到研究双参数地基上一组对边简支另一组对边任意的矩形薄板自由振动问题上，但理论建模中对含自由边界的情况未考虑板外域地基沉降的影响。Trong[11]利用有限差分法研究了不同边界条件下Winkler地基和双参数地基上矩形薄板的弯曲问题，并基于Vlazov假定研究了双参数地基上四边自由矩形板的弯曲问题。杨端生等[12]针对双参数地基上正交异性矩形薄板的稳定和振动问题给出了一般解析解，同样未考虑板外域地基沉降的影响。

目前，关于双参数地基上板结构的研究仅局限于三种经典边界条件的组合形式，且对不同的边界条件，需重新假设位移函数，求解过于复杂且缺乏统一性。同时，因边界条件的局限性，现有关于双参数地基上含自由边界或弹性边界矩形薄板振动问题的研究，忽略了板外域地基的沉降，而结构在该类边界上弯曲位移不为零，将导致基底压力向地基板外域传递和扩散，忽略其影响会产生较大的误差，且误差值对地基参数极为敏感。

因此，本文针对双参数地基上任意边界矩形薄板的弯曲振动问题进行研究，基于Kirchhoff薄板理论，采用改进Fourier级数方法[13-14]来描述弯曲位移函数，以严格满足任意边界上位移协变条件和力的平衡条件；通过竖向和扭转方向的弹性组件及其参数设定来模拟边界约束类别与状态；根据Vlazov假定[15]，分别将双参数地基板外域的沉降表示为板边、板角的位移和一个指数衰减函数的乘积；结合Hamilton原理，建立可统一解决双参数地基上任意边界矩形薄板弯曲振动问题的分析模型。通过参数化分析，并与文献结果和有限元计算结果进行对比，验证了本文方法具有较快的收敛速度和较高的计算精度；在此基础上，研究了不同自由边界数组合和弹性边界下地基沉降对振动特性的影响。

1 理论模型

1.1 Vlazov地基模型简介

对于单一薄压缩层和抗剪强度较低的软土质地基，单参数的Winkler地基模型较为适用，其采用相互独立且均匀分布的竖向弹簧单元模拟地基作用，并假设土介质表面任一点处的位移w与作用在该点的应力q成正比，而与作用在其他各点的应力无关，其表达式为

kw(x,y)=q(x,y)

(1)

式中，k为地基反力系数，也可称为基床系数。

对于密实厚土层或整体岩石土层的分析，Winkler地基模型忽略了土体间存在的相互剪切作用。为更好地模拟土体的连续性，双参数地基模型采用两个独立的弹性参数分别表示土体的抗压和剪切性能，且经适当的参数选取能够恰当地描述地基的力学性能。

双参数地基模型中Vlazov模型的两个地基参数物理意义明确，且理论体系严密，所以本文主要针对Vlazov地基模型进行简要介绍。

该模型从弹性力学空间问题的基本方程出发，对于平面尺寸为无限大，竖向为有限或无限深度的弹性层，假设其竖向位移沿竖向按某一设定的函数关系变化，其土体特征函数表示为

kw(x,y)-2t∇2w(x,y)=q(x,y)

(2)

式中，k和2t分别为地基的压缩基床系数和剪切基床系数。从式(1)和式(2)可看出，当剪切基床系数2t趋于零时，双参数地基模型将转化为Winkler地基模型。其中，k，2t与地基弹性模量Es，泊松比μs，地基深度H及地基竖向位移沿竖向的变化函数h(z)有关，可表示为

(3)

(4)

Vlazov和Leontiev提出了多种竖向变化函数，如按线性函数或指数函数变化

(5)

式中：γ为地基相关常数；L为结构某一特征尺寸。

目前，对于双参数地基中两参数的确定需要通过大量的实验方法得到，而本文重点针对双参数地基上任意边界矩形薄板的振动建模方法进行研究。因此，本文对双参数地基的压缩基床系数k和剪切基床系数2t的确定方法不做研究，在参数化分析中直接引用文献中的数值进行分析。

1.2 双参数地基上任意边界矩形薄板振动理论建模

双参数地基上的矩形薄板沿边界处采用均匀分布的竖向弹簧和扭转弹簧来模拟边界约束作用，如图1所示。通过改变弹性组件参数实现各类边界条件的设定，以x=0边界为例，如表1所示，表中边界条件通过设置约束弹簧刚度的指数系数ks进行模拟。

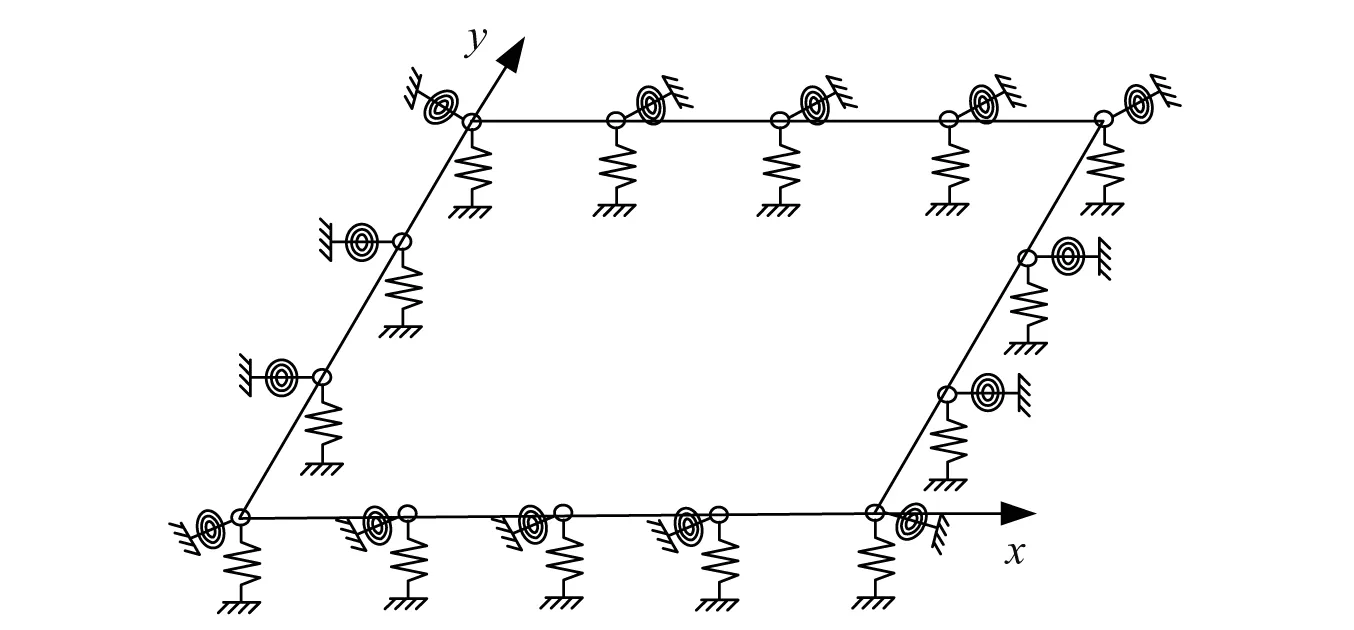
图1 矩形薄板弯曲振动模型

表1 弹性组件参数与边界条件关系

为得到双参数地基上矩形薄板的弯曲振动方程，采用Hamilton原理进行建模，其方程可表示为

(6)

式中：T为系统的总动能；V为系统的总势能。

系统的总势能V可表示为

V=Vbending+Vspring+Vfoundation,in+Vfoundation,out

(7)

式中：Vbending为其上矩形薄板的弯曲势能；Vspring为边界约束弹簧的弹性势能；Vfoundation,in为板内地基的变形势能；Vfoundation,out为板外域地基的变形势能。

基于Kirchhoff薄板理论，图1中矩形薄板的弯曲势能和边界约束弹簧的弹性势能可具体表示为

(8)

(9)

式中：kx0,kxa,Kx0,Kxa分别为x=0和x=a边界上的竖向弹簧刚度和扭转弹簧刚度；ky0,kyb,Ky0,Kyb分别为y=0和y=b边界上的竖向弹簧刚度和扭转弹簧刚度；D=Eh3/(12(1-μ2))为板的弯曲刚度。

双参数地基中，由于土体间存在相互剪切作用，会导致基底压力向周边传递和扩散。因此，除考虑板内地基的变形势能外，还需考虑板外域地基的变形势能。板内地基变形势能[16]为

(10)

针对板外域地基的变形势能，可将板外地基分为八个区域，如图2所示，图中区域Ω1，Ω2和Ω4的公共交点为坐标原点。

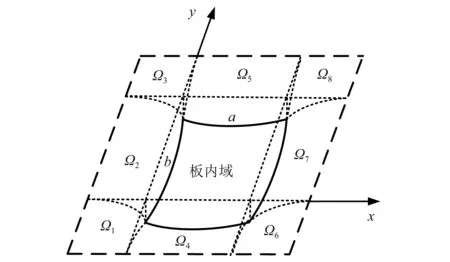
图2 双参数地基系统板外域地基沉降

根据Vlazov假定，分别将每个区域的沉降表示为板边、板角的位移和一个指数衰减函数的乘积，如表2所示。

表2 板外域位移函数表达式

板外域地基应变能为

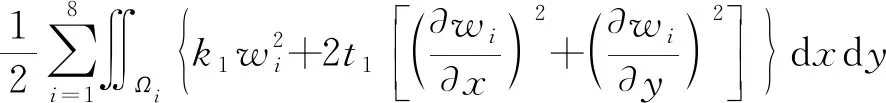
(11)

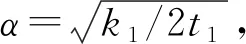
系统的总动能具体表达式为

(12)

式中：ω为角频率；ρ，h，μ分别为板的密度、厚度和泊松比。

1.3 弯曲位移函数的改进Fourier级数表达式

为模拟弹性边界条件，本文引入改进傅里叶级数方法，使弯曲位移函数能够严格满足任意边界条件，其表达式为

(13)

式中：λam=mπ/a；λbn=nπ/b； 与x相关的辅助函数ξia(x)可表示为

(14)

(15)

(16)

(17)

式(14)～式(17)需满足ξ′1a(0)=ξ′1a(a)=ξ‴1a(0)=ξ‴1a(a)=1，且其他一阶和三阶导数沿x=0和x=a边界都为零。相应地，辅助函数ξib(y)可将式(14)～式(17)中a和x分别替换为b和y。通过辅助函数的引入，可将弯曲位移函数在边界处关于x和y的一阶和三阶偏导潜在的不连续有效地转移到辅助项，从而改善级数的收敛性。

将弯曲位移函数(13)代入Hamilton方程式(6)中，并对未知的Fourier系数求极值，可以得到一个线性方程组，将其写成矩阵表达式为

(K-ω2M)A=0

(18)

式中：A为位移函数w(x,y)中二维Fourier级数和辅助级数的未知系数向量，其形式为

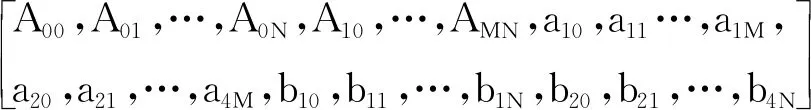
(19)

K，M分别为双参数地基上矩形薄板弯曲振动的刚度矩阵和质量矩阵，其形式分别为

(20)

(21)

为表述简洁，下列仅给出刚度矩阵K和质量矩阵M第1行第1列的子矩阵表达式，类似地，可表述出其他子矩阵表达式。表达式中，将引入新的符号来描述子矩阵中每一元素的位置，s=m(N+1)+n+1，l=m1(N+1)+n1+1，m=0,1,…,M，n=0,1,…,N，m1=0,1,…,M，n1=0,1,…,N，M，N表示展开级数的截断数。

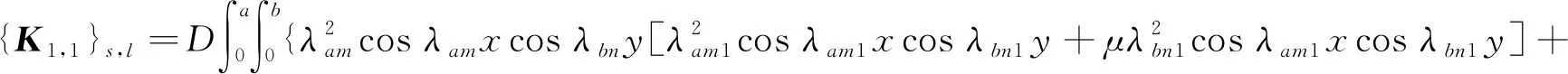
(22)

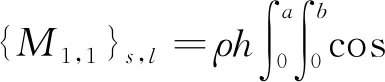
(23)

2 参数化分析

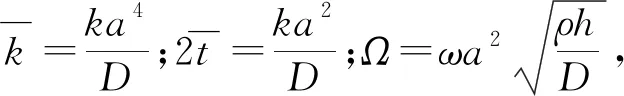
为检验本文方法的收敛性，通过求解矩阵表达式(18)，得到了双参数地基上矩形薄板在FFFF边界下截断数M和N取不同值时的无量纲固有频率，如表3所示。其中，FFFF表示边界x=0，x=a，y=0，y=b上均为自由。为评价收敛精度，表中同时给出了相对误差，表示当截断数取相邻的两整数时前六阶频率的最大相对误差(最大相对误差=max{[(Ωj)Z-(Ωj)Z+1]/(Ωj)Z+1×100%}，其中，(Ωj)Z表示截断数M=N=Z时，系统第j阶无量纲固有频率)。从表中可知，当M=N>3时，最大相对误差趋于零，求解结果趋于稳定。

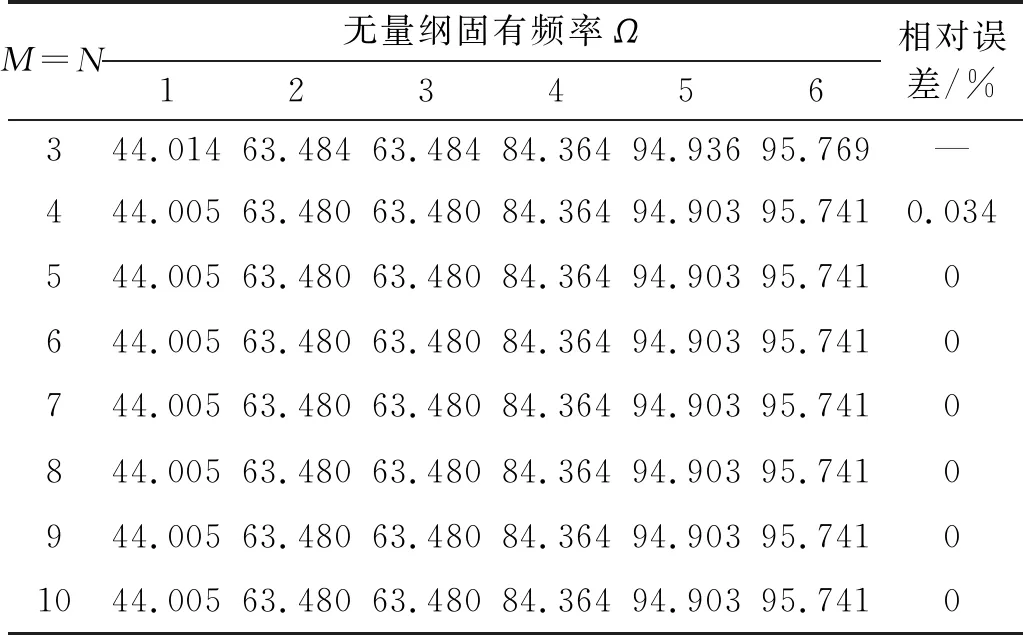
表3 双参数地基上FFFF矩形薄板在不同截断数下的无量纲固有频率

探究弹性约束边界和地基沉降对结构振动特性的影响(考虑板外域地基沉降时k=k1, 2t=2t1，不考虑板外域地基沉降时k≠k1=0, 2t≠2t1=0)，考虑竖向弹簧刚度系数kx0=kxa=ky0=kyb=D×10ks，扭转弹簧刚度系数均为零，绘制有无地基沉降下系统基频随竖向弹簧刚度系数的变化曲线，如图3所示，标记为“竖有/无沉降”；扭转弹簧刚度系数Kx0=Kxa=Ky0=Kyb=D×10ks，竖向弹簧刚度系数均为零，绘制有无地基沉降下系统基频随扭转弹簧刚度系数的变化曲线，如图3所示，标记为“扭有/无沉降”；竖向和扭转弹簧刚度系数一致性变化kx0=kxa=ky0=kyb=Kx0=Kxa=Ky0=Kyb=D×10ks，绘制有无地基沉降下系统基频随两类弹簧刚度系数的变化曲线，如图3所示，标记为“合有/无沉降”。

从图3中可知，约束弹簧刚度系数大于D×106(数值上≈5×1010)时，结构基频保持恒定，且板外域地基几乎不会产生沉降，以下分析中，可取该值模拟刚性约束；约束弹簧刚度系数小于D×104(≈5×108)时，不考虑板外域地基沉降对结果影响较大，且随约束弹簧刚度系数的减小而增加；相较扭转弹簧，板外域地基沉降产生的影响对竖向弹簧刚度系数的变化更为敏感。

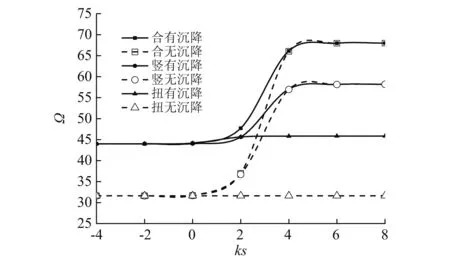
图3 边界约束弹簧刚度系数和地基沉降对系统基频的影响曲线

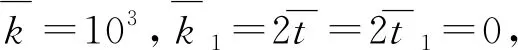
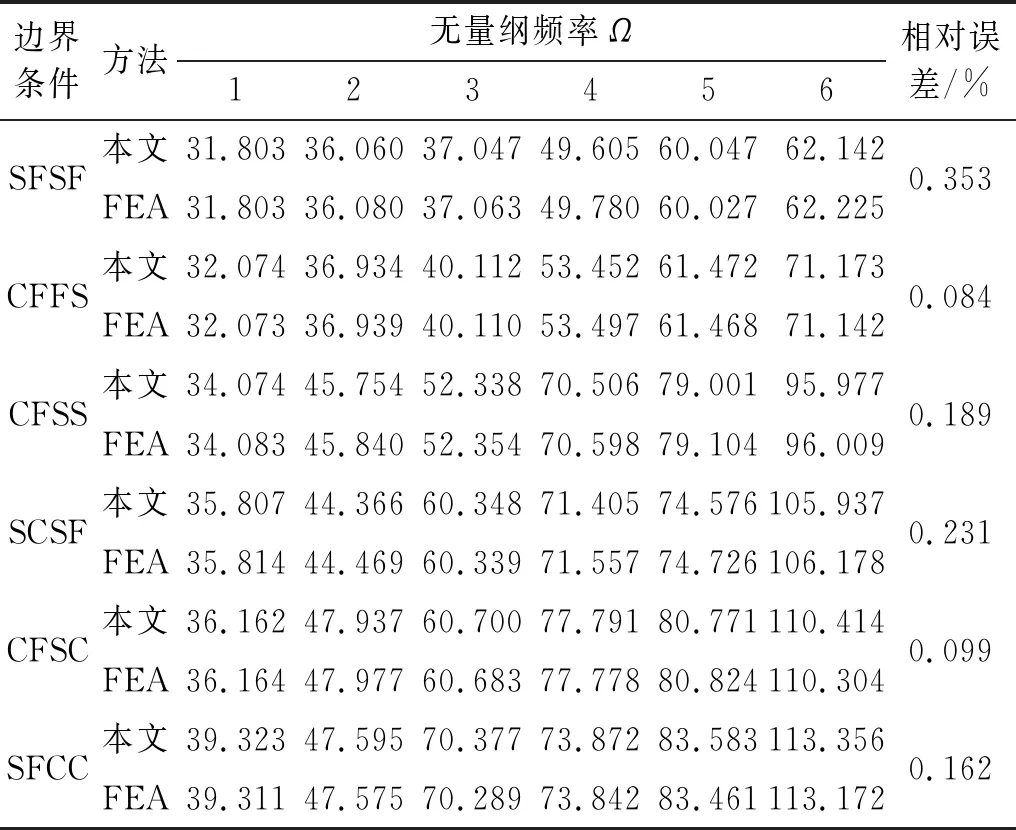
表4 Winkler地基上不同边界矩形薄板的无量纲固有频率

为进一步检验本文方法的准确性，分别给出双参数地基上SSSS,SCSC, SSSC, SSCF, SSSF, SFSF矩形薄板第一阶和第六阶无量纲频率，并将Lam等方法的结果与本文方法进行对比。需要特别说明的是，Lam等的建模方法中并未考虑板外域地基的沉降，即k≠k1=0, 2t≠2t1=0。综合表5和表6可知，最大相对误差为0.310%，两种结果吻合良好，进而验证了本文方法的准确性。

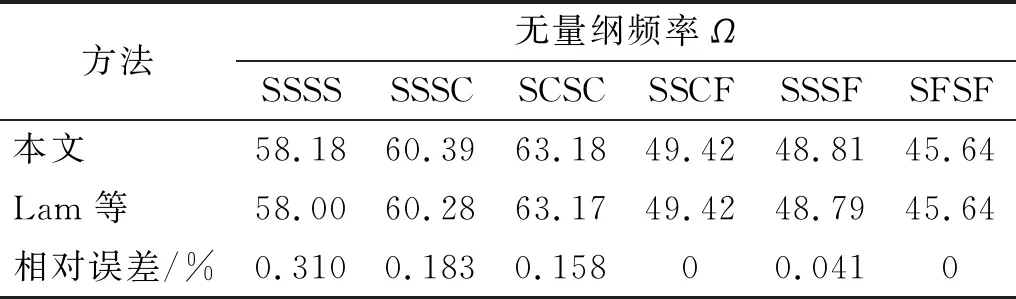
表5 双参数地基上矩形薄板在不同边界条件下的第一阶固有频率

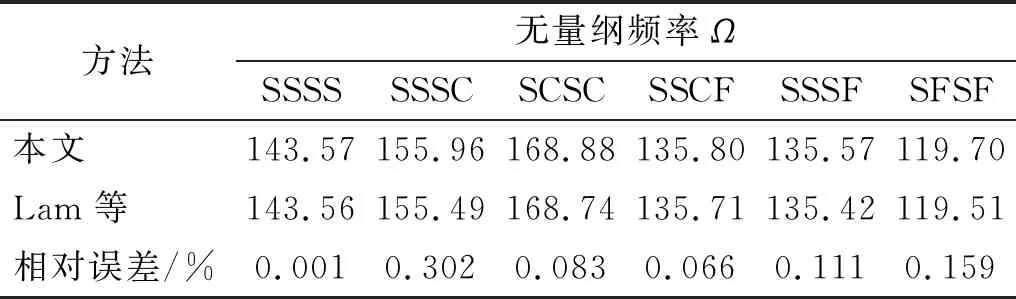
表6 双参数地基上矩形薄板在不同边界条件下的第六阶固有频率

基于以上研究，将进一步探究双参数地基系统在不同自由边界数组合下板外域地基沉降对固有频率的影响。通过数值求解，分别给出了考虑地基沉降和不考虑地基沉降情况下SSSF，SFSF，SSFF，SFFF，FFFF边界条件下系统的基频，如表7所示。表中，给出两种结果的相对偏差，以评价地基沉降的影响效果。

从表7中可知，FFFF边界的基频相对偏差最大，为28.15%。即，含自由边界数越多，相对偏差越大，地基沉降影响越大；自由边界数相同但位置分布不同的SFSF与SSFF结果相比，SSFF边界条件下偏差更大，这是因为SSFF边界下，不仅需要考虑自由边上的地基沉降，还需考虑两相邻自由边角点域的地基沉降。

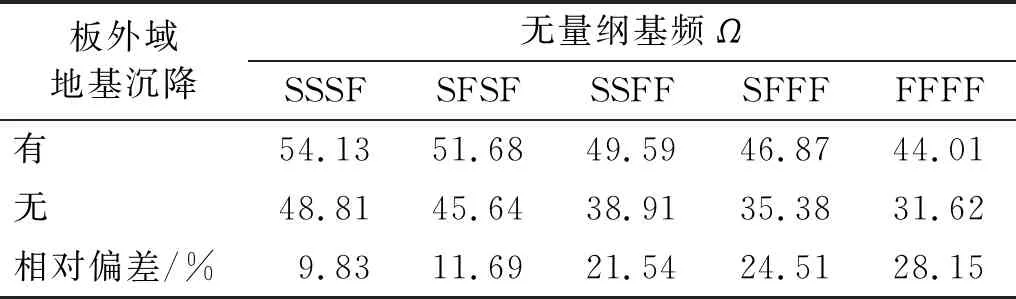
表7 双参数地基上不同自由边界数及位置分布的矩形薄板基频

3 结 论

(1) 本文针对双参数地基上矩形薄板的弯曲振动问题，基于改进Fourier级数方法和Vlazov假定，提出了一种使其能在任意边界条件下考虑板外域地基沉降的振动分析方法。通过数值算例，并与文献结果和有限元计算结果进行对比，验证了本方法具有较快的收敛速度(M=N>3时结果趋于稳定)和较高的计算精度(误差小于0.353%)。

(2) 不考虑板外域地基沉降对结构振动频率影响较大，且随约束弹簧刚度系数的减小而增加；当约束弹簧刚度系数大于D×1010(数值上≈5×1010)时，板外域地基几乎不再产生沉降；相较扭转弹簧，板外域地基沉降产生的影响对竖向弹簧刚度系数的变化更为敏感。

(3) 通过参数化分析，本模型可适用于Winkler地基上任意边界矩形薄板振动问题的研究，拓展了本模型的适用范围。

(4) 探究不同自由边界数组合下板外域地基沉降对固有频率的影响发现，仅含一条自由边界时，不考虑板外域地基沉降产生的误差为9.83%，且误差值随自由边界数的增加而增加；自由边界数相同但位置分布不同时，含相邻自由边界产生的误差更大。