含级间相对浮动的两级行星传动系统均载特性研究
2021-07-22陆崇山王晓笋冷晓鲁巫世晶
陆崇山, 王晓笋, 冷晓鲁, 巫世晶
(武汉大学 动力与机械学院,武汉 430072)
行星齿轮传动具有结构紧凑、传动比大、承载能力强等优点,其载荷由多个行星轮共同承担,有效减小了齿轮啮合力,增加了齿轮寿命,广泛应用于电力、航空、船舶等行业。在实际应用中,由于制造安装误差,配合间隙等因素的影响,各行星轮的受力并非完全相同,载荷无法实现理想化的均匀分流,容易产生冲击和噪声,影响系统的承载能力。多级行星齿轮传动系统相比单级系统结构更加复杂,影响因素更多,更容易因载荷分配不均而影响正常使用。
目前,国内外不少研究者对行星齿轮传动的动力学建模和均载特性进行了相关研究。Kahraman[1-2]采用集总参数法建立了单级行星齿轮的动力学模型,考虑了制造和安装误差,提出动态均载系数用以衡量行星轮系的均载特性;Singh[3]采用一种系统级的建模方法,分析了制造误差和轴承支撑刚度对行星轮系载荷分配的影响;周璐等[4-6]建立了考虑多种非线性因素的2K-H行星轮系“平移-扭转”耦合动力学模型,并分析了误差和中心构件浮动对系统均载特性的影响。以多级行星齿轮传动系统为研究对象,肖正明等[7]建立了三级减速器行星齿轮系统纯扭转动力学模型,求解了系统的动态响应;刘辉等[8]建立了两级行星齿轮传动系统“平移-扭转”耦合动力学模型,研究了两级行星减速系统在不同载荷下的啮合力频率耦合现象和均载特性;Sheng等[9-10]分析了两级行星齿轮传动系统的静态和动态均载系数以及中心齿轮的运动轨迹规律,并进行了实验验证。
以上关于多级行星传动系统的研究中均没有考虑级间连接构件的相对浮动。本文考虑了时变啮合刚度、啮合误差、齿侧间隙等非线性内部激励,首次在动力学模型中引入级间相对浮动,建立了两级行星齿轮传动系统“平移-扭转”耦合动力学模型,对系统的均载特性进行了分析,为进一步研究多级行星轮系动力学特性提供了理论基础,对多级行星轮系的优化设计具有一定参考意义。
1 系统动力学模型
1.1 模型分析
本文以风电机等设备使用较多的两级增速行星齿轮传动系统为研究对象[11],系统结构简图如图1所示,由两级2K-H行星轮系串联组成,输入端为第一级行星架c1,输出端为第二级太阳轮s2,两级内齿圈r1,r2固定在齿轮箱外壳上,第一级的太阳轮s1与第二级的行星架c2之间存在相对浮动间隙Δbr,pn,qn(n=1,…,N,N为行星轮个数)分别表示第一级和第二级行星轮。

图1 两级行星传动系统简图
采用集总参数法建立系统动力学模型[12-13],将齿轮的啮合等效为弹簧阻尼系统。因串联的两级轮系结构相同,仅以第一级为例,其“平移-扭转”耦合动力学模型如图2所示。图中下标s1,c1,r1,pn分别为太阳轮、行星架、内齿圈和行星轮,定坐标系OXY和行星架随动坐标系Oxy均以太阳轮理论回转中心为原点,Oxy以行星架的理论角速度ωc1相对于OXY旋转。图中各构件拥有3个自由度,xi,yi(i=s1,c1,r1,pn)为构件在x,y方向的平移位移,θi为构件的扭转角度。mi,Ii分别为各构件的质量和转动惯量;ri为分度圆半径,其中rc=rs+rp;ki,kit分别为各构件的平移支承刚度和扭转刚度;kj,2bj,cj,ej(j=s1pn,r1pn)分别为各啮合副的啮合刚度、齿侧间隙、啮合阻尼和综合啮合误差。
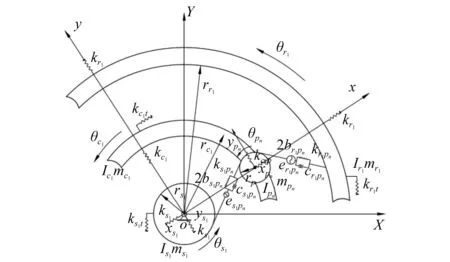
图2 “平移-扭转”耦合动力学模型
1.2 非线性参数描述
1.2.1 时变啮合刚度
齿轮副啮合时,处于啮合接触的轮齿对数在1和2之间交替变化。将一对轮齿的啮合简化为1个弹簧,两对轮齿啮合则为两根相同的弹簧并联,啮合刚度用弹簧刚度来表示,随着啮合轮齿对数的变化呈周期变化,近似为周期矩形波的形态。将时变啮合刚度简化为平均刚度值和波动量的叠加,刚度波动量用三角函数表示,以第一级轮系为例,其时变啮合刚度可表示为
(1)
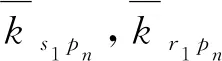
1.2.2 综合啮合误差
在齿轮传动系统安装时,实际安装中心与理论安装中心不一致会导致构件存在安装误差;齿轮的实际回转中心与理论回转中心不一致会产生偏心误差。将啮合副构件的各类误差表达成啮合线上的等效位移并进行叠加,以综合啮合误差表示。以第一级为例,两对啮合副综合啮合误差的表达式为
es1pn=As1·sin[-ωc1·t+αs1+βs1-ψpn]-
Apn·sin(αpn+βpn)+
Es1·sin[(ωs1-ωc1)·t+αs1+γs1-ψpn]-
Epn·sin[(ωpn-ωc1)·t+αs1+γpn],
er1pn=Ar1·sin[ωc1·t+αr1-βr1+ψpn]+
Apn·sin(αr1-βpn)+
Epn·sin[-(ωpn-ωc1)·t+αr1-γpn]+
Er1·sin[ωc1·t+αr1-γr1+ψpn]
(2)
式中:Ai,Ei(i=s1,r1,c1,pn)分别为各构件的安装误差和偏心误差的幅值;βi,γi分别为安装误差和偏心误差的初始相位;αi为压力角;ψpn=2π(n-1)/N为第n个行星轮的位置角;ωi为构件角速度。
1.2.3 齿侧间隙
由于制造和安装过程中难以避免的偏差以及长期运转后的磨损等因素,轮齿啮合对之间存在齿侧间隙,导致啮合副产生冲击。以第一级为例,存在齿侧间隙时啮合力和啮合刚度的关系可以用1个分段非线性函数f(δj)(j=s1pn,r1pn)描述
(3)
式中:bj为齿侧间隙的一半;δj为啮合副的相对啮合位移,表示齿轮的振动位移在啮合线上的投影之和。定义振动位移使啮合线压缩为正方向,各啮合副相对啮合位移表达式为
δs1pn=(xpn-xs1)·sin(φs1pn)+(ys1-ypn)·
cos(φs1pn)+us1+upn-uc1·cos(αc1)-es1pn,
δr1pn=(xpn-xr1)·sin(φr1pn)+(yr1-ypn)·
cos(φr1pn)+ur1-upn-uc1·cos(αc1)-er1pn,
δpnc1x=xpn-xc1,
δpnc1y=ypn-yc1
(4)
式中:φs1pn和φr1pn为两种啮合副的位置方向角;ui=θi·rbi(i=s1,r1,c1,pn)为各构件的线位移,rbi为构件的基圆半径。
1.2.4 级间相对浮动间隙
在两级行星轮系中,第一级输出太阳轮可以通过花键轴与第二级输入行星架连接。采用间隙配合的花键连接在径向可以给予两构件一定的相对浮动间隙Δbr,在运转时两构件产生不同的径向位移。相对浮动间隙的存在会影响太阳轮的径向支承刚度,引入刚度变化系数μ
(5)
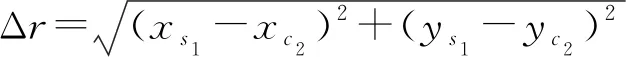
(6)
2 动力学微分方程
系统中各构件有3个自由度,第一级输出太阳轮和第二级输入行星架通过中间轴相连,视为1个整体用a表示,有1个扭转位移,因此当存在相对浮动间隙时共有5个自由度xs1,ys1,xc2,yc2,θa。各级行星轮个数设为3,则整个系统有35个自由度。利用第二类拉格朗日方程,并引入上述非线性参数,得到系统无量纲动力学微分方程组为
(7)
(8)
(9)
(10)
(11)
(12)
(13)
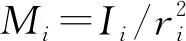
3 均载特性分析
3.1 均载系数计算
用均载系数衡量一组行星轮在啮合中载荷不均匀的程度。以第一级为例,轮系在1个啮合周期内的均载系数为
(14)
式中:Fs1pn,Fr1pn分别为s1p,r1p啮合副的啮合力,可以通过数值方法求解微分方程组得到。此处啮合周期Tm1=2πωd/ωm1,表示在随动坐标系Oxy中一对轮齿的无量纲啮合时间,与无量纲处理后的啮合频率相对应。啮合副在一段时间内的均载系数用期间所有啮合周期均载系数的最大值表示
Bs1pn=|bs1pn-1|max+1Br1pn=|br1pn-1|max+1
(15)
由式(15)可以看出,均载系数值越大,各行星轮载荷分配越不均匀,均载性能越差;值越接近1,均载性能越好。由于行星轮在两对啮合副的啮合力作用下保持平衡,可知啮合副s1pn和r1pn的啮合力和均载系数大小相等,因此本文仅对太阳轮—行星轮啮合副的均载系数进行分析。系统各构件基本参数如表1所示,第一级和第二级相同构件相应参数相同。给予系统输入扭矩5 000 N·m,负载扭矩500 N·m,输入转速200 r/min。

表1 传动系统基本参数
3.2 无级间相对浮动时误差耦合对均载特性的影响
当不考虑级间相对浮动间隙,即当Δbr=0时,分别分析单一构件和多构件多种误差耦合对系统均载特性的影响。
3.2.1 单一构件误差耦合对均载特性的影响
由第二节分析可知,构件主要存在安装误差和偏心误差两种误差激励。以第一级太阳轮为例,分别计算太阳轮安装误差单独作用,设幅值20 μm,即当As1=20 μm,Es1=0,以及偏心误差单独作用,即当Es1=20 μm,As1=0下的均载系数,每对啮合副取200个啮合周期,得到各级的均载系数曲线如图3所示。由图3可知,当第一级太阳轮安装误差单独作用时,系统第一级均载系数为1.139 8,第二级均载系数为1.080 9;当偏心误差单独作用时,系统第一级均载系数为1.138 7,第二级均载系数为1.079 4。两种误差单独作用时,同一级的均载系数相差很小,表明安装误差与偏心误差单独作用时对系统均载特性的影响效果较为接近。两种情况下第一级轮系的均载系数均大于第二级,曲线波动幅度更大。
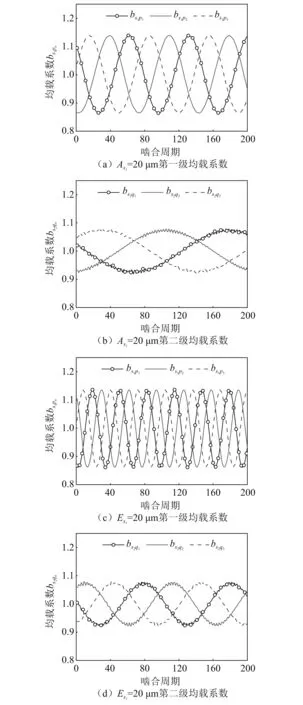
图3 单误差作用下系统的均载系数曲线
而计算第二级太阳轮安装误差单独作用,即当As2=20 μm,Es2=0时两级均载系数分别为1.025 1,1.432 3;偏心误差单独作用,即当Es2=20 μm,As2=0时两级均载系数分别为1.026 8,1.427 6,此时第二级均载系数均大于第一级,由此可以看出构件的误差主要影响所在一级的均载特性,对另一级影响程度相对较小。
当第一级太阳轮安装误差与偏心误差同时作用,即当As1=20 μm,Es1=20 μm时,系统的均载系数曲线如图4所示。由图4可知,当第一级太阳轮安装误差与偏心误差同时作用时,系统第一级均载系数为1.268 2,第二级均载系数为1.154 8,各级均载系数相比单误差作用时均变大,系统均载性能变差。此时系统均载系数曲线并未表现出周期性变化,对计算得到第一级s1p1啮合副的动态啮合力进行频谱分析,滤去低幅高频成分,结果如图5所示,图中坐标值均为无量纲处理后的结果。由图5可知,啮合力的频谱中除去直流成分外在0.013 5和0.031 5两个频率点出现峰值。由式(2)可知第一级太阳轮安装误差与偏心误差的激励频率分别为-ωc1和ωs1-ωc1,经无量纲处理后的值分别与频谱图中的两个峰值频率点相对应,说明系统此时均载特性的波动正是由两种误差激励共同引起的。由于两种误差激励的频率之比不是有理数,因此叠加后的均载系数曲线未表现出周期性变化。
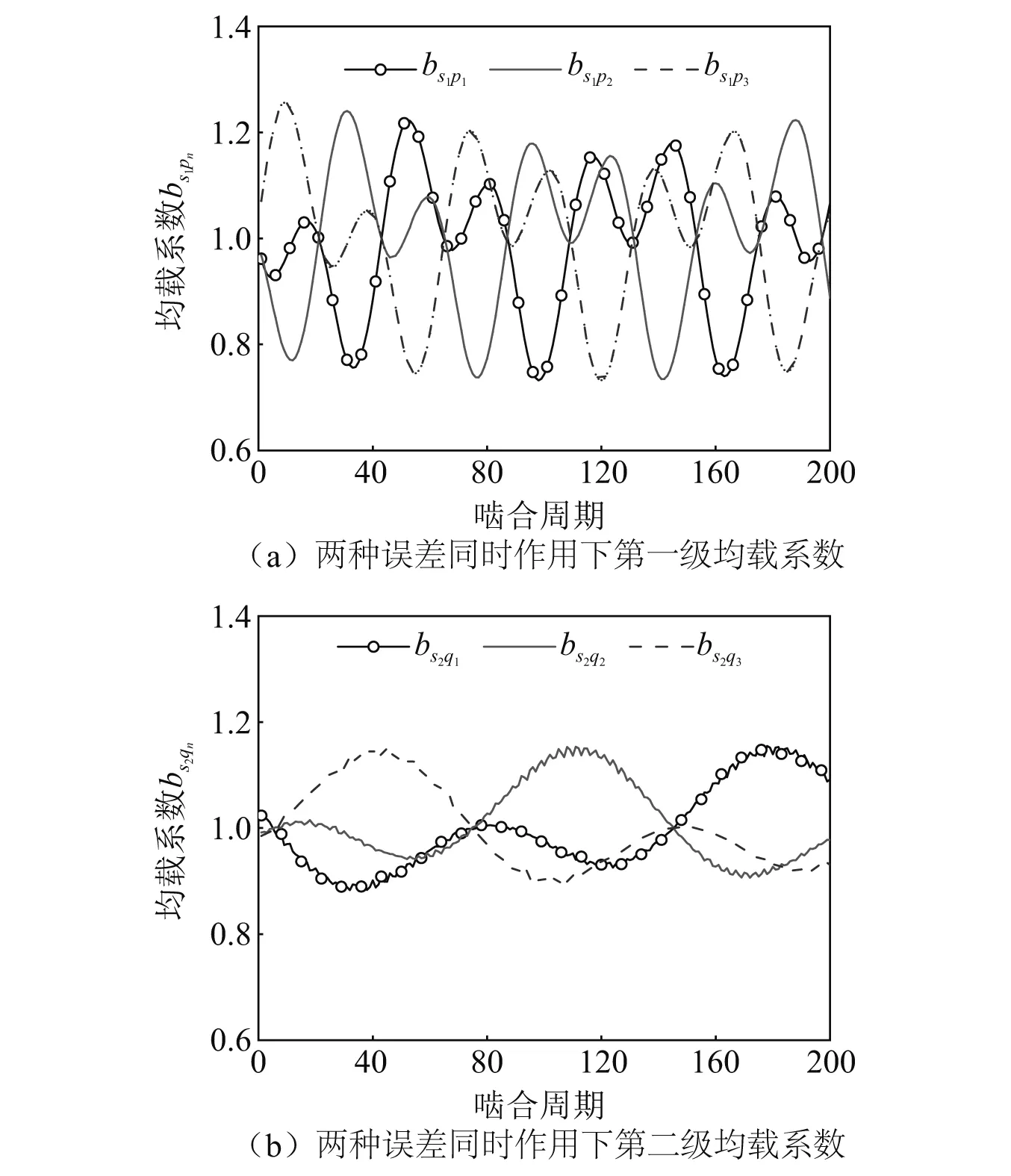
图4 两种误差同时作用下系统均载系数曲线
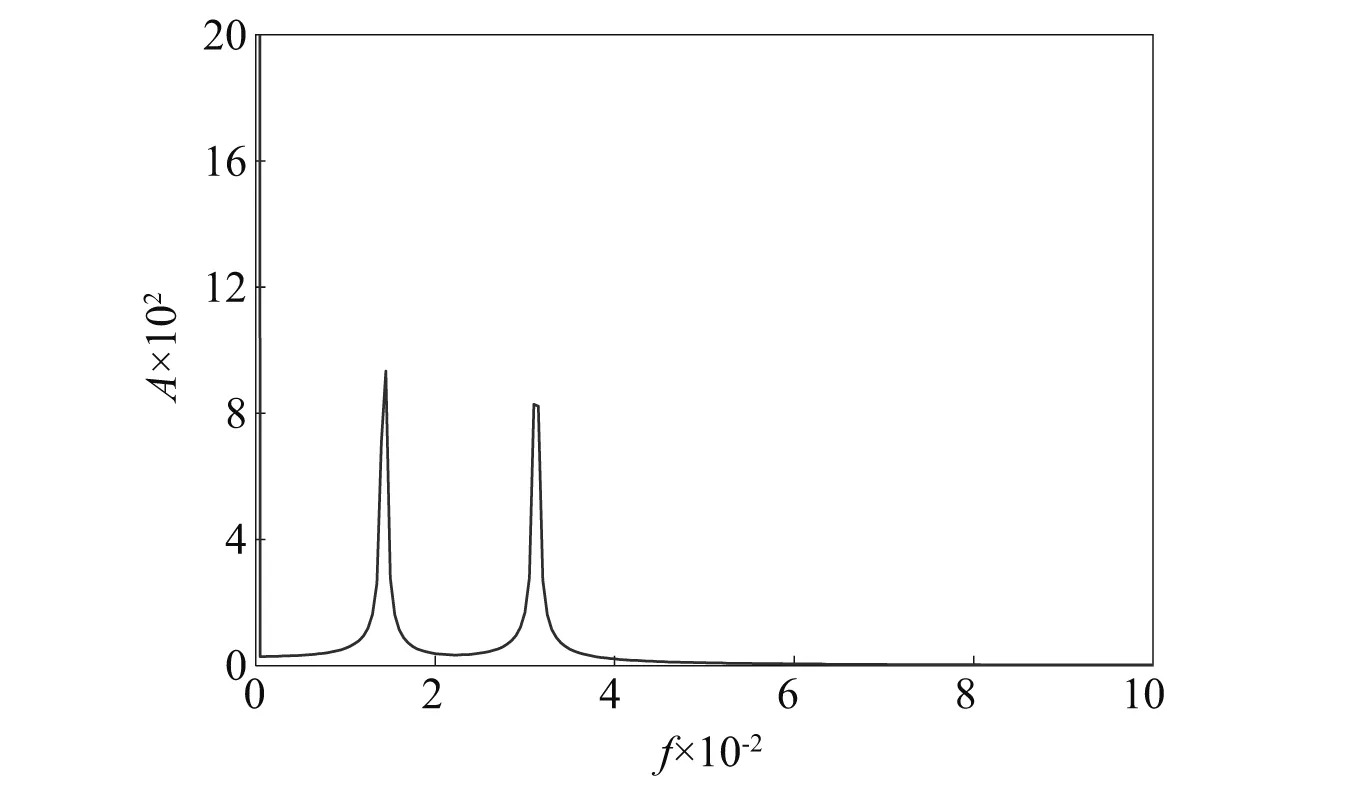
图5 两种误差作用下s1p1动态啮合力频谱图
3.2.2 多构件误差耦合对均载系数的影响
以第一级和第二级的太阳轮为例,当两级太阳轮的安装误差和偏心误差同时作用,且幅值相同,即As1=20 μm,Es1=20 μm,As2=20 μm,Es2=20 μm时,计算得系统的均载系数曲线如图6所示。由图6可知,当两级太阳轮两种误差同时作用时,系统第一级均载系数为1.301 9,第二级均载系数为1.893 3,均载系数相比单一构件误差作用时较大,且曲线波动更为无序。在相同误差幅值作用下,第二级的均载系数明显大于第一级,这是由于在系统运转时第二级行星轮承受的载荷更小,符合行星轮系载荷越小均载性能越差的理论结果[14]。
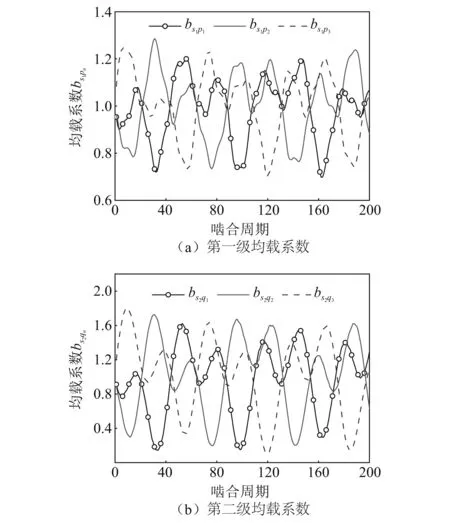
图6 多构件误差耦合时系统均载系数曲线
3.3 级间相对浮动对均载特性的影响
3.3.1 存在级间浮动时误差耦合对均载特性的影响
当级间相对浮动间隙Δbr=10 μm时,在第一级太阳轮安装误差与偏心误差同时作用下,即As1=20 μm,Es1=20 μm时,系统的均载系数曲线如图7所示。对比图4与图7可知,当存在级间相对浮动间隙时,在相同误差幅值作用下系统两级均载系数均更小,第二级达到了均载状态,说明级间相对浮动间隙能够有效改善系统的均载性能。改变第一级太阳轮两种误差的幅值,即当As1,Es1依次为20 μm,25 μm,30 μm,35 μm,40 μm时,计算得第一级均载系数依次为1.195 4,1.260 1,1.324 8,1.389 0,1.452 8,第二级均载系数为1.004 4,始终处于均载状态。同样,当第二级太阳轮两种误差以不同幅值作用,即当As2,Es2依次为20 μm,25 μm,30 μm,35 μm,40 μm时,第一级均载系数为1.000 3,第二级均载系数依次为1.803 2,1.962 8,2.110 1,2.262 8,2.413 8,第一级同样始终处于均载状态。与无级间相对浮动时的计算结果对比可知,级间相对浮动会明显减弱构件误差对另一级均载系特性的影响,改善整个系统的均载特性。
当两级太阳轮的误差共同作用,即当As1=20 μm,Es1=20 μm,As2=20 μm,Es2=20 μm,相对浮动间隙为10 μm时,系统的均载系数曲线如图8所示。由图8可知,此时系统第一级均载系数为1.218 5,第二级均载系数为1.803 4,对比图6可知存在级间相对浮动时系统两级均载系数都变小,系统均载性能得到改善。
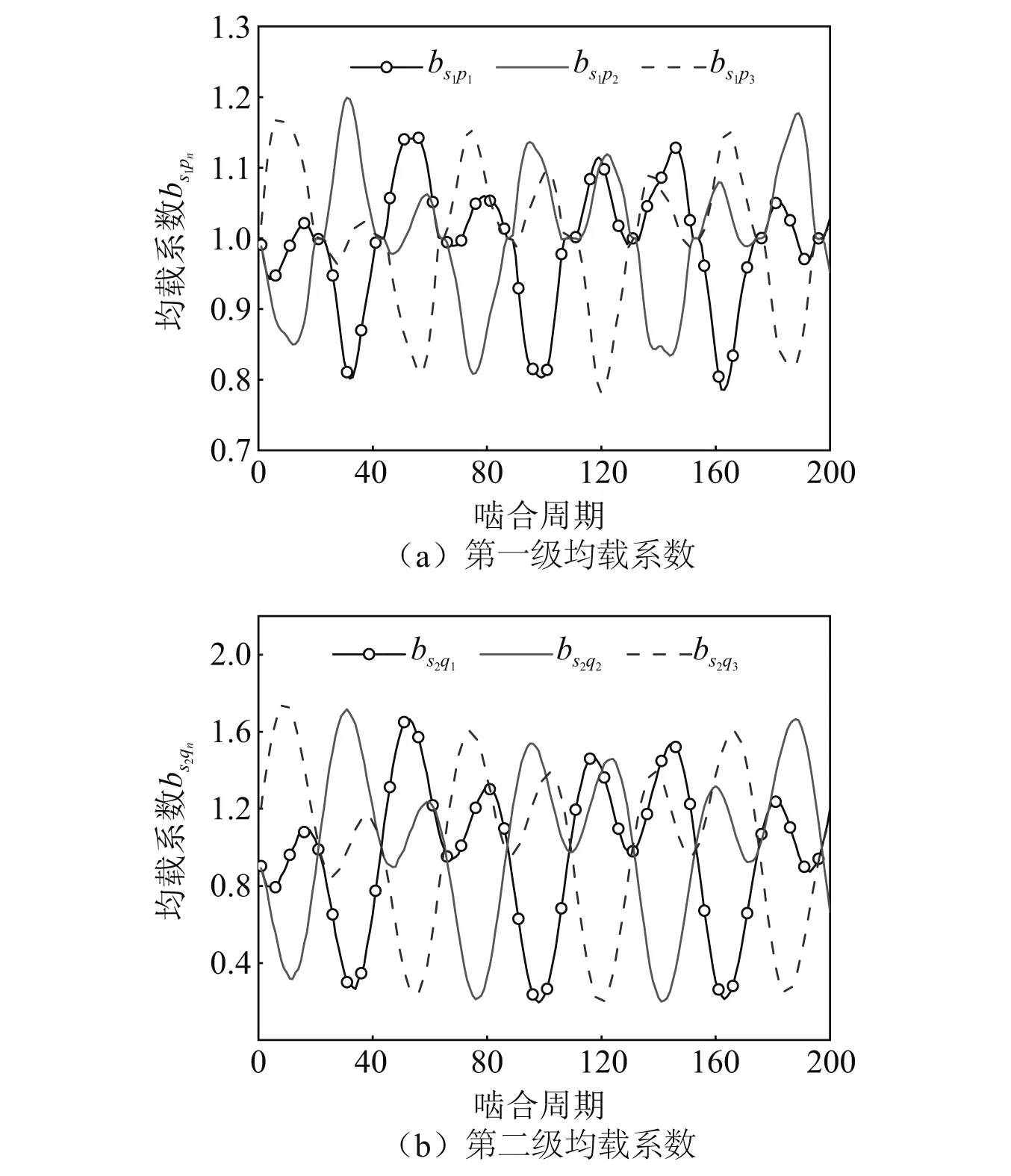
图8 存在级间浮动间隙时系统均载系数曲线
3.3.2 级间相对浮动间隙大小对均载特性的影响
当两级太阳轮误差同时作用,幅值均为20 μm,改变级间相对浮动间隙的大小,得到系统两级均载系数的变化趋势如图9所示。由图9可知,增大级间相对浮动间隙能够有效降低第一级的均载系数,当增大到一定值后第一级可以达到均载状态。但是间隙增大对第二级的均载系数影响很小。
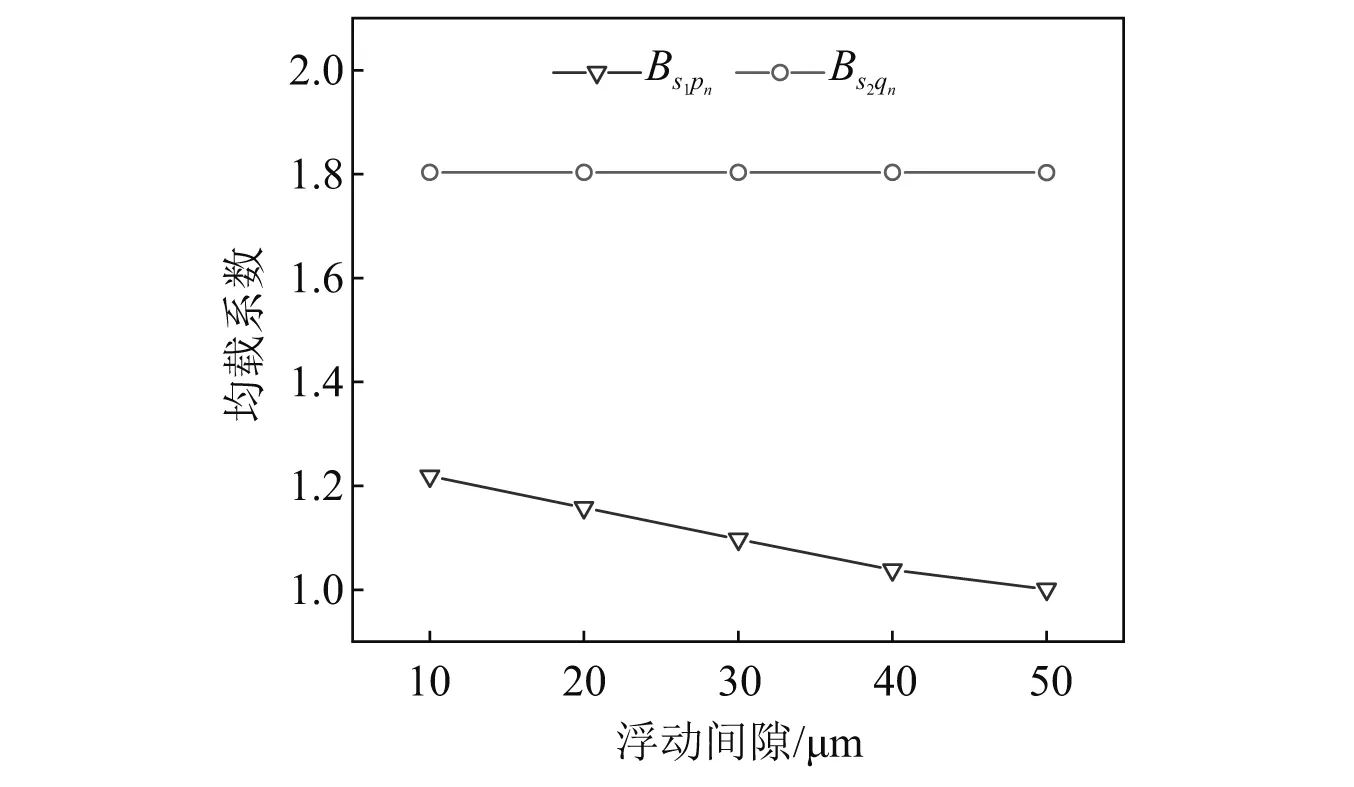
图9 不同浮动间隙时系统均载系数
4 结 论
采用集总参数法,建立了考虑级间相对浮动的两级增速行星齿轮传动系统“平移-扭转”耦合动力学模型,分别分析了有无级间相对浮动时构件多误差耦合以及级间相对浮动间隙的大小对系统均载特性的影响规律,得到了以下结论:
(1) 在无级间相对浮动的情况下,单一构件的多种误差共同作用会使系统均载性能变差,构件的误差对所在一级的均载特性的影响程度更大。
(2) 当两级多构件误差同时作用时,载荷相对较小的第二级级均载性能较差,因此在传动系统制造安装过程中应当着力提高第二级构件的精度等级。
(3) 在相同误差作用下,级间相对浮动能够有效改善系统的均载性能,且会明显减弱构件误差对另一级均载特性的影响。
(4) 增大级间相对浮动间隙能够有效改善第一级轮系的均载性能,而对第二级均载特性的影响很小。
