管道不可压缩流动压力脉动(伪声)的数值研究
2021-07-22蔡建程谢新俊MOCHALINIevgenBRAZHENKOVolodymyr鄂世举
蔡建程, 谢新俊, MOCHALIN Ievgen, BRAZHENKO Volodymyr, 鄂世举
(1. 浙江师范大学 工学院,浙江 金华 321004;2. 浙江省城市轨道交通智能运维技术与装备重点实验室,浙江 金华 321005)
管道系统出现在众多工程应用中,管道振动噪声造成管道系统的安全隐患,广受人们关注。引发管道振动的一个因素是主机动平衡差以及基础设计不当,而实际生产情况表明,引发管道振动另一个主要因素是流体压力脉动[1]。由于间歇加压,管道内压力在平均值上下脉动,而在管道弯曲部位,压力脉动会产生相应的随时间变化的激振力,引发振动与噪声。
在经典流体力学中,学者们在直管及弯头的水力损失方面进行了广泛的研究。对于弯管,弯头处存在二次流、射流-尾迹等现象的研究,具有较高的学术研究价值。近年来,管道气流脉动研究越来越热,主要集中在基于管道声学的传递矩阵法和基于计算流体动力学(computational fluid dynamics,CFD)的数值研究。
在管道声学压力的传递矩阵法研究方面,贺尚红等[2]利用传递矩阵法建立液压管网压力-流量传递函数模型,研究液压系统受泵源周期性吸排油机制影响产生流量脉动,流量脉动遇到系统负载阻抗后形成压力脉动。Cyklis等[3-4]也进行了类似的工作,用以研究压缩机管道系统气流脉动。声学传递矩阵法的优点是计算量小,通过把长管道系统分解成四端参数声学模型,进行快速预测。但当压力脉动幅度超过8%时,传递矩阵法将产生较大误差[5],所以有必要进行管道内压力脉动的CFD数值研究。
CFD方法能更为详细地得到管道内流场,特别是在弯管流动方面。对于弯管流动,弯头转弯半径和管道直径之比Rc/D是重要的无量纲参数。Tanaka等[6]利用大涡模拟(large eddy simulation,LES)结合壁面函数求解Rc/D=2的弯管流动,分析弯头处的非定常流动。Tan等[7]基于特征线分离算法的大涡模拟,计算了Rc/D=1和Rc/D=2两种情况的弯管流动,结果显示弯头曲率对于弯头横截面上的压力、速度以及二次流分布有很大影响。Dutta等[8]则用k-ε湍流模型求解Rc/D=2的弯管流动,研究分离点、再附点随雷诺数Re的变化情况。陈敏等[9]利用FLUENT软件的RNGk-ε湍流模型计算了不同雷诺数下90°弯管内的二次流。李静等[10]也利用相同方法数值研究了雷诺数和半径比Rc/D对90°弯管流动的局部阻力的影响。魏志等[11]利用LES方法对阀体后90°弯管内部流场进行了三维数值模拟,获得了蝶阀在全开状态下弯管内不同截面的流场特性和不同径向截面的涡旋结构,并与粒子图像测速试验结果进行了对比。梁开洪等[12]则研究了入流角对90°圆弧弯管流内的二次流、分离、偏流及流动阻力的影响。
在管道压力脉动研究方面,韩文龙等[13]利用ANSYS FLUENT软件建立了管道系统流动的CFD模型,提出了合理的边界条件,分析了往复式压缩机管道系统气流脉动的数值,并与试验比较,表明标准k-ε湍流模型在计算管道系统气流脉动时最为准确。马斓擎[14]利用ANSYS CFX软件模拟了进口质量流量脉动时弯管和阀门下游的压力脉动特性。
学者们利用CFD模拟管内流动时经常使用不可压缩流动假设,这是因为依据流体力学理论,对于Ma<0.3的流动通常看成不可压缩(流体密度ρ为常数)。对于不可压缩流动,水动力压力脉动为声学理论的伪声,管内水动力压力脉动特性的研究较少。本文先理论分析不可压缩流场压力脉动(伪声)与声波方程的区别,再利用CFD数值研究直管与弯管入口处设置简谐水动力压力脉动条件下,管内非定常流动的特性。
1 管道流动的数学模型
1.1 不可压缩流动数学模型
不可压缩流动Navier-Stokes方程
∇·v=0
(1)

(2)
式中,v,ρ,p,μ为流体速度、密度、压力及动力黏度。该连续方程和动量方程可以组成封闭的方程组,与相应的边界条件构成数学上的适定问题,而不需要求解能量方程。不可压缩流动压力p没有以与时间相关的形式出现,这归因于连续方程的非发展特点。
式(1)对时间求偏导后减去式(2)的散度,得到
∇2p=-ρ∇·[(v·∇)v]
(3)
可见,给定速度场时其压力场的控制方程为Poisson方程,压力与速度以椭圆型方程耦合。压力场的Poisson方程意味着扰动的传播速度为无穷大,即整个压力场同步变化,不同位置点扰动无时间差。对于一维模型,式(3)简化为
(4)
式中,u为x方向的流体速度。
1.2 一维管内可压缩流动模型(小扰动传播)
此处推导管内可压缩压力脉动的波动方程。一维的连续方程和动量方程分别为
(5)
(6)
根据Stokes假设有
λ=-2μ/3
(7)
假设波动为等熵过程,有
(8)
式中:κ为绝热指数;c为声速。连续方程式(5)转化为
(9)
对于管道里流动,把物理量分解成平均量和脉动量之和φ=φ0+φ′,认为脉动量与平均量相比是小量φ′≪φ0,把脉动量及其对自变量x,t的导数视为一阶微小量。式(6)对x求导,并且忽略流体黏性,得到
(10)
式(9)按φ=φ0+φ′变成
(11)
然后分别对x和t求导,得到
(12)
(13)
将式(12)、式(13)代入式(10),得到
(14)
考虑到u0相比于声速c很小,忽略u0项,得到经典声波方程
(15)
其行波解形式为f(x-ct),由于不考虑黏性,声压不随时间和距离衰减。周红等[15]把黏性力项(式(6)右端第二项)进行简化建模:把速度u的二阶导数项简化为阻尼系数α和速度u相乘,并且用分离变量法得到解析解,其中包括随时间衰减项exp(-αt/2ρ0)。
式(15)的行波解f(x-ct)表明扰动传播速度为c,当c→∞扰动对时间的求导项可以忽略,此时变成不可压缩流动的压力脉动情况。
2 管道不可压缩流动的数值计算
2.1 CFD模型
本文以管道内压力脉动为研究对象,分析其不可压缩流动的压力脉动特性。流体介质为不可压缩空气,密度为1.225 kg/m3,动力黏度为1.789 4×10-5Pa·s。所研究的直管直径D=0.190 m、长度为7.0 m。弯管由转弯半径为Rc=0.11 m的90°弯头连接两根直径D=0.190 m、长度为3.5 m直管构成,Rc/D=0.579。
直管和弯管的示意图,如图1所示。对于直管,沿管道中心线以及上部表面附近(离壁面0.2 mm处的边界层内),以2.0 m为间距设置流场计算的压力及速度监测点,从进口侧开始编号1~34(进出口处因为设置边界条件,所以不设置监测点)。弯管的前后两段直管内也类似地设置监测点,编号与直管一致,另外在弯头中心线以及上侧、内侧、外侧表面附近的边线上各设置7个监测点,参见图1(c)的局部放大图,以研究弯头处的流场脉动。对于弯管设置流向中间剖面和纵向中截面,用于分析内部流动。对于直管,管内流动基本上呈轴对称,所以仅设置流向中间剖面,参见图1(d)。
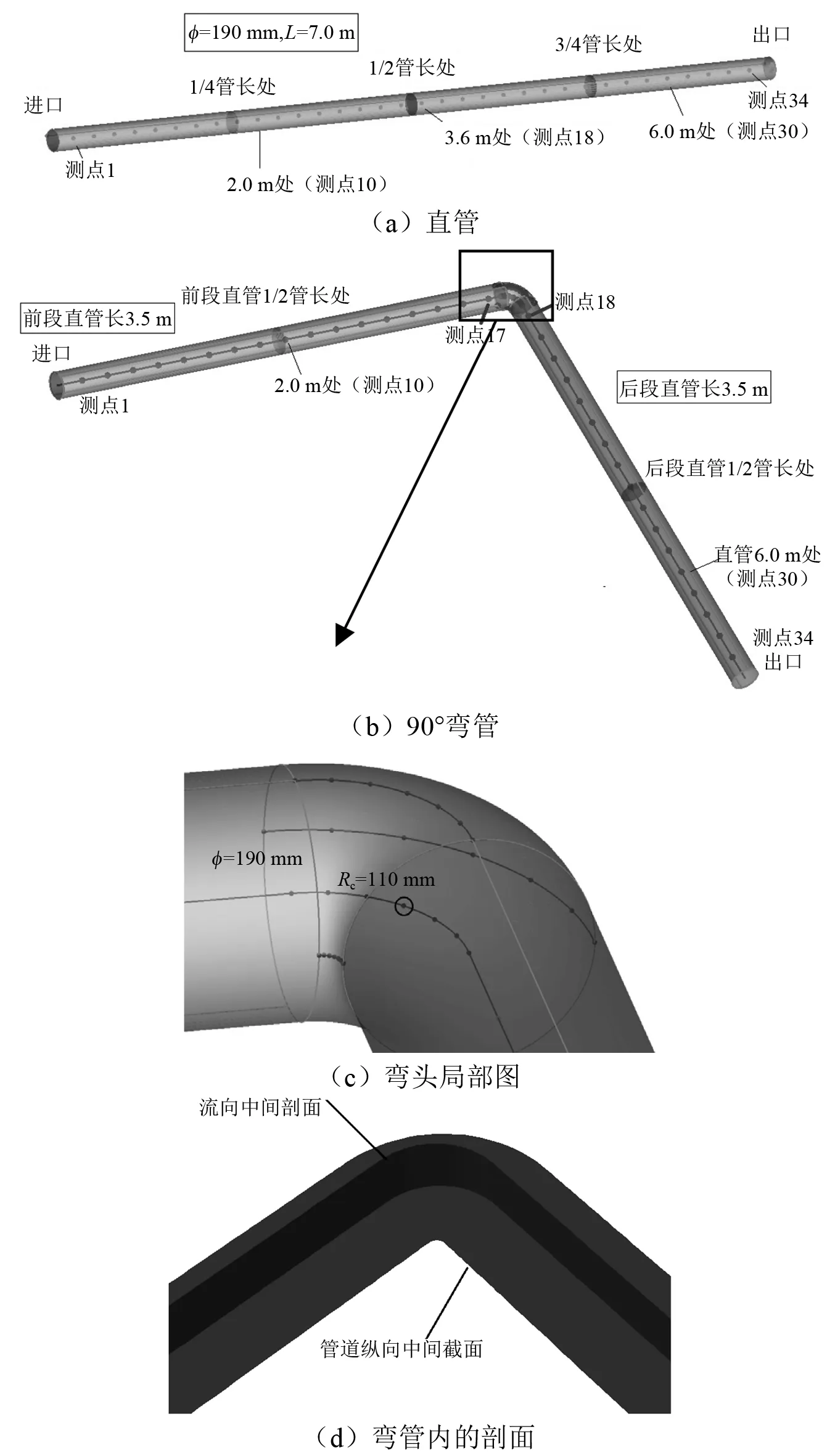
图1 所研究的直管和弯管
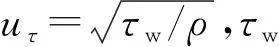

表1 计算模型网格统计
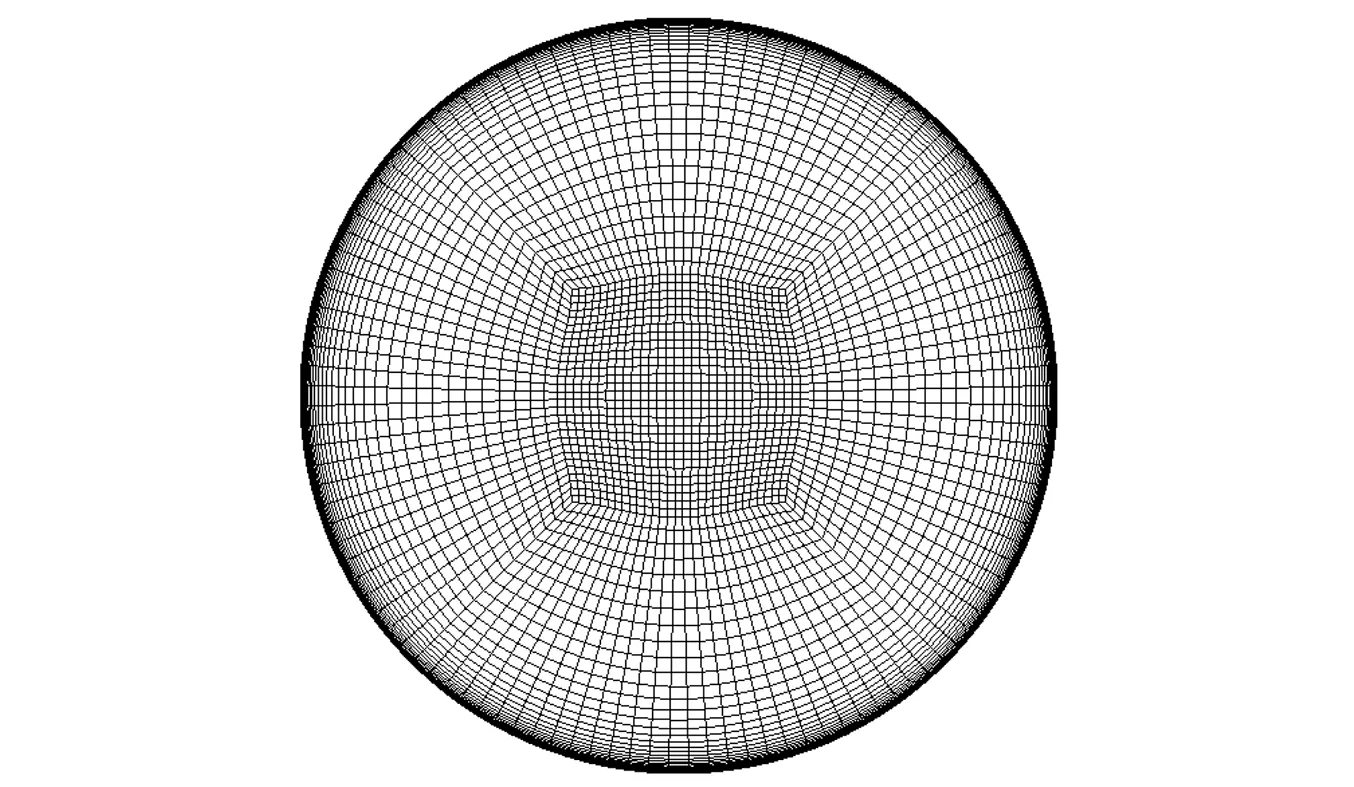
图2 圆管截面计算网格分布
SSTk-ω湍流模型的湍动能k和耗散率ω的对流-扩散方程为
(16)
(17)
式中:Gk,Gω为k,ω的产生项;Yk,Yω为耗散项;Sk,Sω为用户自定义源项;Dω为交叉-扩散项;扩散系数Γk=μ+μt/σk;Γω=μ+μt/σω;σk和σω为k,ω湍流Prandtl数;μt为湍流黏性系数,定义为
(18)
式中:S为应变率张量; 系数α1=0.31;α*系数用于衰减湍流黏度;F2为第二混合系数,它在边界层内取值为1而在自由剪切层内取值为0。
2.2 边界条件及计算方法
进口处施加随时间正弦变化的总压力边界条件:p=131+23.6sin(3 644.24t),基频为580 Hz。该边界条件模拟某台具有12个叶片转速为2 900 r/min的风机出口压力脉动。风机内部旋转叶片产生的流场脉动,风机出口处的压力脉动包括水动力压力脉动和声学压力脉动,而前者为主要分量。管道进口的湍流条件设为湍流强度5%,水力直径为0.19 m。出口设置为压力出口条件,平均静压为0。管道壁面使用无滑移壁面边界条件。
由于弯管流动的压力损失比直管大,所以弯管流量比直管流量小。计算得到直管内平均流速为11.3 m/s,弯管为9.267 m/s,对应的Re分别为1.471×105和1.206×105,为湍流流动。
压力与速度耦合采用SIMPLE算法,动量、湍动能k以及耗散率ω方程均采用二阶迎风格式。时间步长设为2.020 47×10-5,即一个周期分为2 048个时间步。迭代敛残差值设置为10-6。经过大约8个周期,计算趋于稳定后进行数据采集及保存,同时打开FLUENT瞬态计算中的Statistics选项以得到各时间步的速度、压力的时均值和均方根值,共采集了16个周期的数据。
基于弯管流动更为复杂这一事实,对网格无关性、时间步长无关性以及数值模拟的准确性进行验证。分别对单元数151.7万、267.7万、419.2万三套网格进行计算,计算稳定后进行时间步的平均,得到时均流场。用网格无关性验证说明的弯头处平均压力场,如图3所示。由图3可知,三套网格的计算结果基本相同,267.7万、419.2万网格的结果非常接近,说明267.7万网格的流场可视为网格无关。同时对267.7万网格,进行时间步长为1.01×10-5s的计算,比较图3(c)和图3(d)可知流场几乎无区别,表明时间步长已经足够小。
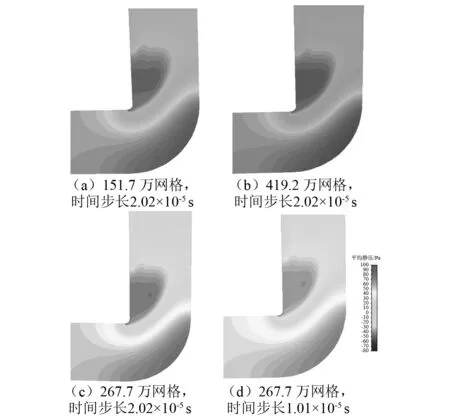
图3 网格无关性验证弯头处平均压力场
3 结果分析
3.1 平均流场
沿管道中心的平均静压分布,如图4所示。由于两个管道入口处总压相等(都为131 Pa),而直管内的流动速度大,所以静压较低。对于直管,中心线上的静压分布与周围壁面分布基本一致(横截面上压力分布均匀),所以图中仅显示中心线处的数值,可以看出平均静压基本上呈线性下降。对于带90°弯头的弯管,显示了中心线处及以上侧、内侧、外侧边界层中的静压分布,可以看出上游直管静压基本上呈线性下降直到靠近弯头进口截面。在弯头进口附近,管壁内侧面压力有所下降,外侧面则上升,中心线和上侧面基本一致。在弯头下游的静压先下降然后恢复,且不同部位的压力特性区别较大(横截面上压力分布不均匀),再往下游管道横截面上压力分布又恢复均匀,表现出与直管相同的分布特性。
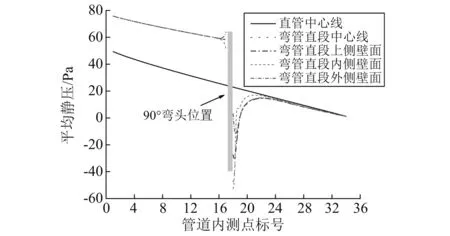
图4 沿管道流向的静压分布
为研究流动沿管道的发展情况,在管道设置了若干横截面,截面位置参见图1。这些横截面上的时均压力分布,数据取自流向中间剖面,如图5所示。由图5可知,直管横截面上的平均静压基本为常数;对于弯管,弯头附近横截面上压力分布不均匀,但远离弯头区域的横截面上压力逐渐恢复均匀。
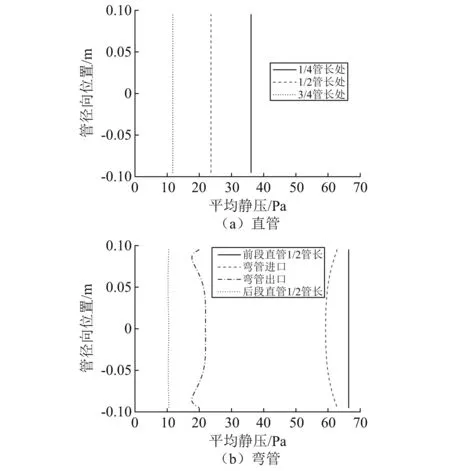
图5 管道截面上的平均压力分布
图5中对应横截面上的时均速分布,如图6所示。由图6可知,直管平均速度场为典型的管内湍流分布形状;对于弯管,90°弯头对下游直管内的速度分布影响非常明显。
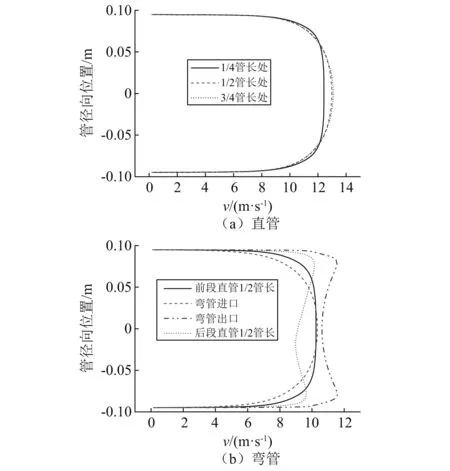
图6 管道横截面上的平均速度分布
弯头处的流向及纵向中截面上的时均流场,如图7所示,截面位置参见图1(d)。从平均静压图上可以看出,在弯头上游直管压力分布均匀,基本为平面波,在弯头附近开始复杂化。结合压力和速度场,可以看到在弯头下游管道内侧部分存在明显的低压、低速的尾迹区,该尾迹区的存在导致外侧流体流速增加,从而形成一定的射流现象,之后沿管道下游流动逐渐恢复均匀。
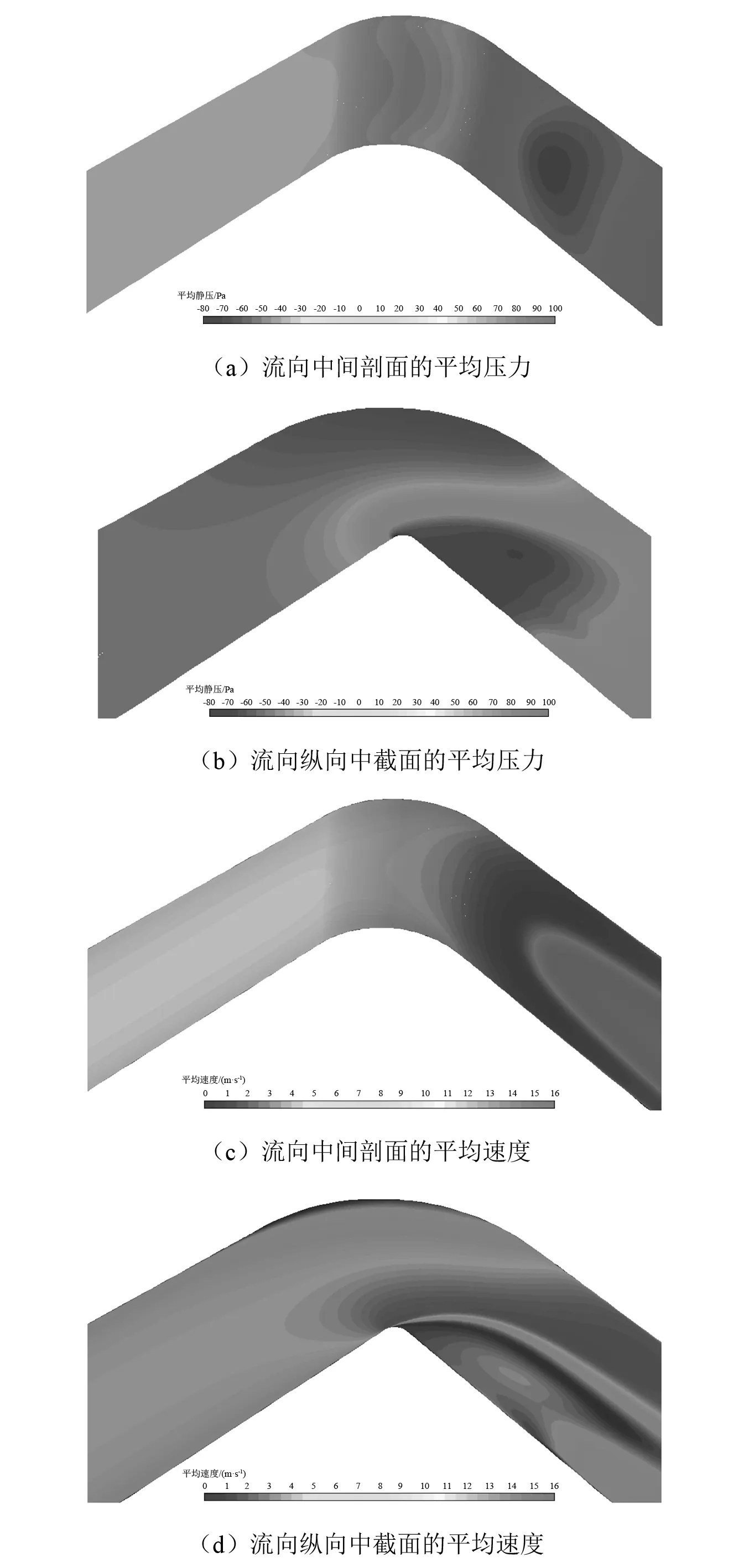
图7 90°弯头处平均流场
90°弯头中间横截面上的某一时刻速度投影矢量图,如图8所示。由图8可以明显看出二次流现象:弯头内侧流体(图中左边)因转弯离心力作用向外侧运动,而在壁面附近由于速度低离心效果不明显,流体在压力差驱动下从外侧挤向内侧,两者效果叠加最终在横截面上形成一对旋涡流。

图8 90°弯头中间横截面的二次流
3.2 脉动流场
以脉动时域信号的标准差作为脉动强度的评价标准,沿管道流动方向的压力脉动强度分布,如图9和图10所示,参考点位置参见图1。
对于直管,其壁面边界层的压力脉动与管道中心的压力脉动几乎一样,所以图中省去直管壁面附近压力脉动情况。由图9可知,直管内不可压缩流场水动力压力脉动幅度基本呈线性衰减。在出口处脉动强度为0,因为那里设置了静压为0的压力边界条件。动提高了局部压力脉动强度。弯头后直管压力脉动呈线性下降。由图10可知,尽管弯头处平均流场紊乱,但管道中心与上侧、外侧面附近压力脉动强度几乎一致,且沿管道方向线性衰减。由于弯头内侧曲率半径小,其测点上的压力脉动强度分布稍有不同,脉动强度线性衰减斜率小,这归因于弯头内侧出口处流场更为紊乱。
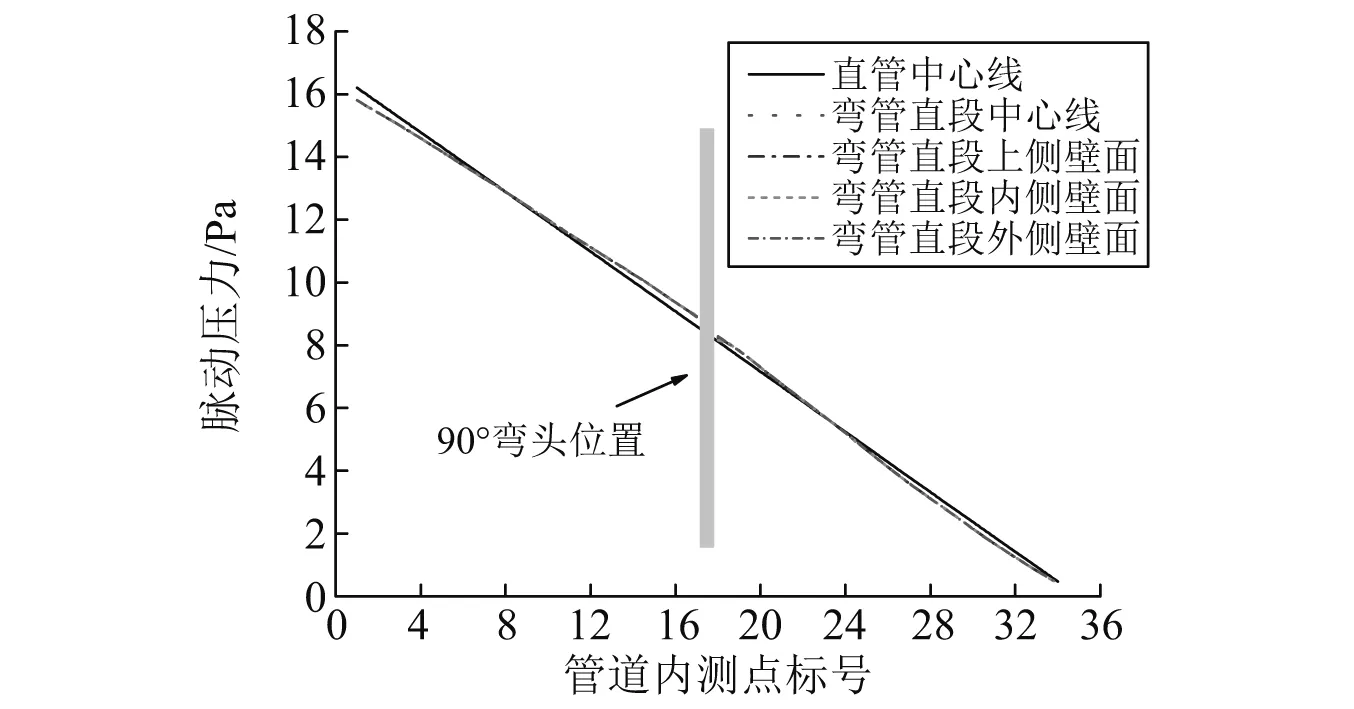
图9 沿管道压力脉动强度分布
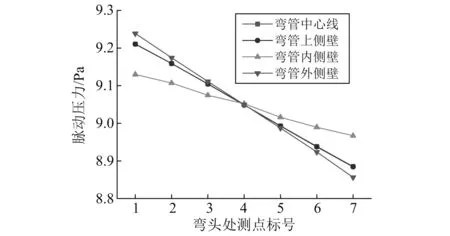
图10 90°弯头处压力脉动强度分布
对于弯管内流动,由于90°弯头的影响,使上半截直管内的压力脉动降低速度比直管慢。弯头处流场扰
沿管道流动方向的脉动流场,如图11和图12所示。可以看出对于直管,压力脉动在横截面上基本一致,呈一维形式,而速度脉动在横截面上并不均匀。对于弯管,脉动流场也有类似结论:尽管有90°弯头存在,其内部的压力脉动仍呈一维形式;速度脉动相当紊乱,并且弯头后直管内速度脉动增加。
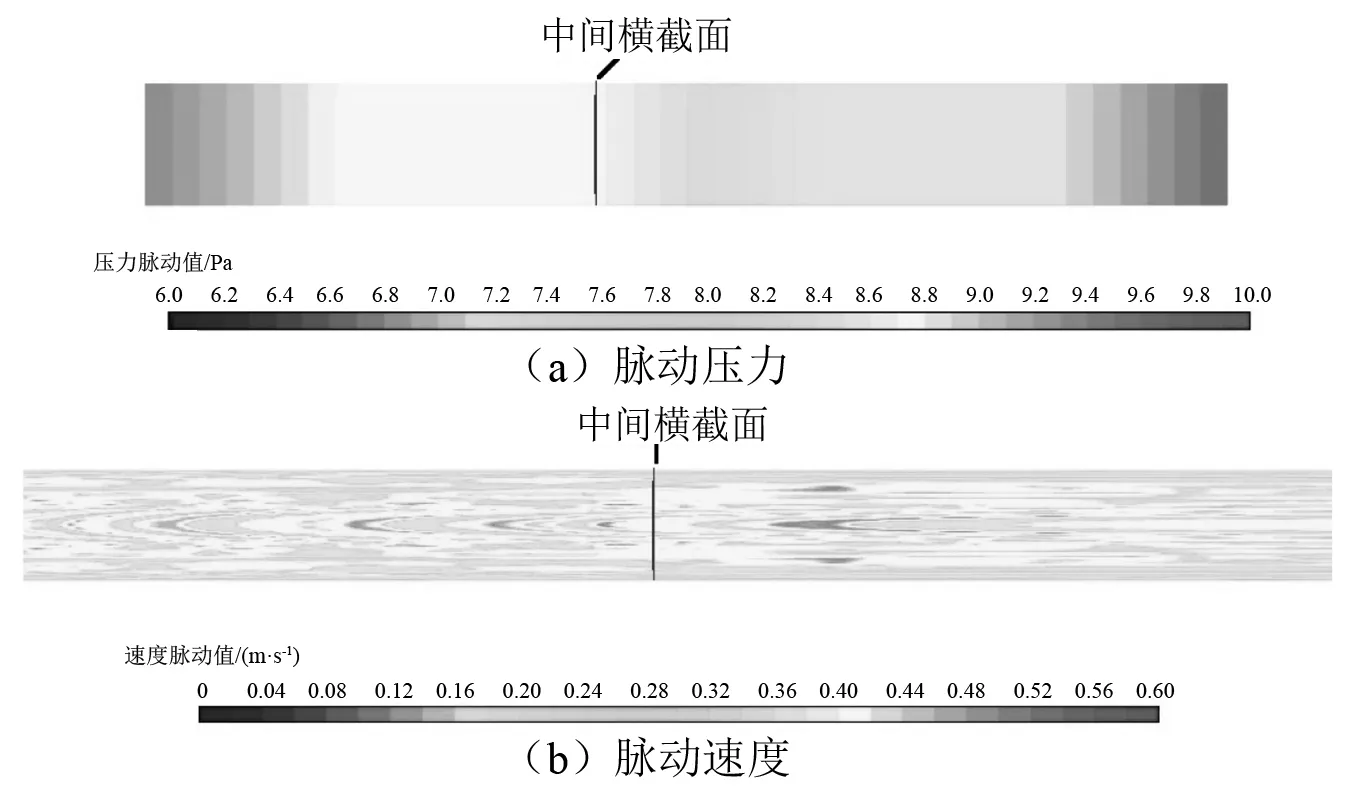
图11 直管内流向中间截面上的脉动流场

图12 弯管内的脉动流场
管内中心线上3个测点的压力脉动时间信号,如图13所示。其距离指离管道入口的直管距离,弯头拐角处指弯头中间点(见图 1中圆圈内的点)。可以看出直管内各处的压力脉动几乎为正弦波,沿管道下游脉动幅度逐渐下降。各点处脉动波形无相位差,这是因为不可压缩流动压力脉动(伪声)的微分方程为Poisson方程,声速为无穷大,所以声场内各点的脉动具有同步性。对于弯管,管内压力脉动大体上仍为正弦波形状,但由于弯头对流动影响,波形中夹带其他频率分量。

图13 管道内中心线上监测点压力脉动
上述直管和弯管中心处3个测点的压力脉动频谱,如图14所示。由图14可知,580 Hz基频最为突出,其低次谐波离散分量也较显著,高于9次谐波的离散分量已经不明显。弯管内流动的宽频压力脉动分量较直管大,这归因于弯头对流动的影响。整体上,沿管道压力脉动强度逐渐下降。壁面附近边界层内压力频谱与管道中心处基本一致,说明水动力压力脉动形态沿管道呈准一维方式,尽管速度场分布呈复杂三维流动。
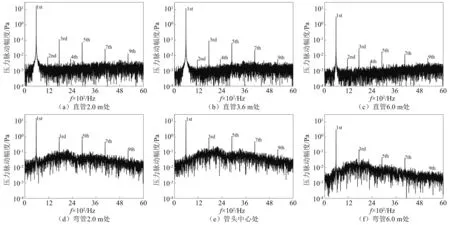
图14 管道中心线上监测点压力脉动频谱
直管和弯管弯头中间截面处测点的速度脉动频谱,如图15所示。由图15可知, 580 Hz基频及其低次谐波离散分量较明显,这是因为流体黏性壁面附近的速度脉动略低于管道中心处的速度脉动。

图15 管道内监测点速度脉动频谱
4 结 论
本文分析了管内脉动水动压力(伪声)的椭圆型微分方程,并与声波方程进行了比较。基于计算流体动力学,利用SSTk-ω湍流模型,数值研究管道入口处施加随时间正弦变化压力边界条件下管内水动压力脉动特性,得到的结论如下:
(1) 直管道内水动压力波基本上呈一维形式,其横截面上平均压力及脉动压力分布均匀。沿管道下游,压力脉动幅度线性衰减。平均速度分布为典型的管道湍流速度分布。管道内速度脉动十分紊乱,在管道横截面上分布不均匀,这与压力脉动的特性不同。
(2) 弯管内流动在90°弯头后面有明显的尾迹区,而在横截面上存在二次流。弯头对弯内流动的影响导致在弯头附近流动呈三维复杂化,局部流动扰动明显增强,使压力脉动和速度脉动幅度都有所提高。尽管弯头处流动呈复杂的三维流动,但压力脉动的传播整体上仍为一维形式。
(3) 压力脉动频谱中基频及低次谐波明显,9次谐波以上的离散分量已不明显。90°弯头使其附近流场的压力脉动和速度脉动宽频分量有所增强。由于压力脉动微分方程为Poisson方程,扰动传播速度为无穷大,所以管道各点的压力脉动信号无相位差。
