基于Copula函数的风浪多方向极限状态曲线
2021-07-22涂志斌黄铭枫楼文娟
涂志斌, 黄铭枫, 楼文娟, 李 蓓
(1. 浙江水利水电学院 建筑工程学院,杭州 310018; 2. 浙江大学 建筑工程学院结构工程研究所,杭州 310058)
ECM(environmental contour method)是多维随机环境变量联合作用下结构极限荷载效应估计的常用方法,其核心思想是在具有指定超越概率的环境变量极限状态曲线上搜寻荷载效应极值作为结构的极限荷载效应[1],在海洋工程[2-3]、地震工程[4]和风工程[5]中均有广泛的应用。其中构造具有指定超越概率的多维随机环境变量极限状态曲线是ECM的基础。
Rosenblatt变换是极限状态曲线构造的一般方法。该方法首先在标准正态空间中构造一个与可靠指标对应的圆,再将该圆映射到物理空间中得到具有指定超越概率的随机环境变量极限状态曲线[6]。根据该变换,Agarwal等[6]和Valamanesh等[7]分别构造了某海域平均风速和有效波高的极限状态曲线;Saranyasoontorn等和Haver等[8]分别构造了某海域有效波高和谱峰周期的极限状态曲线。在以上研究中随机变量的联合分布由主变量的边缘分布和其他变量的条件分布表达,采用Rosenblatt变换构造极限状态曲线较为简便。若随机变量的联合分布由传统联合分布模型(如皮尔逊Ⅲ型分布[9]、二维Gumbel逻辑分布[10]、Nataf分布[11-12]等)或Copula函数[13-15]表达,在Rosenblatt变换之前则需先根据联合分布求解条件分布。然而由于以上联合分布模型采用了较为复杂的相关结构,条件分布的求解较为困难。Huseby等[16-17]基于蒙特卡洛模拟(Monte Carlo simulation,MCS)提出通过求解随机样本具有指定超越概率的凸集的超平面来构造极限状态曲线,直接避免了Rosenblatt变换需要求解随机变量条件分布这一难题,提高了极限状态曲线构造的可行性。然而针对该方法有三点需要说明:①随机样本的生成依赖于随机变量的联合分布模型,若联合分布模型复杂,则随机样本的生成算法也复杂;②求解精度和效率与样本容量密切相关,若样本容量较小,极限状态曲线在局部将出现封闭环;③该方法将凸集边界近似为所有超平面构成的封闭曲线,使所求极限状态曲线略大于真实极限状态曲线。Vanem等[18]详细比较了两种构造极限状态曲线的方法,提出了各自的适用范围。
风向和波向是海洋环境中重要的随机变量,对海洋结构设计有重要影响[19-20]。Zhang等[21]研究发现各方向的平均风速和有效波高可能服从不同的边缘分布模型,二者的相关关系也不尽相同。季新然等[22]认为波向分布对波浪爬高具有较大的影响,在实际设计中若不考虑波向的影响可能低估或高估群墩周围的波浪爬高。吴家鸣等[23]在研究波向对导管架平台主桩应力响应的影响时发现,存在一个最不利波向使主桩应力最大。同时大量风向与建筑物抗风可靠性的研究表明若不考虑风向效应,极值风速和结构设计风荷载均有可能被高估[24-27]。然而目前与风向和波向对风浪极限状态曲线及海洋结构极限荷载效应影响相关的报道还不多见。
本文在Rosenblatt变换的基础上引入Copula函数,提出了二维随机变量极限状态曲线构造的改进方法;结合风浪同步观测数据研究了风向与波向对风浪极限状态曲线的影响;估计了某导管架平台各方向的基底剪力极限荷载效应及对应的平均风速和有效波高取值,并得到了几点有益的结论可供海洋结构设计参考。
1 基于Copula函数的极限状态曲线
1.1 Rosenblatt变换
设二维随机变量E=(E1,E2)服从[0,1]2内的独立均匀分布;Z=(Z1,Z2)为标准正态空间中相互独立的二维随机变量;ei=Φ(zi)(i=1,2),Φ(·)为一维标准正态分布函数;X=(X1,X2)为物理空间中具有任意相关关系的二维随机变量。根据Rosenblatt变换有
(1)
式中:F1(x1)为变量X1的边缘分布函数;F2|1(x2|x1)为变量X2的条件分布函数,由X2的边缘分布和X1与X2的相关结构决定。对式(1)求逆可得
(2)
在标准正态空间中极限状态曲线是半径等于可靠指标β的圆,即
(3)
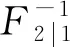
1.2 Copula函数的基本理论
Copula函数是一种构造联合分布模型的工具系统,可构造具有任意相关关系和边缘分布的多维随机变量的联合分布函数,并将现有的多种联合分布模型纳入其中,如Gumbel分布、Nataf分布等。设二维随机变量U=(U1,U2)服从[0,1]2内的独立均匀分布,且ui=Fi(xi)(i=1,2),那么根据Copula函数,二维随机变量X的联合分布函数F(x1,x2)可表达为
F(x1,x2)=C[F1(x1),F1(x2)]=C(u1,u2)
(4)
式中:C(·)为Copula函数;F2(x2)为变量X2的边缘分布函数。若F1(x1),F2(x2)均连续,则C(·)唯一确定。由式(4)可知,当随机变量的边缘分布已知时,Copula函数的作用在于确定变量之间的相关结构。
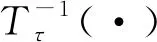

表1 常用二维Copula函数族及其典型函数
采用Copula函数构造随机变量的联合分布模型时,同时满足以下两个条件的Copula函数称为最优Copula函数:①Ui=Fi(xi)能准确地描述Xi的边缘分布特性;②由Copula函数确定的相关结构能准确描述各随机变量间的相关关系。目前常用的最优Copula函数评价准则为AIC(Akaike information criterion),其表达式为[28-29]
(5)
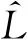
1.3 改进方法
根据Copula函数理论的相关研究,条件分布函数F2|1(x2|x1)与Copula函数的关系为[30]
(6)
式中,C2|1(u2|u1)为条件Copula函数。将式(6)代入式(1)中的第2式可得
e2=C2 |1(u2|u1)
(7)
那么,
(8)
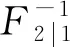
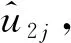
2 风浪实测数据与样本选取
本文以纽约东海岸附近63115号海洋观测站(北纬40.50°,西经-72.92°)的风参数和波浪参数观测记录为统计样本,数据来源于美国陆军工程兵团工程研究发展中心官网。该统计样本的记录时间为1980年1月1日—2014年12月31日,但部分时间段的统计样本有缺失。各参数均同步记录,每小时记录一次。同步提取平均风速日极值v和对应的有效波高Hs、风向φv及波向φH作为风浪多方向极限状态曲线分析的样本。风向与波向之差(φv-φH)的角直方图,如图1所示。其中风向和波向均为记录时间处的瞬时值。图1表明风向和波向的差异较小。根据规范IEC 61400-3和Zhang等的建议,当风向和波向差异较小时,在风浪联合作用分析中可认为风向和波向保持一致。将风向归类到8个角度区间,其玫瑰图如图2所示。由图2可知:日极值风速的风向记录在SE,S,SW和W方向上的频率较高,分别为16.57%,17.42%,13.37%和18.17%;而在NW,N,NE和E方向上的频率较低,分别为10.94%,9.52%,7.59%和6.40%。由于波向与风向的偏差较小,图2也表达了波向在各方向上的分布频率。SE(深色)、W(深色)及全方向(浅色)3个方向上的日极值风速及对应有效波高散点图,如图3所示。由图3可知:①不同方向上散点的尾部特性有所不同,在W方向上尾部较为厚重,分布范围为[15 m/s, 20 m/s],在SE方向上尾部轻且较为离散,分布范围为[10 m/s, 20 m/s];②在3个方向上平均风速和有效波高的线性相关系数分别为ρSE=0.770 1,ρW=0.826 3和ρAll=0.744 5,均具有较强的相关性,但相关程度又有所不同。这说明不同方向上平均风速和有效波高的边缘分布特性和相关关系均有所不同。
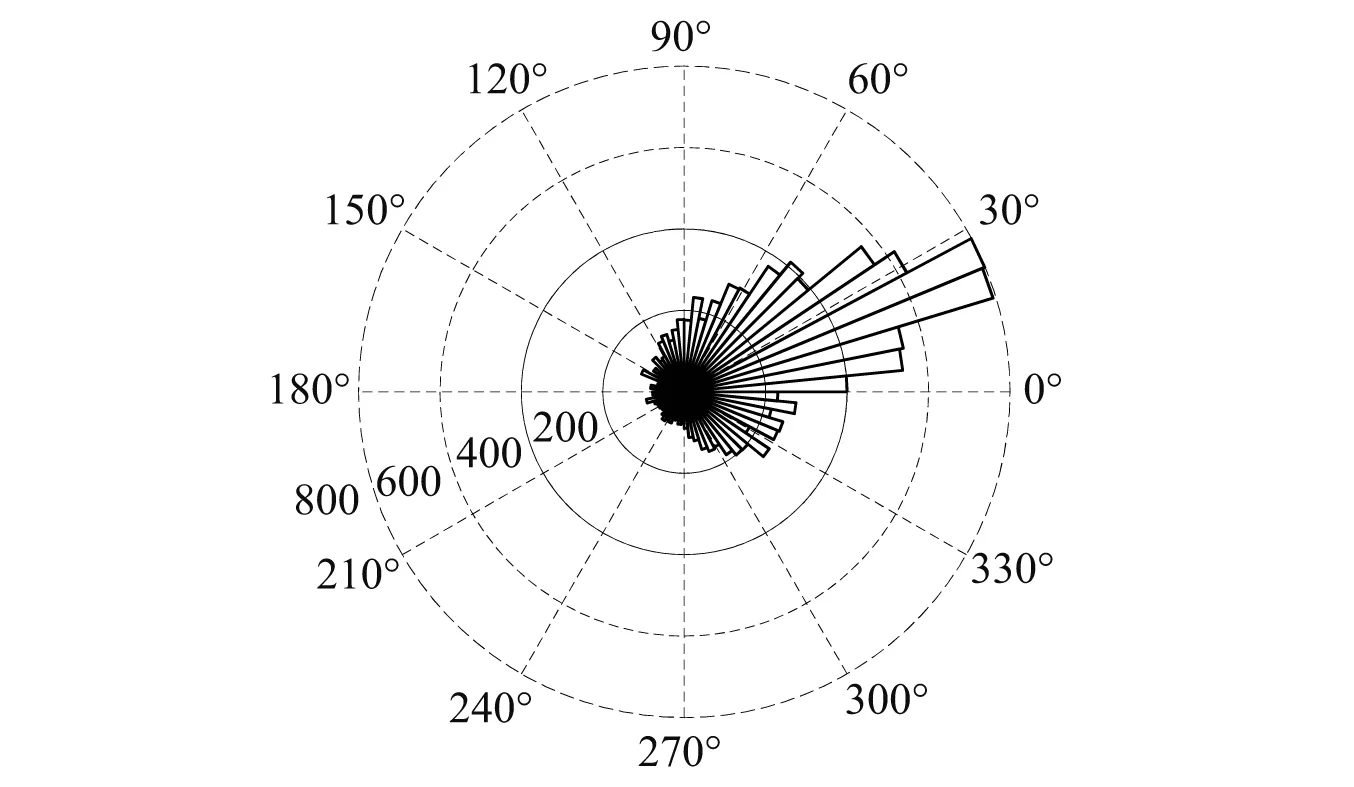
图1 风向与波向之差角直方图
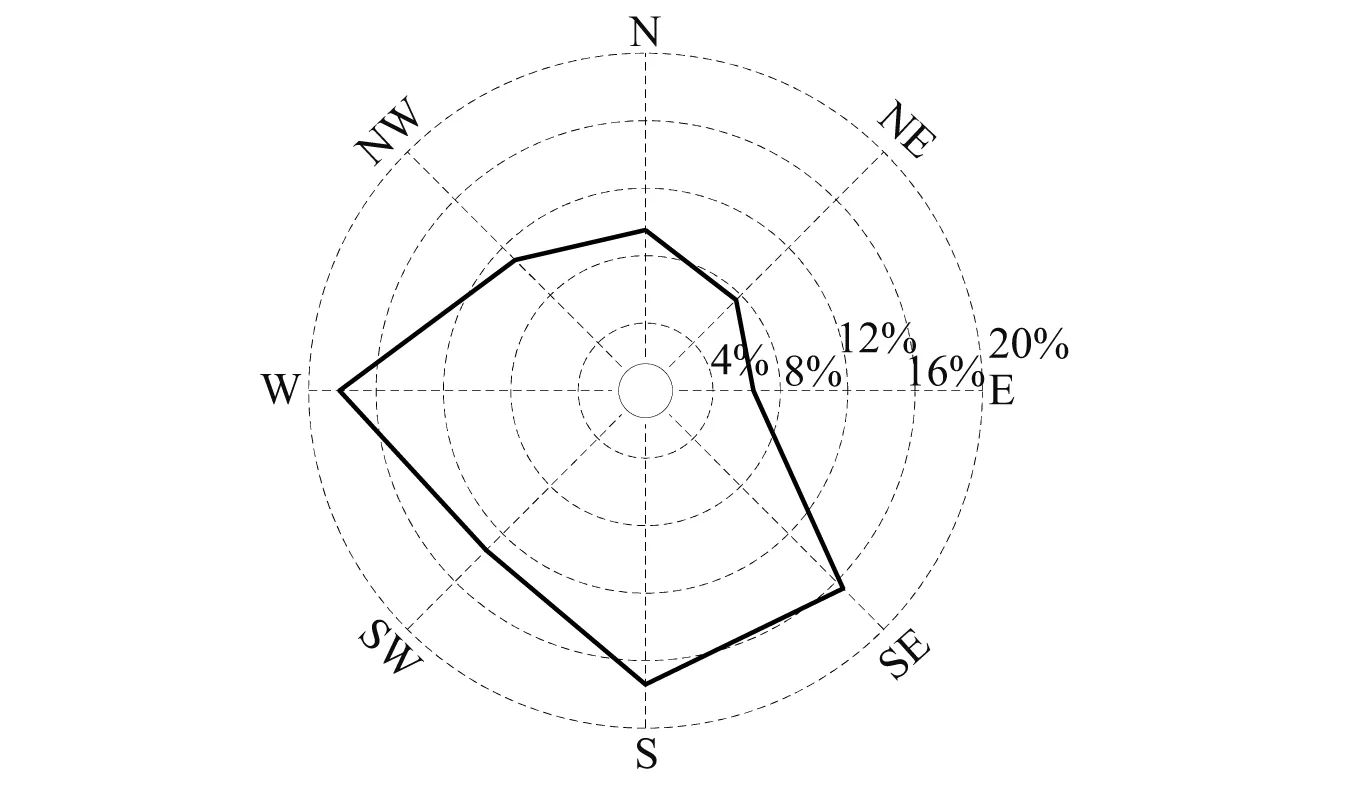
图2 日极值风速对应风向玫瑰图

图3 日极值风速及对应有效波高散点图
3 风浪多方向极限状态曲线
3.1 风浪边缘分布
目前平均风速和有效波高极值的边缘分布多采用Weibull分布、Gamma分布和Lognormal分布来描述,其表达式分别为:
Weibull
(9)
Gamma
(10)
Lognormal
(11)


表2 SE方向上日极值风速和有效波高边缘分布估计结果
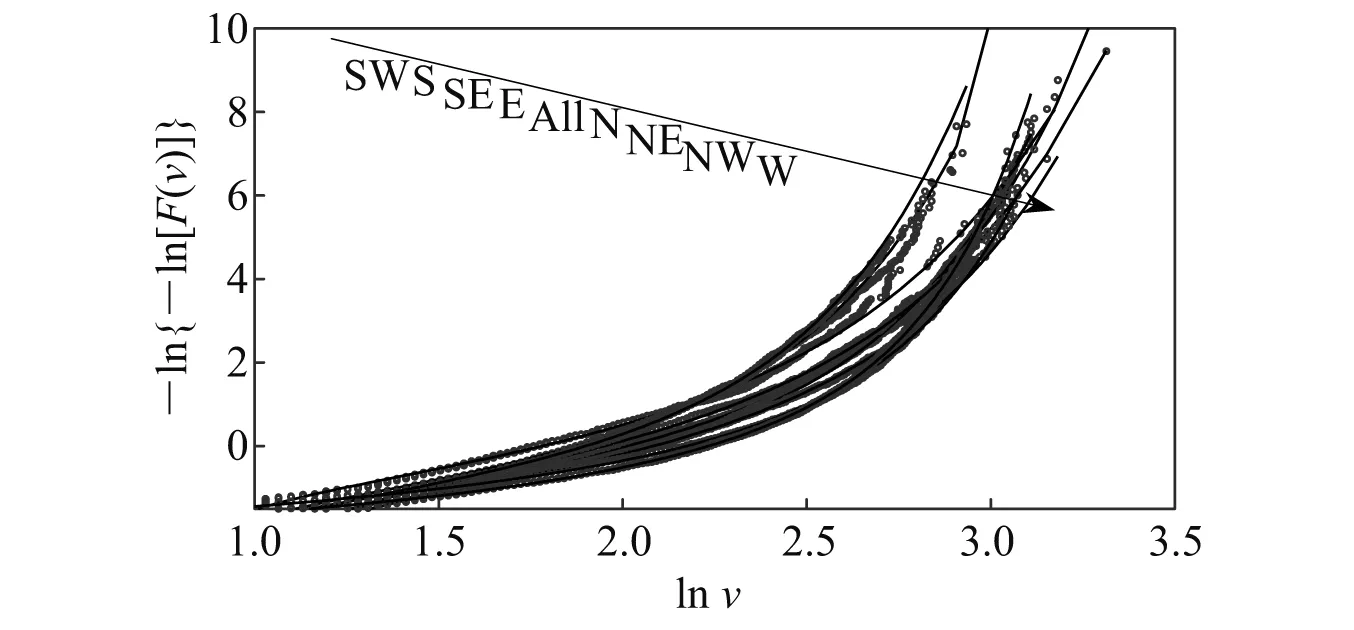
图4 各风向下日极值风速的边缘分布拟合

图5 各风向下同步有效波高的边缘分布拟合
3.2 风浪联合分布
从表1中选择最优Copula函数来构造日极值风速和同步有效波高的联合分布模型。采用伪极大似然估计法估计各Copula函数的参数[31],并根据AIC准则选择最优Copula函数,结果如表3所示,其中括号外的数据为参数估计值,括号内的数据为AIC值。由表3可知,除NW方向的最优Copula函数是Plackett Copula外,其他方向的最优Copula函数均为Gumbel Copula。
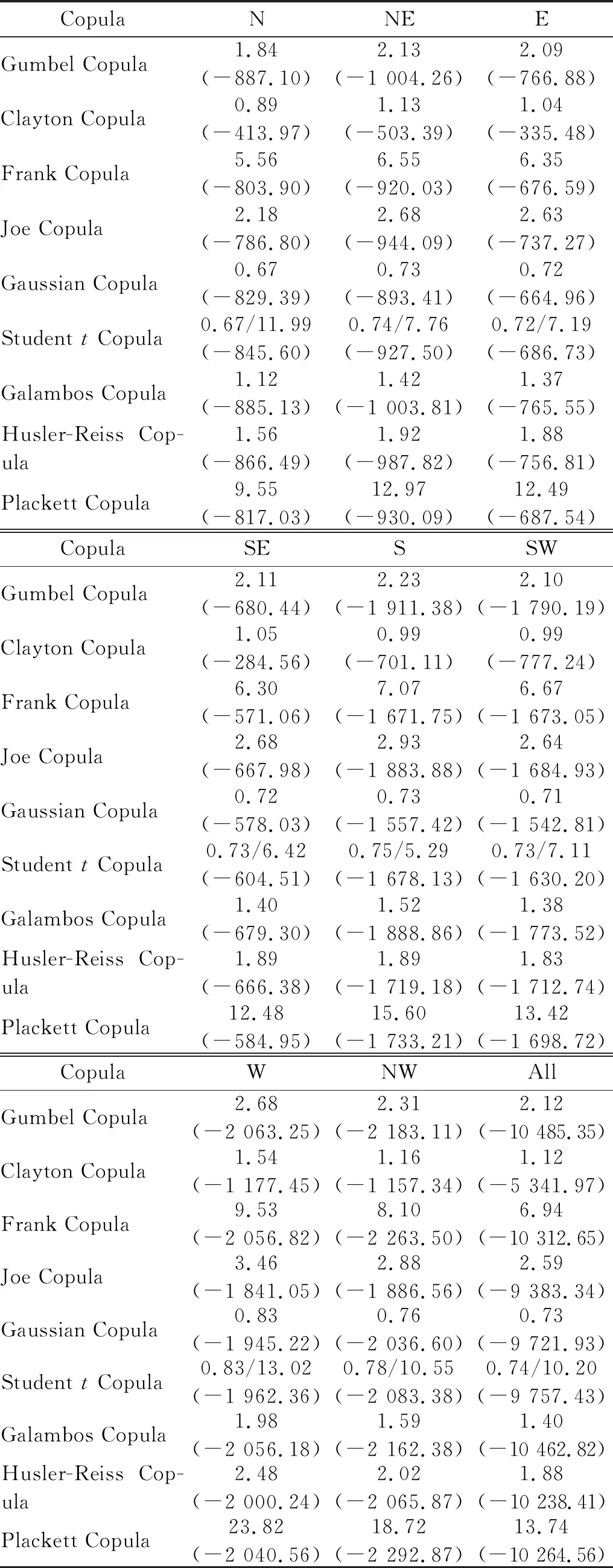
表3 日极值风速和同步有效波高联合分布模型参数估计值及AIC值
SE,W和All 3个方向的日极值风速和同步有效波高联合分布,如图6所示。由图6可知,3个方向的峰形均呈现出非对称性但并不相同,具体表现为:①峰值的取值坐标不同,SE,W和All方向峰值对应的日极值风速和同步有效波高分别为(6.5 m/s,1 m),(11.5 m/s,1.6 m),(8.7 m/s,1.2 m);②与SE和All方向相比,W方向的峰形较陡且狭长。以上不同是因为各方向的日极值风速和同步有效波高的边缘分布及相关性均不相同,需要采用不同的模型来描述其联合分布。
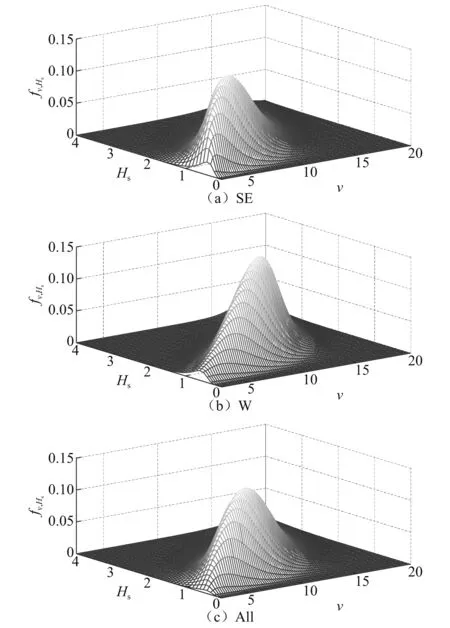
图6 日极值风速和同步有效波高的联合分布
3.3 改进方法的验证
考察数值算法中角度离散点数n对基于Copula函数的二维随机变量极限状态曲线的影响。当步长Δθ=3°,Δθ=6°,Δθ=10°和Δθ=15°(对应n=120,n=60,n=36,n=24)时,SE方向日极值风速和同步有效波高的极限状态曲线(重现期T= 50 a),如图7所示。由图7可知,当n=60时极限状态曲线趋于光滑。对其他各方向、各重现期下的极限状态曲线进行考察可得到相同的结论。因此在本文中采用数值算法计算基于Copula函数的日极值风速和同步有效波高的极限状态曲线时角度离散点数取n=60。
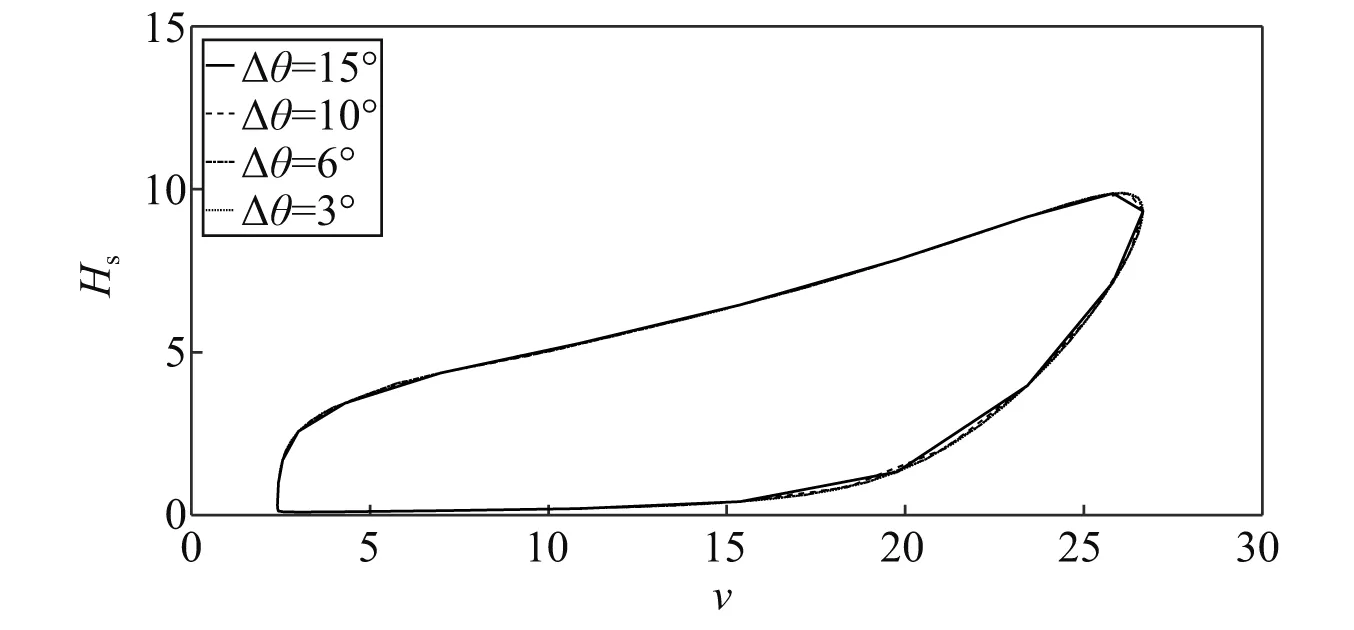
图7 不同步长下T=50 a时SE方向日极值风速和同步有效波高的极限状态曲线
本文将对比基于Copula函数的极限状态曲线和基于MCS的极限状态曲线,以验证改进方法的准确性。基于MCS的极限状态曲线构造方法由Huseby等提出,其基本步骤为:①根据二维随机变量的联合分布模型生成大量统计样本;②在统计样本的基础上构造一个超越概率为Pe的凸集,并在[0,2π)内寻找其超平面;③求解相邻两超平面的交点并依次连接即可得到极限状态曲线。按照以上步骤构造重现期T=1 a,T=20 a,T=50 a时各方向上日极值风速和同步有效波高的极限状态曲线。由于日极值风速对应的统计时长为24 h,重现期T与超越概率Pe的换算公式为Pe=1/365.25/T,T=1 a,T=20 a,T=50 a对应的超越概率分别为Pe=2.7×10-3,Pe=1.37×10-4,Pe=5.48×10-5。根据日极值风速和同步有效波高的最优边缘分布及最优Copula函数生成统计样本,超平面及其交点的求解公式为

(12)
(13)

各重现期下SE方向上基于Gumbel Copula函数的日极值风速和同步有效波高极限状态曲线,见图8。总体而言,各重现期下基于Copula函数的极限状态曲线与基于MCS的极限状态曲线差异较小。在其他方向上作相同的对比可观察到类似的现象。这表明本文提出的改进方法具有较高的可靠性。同时从整个计算过程来看,改进方法的数值算法具有较高的可操作性,克服了MCS的局限性。
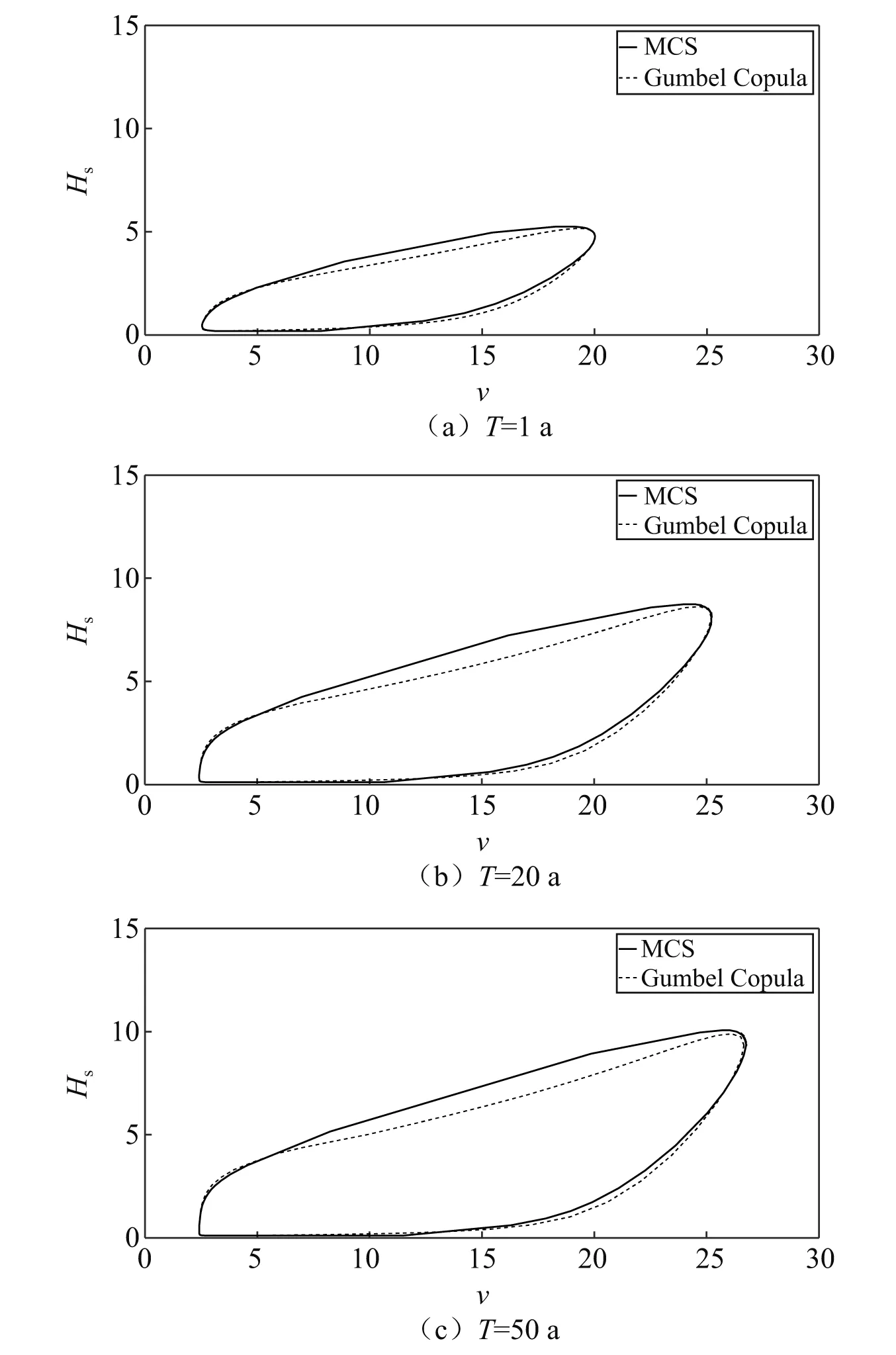
图8 SE方向日极值风速和同步有效波高的极限状态曲线
3.4 风浪极限状态曲线
当重现期T=1 a,T=20 a和T=50 a时,各方向基于Copula函数的日极值风速和同步有效波高的极限状态曲线,如图9所示。由图9可知:①随着重现期的增加,极限状态曲线的形状基本不变,但轨迹向外扩大;②除NW外,其他方向的极限状态曲线因采用同一类型的边缘分布和Copula函数构造联合分布模型而形状相似,但因边缘分布和Copula函数的参数不同而轨迹相差较大,特别是在日极值风速和同步有效波高联合取值较大的区域;③从图示箭头方向来看,在各重现期下极限状态曲线由外向内依次为NE,E,NW,SE,N,All,W,S,SW,其中All方向的极限状态曲线处于各曲线的中间位置。
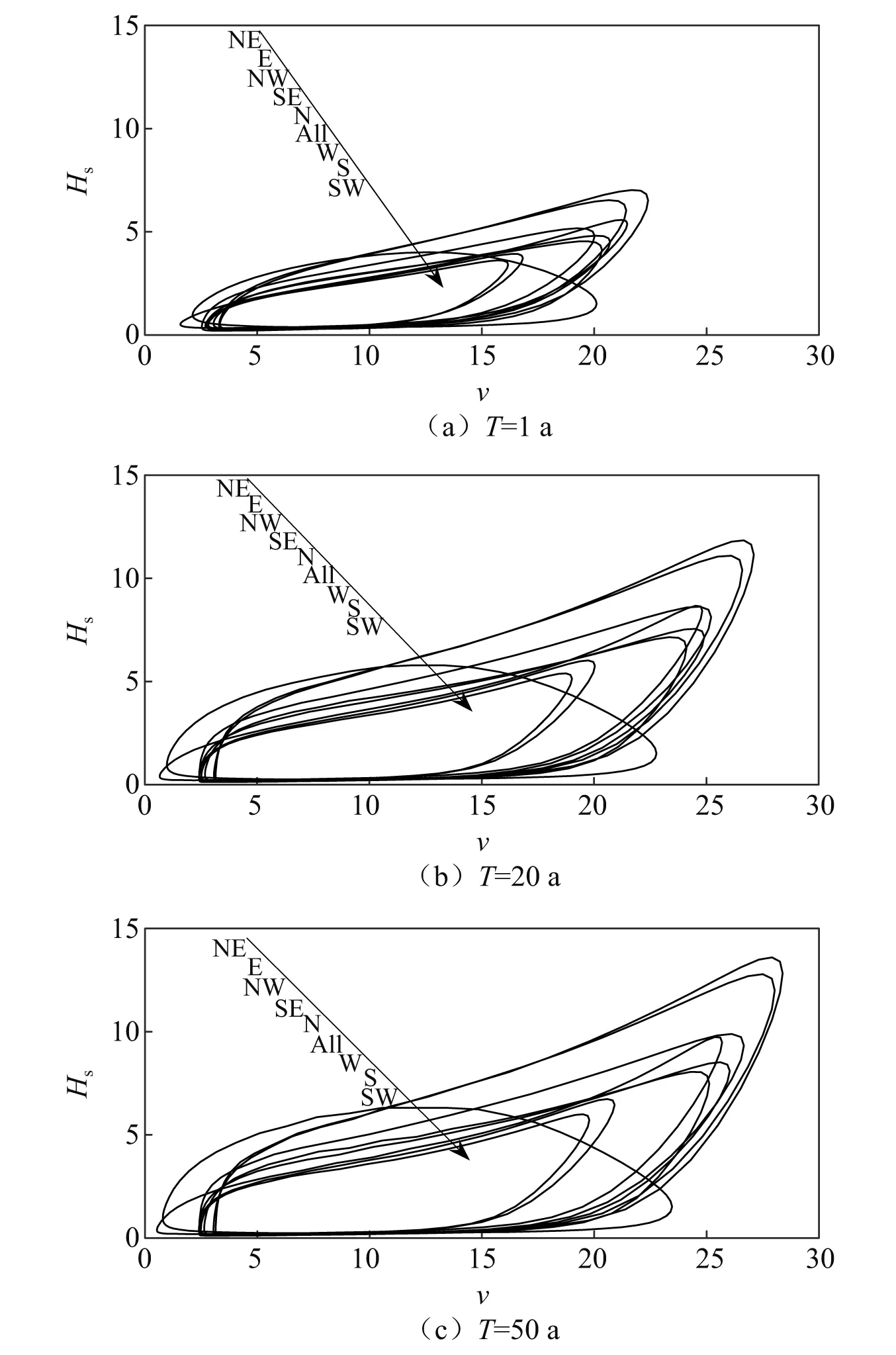
图9 基于Copula函数的日极值风速和同步有效波高的多方向极限状态曲线
采用ECM估计某导管架平台基底剪力的极限荷载效应。根据Liu等[32]的研究,某导管架平台的基底剪力Q、平均风速v和有效波高Hs的关系为
(14)
根据式(14)和图9所示的风浪极限状态曲线估计各方向不同重现期下该导管架平台的v,Hs和Q取值,结果如表4所示。与All方向相比,其他方向v,Hs和Q的取值误差r,如表5所示。由表4和表5可知:①随着重现期的增加,各方向v,Hs和Q的取值均有所增加;②在同一重现期下各方向v,Hs和Q的取值各不相同,其中NE方向的取值最大(最不利方向),All方向的取值居中,NW方向的取值最小,这与各方向风浪极限状态曲线的轨迹分布相符;③与All方向相比,NE,E,SE和W 4个方向v,Hs和Q的取值偏大,其中在NE方向,当T=50 a时三者的误差分别为8.98%,60.00%和141.18%;④与All方向相比,N,S,SW和NW 4个方向v,Hs和Q的取值偏小,其中在NW方向,当T=50 a时三者的误差分别为-8.59%,-78.82%和-82.35%。尽管根据不同的风浪观测数据,最不利方向和与All方向相比各方向上v,Hs和Q的取值偏差会有所不同,但若某方向上的极限状态曲线大于All方向,那么在该方向上的v,Hs和Q的取值将偏大,反之亦然。由此可知,对导管架平台进行结构设计时,不对风、浪的方向加以区分而直接采用全方向的统计数据构造极限状态曲线并估计结构极限荷载效应,会造成不同程度的高估或低估。出现高估或低估的原因是在主风(波)向上风浪较大而在其他方向上风浪较小,直接构造All方向的极限状态曲线忽略了这一特性,得到了一个较为平均的极限状态曲线。而分方向进行极限状态曲线的构造和结构极限荷载效应的估计则考虑了风浪在各方向上的统计规律,可得到更加精确的结果。
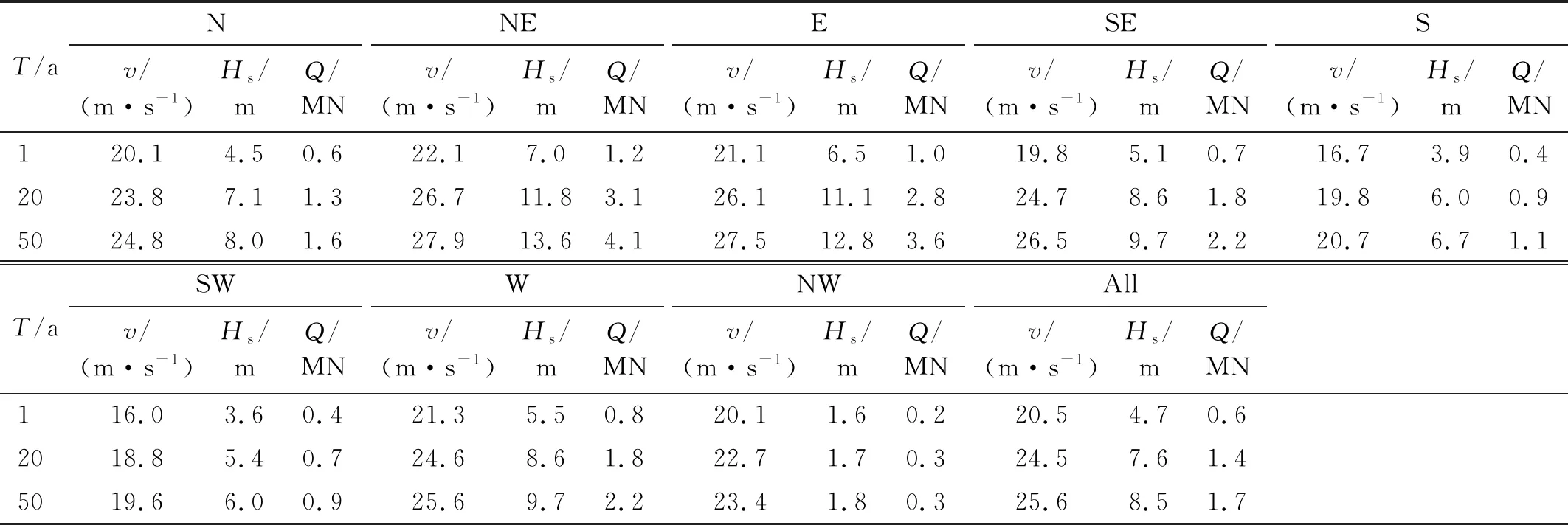
表4 某导管架平台基底剪力极限荷载效应及对应的平均风速和有效波高取值
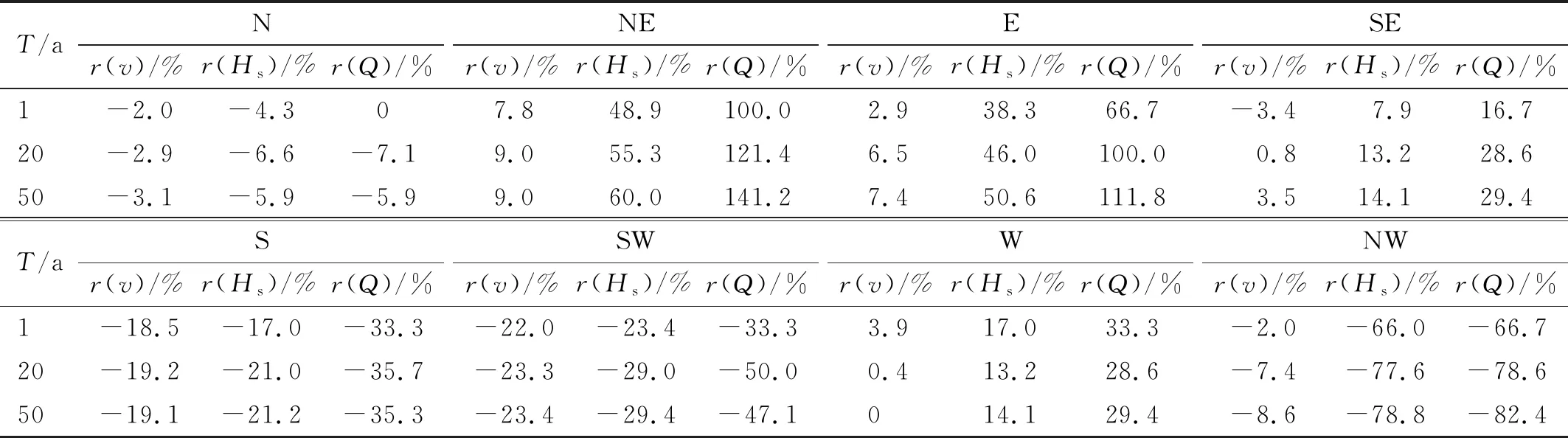
表5 某导管架平台各方向基底剪力极限荷载效应及对应平均风速和有效波高取值的误差
4 结 论
本文在Rosenblatt变换的基础上引入Copula函数,提出了二维随机环境变量极限状态曲线构造的改进方法及其数值算法;结合风浪同步观测数据研究了风浪多方向极限状态曲线,并在此基础上估计了某导管架平台的基底剪力极限荷载效应及对应的平均风速和有效波高取值,得到了以下结论:
(1) 基于Copula函数的极限状态曲线构造改进方法及其数值算法将随机环境变量的条件分布函数及其逆函数的求解转化为条件Copula函数及其逆函数的求解,具有较高的可靠性和可操作性。
(2) 各方向的日极值风速和同步有效波高极限状态曲线轨迹呈现出较大的差异,而全方向的极限状态曲线处于各条曲线的中间位置。
(3) 各方向导管架平台基底剪力极限荷载效应及对应的平均风速和有效波高取值差异较大。与全方向相比,极限状态曲线较大方向的平均风速、有效波高和基底剪力极限荷载效应取值也较大。
