磁悬浮轴承系统的模型辨识与控制
2021-07-22周亮甘杨俊杰
周亮,甘杨俊杰
(中车株洲电机有限公司,湖南 株洲 412000)
磁悬浮轴承因具有无摩擦、无磨损以及无需润滑等一系列优点,在高速主轴、气体压缩机、人工心脏泵、飞轮储能等领域广泛应用[1]。磁悬浮轴承本质上是一个非线性不稳定系统,需要设计控制器构成闭环反馈控制。除了工业上常用的PID型控制器(比例-积分-微分控制器)及其改进类型,模糊控制、神经网络控制、滑模控制、鲁棒控制等现代控制方法也可实现磁悬浮轴承的稳定控制,控制精度取决于控制器参数[2-6]。控制器参数可以通过试错法或根据工程经验确定,也可通过极点配置法设计,极点配置法设计的控制器控制性能取决于模型的准确性。
磁悬浮轴承建模时的简化处理会导致理论模型与系统实际特性有较大差异,主要体现在两方面:1)理论模型的结构与实际系统有差异[7];2)模型参数的理论值与实际值有差异[8]。故基于模型进行控制器设计时,提高控制器性能的前提是获取精确的系统模型。
模型辨识是获取精确系统模型的方法之一,具有操作简单,辨识精度高等优点。模型辨识将辨识对象看成一个“黑盒子”,通过施加特定的激励以及测量其响应,得到准确的系统输入输出关系。模型辨识分为两大类:1)已知系统的模型结构,只需通过辨识确定模型的参数值;2)模型的结构和参数均未知,两者都需要通过辨识确定。如文献[9]采用基于转子不平衡响应的方法对磁悬浮轴承的刚度和阻尼系数进行辨识。文献[10]采用电磁力测量法和自由振荡法对磁悬浮轴承的电流刚度和位移刚度系数进行辨识。为了获取电流刚度和位移刚度的精确值,文献[8]采用开环辨识的方法,文献[11]采用了基于LMS(自适应滤波)算法的在线辨识方法,这些辨识都属于模型的参数辨识。而为了得到精确的系统模型,模型结构辨识非常关键。如文献[12]通过对一个磁悬浮工作平台进行辨识,得到了系统的精确传递函数,并基于此模型重新设计控制器,优化了控制性能。文献[13]通过频域辨识方法,对实心结构磁悬浮轴承进行辨识,得到了系统的分数阶模型,并基于辨识模型设计了分数阶控制器,控制性能进一步提升。文献[14]对叠片结构和实心结构磁悬浮轴承进行系统辨识,得到了两者的精确模型,并做了对比,基于模型差异又讨论了实心结构中涡流的影响。
由上述分析可知,模型辨识法在获取系统特性、优化控制性能方面都起到了重要作用。在此基于理论模型设计了PID控制器,实现对磁悬浮轴承系统的控制。为优化控制性能,采用频域辨识法对实际系统进行模型辨识,并对辨识数据进行模型拟合。得到精确的系统模型后,重新设计控制器对转子进行悬浮控制。最后对模型辨识的结果进行分析,并对2种控制器的控制性能进行对比。
1 建模与PID控制
以某四自由度磁悬浮轴承系统为研究对象,如图1所示,其包括转子、2套径向磁悬浮轴承、位移传感器、保护轴承等零部件。径向磁悬浮轴承为转子提供径向无接触支承,位移传感器检测转子的位移变化。保护轴承通常为常规轴承,在转子未悬浮时起支承作用,在转子悬浮后因故障发生跌落时则起到保护作用。
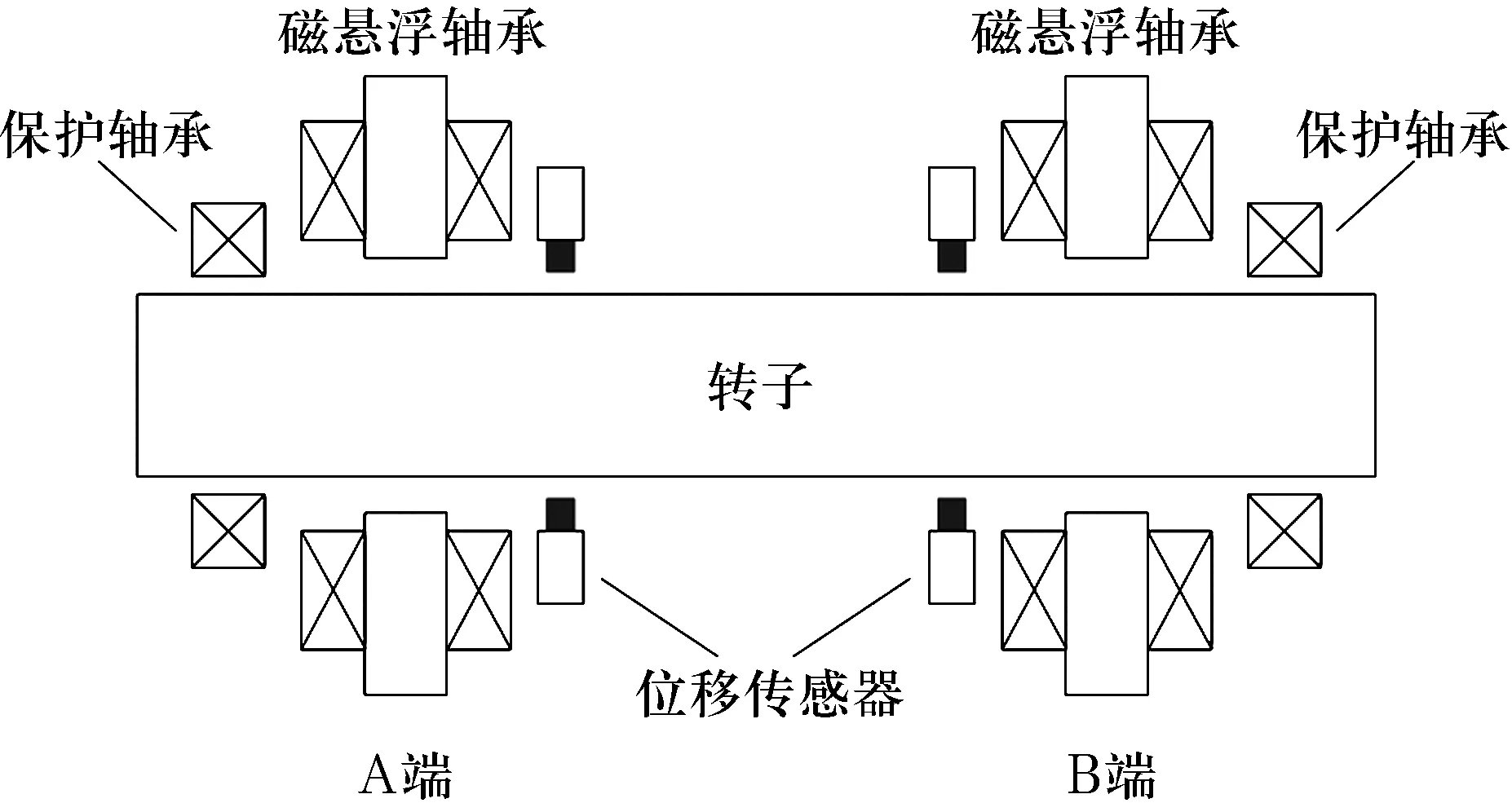
图1 四自由度磁悬浮轴承系统示意图Fig.1 Diagram of four-DOF active magnetic bearing system
2套径向磁悬浮轴承均为八磁极叠片结构(图2),图中:x0为磁悬浮轴承转子与定子之间的额定间隙,i0为线圈偏置电流。以竖直方向为例说明其工作原理,当转子偏离平衡位置时,位移传感器检测转子位移x,并将信号传送至控制器,控制器根据控制算法计算控制信号,控制信号经功率放大器转换为作用在电磁线圈上的控制电流i,电磁铁产生可控的电磁力,迫使转子回到平衡位置,从而维持转子的稳定悬浮。
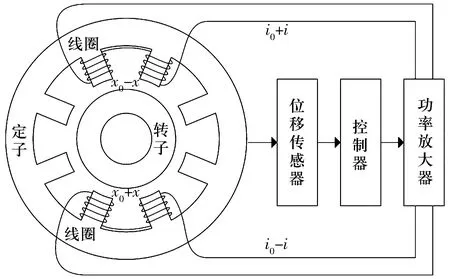
图2 八磁极径向磁悬浮轴承结构示意图Fig.2 Structure diagram of eight-pole radial active magnetic bearing
图2结构在竖直方向的电磁力为[1]
(1)
式中:k为电磁力系数,与电磁铁的结构和尺寸有关。
(1)式在平衡位置(x=0,i=0)处泰勒展开,并略去高次项,可得到电磁力的线性表达式。拉普拉斯变换后得到磁悬浮轴承在一个自由度上的开环传递函数为
(2)
式中:m为转子质量;ki为力-电流系数;ks为力-位移系数,与电磁铁的结构参数有关;s为拉普拉斯算子。
(2)式为电流控制下磁悬浮轴承的理论模型。对于文中径向磁悬浮轴承,取m=60 kg,ki=2 283.4 N/A,ks=4.57×106N/m。
(3)
式中:A0,B0,B1,C0为控制器参数。
针对图1的磁悬浮轴承系统,设计了4个控制器对4个自由度进行分散控制。控制器参数通过极点配置法确定,实际控制时根据控制效果做适当调整。
磁悬浮轴承试验平台如图3所示,控制硬件包括磁悬浮轴承位移采样电路、数字信号处理模块及开关型功率放大器,转子四自由度的悬浮位移变化通过示波器显示。试验表明设计的PID控制器能实现转子的稳定悬浮,稳定悬浮后的位移曲线如图4所示(x轴为时间,每格表示100 ms,y轴为位移,每格表示500 mV),由图可以看出:转子实现了稳定悬浮,但位移曲线波动比较明显,A端竖直方向位移波动最大,其峰值为61.6 mV,根据标定关系,对应位移波动量14.67 μm。这是由于(3)式是基于(2)式的理论模型建立的,理论模型与实际系统之间存在误差,导致控制精度较低。

图3 磁悬浮轴承试验平台Fig.3 Test rig of active magnetic bearing
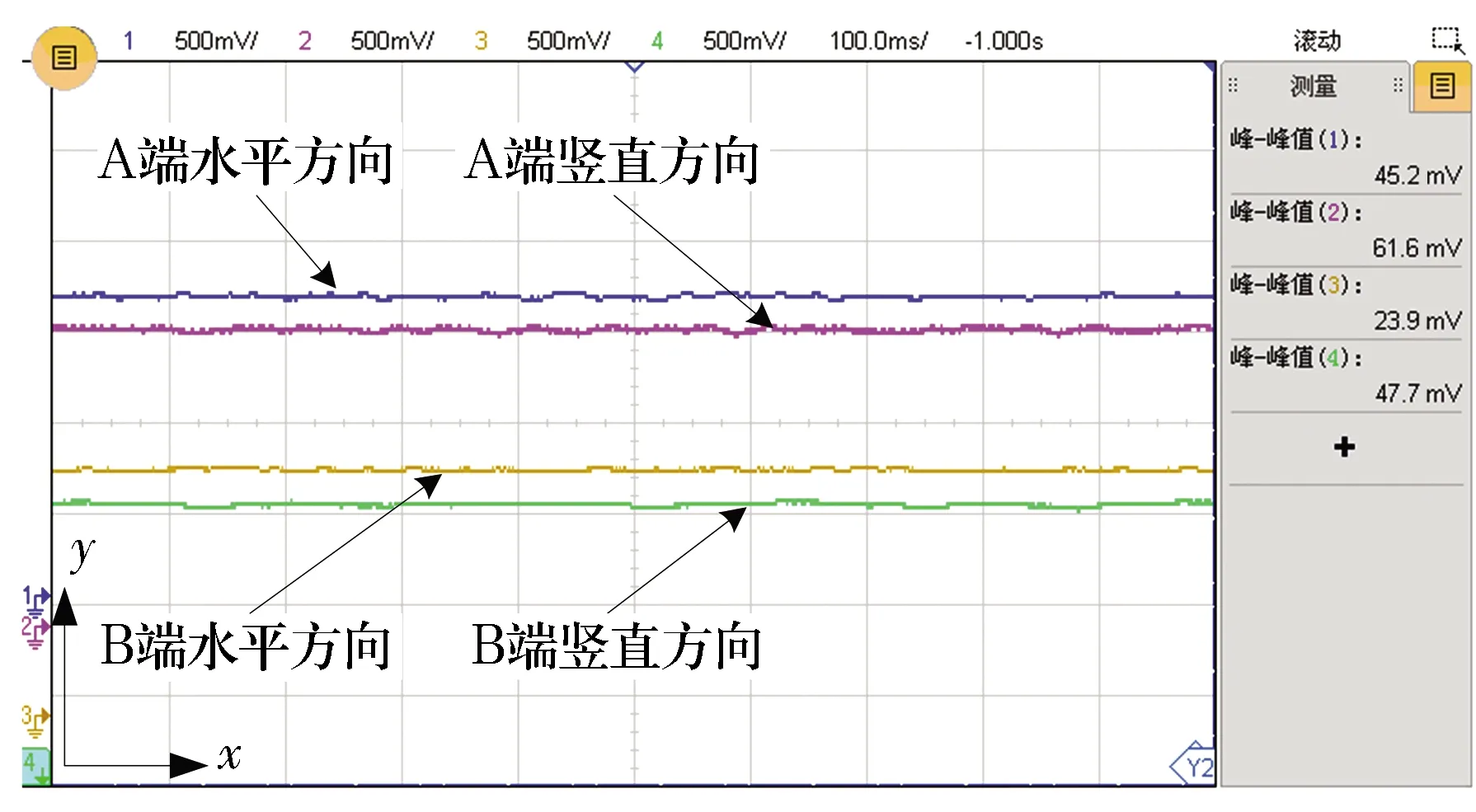
图4 PID控制的转子四自由度位移曲线Fig.4 Four-DOF displacement curve of rotor under PID control
2 模型辨识
2.1 辨识原理
为准确获取磁悬浮轴承系统的模型,在此采用频域辨识方法,精确获取系统的频率特性。根据线性系统理论,对于线性定常系统,若系统输入为一系列不同频率的谐波信号,则系统输出也是一系列对应频率的谐波信号,只是幅值和相位发生了变化。系统输出与输入的比值即为系统的频率特性。
频域辨识原理框图如图5所示,在闭环系统的位移参考端注入一系列谐波信号A0sin(ωt),分别采集辨识对象的输入信号S1和输出信号S2。对信号S1,S2进行离散傅里叶变换,两者的比值即为辨识对象的频率特性,将其表示成幅值与相位的形式,即
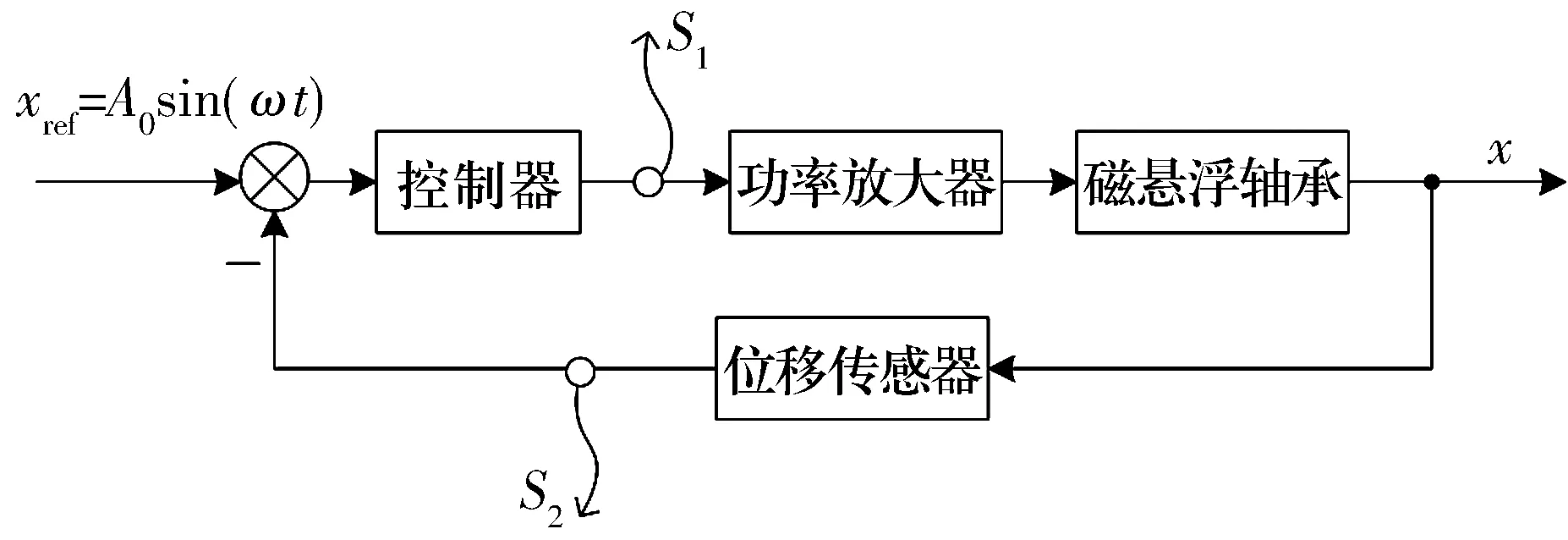
图5 频域辨识原理框图Fig.5 Principle block diagram of frequency domain identification
(4)
式中:|G(iω)|为辨识对象的幅值;φ(ω)为辨识对象的相位;i为虚数单位;ω为角频率。
根据幅值与相位,即可绘制出系统的伯德图。谐波信号幅值A0应适当选取,幅值太大易引起系统高频失稳,太小则不易区分干扰信号而引入误差,通常取转子最大运动间隙的5%~10%。考虑到闭环系统的带宽,谐波信号频率取600 Hz内的一系列频率,且这些频率按照一定的倍率变化,以便数据在伯德图上呈等距变化。辨识的对象除了磁悬浮轴承外,还包括功率放大器和位移传感器。
2.2 辨识结果
对图1和图3所示磁悬浮轴承系统的4个自由度做频域辨识,辨识结果如图6所示。由图6可知:
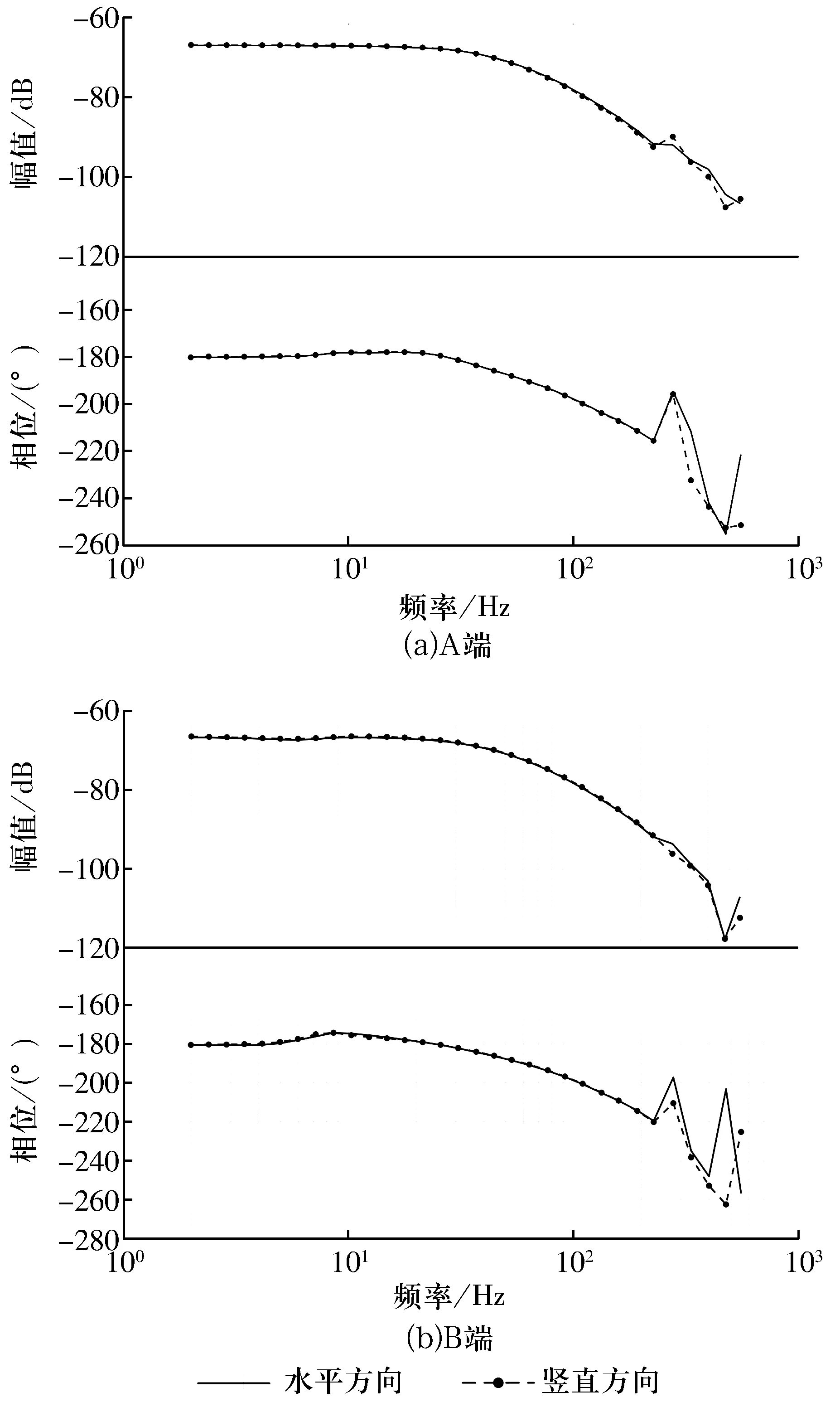
图6 磁悬浮轴承伯德图Fig.6 Bode plots of active magnetic bearing
1)同一端磁悬浮轴承水平方向与竖直方向的频率特性接近,在高频段有较小的误差。
2)两端磁悬浮轴承的频率特性具有相似性。以A端磁悬浮轴承为例,随频率增大,系统频率特性呈光滑变化,但在200 Hz以上的某些频率点,数据出现跳变,这是因为这些频率点与转子的某些固有频率重合,转子发生了谐振,导致采集的时域数据有较大的误差。
3)系统幅频曲线在低频时基本保持不变,反映了系统的直流增益,但随频率增大,幅频曲线逐渐衰减。相频曲线在低频时基本上保持不变,表明系统相位滞后180°,为二阶系统的特性,但随频率增大,相位滞后持续增加,在高频段相位滞后接近270°,呈三阶系统的特性。
2.3 模型拟合与分析
得到辨识对象的频率特性后,需对数据进行拟合,得到系统的传递函数。关于传递函数的拟合方法,文献[15-17]都做了详细介绍,文献[17]中提出的拟合方法专门针对磁悬浮轴承,在此采用文献[17]的拟合方法。
考虑到磁悬浮轴承理论模型为二阶模型,首先用二阶模型对频率数据进行拟合,其传递函数为
(5)
式中:b0,b1,b2为模型系数。
因为两端磁悬浮轴承的频率特性具有相似性,只给出A端磁悬浮轴承的拟合曲线,如图7所示,由图可知:在低频段,二阶模型能较好地描述系统的实际特性,但在高频段,二阶模型相位趋近于-180°,与实际系统的相位变化有较大的误差。4个自由度的二阶模型拟合结果见表1。
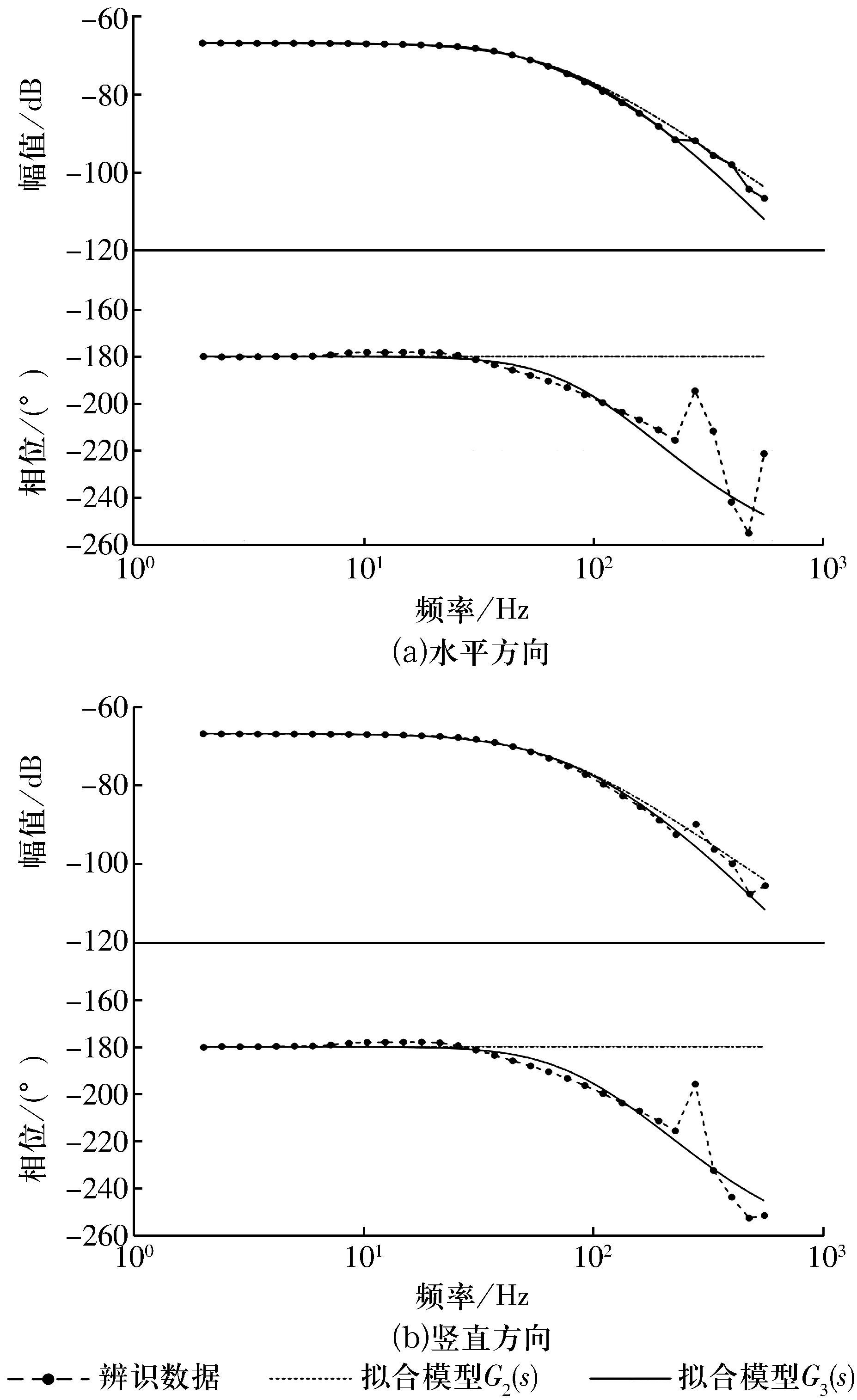
图7 A端磁悬浮轴承辨识数据拟合结果Fig.7 Fitting results of identification data of A end active magnetic bearing
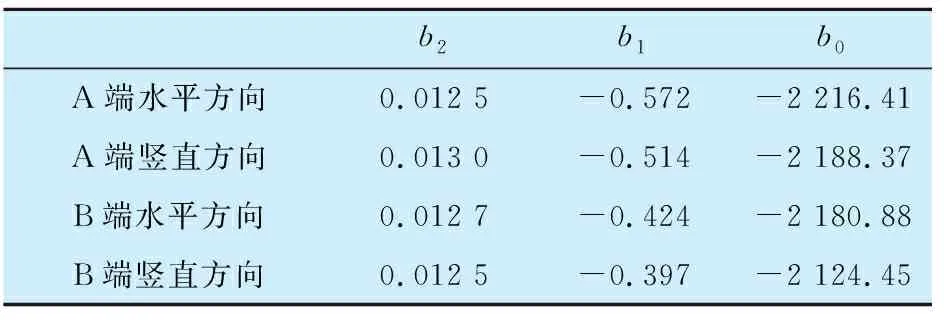
表1 二阶模型拟合结果Tab.1 Fitting result of second-order model
考虑到实际系统的相位滞后更接近三阶系统,因此也采用三阶模型对辨识数据进行拟合,三阶拟合模型的结构为
(6)
式中:b0,b1,b2,b3为模型系数。
拟合曲线如图7所示,相比于二阶模型,三阶模型在整个频率段与实际系统都有较好的吻合,能更好地描述系统的实际特性,拟合结果见表2。
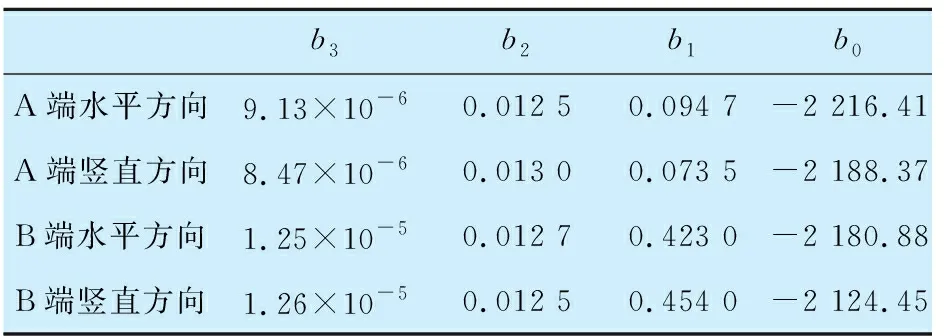
表2 三阶模型拟合结果Tab.2 Fitting result of third-order model
三阶模型的辨识对象除了磁悬浮轴承本身,还包括了功率放大器以及位移传感器,而理论建模通常不考虑后两者的影响。
试验装置中用到的位移传感器为电涡流位移传感器,通常表示为一个具有固定增益的一阶惯性环节,但其带宽为5 kHz,远远大于磁悬浮轴承位移控制闭环的带宽,在闭环系统的带宽范围内其数学模型可表示为一个固定常数,即
Gs(s)=Ks,
(7)
式中:Ks为传感器增益。
试验装置中磁悬浮轴承控制硬件的功率放大器为开关型功率放大器,其带宽有限,数学模型可以表示为一个具有固定增益的一阶惯性环节,即
(8)
式中:Ka为功率放大器的增益;τa为惯性环节的时间常数。
如图5所示,根据传递函数运算法则,由磁悬浮轴承、功率放大器和位移传感器三部分构成的系统开环传递函数为
(9)
由此得到的模型正好是一个三阶模型。理论建模时,若功率放大器和位移传感器的带宽有限,则应考虑这两者的动态特性,特别是功率放大器的滞后影响。开关型功率放大器的滞后作用与开关器件的性能有关,随频率增大,其滞后的影响也变得明显。
3 基于辨识模型的控制器设计
在三阶模型的基础上,重新设计控制器。根据控制理论,为实现闭环极点的任意配置,至少需要一个二阶控制器。为消除静态误差,控制器中再添加上积分作用,设计的控制器传递函数为
(10)
式中:A0,A1,B0,B1,B2,C0为控制器参数。
构成的闭环控制框图如图8所示。
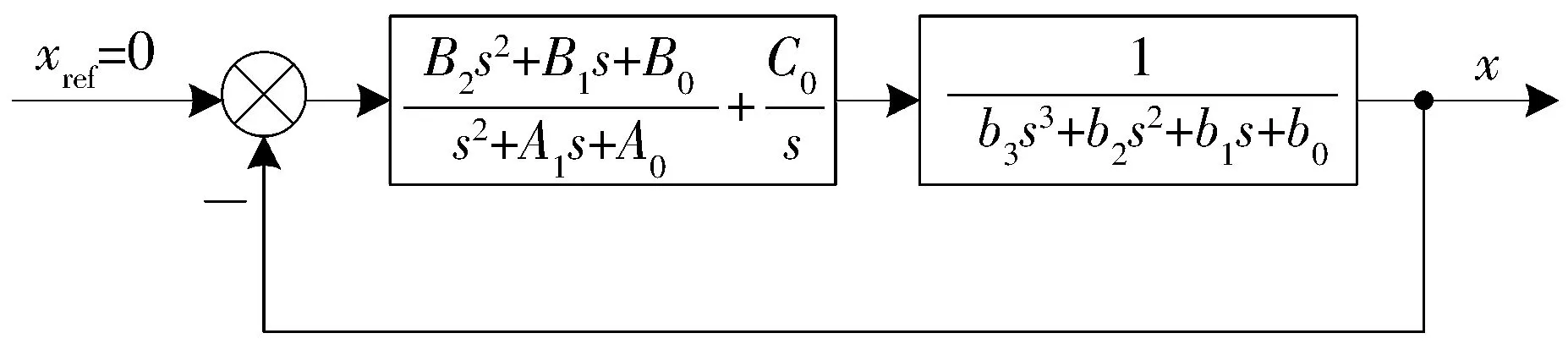
图8 闭环控制框图Fig.8 Block diagram of closed-loop control
控制器参数通过极点配置法确定。将闭环系统的极点配置在左半平面的相同位置(-r,0)处,为六重极点,得到控制器参数、模型参数与极点的关系为
(11)
(11)式形式上并非独立,后面的计算依赖前面的计算结果,这样有利于编程。通常闭环极点取磁悬浮轴承开环极点的1~3倍[18],在此取r=160π。
设计了4个控制器对4个自由度进行分散控制。控制器离散化后用于磁悬浮轴承系统的控制,同样实现了转子4个自由度的稳定悬浮,转子的稳定悬浮曲线通过示波器显示,如图9所示(x轴为时间,每格表示200 ms,y轴为位移,每格表示500 mV)。
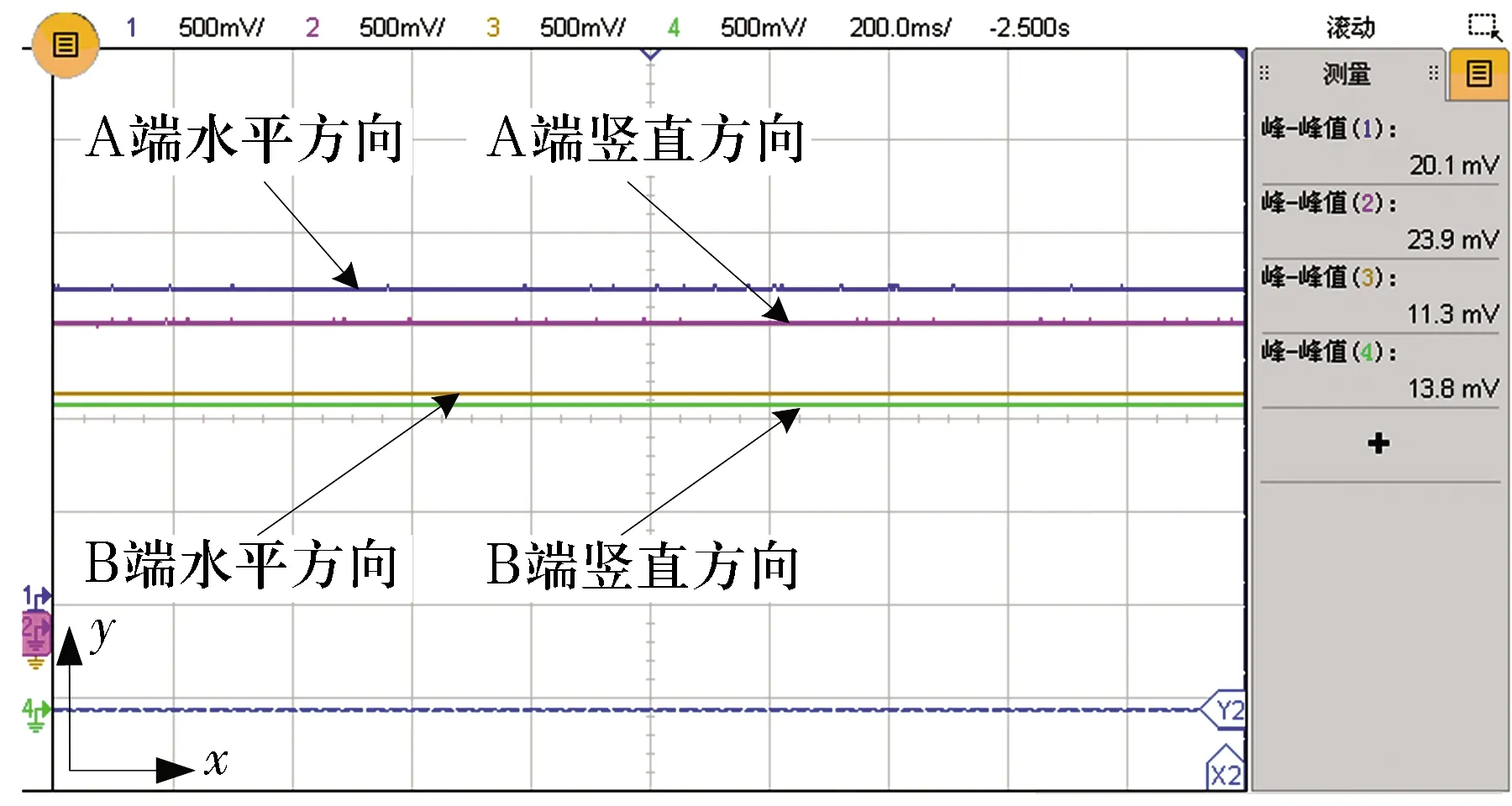
图9 基于辨识模型控制的转子四自由度位移曲线Fig.9 Four-DOF displacement curve of rotor based on identification model control
与图3所示的PID控制性能相比,基于辨识模型的控制精度有了很大提升,位移波动明显减小。将图4和图9的曲线波动峰值电压和对应的实际位移波动量对比,结果见表3。由表3可知:PID控制下转子稳态悬浮的最大位移波动量为14.67 μm,而基于辨识模型设计的控制器的稳态悬浮最大位移波动量为5.67 μm,减小了约60%,悬浮控制的稳态性能提高。实际调试过程也表明PID控制器的调试时间较长,控制器参数根据实际效果也做了多次改进,而基于辨识模型的控制器调试时间较短,且控制参数改动较小。
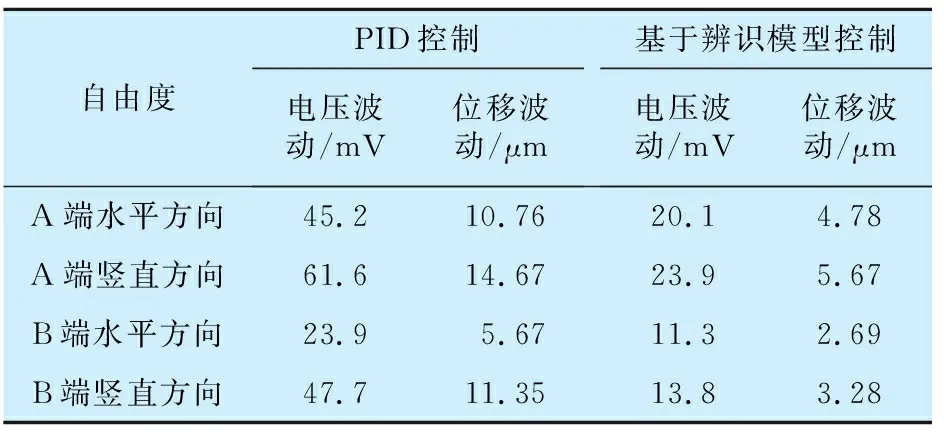
表3 转子四自由度稳态悬浮位移波动量Tab.3 Displacement fluctuation of four-DOF rotor under stable suspension
由此说明,模型辨识得到了精确的系统模型,而基于精确模型设计的控制器在缩短调试时间以及提升稳态控制性能上,均比基于理论模型设计的控制器有较大的优势。
4 结论
采用频域辨识法对四自由度磁悬浮轴承系统进行模型辨识,得到了精确的系统模型。基于精确模型设计了二阶控制器,实现了磁悬浮轴承四自由度的稳定悬浮控制。得出以下结论:
1)二阶理论模型的相位在中高频段不能准确描述四自由度磁悬浮轴承系统的频率特性,实际对象更接近三阶系统。
2)为提高模型精度,理论建模有必要考虑功率放大器和位移传感器的影响。
3)基于模型设计的控制器性能依赖于模型的准确性,提高系统模型的精度,可以提高控制器的控制性能。基于精确辨识模型设计的控制器比基于理论模型设计的控制器更具优势。
