基于灰色理论的铁路交通一般事故数据预测模型

胡哨刚，孔祥芳，旷利平，冯 博

(湖南高速铁路职业技术学院，湖南 衡阳 421000)

铁路交通事故按事故等级由大到小可分为特别重大事故、重大事故、较大事故、一般事故4类[1]。近年来，在铁路运输过程中一些重大灾难性事故，如“7·23”甬温线特别重大交通事故[2]虽已趋于成功避免发生，但其他造成轻微损失或人员伤亡的铁路一般事故仍然时有发生，并成为当前的主要类型铁路交通事故[3-7]，因此，在铁路行车安全管理[8]过程中，必须重视对铁路交通一般类事故的预测及研判。铁路交通事故的预测方法主要分为微观预测[9-10]与宏观预测[11-12]两种。微观预测以事故发生的风险因素作为因变量，探讨因变量与目标变量的关系，如贝叶斯法[13]、回归分析法、马尔科夫法、神经网络预测法等。微观预测中的回归分析预测[14]是以回归方程作为预测模型，根据自变量在预测期的数量变化情况来预测因变量的数量变化，但由于导致铁路交通事故的因素繁多，因此，无法据此建立准确的回归方程。李洪等[15]利用马尔科夫模型进行铁路事故预测，该方法操作简单，但预测范围有限且精度不足；白彦龙等[16]基于BP神经网络对2019-2020年煤矿事故数量进行预测，结果显示预测模型精度较高，但BP神经网络法对隐藏节点层的感知器不能解释，有待进一步研究。宏观预测趋向于事故的趋势预测[17-18]，如时间序列法、灰色预测法等，时间序列预测法分为加权时序平均数法、移动平均法和指数平滑法等。孟祥海等[19]运用时间序列预测法以我国1991—2015年道路交通事故死亡人数为研究对象，对2016年我国道路交通事故死亡人数进行预测，时间序列预测法的缺点在于不同时间模型的预测结果偏差较大；Talebnejad等[20]运用灰色理论对Fars省的道路交通事故进行预测，验证了模型的可行性。灰色系统[21-22]是既包含已知信息也包含未知信息的不确定系统，有其独特实用之处。囿于目前我国铁路各局集团较少对外披露详细事故报告情况，因此，铁路行车安全系统本身是一个部分信息未知的灰色系统，使用其他方法较难获取完整的事故致因信息，并据此建立可靠模型。而灰色预测Gery Model (1,1)模型的优点在于对样本量要求较小，适合短期预测，且对导致事故发生的因素收集不做要求，计算相对简单，其预测结果与事物发展趋势及定性分析结论接近。

1 建立GM(1,1)模型

文中拟选取2015—2019年事故数据建立GM(1,1)模型，将模型模拟获得的2015—2019年数据与原始数据进行比较，从灰色关联度、后验差比值、小误差概率等方面验证模型的精度值，并对照精度等级检验模型是否可行。如可行，则进行2020—2022年事故数据预测；如不可行，则利用残差对模型进行必要修正。具体步骤如下。

步骤1 数据处理

将原始数列记为：X(0)(k)={x(0)(1),x(0)(2),x(0)(3),x(0)(4)，…，x(0)(n)}，k=1,2,3,4,…,n，即原始序列第n时刻的原始数据。

为弱化原始数列的随机性，对原始数列进行一次累加,即(1-AGO),可得

(1)

得一次累加数列：X(1)(k)={x(1)(1),x(1)(2),x(1)(3),x(1)(4)，…，x(1)(n)}，k=1,2,3,4,…,n。

步骤2 数列检验

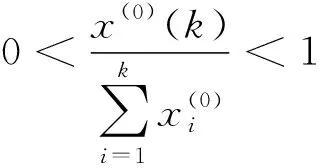
步骤3 构建矩阵B和向量Y

对X(1)(k)做紧邻值生成数列

x(1)(k))},k=2,3,…,n

(2)

构建矩阵B和向量Y为

步骤4 确定模型参数a、b

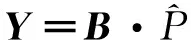
(3)

通过最小二乘法估计参数得

(4)

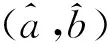
步骤5 还原预测数列

代入微分方程，得离散时间响应函数为

k=1,2,…，n

(5)

则预测值为

(6)

步骤6 模型检验

计算残差得

Q(k)={q1,q2,…,qn},k=1,2,3,4,…,n

(7)

相对误差为

(8)

平均相对误差为

(9)

2)后验差检验。设X(0)及Q(k)的方差分别为S1，S2，则

(10)

(11)

其中

(12)

计算后验差比

C=S2/S1

(13)

计算小误差概率

(14)

3)灰色关联度检验。灰色关联度是指两个数列在几何形状及变化趋势上的接近程度，接近程度越大，关联度越大，可用式(15)进行灰色关联度计算

(15)

式(15)中

(16)

(17)

对于预测模型可参照表1进行精度等级检验，观察模型是否可行。如精度一般，还需利用残差对模型进行修正。

表1 精度检验等级参照

2 算例分析

2.1 数据来源及选取

本文选取的数据主要来源于国家铁路集团公司官网及下属18个路局的季度事故统计文电，具体如表2所示。

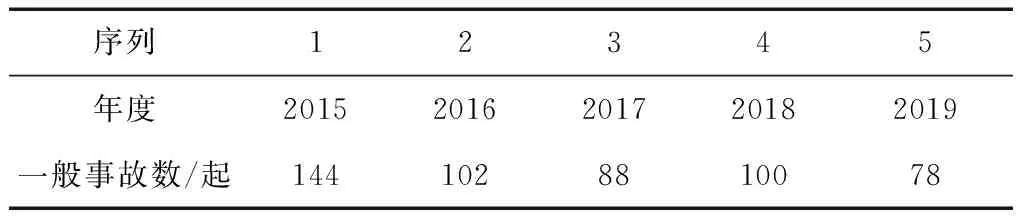
表2 2015—2019年全路一般事故数统计

将表2数据转化成散点图，如图1所示。

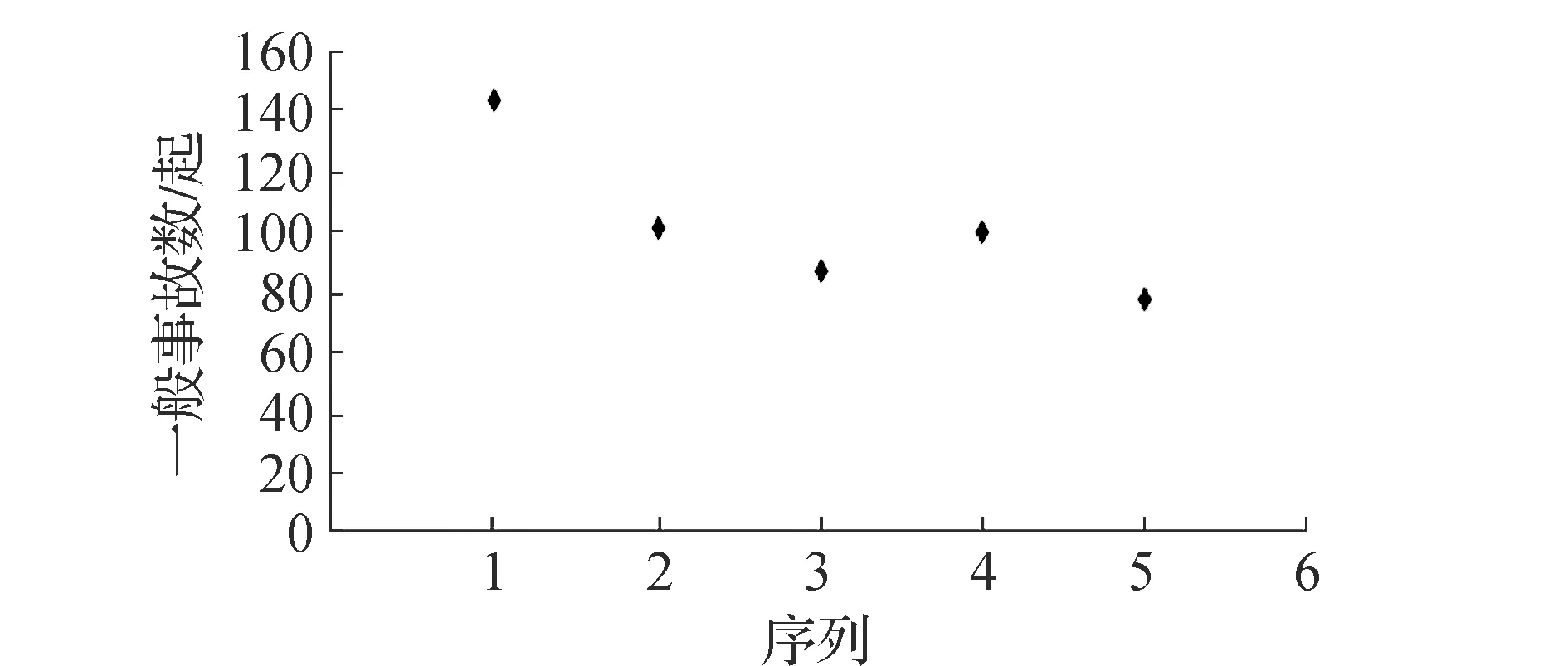
图1 全路一般事故数分布散点

2015—2019年全路每年铁路行车事故总数分别为144、 102、 88、100、78起，从图1可以初步看出，全路每年事故发生数整体呈下降趋势，且具有指数分布特征。

2.2 数据处理

将表2中的行车事故数据记为X(0)(k)={x(0)(1),x(0)(2),x(0)(3),x(0)(4),x(0)(5)}=[144,102,88,100,78]，作一次累加(1-AGO)，得X(1)(k)={x(1)(1),x(1)(2),x(1)(3),x(1)(4),x(1)(5)}=[144,246,334,434,512]。

2.3 数据检验

1)对原始数列X(0)(k)进行准光滑检验，当K>2时，88/246<0.5，准光滑条件满足。

2)对累加数列进行准指数律检验

当K>2时，334/246=1.36<1.5，数列X(1)(k)自K>2后，准指数分布满足，故可对累加数列X(1)(k)建立GM(1,1)模型。

2.4 构建矩阵B和向量Y

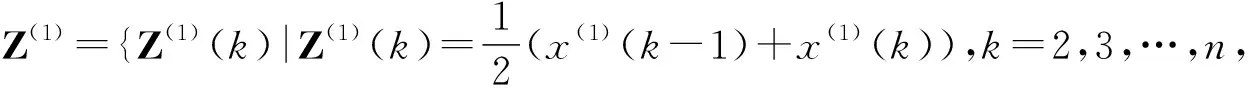
构建矩阵B和向量Y

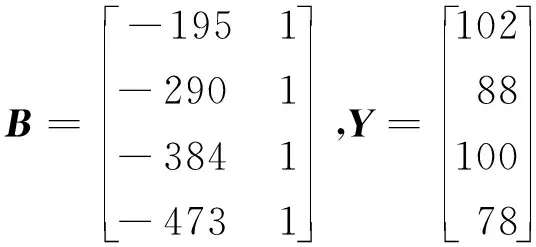
2.5 确定模型参数a、b

用MATLAB R2018a运算，得

2.6 还原预测数列

代入微分方程，可得离散时间响应函数为

还原预测数列为

107.685 5e-0.064 1k

Gery Model (1,1)预测数列为

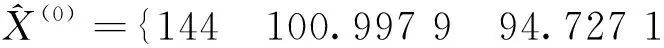
88.845 6 83.329 3}

2.7 结果分析

本文利用MATLAB R2018a编制了计算及绘图程序，运行程序得到2015—2019年铁路行车一般事故数据模拟值为{144.000 0 101.001 1 94.731 7 88.851 4 83.336 1},由于四舍五入原因，MATLAB R2018a计算与人工计算预测数据{144.000 0 100.997 9 94.727 1 88.845 6 83.329 3}在小数点后4位存在一些不同，属正常范围误差。绘图程序运行结果如图2所示。

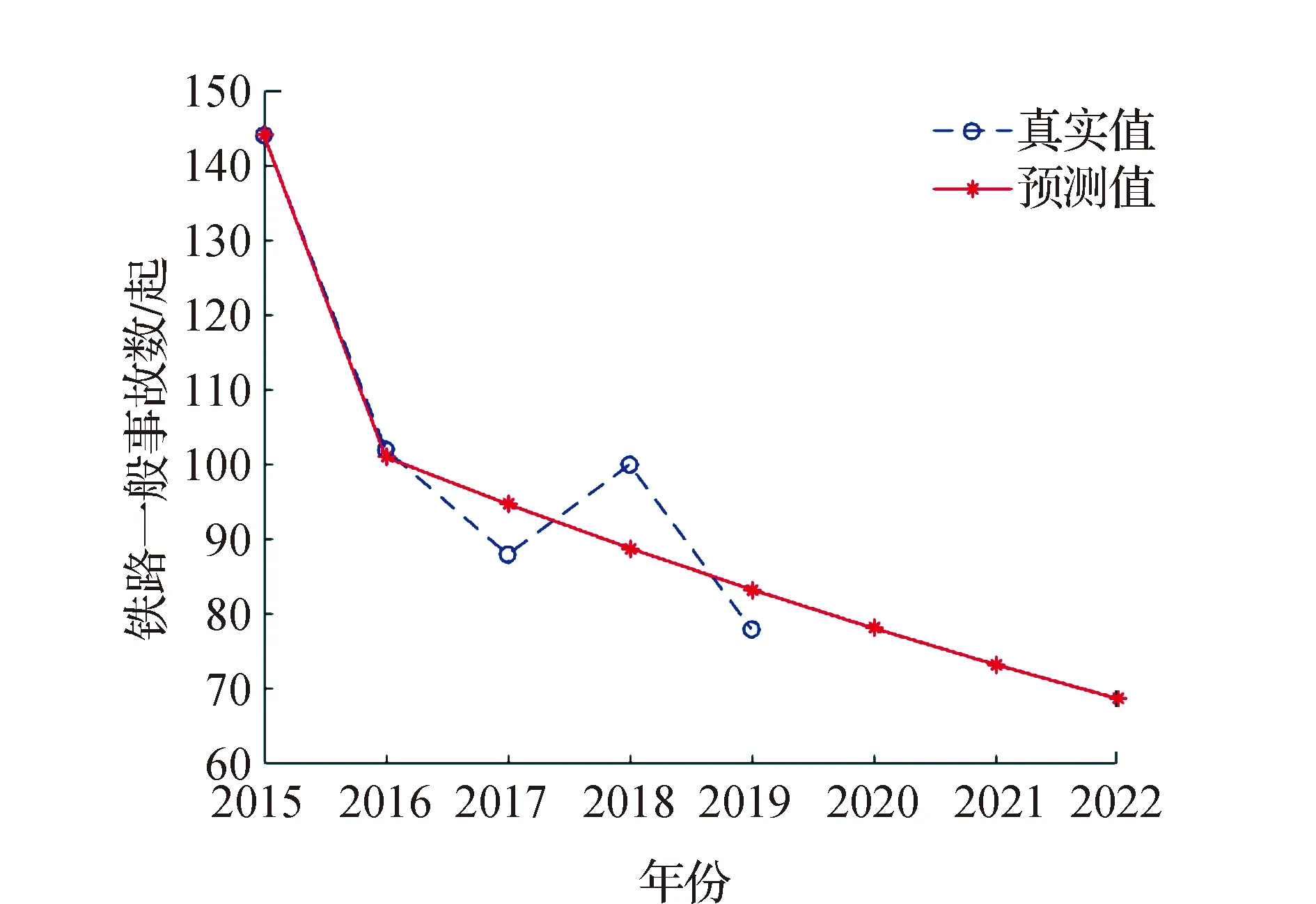
图2 基于2015—2019年数据对未来3年的预测

2.8 模型检验

2.8.1 残差检验

按Gery Model (1,1)得:

2)原始数列X(0)={x(0)(1),x(0)(2),x(0)(3),x(0)(4),x(0)(5)}={144 102 88 100 78}；

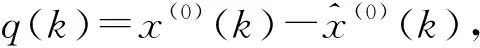
-6.721 0 11.154 4 -5.329 3};

4)相对误差ε(k)={0 0.006 0.066 0.126 0.068};

具体计算结果如表3所示。

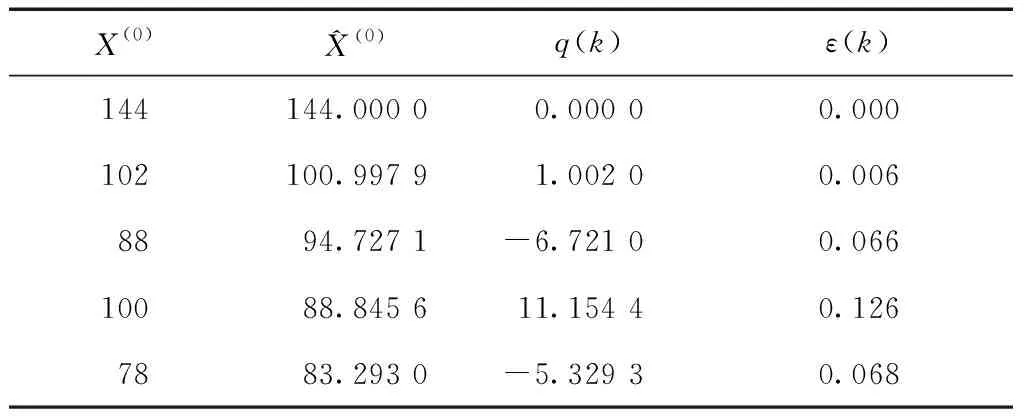
表3 GM(1,1)模型残差检验

2.8.2 后验差检验

令数列X(0)和Q(k)的方差分别为S1，S2。运用MATLAB R2018a对式(10)、式(11)进行方差求解，在MATLAB R2018a中输入

Var1=sum(x(1,:)-mean(x)).∧2)/length(x)

Var2=sum(q(1,:)-mean(q)).∧2)/length(q)

得

则后验差比值：C=S2/S1=0.339 1。

代入式(14)计算小误差概率为

2.8.3 灰色关联度检验

对式(15)进行灰色关联度计算，结果为：ro1=1-0.121 3=0.878 7。对残差检验、后验差检验及灰色关联度检验进行列表汇总，如表4所示。

表4 模型检验值

对照表1，后验差比值C=0.339 1<0.350 0、小误差概率P=1>0.95，精度等级均为一级，灰色关联度精度0.80

2.9 模型预测

由于建立的模型精度较高，所以可根据模型对2020—2022年的铁路交通一般类事故发生数进行预测，结果如表5所示。

表5 全路2020—2022年铁路行车一般事故发生数预测

3 结 语

1)通过对各类预测方法的比较，最终选择对样本量要求小、计算量不大的灰色系统理论中的GM(1,1)模型进行研究。基于2015—2019年中国国家铁路集团公司下辖18个路局集团的全年铁路行车一般事故发生数数据，对全路2020—2022年行车一般类事故发生总数进行预测。研究结果显示模型的精度等级较高，2020—2022年事故发生数呈下降趋势，全国铁路行车安全形势有所好转。

2)受新冠疫情影响，全路开行列车对数减少，也是铁路交通事故数量降低的重要原因。各路局仍不能放松警惕，日常安全管理过程中应及时对近年发生的典型事故案例进行剖析，从风险管理、职工教育及技术控制3个方向进行防控，在安全风险研判、作业过程控制、管理人员履职、新职人员管控、事故教训吸取、风险问题闭环管理、风险管控评价机制、信息上报制度、技防设备运用、岗位互控考核管理、安全分析中心作用、职工技能培训等12个方面加强重点卡控，确保铁路行车安全。