基于大数据分析的多维公路货运价格预测问题研究

陈 俐，方叶祥，甘平，樊树海

(南京工业大学 经济与管理学院，江苏 南京 211816)

随着我国经济的发展，国内现代物流运输行业也呈现出快速发展趋势。公路货运由于具有快速、灵活的特点，目前已成为国内综合运输体系中规模最大和最重要的货运方式[1-2]。在互联网技术快速发展的背景下，我国涌现出许多公路货运平台，在货运平台中，运价是保证货主与承运人利益的关键[3-4]。公路货运价格受到多种因素影响，如货物类型、运输距离、油价等，这些影响因素中既有分类因素，也有数值因素，类型较复杂，尤其是受到油价等随时间动态变化因素影响而无法精确预测，一直以来困扰着货物运输行业。

影响公路货运价格的形成因素较多，其中主要的影响因素有运输成本、货运供求关系、货运市场结构、国家经济政策及各种运输方式之间的竞争[5-8]。近年来，相关学者对公路货运价格的相关问题进行了一系列研究。Joseph等[9]回顾了货运预测模型及数据和模型开发方面的最新进展和需求；汤银英等[10]运用马尔可夫模型，并根据转移状态为离散型随机变量这一特征，利用状态区间中值期望对预测结果进行了修正，最后建立了改进型灰色马尔可夫模型对公路货运价格进行预测；冯芬玲等[11]基于博弈理论研究分析铁路和公路货运的竞争行为，并建立了铁路货运和公路货运的Hoteling模型，分析了运输价格和服务质量之间的关系及其对竞争的影响；刘世超[12]在考虑了经营利润和市场竞争结果的社会福利最大化情况下，运用双层规划方法确定公路货运价格；方启稳[13]选取了距离、承运商、国家经济发展水平等多个因素，分别建立了多元回归模型、BP神经网络模型与GA-BP模型，通过使用测试样本对3个模型进行测试，发现GA-BP模型对样本的拟合效果要优于其他2个模型；马银波[14]运用时间序列分析方法实证分析了中国公路货运行业运价与需求之间的动态关系,包括长期趋势、季节变动及货运需求与运价之间的相互作用关系；Kavussanos等[15]研究了货运期货市场中期货与现货价格之间的因果关系，认为当期货价格中包含的信息以VECM形式表示时，可以对现货价格进行更准确的预测，而且要提前数步。

公路货运价格受到多种因素的综合影响，然而现有的预测方法存在着未考虑地理信息因素、随时间变化影响因素的动态特征及预测准确度有待提高等问题。尤其是随时间变化的影响因素，这也是造成公路货运价格出现季节性波动的主要原因[16]。因此，对众多影响因素进行正确处理，才能有效提高公路货运价格预测的合理性与准确性。

本文针对公路货运价格的预测问题，首先，将起点与终点的经纬度信息转变成地理信息编码，并从中提取出省份、城市信息，从而对货运订单实现了跨区域分类；然后，利用时间序列预测模型对油价及货运周转量的动态特征进行预测；最后，建立了时间序列预测与BP神经网络的组合模型，对公路货运价格进行预测。

1 货运价格预测模型建立

1.1 问题描述与分析

影响公路货运定价的因素众多，以“中储智慧运输物流电子商务平台”提供的货运订单信息为例，其订单信息主要包括日期、一级品类、详细品类、订单类型、交易类型、货值、起运地经度、起运地纬度、目的地经度、目的地纬度、运距、车型、车长和运价，共14个项目。从中可以看出运价的确定会受到多个因素的共同影响，在众多影响因素中，既有定性的分类数据，也有定量数据，特征维度大，数据类型复杂，因此，影响因素的选取和处理以及预测方法的选择都将对构建的价格预测模型效果产生较大影响。

1.2 数据分析与特征处理

虽然货运平台提供的订单由14个项目构成，但并不是每一个项目都对运价有显著影响，因此需要对每一个项目进行分析，去除冗余特征。

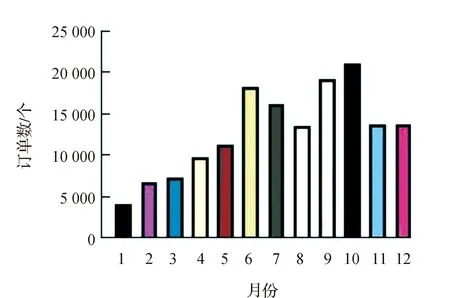
数据来源：中储智慧运输物流电子商务平台图1 订单数量统计

首先对订单按“日期”信息进行分析，统计出每个月订单数量，统计结果如图1所示。从图1可以看出每月货运订单的数量变化明显，且下半年的订单数量要明显高于上半年，6月、7月、9月与10月为该平台货运的高峰时期，考虑到供需与价格的关系，订单的履行日期会对运价产生一定影响，因此，需要选择订单信息外与时间相关特征，由于价格变化主要由需求量的周期变化引起，所以选取了公路货运周转量作为特征，同时考虑到公路运输的主要成本来源于燃油，燃油价格的变化势必会对运价造成影响，在长距离运输中影响更为显著。综合以上观点，将公路货运周转量及燃油价格作为时间特征上的两个维度，用于反映“日期”对运价的影响。

再对一级品类和详细品类进行分析，先对订单按一级品类进行归类统计，如图2所示，从中可以看出约72%的订单运输货物归属于品类1，品类2和品类3分别占11%和13%，而品类4只占4%。

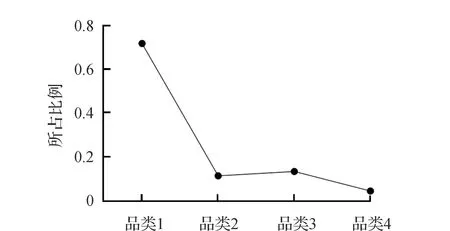
数据来源：中储智慧运输物流电子商务平台图2 品类占比

为进一步研究货物品类与运价之间的关系，按一级品类的不同对订单中的运价进行区间统计，统计结果如表1所示。可以看出不同品类货物运价的价格集中区间有所不同，品类2与其他品类相比较为特殊，其运价主要集中在100～300元/t，大于300元/t的订单占比也较多，其他3个品类在前3个价格区间的订单数量都呈现出递减趋势，但减少的幅度并不相同，差别较大。由于4种品类的运输价格变化有着较显著差别，因此，一级品类在运输价格预测中具有不可或缺的特征。

表1 运价区间统计(按品类) %

详细品类同样是对运输货物进行了分类，计算其与运输价格之间的Pearson相关系数，得到相关系数R为0.17，说明两者之间并没有显著相关性，所以不选择详细品类作为特征。

通过统计发现，约有98%的订单中“订单类型”项相同，约有96%的订单中“交易类型”项一致，说明“订单类型”与“交易类型”不能对订单进行有效区分，不适合作为预测模型特征。同时，在对货值与运价进行Pearson相关性分析后，发现其相关系数R仅为0.01，两者并不具备显著相关性，因此，也不适合用作运价预测。

订单中包含的空间信息主要由起点经纬度、终点经纬度以及运距构成，其中运距与运价的Pearson相关系数R为0.898，说明运距在运价的预测中不可忽视。起点与终点的经纬度信息可利用高德地图API接口转换成具体地址与地区编码，利用不同承运人在选择订单时对长途与短途的不同倾向性将货运订单分为3类：跨省运输，跨市运输和市内运输。统计发现，73%的货运订单属于跨省运输，占比最大，其次是跨市运输订单，占18%，市内运输订单最少，只占9%。如图3所示。

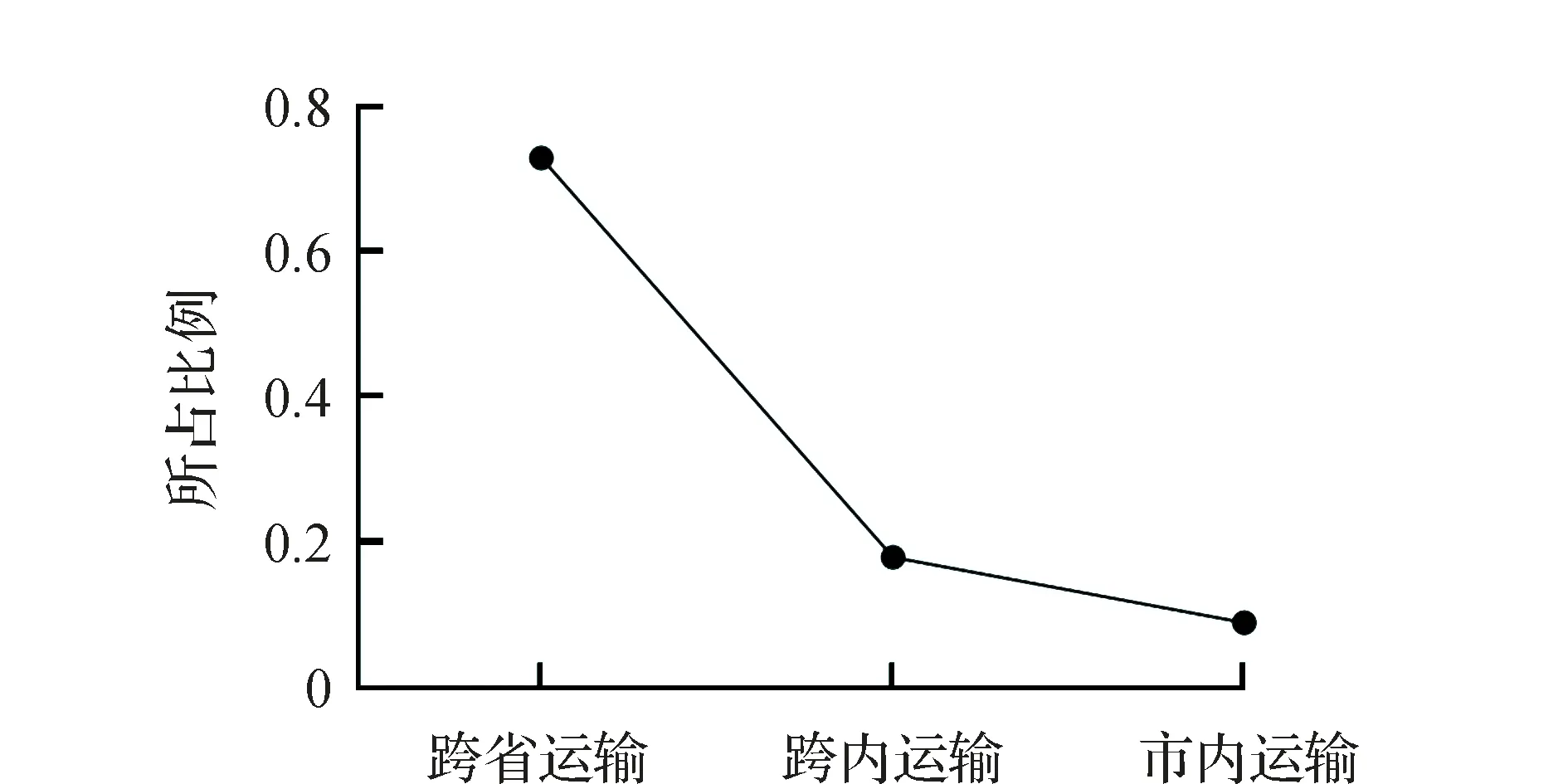
图3 跨区域订单占比

为进一步探究3种类型订单运价的不同，对其按类别进行价格区间统计，如表2所示。结果显示跨省运输的订单运价集中在100～200元/t，同时有约33%的跨省运输订单运价超过了200元/t，与另外两类订单产生了较为明显区别。跨市与市内运输订单运价大多小于100元/t，市内运输订单中只有3.56%的运输价格超过了100元/t。由于3种类型的订单运价有较为显著区别，因此，对货运订单进行跨省、跨市和市内运输分类能有效帮助确定运价，提高运价预测精度。

表2 跨区域分类运价区间统计 %

在公路运输中，运输车辆的不同也会对运价产生一定程度的影响，在订单信息中“车型”与“车长”都是描述运输车辆的信息，其中车型为分类数据、车长为定量数据，由于不同车型的车长信息区别较小，因此，选择车长作为描述运输车辆的特征用于预测运输价格。

数据来源：中储智慧运输物流电子商务平台

通过以上分析，将公路货运周转量与油价作为时间特征，一级品类、运距和车长作为可由订单直接获取的特征，运输跨区域情况作为空间特征，并将以上特征作为预测模型的输入内容。

1.3 时间特征预测

虽然该平台大多数订单是提前几天达成的，但仍存在着提前数星期、甚至1个月签订的订单，由于燃油价格以及货运季节的变化，若价格按照订单签订时的油价及货运季节情况确定，那么承运人在订单实际履行时所花费的成本可能会发生较大改变，从而导致货主或承运人的利益受损，因此，对于该类提前订单，需要对订单实际履行时的时间特征进行预测。

为捕捉、描述公路货运周转量与燃油价格的动态变化，使用时间序列分析研究过去的时间序列动态变化(见图4)，分析其中的变化规律，如长期趋势变动、季节变动、循环变动和不规则变动，从而依据数值变化规律预测未来数值趋势。由于公路货运周转量的变动季节性与规律性较强，所以使用了指数平滑法[17]对其进行分析；考虑到油价的变化较为复杂，规律性不易捕捉，因此选择了ARIMA模型[18-19]对油价变化进行分析预测。

1.3.1 公路货运周转量预测

从中国交通运输部网站获取了2013年1月至2017年6月的公路货运周转量数据作为基础数据，根据得到的数据做出时间序列图，如图4所示。从时间序列图可以看出，公路货运周转量具有明显的周期性与季节性特征，一月、二月的数据相较于其他月份比较低，并且在之后的月份中也会呈现出增长趋势。

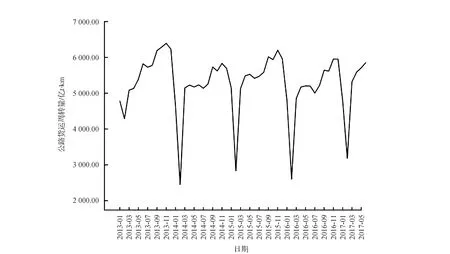
数据来源：中国交通部运输网站图4货运周转量时间序列

运用SPSS软件对数据进行季节性分解，在考虑季节因素的条件下建立指数平滑预测模型，对2017年7月12日的货运周转量数据进行预测，并与真实数据进行对比，模型的统计数据如表3所示，对比结果如表4所示。

表3 模型统计量

表4 预测数据对比分析

从表3和表4可以看出：得到的模型R2值为0.897，且Sig.值大于0.6，说明模型的拟合度较好、可信度较高；从预测值与实际值的对比情况看，最大偏差为3.08%，平均误差为1.40%，也说明了模型的可用性比较高。因此，用时间序列模型对货运周转量数据进行预测较为准确。

1.3.2 燃油价格预测

从中国国家统计局网站中获取了2014年1月至2017年6月的柴油价格数据作为基础数据，由于柴油价格波动性较大,且具有季节性特征，所以对数据进行了一般性差分与季节性差分，最终将柴油价格转变成为平稳序列，从而建立了ARIMA模型。经过多次实验发现ARIMA(2,1,2)(0,1,1)模型最优，模型的R2为0.741，正态化的BIC的值为12.080，说明模型的可信度较高。最终的预测值与实际值对比结果如表5所示，从表5可以看出预测的价格走势与实际一致，预测的最大偏差值为6.96%，平均偏差值为3.51%，模型的预测较为准确，但由于柴油价格受多种因素影响，波动性较大，因此，ARIMA模型适合于短期预测。

表5 油价预测值与实际值对比

数据来源：中国国家统计局

1.4 组合预测模型建立

1.4.1 BP神经网络

在选取的多个特征中，既存在线性的影响特征，也存在非线性的影响特征，因此选用了BP神经网络对其进行拟合。BP神经网络是一种按照误差反向传播算法训练的多层前馈神经网络，是目前应用较为广泛的神经网络[20-22]。典型的BP神经网络一般包括输入层、隐藏层和输出层，BP神经网络在进行学习和训练时主要考虑因素有隐含层数、隐含层神经元数、网络权值、期望误差和学习速率[23]。BP神经网络包含前向传播与反向传播两个过程。在前向传播过程中，根据输入层的输入经各层之间的权值计算，得到输出层的输出与误差，然后将误差进行反向传播，并更新各层之间的连接权值。

1.4.2 组合预测模型

为了对公路货运定价进行有效预测，建立时间序列预测与BP神经网络的组合模型，模型预测流程如图5所示。首先，将订单中的一级品类、运距、车长及起点、终点经纬度信息进行提取，并根据起点与终点的信息将订单划分成：跨省运输、跨市运输及市内运输；然后，根据订单实际履行日期判断其是否为提前订单，若为提前订单，则使用时间序列模型对订单实际履行时的油价及货运周转量进行预测，若不是提前订单，则直接使用当前的油价和货运周转量信息；最后，将得到的数据作为输入数据，利用BP神经网络对公路货运价格进行预测。

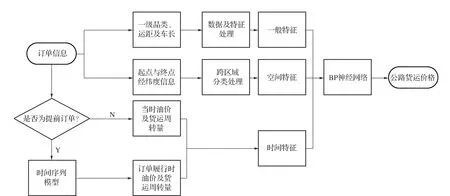
图5 模型预测流程

1.5 模型训练与检验

将“中储智运”平台提供的约16万条订单数据划分成训练样本及测试样本，采取随机抽取的方式从中选取12万条订单数据作为训练样本，并将剩余的4万条订单数据作为测试样本。

根据不考虑空间特征与时间特征、只考虑空间

特征不考虑时间特征、空间与时间都纳入考虑3种情况，建立3种预测模型，使用测试样本进行测试，并对模型的预测效果进行对比，使用均方根误差(RMSE)与平均绝对百分误差(MAPE)对模型的预测效果进行评价，均方根误差与平均绝对百分误差算式为

(1)

(2)

通过实验可得到3种情况下的模型预测误差情况，如表6所示。

表6 不同模型预测误差对比

从3个模型的评价指标来看，模型3的预测效果最好，模型1的效果最差。通过对比模型1和模型2的预测效果可以发现，在对货运价格进行预测时空间特征不可忽视，对订单信息中的空间信息进行恰当处理后，均方根误差减小了11.61，平均绝对百分误差减小了48.16%，预测效果有明显提高。将模型2与模型3进行对比，模型3的均方根误差比模型2减小了54.4，同时平均绝对百分误差也减小了37.6%，说明随时间变化的动态影响因素会对货运价格产生较大影响，在对货运价格进行预测时，必须考虑时间因素的动态变化。总体说，同时考虑了空间、时间特征的模型在测试样本上的预测效果表现更好，考虑到训练与测试样本数量较大，会存在较多的错误或特殊数据，最终模型3的预测误差可以接受。

2 运价预测试验分析

2.1 不同品类订单运输价格预测

为检验预测模型对不同品类订单运价的预测能力，随机选取4种品类各20条订单，并利用预测模型对其运价进行预测，预测结果如图6所示。从图6可以看出，不同品类订单的运输价格稍有差别，但多数订单的运输价格都低于200元/t，品类1、品类3与品类4的订单运价在0～200元的价格区间内分布较为密集，而品类4中约有40%的订单运价超过了200元/t，在各品类中占比最大。

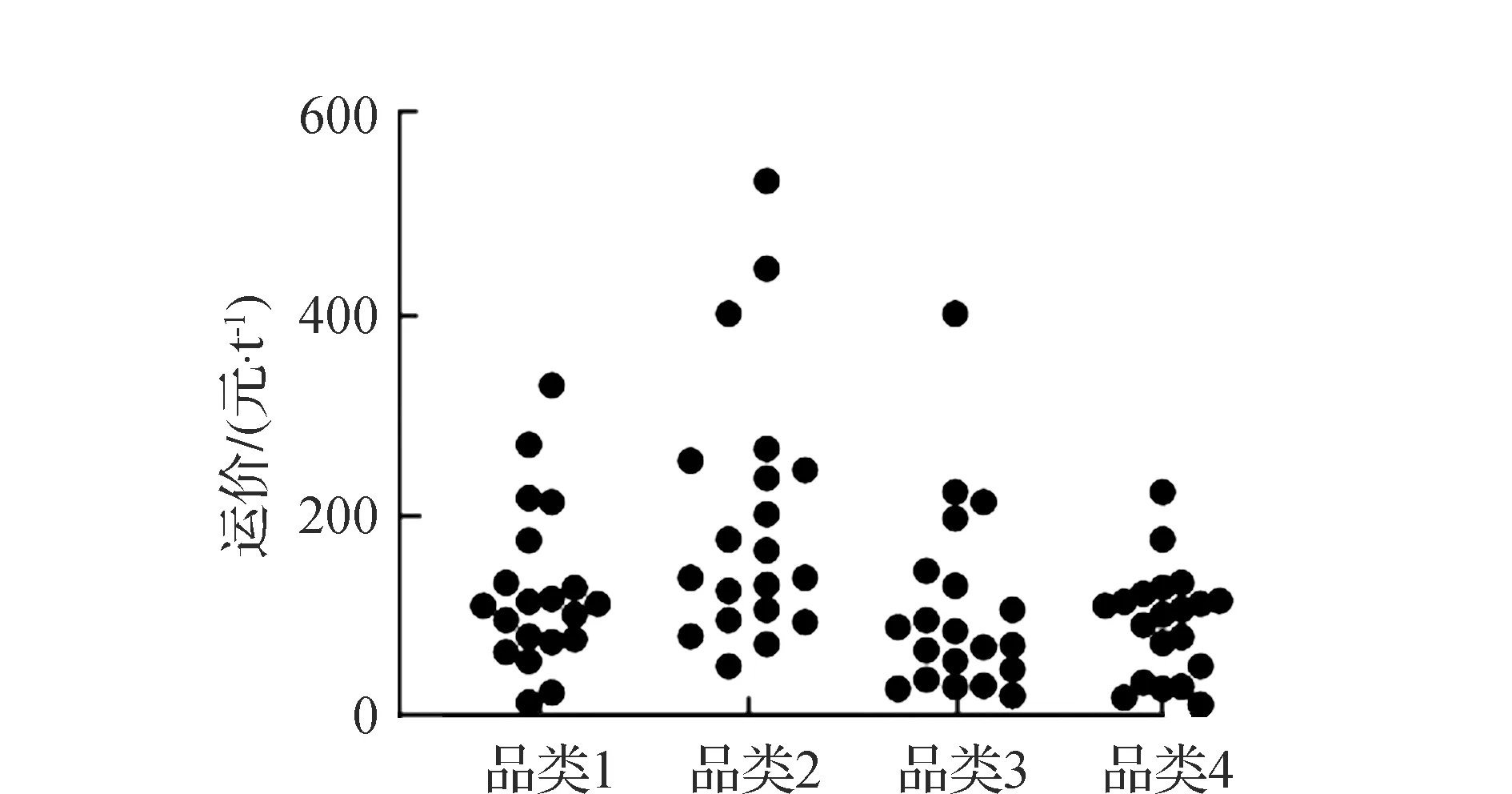
图6 不同品类订单预测运价分布

从该预测试验的结果来看，各品类的预测价格分布基本符合训练样本中的分布规律，说明建立的预测模型能够有效地对不同品类订单进行区分，并根据订单货物品类的不同对运输价格做出有针对性的预测。

2.2 跨区域运输价格预测

随机从各个品类的订单中抽取“跨省、跨市与市内运输”3类订单各20条，对各条订单的运输价格进行预测，在“跨省、跨市与市内运输”3种情况下，不同品类预测运价的分布情况如图7—图9所示，从预测结果来看，跨省运输均价最高、市内运输均价最低。在跨省运输中，各品类订单的运价变动幅度较大，在品类2与品类4中体现较为明显；在跨市运输中，各品类订单的运价较为集中，且运输均价呈现出递减趋势；而在市内运输中，各品类的货物运价都较低，预测运价均低于100元/t，尤其是品类4的订单预测运价均低于50元/t。

从跨区域运输价格预测试验结果看，3种运输情况下预测价格区别明显，且在相同运输情况下，不同的货物品类运价也呈现出不同的分布特点，说明“跨省、跨市与市内运输”3种运输情况的划分有效，且价格预测模型能够对3种不同情况进行区分，并根据品类的不同做出价格预测。各品类预测价格分布如图7—图9所示。

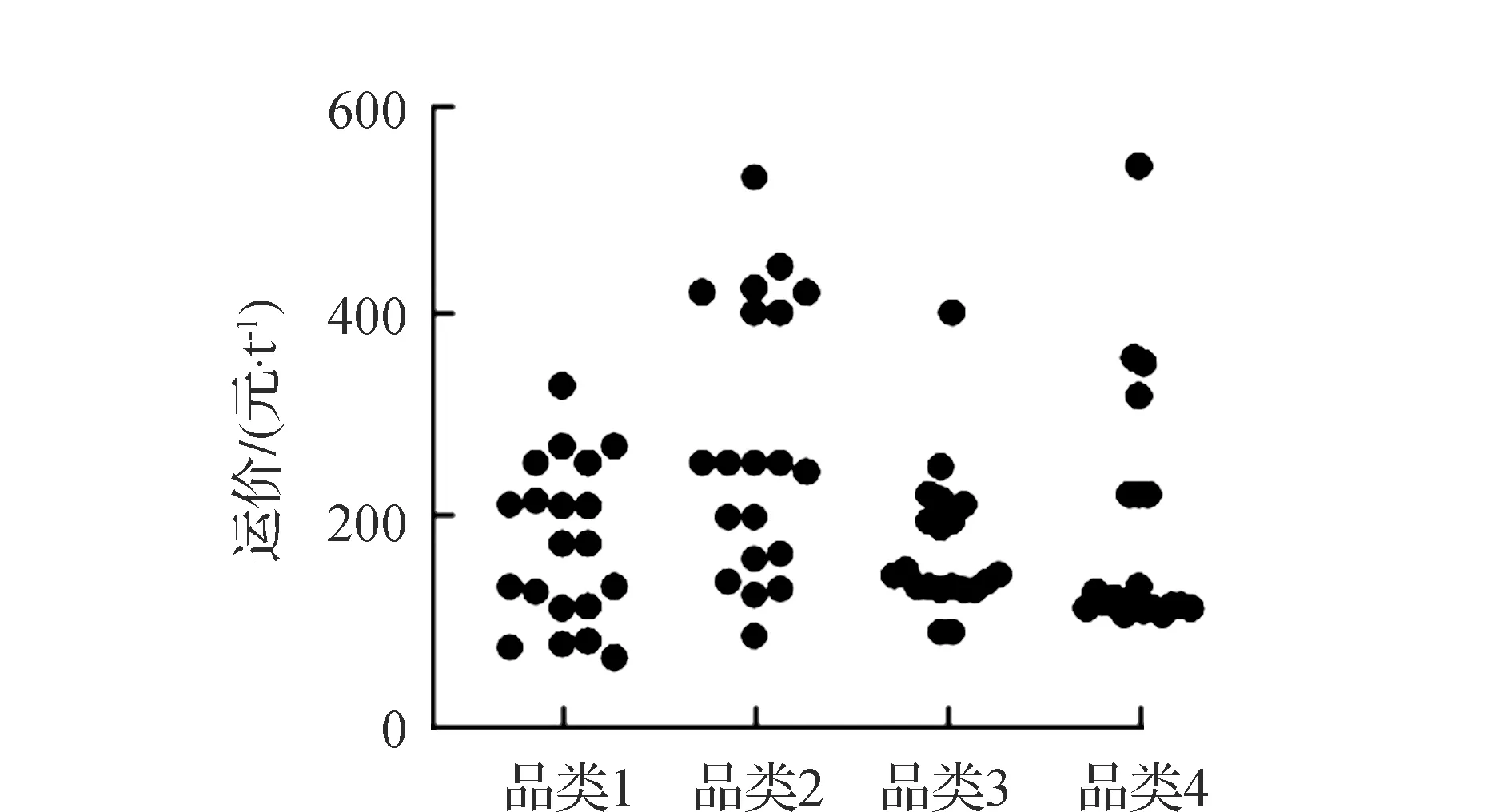
图7 各品类预测价格分布(跨省运输)

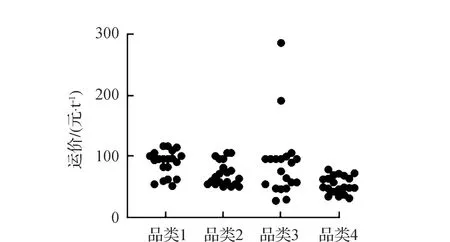
图8 各品类预测价格分布(跨市运输)

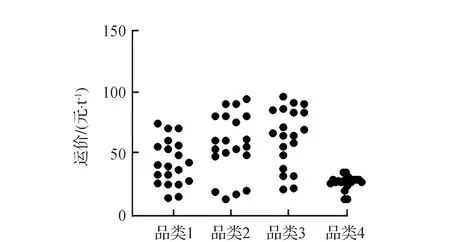
图9 各品类预测价格分布(市内运输)

3 结 语

本研究在考虑了公路货运订单中的空间特征及时间特征的动态变化情况下，建立了时间序列与BP神经网络的组合模型。首先，利用高德地图API接口将订单中起点、终点的经纬度数据转变成起点与终点的地理信息编码，进而对订单进行了跨区域分类；然后，提出了针对提前订单的时间特征预测方法，即利用指数平滑法和ARIMA模型对公路货运周转量及柴油价格的动态变化进行预测；接着，建立了时间序列与BP神经网络的组合预测模型，并使用“中储智运”的货运平台数据对组合模型进行测试，测试结果发现相较于只考虑订单中的一般特征模型，组合模型的平均绝对百分误差减小了85.76%。相对于考虑空间特征，不考虑时间特征的动态变化模型，组合模型的预测精度也提高了37.6%。最后，对运价预测模型进行了试验分析，结果显示预测模型能够有效地对不同品类订单及本文提出的“跨省、跨市与市内运输”订单进行区分，并给出有针对性的预测运价。总体说，本研究建立的组合模型可以有效地对公路货运价格进行预测，对公路货运市场的价格制定具有一定参考价值。