动态加载下HTPB 复合固体推进剂双轴压缩试验件设计

耿挺京，强洪夫，王哲君，王学仁，岳春国，王稼祥，周程哲2，

（1. 火箭军工程大学导弹工程学院，陕西 西安 710025；2. 西安航天化学动力有限公司，陕西 西安 710025）

1 引言

固体推进剂药柱是固体火箭发动机（Solid Rocket Motor，SRM）结构的重要组成部分，其结构完整性是保证动力系统可靠性工作的决定因素［1］。近年来，国内外在进行SRM 点火试车和导弹发射时，多次发生因推进剂药柱结构完整性破坏而造成的发动机解体、爆炸等事故，造成了无法挽回的重大人员及财产损失［2-3］。在SRM 点火建压过程中，固体推进剂药柱的受力状态复杂，会受到双轴拉伸、双轴压缩等多轴复杂应力作用。Potter 等［4］指出，采用单轴力学试验得出的强度判据式评判固体推进剂等各项异性材料在真实多轴受力状态下的失效情况，通常会带来较大偏差。因此，为精准评估SRM 药柱的结构完整性，必须开展双轴压缩等复杂应力加载下固体推进剂的力学性能试验。

目前，相较拉伸加载下的力学性能研究，国内外针对压缩条件下固体推进剂性能的试验和理论研究还比较少，且缺乏相应的统一标准［5］。采用常规准静态单轴材料试验机和圆柱型试验件，杨龙［6］开展了室温下准静态范围（1.7 × 10-4～1.7 × 10-1s-1）内固体推进剂的单轴压缩力学性能研究。为研究SRM 药柱在承受冲击载荷作用下的结构完整性，Zhang［7］以及Yang等［8］采用分离式霍普金森压杆（Split Hopkinson Pressure Bar，SHPB）装置开展了应变率高于100 s-1的固体推进剂单轴压缩力学性能试验。上述研究发现，固体推进剂的压缩强度和压缩模量等力学特性参数受应变率变化因素影响显著。强洪夫［9］以及赵文才等［10］的研究表明，固体推进剂的压缩性能和拉伸性能、单轴和双轴力学性能存在明显差异性，应力状态因素作用明显。为研究双轴应力状态下固体推进剂的强度准则，张亚［11］基于准静态双轴试验机和长方体试验件开展了不同加载速率下的双轴压缩试验，但未对推进剂试验件的构型进行分析计算和验证，也缺乏针对试验件变形过程中应力分布等问题的讨论。其次，由于测试原理的局限以及固体推进剂性能的复杂性，常规单轴试验机和SHPB 装置均无法直接有效地开展双轴动态加载下固体推进剂的力学性能试验。由于加载速率的限制，常规双轴力学性能试验机也无法开展动态加载下的力学性能试验。因此，目前仍缺乏针对动态双轴压缩加载下固体推进剂力学性能测试的试验方法，必须采用新的测试手段来开展相应的研究。

在开展材料的动态力学性能试验时，新型单轴高应变率液压伺服试验机具有明显优势。前期，王哲君等［12］基于该试验机开展了大量低温动态加载下固体推进剂的力学性能试验。为进一步满足基于该试验机开展动态双轴压缩加载下的力学性能试验需求，针对特定双轴压缩试验夹具和测试方法，本研究重点开展相对应的固体推进剂试验件的构型优化，给出满足双轴变形特性要求的最优构型，并采用高应变率液压伺服试验机开展动态加载下的双轴压缩试验，验证设计方法的有效性。

2 试验原理

基于力的分解原理，结合新型单轴高应变率液压伺服试验机及相适配的试验夹具，即可对合理构型的固体推进剂试验件施加动态双轴压缩载荷，具体加载方法如图1 所示。即随着试验机夹头竖直向下运动，可通过试验夹具对固体推进剂试验件施加力的作用，力的大小为F。由于夹具与固体推进剂试验件紧密贴合，且加载面彼此垂直，并受到运动学上的约束。因此，相应的固体推进剂试验件加载面上可受到比例为1∶1、载荷大小为F/ 2、位移为U/ 2 的双轴压缩作用，U是试验机沿竖直方向的位移。

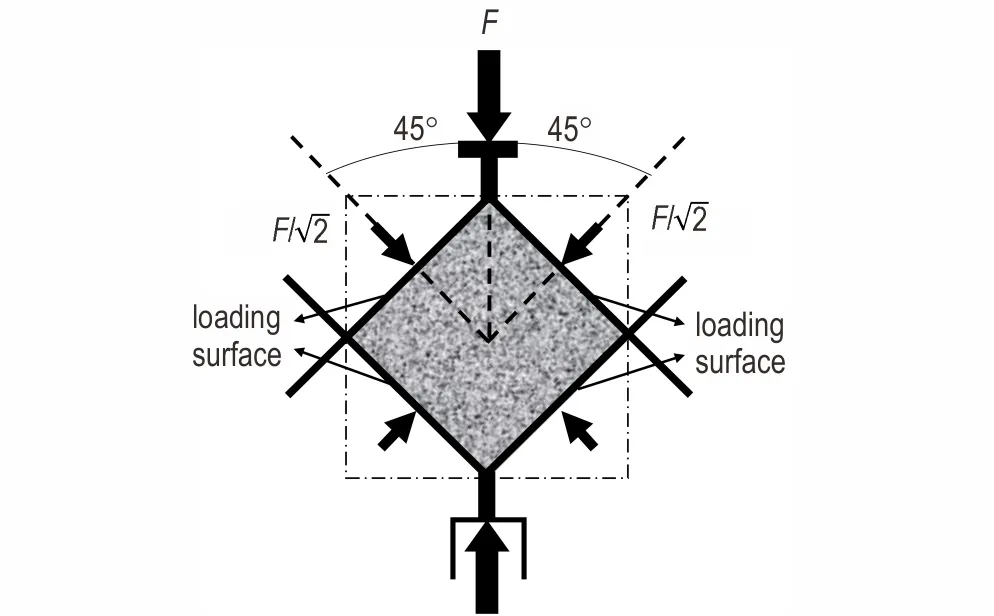
图1 试验件受力示意图Fig.1 Schematic diagram of force on the specimen

3 试验件设计

3.1 试验件构型及优化指标

基于上述试验原理，双轴压缩的试验件构型必须满足以下两个要求：（1）受力状态是双轴压缩，且试验件整体受力要尽可能均匀；（2）便于施加压缩载荷，构型简单，便于加工和制备。基于以上设计要求，借鉴JANNAF 标准［13］，拟采用长方体构型的固体推进剂试验件，但具体尺寸需进一步优化。参考王哲君等［14］前期开展单轴动态压缩加载时长径比为1 的固体推进剂试验件构型，将试验件设计为长高比（L/H）为1，长（L）和高（H）尺寸均为25 mm，并对宽度（W）进行优化，试验件示意图如图2 所示。

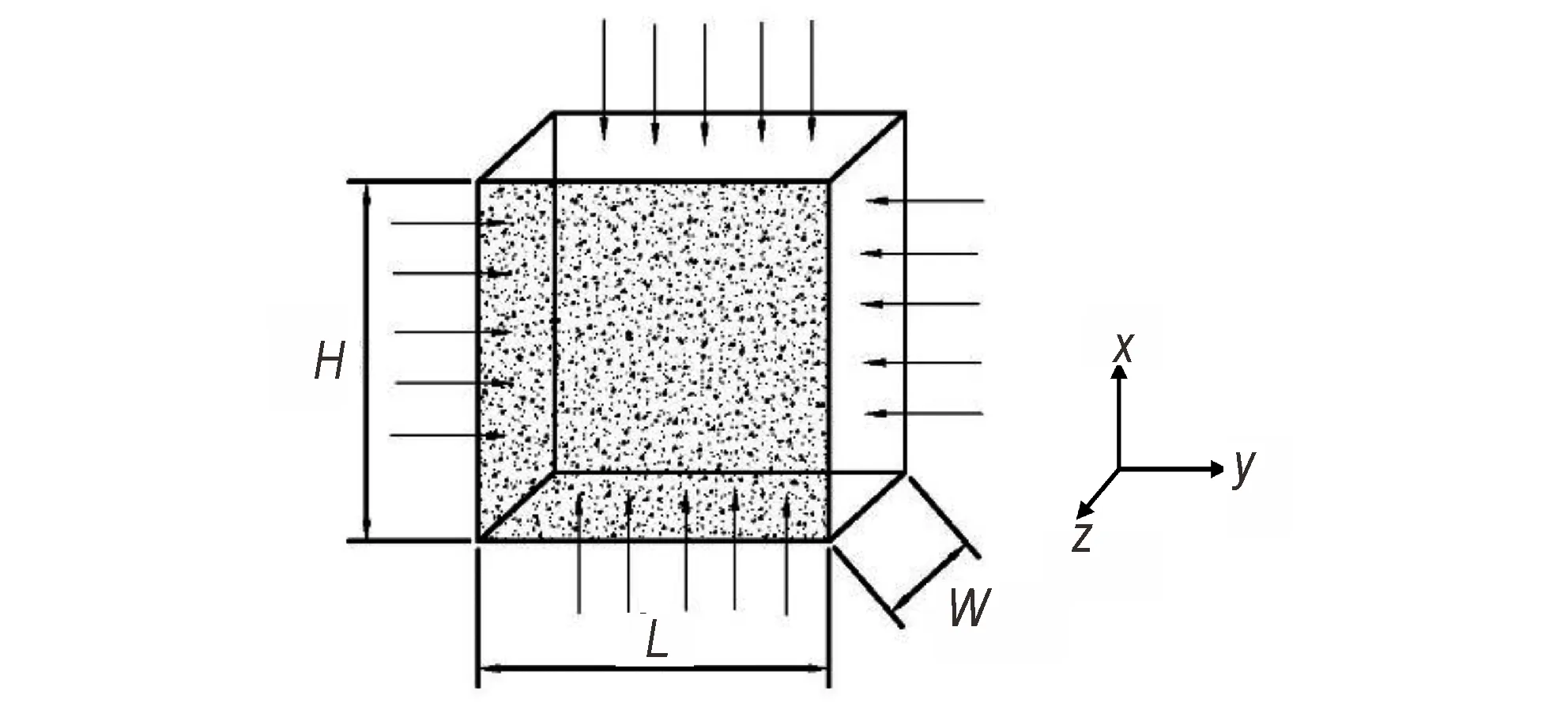
图2 试验件示意图Fig.2 Schematic diagram of the specimen

为定量评价不同构型方案的优劣，提出以下四个优化指标：

（1）平面应力平均值σˉ：用于衡量沿着非加载方向的试验件平面受双轴压缩加载时的应力水平。计算方法是求取典型截面（根据仿真结果的截面规律特征加以确定）对角线上均匀分布的N个点的应力平均值作为双轴加载平面应力平均值σˉ，即：

式中，σi为创建的路径上第i个点的Mises 应力，MPa。

（2）平面应力离散度CVs：用于表征该区域内试验件应力水平的均匀程度。离散度越高，均匀性越差，相应的试验结果可靠性越低。计算表达式为：

（3）整体应力稳定系数φ：用于表征试验件整体应力水平的均匀程度。数值越小，表明试验件的应力分布越均匀，测量结果准确性越高。数学表达式为：

式中，σˉz是沿z轴方向（即图2 宽度方向）上所有节点的Mises 等效应力平均值，MPa。

（4）应力集中系数α：试验件应力集中区域的应力最大值与均值的比值。该值越小，说明试验件应力集中现象越不显著，数学表达式为：

式中，σmax为试验件应力最大值，MPa。

3.2 有限元计算

为进一步确定试验件的最优构型，并分析不同试验件构型对双轴压缩试验结果的影响，采用ABAQUS软件开展有限元数值仿真计算。基于3.1 节初步设计的试验件构型尺寸，针对八种不同宽度下的有限元模型进行仿真计算，其宽度具体尺寸及物理模型如表1和图3 所示。

表1 仿真试验件宽度尺寸Table 1 Wide dimensions of simulated specimens

图3 试验件物理模型示意图Fig.3 Schematic diagram of the physical model for the specimen

数值仿真计算中，选取固体颗粒（AP/Al）填充质量分数88%的三组元端羟基聚丁二烯（HTPB）复合固体推进剂为研究对象，其本构关系采用基于Prony 级数的线粘弹性本构，级数n取6，各阶参数详见表2。网格划分采用C3D8RH 单元，共计25532 个单元。为实现双轴压缩，在试验件与下夹具接触两截面分别施加U1=0 和U2=0 的边界条件，与上夹具接触的两截面施加速度载荷，以50.5 mm·min-1（对应应变率为1/42 s-1）的速度加载，加载时间为4.2 s。材料属性的其他参数：泊松比ν= 0.4965。

表2 HTPB 复合固体推进剂本构关系的Prony 级数各阶参数Table 2 Prony parameters of constitutive relationship for HTPB composite solid propellant

3.3 结果分析

图4 为八种不同构型试验件在应变5%和10%阶段的Mises 应力云图。

由图4 可知，在不同的应变条件下，不同构型的推进剂试验件在双轴压缩时均会在边角处出现应力集中现象，且随着应变的增加，应力集中现象更加明显，但Mises 应力总体分布均匀，满足试验件设计的均匀性要求。在此基础上，进一步评判试验件受力状态是否为双轴压缩。

3.4 试验件受力状态分析

由图4 可知，沿z轴（即试验件宽度方向）的各个平面所处应力状态基本一致，因而在5%和10%应变下，选取中间平面为典型特征截面进行分析，其受力情况如表3 所示。

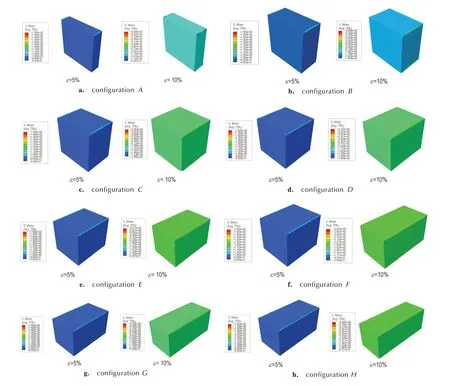
图4 典型压缩应变下的Mises 应力云图Fig.4 Mises stress contour at typical compressive strains

由表3 可知，当应变达到5%时，不同构型试验件沿载荷加载方向的平均正应力σˉxx和σˉyy近似相等，且最大相对误差δ不超过3.7%，表明受载方向上的应力比例近似为1∶1。此外，由表3 可知，Q值会随着宽度W的增加而不断减小，当减少至某一阈值时，非加载方向平均正应力σˉzz无法近似为0，即此时试验件处于三轴受力状态，不再符合双轴压缩试验件设计要求。当应变增加至10%时，仍然呈现出相似的规律性。鉴于σˉzz的值比较小，综合对照比例系数Q值的大小，只保留满足加载比例为1∶1 双轴压缩应力状态的A、B、C、D、E五种构型方案进行后续优化设计。

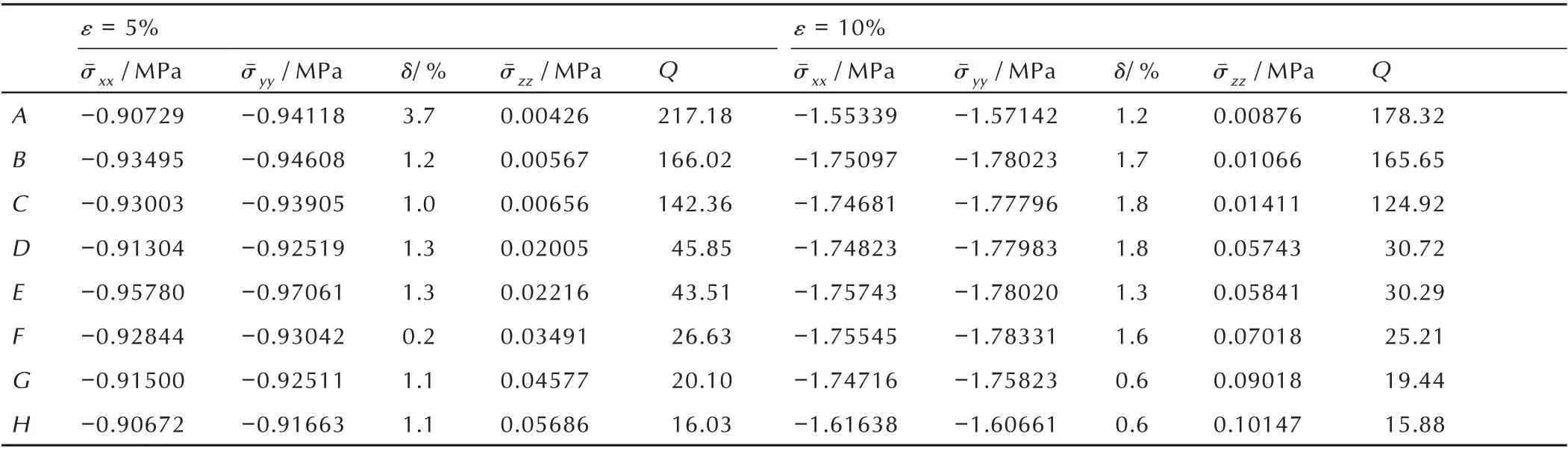
表3 试验件平面平均正应力值Table 3 The values of plane mean normal stress for the specimen

3.5 尺寸优化

为进一步比较A、B、C、D、E5 种构型方案的优劣，利用式（1）～（4）进行优化目标函数的计算，应变5%时试验件的优化目标结果如图5 所示。

由图5 可知，五种构型试验件的平面应力均值σˉ比较接近（图5a），试验件宽度变化造成的差异性不明显。其次，平面应力的离散度CVs随着宽度的增加而减小（图5a），当宽取25 mm 的时候，CVs最小，即正方体构型在典型特征界面上的应力分布均匀性最好。第三，随试验件宽度不断增加，整体应力稳定系数φ也呈现出逐渐递减的趋势（图5b），表明受压试验件整体的应力状态稳定程度随宽度（W）的增加而增强。最后，试验件应力集中系数随z轴方向上的长度增加而减少（图5b），表明应力集中对试验结果影响的程度也越小。

图5 优化目标参数值与宽度关系Fig.5 Relationships between optimization target parameter values with width

综上所述，宽（W）取25 mm 的长方体推进剂试验件构型，即边长为25mm 的正方体试验件构型为最优方案。

4 试验验证

4.1 试验材料及试验件

继续采用固体颗粒（AP/Al）填充质量分数88%的三组元HTPB 复合固体推进剂为试验对象。从表1 所示八种构型中选取三种典型尺寸进行试验验证，分别代表L/W＞1、L/W=1 以及L/W＜1 构型，相应尺寸下加工的推进剂双轴压缩试验件如图6 所示。

图6 三种典型构型尺寸试验件Fig.6 Specimens with three typical configurations

4.2 试验方法

在INSTRON160/100-20 新型单轴高应变率液压伺服试验机上开展试验，试验温度为常温。将图6 所示的HTPB 复合固体推进剂试验件放置于压缩夹具中间，以保证受力均匀对称。试验机加载速率定为35 mm·s-1（对应应变率为1 s-1），压缩总应变为10%，进行5 组重复试验，以保证数据可靠性。最终，试验机记录并输出相对应的载荷-位移曲线。对5 组试验数据进行均值并光滑处理，得到试验条件下的载荷-位移曲线如图7 所示。

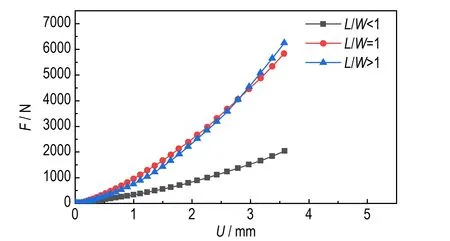
图7 三种典型构型HTPB 复合固体推进剂双轴压缩试验件的载荷-位移曲线Fig.7 Load-displacement curves of HTPB composite propellant specimens with three typical configurations in biaxial compression

4.3 试验结果与讨论

由图7 可知，三种典型构型的试验件均呈现出相似的变化规律，即载荷随位移增加而不断增大，并逐渐由线性过渡至非线性变化趋势。其次，试验件构型尺寸对载荷-位移曲线特性的影响规律性不明显。在此分析基础上，进一步采用式（5）和（6）求解相应状态下的应力及应变，确定是否存在尺寸效应。双轴压缩加载条件下的试验件应力-应变曲线如图8 所示。

图8 三种典型构型HTPB 复合固体推进剂双轴压缩试验件的应力-应变曲线Fig.8 Stress-strain curves of HTPB composite propellant specimens with three typical configurations in biaxial compression

式中，σ是名义应力，MPa；F是作用在夹具上的加载力，N；ε是名义应变；U是夹具沿着竖直方向的位移，mm；L0和W0分别为试验件原始的长和宽，mm。

由图8 可知，随着应变的增加，三种典型构型尺寸下的推进剂试验件均呈现应力随应变增加而不断增大的趋势。其次，当应变小于0.3%时，三种典型构型尺寸下的试验件承受的应力较为接近，但随着应变的进一步增加，试验件构型尺寸的改变对应力-应变曲线特性的影响变得更加显著。结合初始应变放大区域发现，L/W＞1 的试验件构型同L/W=1 和L/W＜1 两种构型的力学性能差异较大。主要是由于L/W＞1 的试验件构型Q值相对较小，此时试验件不再处于双轴受力状态，而是更加复杂的三轴受力状态。最后，在同一应变条件下，L/W=1 的试验件构型对应的应力值σ最大。此外，当应变增量Δε相同时，对应应力增量Δσ最大的仍是L/W=1 的试验件构型。因此选取L/W=1的试验件构型进行动态加载下的双轴压缩力学行为研究最具有代表性，进而验证了最优试验件构型设计的有效性。

5 结论

（1）提出了能够与单轴液压伺服试验机、试验夹具相配合，从而实现动态双轴压缩加载的固体推进剂试验件构型，并基于有限元数值仿真计算，获得了八种不同构型推进剂试验件变形的应力云图。结果表明，不同构型试验件在双轴压缩时的Mises 应力总体分布均匀，满足试验件设计的均匀性要求。

（2）在数值仿真计算结果的基础上，选取平面应力平均值、平面应力离散度、整体应力稳定系数和应力集中系数作为所设计固体推进剂试验件构型的优化指标。通过对比发现，长宽比为1，边长为25 mm 的正方体推进剂试验件为最优构型。

（3）成功开展了所设计的典型构型固体推进剂试验件的动态加载双轴压缩试验，结果发现，在0.3%应变以内，试验件尺寸效应表现不明显，但试验件尺寸效应会随着应变进一步增加而逐渐凸显，尤其体现在L/W＞1 尺寸构型的试验件上。此外，相同应变下对应的应力σ以及同一应变增量Δε下对应的应力增量Δσ均为L/W=1 尺寸构型下的试验件最大，进而从试验角度验证了数值仿真计算确定的L/W=1 最优试验件构型的有效性，可为后续进一步系统开展动态双轴压缩加载下固体推进剂的力学性能研究提供有力支撑。