基于改进TSVR的MIMO-OFDM系统信道估计及其原空间解法

李 朔，雷为民，张 伟

（1.东北大学 计算机科学与工程学院，辽宁 沈阳 110819；2.辽宁科技大学 电子与信息工程学院，辽宁 鞍山 114051）

新兴通信系统的发展对无线通信技术提出了较高的要求，对无线传输速率的需求增长迅速。由于无线信道在时域和频域上的衰落以及噪声的影响，在原有频率资源的基础上如何进一步提高频谱利用率，以达到提高无线通信速率的目的，仍然是一个开放性的问题。在诸多候选技术中，多输入多输出（Multi input multi output，MIMO）［1］技术可在不增加带宽的情况下消除天线间信号的相关性，增加数据的吞吐量。正交频分复用（Orthogonal frequency division multiplexing，OFDM）［2］技术是一种高速传输的多载波技术，由于信道被分成多个正交子信道，用于调制信息的子载波变窄，具有良好的抗多径衰落能力，可以降低信号间的干扰。正是由于这些优点，MIMO-OFDM［3］被目前新兴的通信系统所采用。在接收端，相干解调的方式比非相干解调具有更好的误码率性能，而信道参数的获取是接收端相干解调的必要条件。现有文献中给出了许多信道估计算法，如最小二乘（Least square，LS）估计法算法［4］，线性最小均方误差（Linear minimum mean square error，LMMSE）［5］及其改进算法，最大似然信道估计算法等。信道估计是影响MIMO和OFDM系统性能的关键因素。和传统的单天线情况下的OFDM系统相比，多天线的使用使得在接收端的子载波上接收到的信号都是多个畸变发射信号的叠加，使MIMOOFDM系统中信道估计更具挑战性。实际的移动无线信道具有非线性特征，但多数的解决方案采用的通信信道模型假定为线性的［6］，特别是在时域和频域都具有双选择性的信道情况下，如果仍然采用线性假设下的信道估计会降低估计性能［7］。因此，一些非线性方法被用于非线性信道估计［8］。

近年来，支持向量回归（Support vector regression，SVR）［9］被广泛应用于非线性关系的回归。该方法与深度学习等方法相比所需样本量小。根据Vapnik-Chervonenkis（VC）［10］的理论，非线性映射方法的采用可以将原本线性的SVR方法推广到非线性回归领域［11］。基本SVR及其大部分改进方法并没有考虑利用样本的先验信息，所有样本都被赋予了相同的权值，这样会降低系统的回归性能。基于以上考虑，本文提出一种改进加权孪生支持向量回归算法（Twin support vector regression，TSVR），并在此基础上设计MIMO-OFDM系统非线性信道频率响应估计算法，权值由K最近邻（Knearest neighbor，KNN）分类算法确定，并利用牛顿迭代算法在原空间对TSVR的目标函数进行求解，以提高系统泛化能力。

1 MIMO-OFDM系统模型

具有MT个发射天线和MR个接收天线的MIMO-OFDM系统，如图1所示。将输入数据X(k)进行空时编码，其第i个天线输出序列为Xi(k)（i=1，2，…，MT）。将该序列分成N个符号的块，并使用N点离散傅立叶逆变换（Inverse fast flourier transform，IDFT）转换。为了避免符号间干扰（Inter symbol interface，ISI），长度LC等于或大于信道阶数L的循环前缀（Cyclic prefix，CP）插入到每个块的头部。第i个发射天线的时域信号为xi(n)

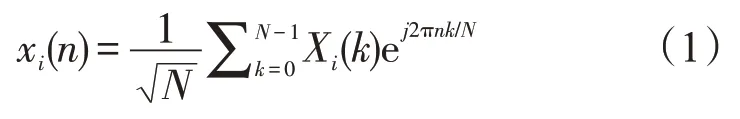
图1 MIMO-OFDM系统发射-接收框图Fig.1 Transmission and reception diagram of MIMO-OFDM system

式中：n=-LC,…,N-1；k=0,…,N-1。

xi(n)由发射天线发出，通过双选择无线信道，到达接收天线。在接收端，去除循环前缀后，MR个接收天线接收到的时域信号y(n)∈CMR，可以表示为

其中，v(n)=[v1(n),v2(n),…,vMR(n)]T是加性高斯白噪声（Additive white gaussian noise，AWGN），vi(n)的期望值和方差值分别为0和σ2，且v(n)各元素间是相互独立的。hi(n,l)=[h1(n,l),h2(n,l),…,hMR(n,l)]T是信道冲激响应向量。令Y(k)∈CMR为第k个子载波处除去CP后接收序列的频率响应向量

V(k)∈CMR是噪声v(n)在子载波k处的频率响应，I(k)∈CMR是由子载波k周围的子载波引起的载波间干扰（Inter carrier interference，ICI），在接收端，可以对双衰落信道进行均衡，并根据信道信息恢复发送的符号。

2 空时编码传输

为了获得分集增益，MIMO-OFDM系统发射端采用空时编码进行处理，并不失一般性地以两个发射天线和一个接收天线为例

式中：（·）*是复共轭算子；X1和X2分别表示天线1和2发送的两个信号；Xo和Xe分别表示要发送的信号X的奇、偶序列。

假设信道响应在连续的符号周期内保持不变。接收天线在频域中接收到的信号可以表示为

式中：Xe/o(k)、Ye/o(k)和Ve/o(k)表示偶/奇序列的第k个子载波处的发射信号、接收信号和噪声；H1/2(k)表示第1或2个发射天线与接收天线间在第k个子载波处的信道响应。

由式（8）得到导频子载波位置的信道频率响应估计值为

计算所有子载波上的频率响应，其估计值可以形式化地表示为

3 MIMO-OFDM系统信道估计

无线信道是非线性的，本文利用TSVR的非线性特性，采用KNN加权TSVR算法估计MIMOOFDM信道的频率响应。

3.1 导频子载波信道估计

用“导频符号”和“数据符号”分别表示插入导频的OFDM符号和没有导频的OFDM符号；“导频子载波”和“数据子载波”分别表示导频符号中的导频子载波和作为数据的子载波。为了实现空时编码中的信道估计，导频符号在时域成对出现。导频符号在时域中的位置集合表示为{nΔt,nΔt+1|n=0,…,Nt/2-1}，其中偶数Δt≥2是导频符号间隔，Nt是导频符号数。导频子载波的位置集合描述为{mΔf|m=0,…,Nf-1}，Nf和Δf分别是一个OFDM符号中的导频数和导频频率间隔。图2给出了导频插入方案。

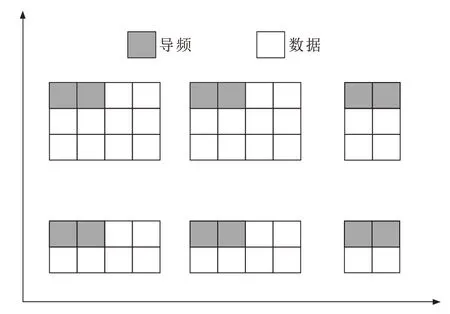
图2 导频插入方案Fig.2 Scheme of pilot insertion

3.2 加权TSVR信道估计

给定一个训练集S={(τ1,r1),(τ2,r2),…,(τm,rm)}，其中导频所在时域和频域的位置作为训练输入：τk∈R2，导频采样点的冲激响应作为输出：rk∈R，k=1,2,…,m，构成一个训练输入输出对(τk,rk)，m是样品编号。输出向量可以表示为R=(r1,r2,…,rm)T∈Rm，训练输入为T=(τ1,τ2,…,τm)T∈Rm×2。MIMOOFDM系统的信道响应的回归函数为

式中：f1(τ)和f2(τ)分别为孪生支持向量机的下界和上界回归函数；K是核函数；g1,g2∈Rm和δ1,δ2∈R是待估计参数。

信道估计优化问题的目标函数可以表示为

式中：c1、c2、c3、c4、ϵ1和ϵ2是用户指定的正参数；e是适当维数的“1”的列向量；D=diag(q1,q2,…,ql)是一个小波权重对角矩阵；q∈Rm和D=diag(q)∈Rm×m为权值。

用KNN算法计算权值向量q=[q1,q2,…,qm]T

式中：A和σ分别是高斯函数的振幅和标准差（=[R̂1,R̂2,…,R̂m]T），表示输出R（=[r1,r2,…,rm]T）经KNN预处理后得到的矢量，R̂可由KNN算法计算得到［12］。

3.3 牛顿迭代法

有约束优化问题（12）和（13）可转化为无约束优化问题

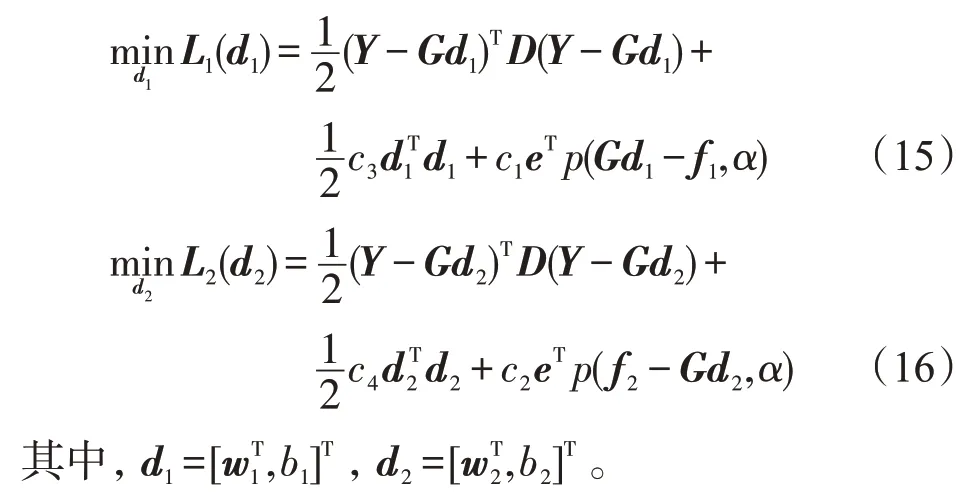
已知矩阵G=[k(A,AT)e]是非线性的例子。令f1=Y+ε1e，f2=Y+ε2e。其中，光滑函数

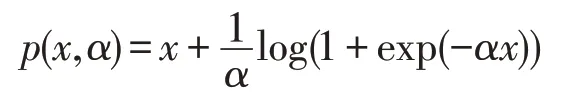
式（15）和式（16）的解可通过求梯度向量∇L1(d1)=0和∇L2(d2)=0得到，即

结合式（17）和式（24），应用牛顿法求解式（15）和式（16）。求解的迭代过程

4 仿真实验结果

为了证明所提出的改进的加权TSVR用于MIMO-OFDM系统信道估计的性能，将其与几种常用的信道估计算法进行比较，采用线性插值算法、经典的TSVR算法和本文所提出的算法一起进行仿真研究。

仿真参数：调制方式为16-QAM，载波频率fc=2.15 GHz，一个码元内子载波数N=128，CP长度为5，采样间隔Ts=72µs，移动速度v=120/350 km/h。加权改进TSVR算法中的常数设置为c1=c3=0.1，c2=c4=0.1。

在仿真中，导频同时在时域和频域中插入。选择高斯函数作为改进加权TSVR算法和经典TSVR估计的非线性映射核

式中：η是高斯函数的宽度或方差。

选择误码率（Bit error rate，BER）准则来评估算法的性能

式中：ne是二进制的错误数据个数；nT是二进制总数据个数。

图3给出了改进的加权TSVR对非线性信道回归的拟合情况。本试验中，信噪比（Signal noise ratio）SNR=20 dB，多径数L=8，移动速度v=120 km/h，星点作为训练样本的有噪声信道响应。实验结果表明，本文提出的算法能较好地拟合信道响应。

图3 改进的加权TSVR对信道响应的回归Fig.3 Regression of improved weighted TSVR to channel frequency response

本文算法与线性插值法、经典TSVR算法以及已知信道参数的BER曲线如图4所示。在4种计算条件下，随着信噪比的增加，三种算法的误码率都明显降低，并且本文的算法误码率最低。说明SVR具有非线性关系的回归优势。运动速度越快，或者插值间隔增大，三种算法的误码率都有所提高，但本文算法依然最接近已知信道参数。因为相对运动速度越快，ICI越大，导致误码率高。时间间隔和频率间隔的增加降低了训练数据的信息量，导致回归性能下降。

图4 上述4种情况下的误码率Fig.4 Bit error rates in four cases above

5 结论

本文提出了基于改进的加权TSVR算法的MIMO-OFDM信道频率响应估计器。利用在时域和频域均匀插入的导频信号对信道响应进行估计。在发射端，在数据中插入导频信号，并经过OFDM调制后由天线发送。在接收端，接收的数据进行解调与解码，利用基于改进的加权TSVR的估计器对数据进行插值。该算法利用KNN算法计算样本权值，并将其加入改进的目标函数中。优化问题经牛顿迭代方法计算获得。仿真实验表明，本文提出的算法误码率低于经典TSVR算法，具有良好的估计性能和抗噪声能力。证明该方法在非线性无线通信信道估计中的有效性。