基于二阶分段式的Apriori算法优化

刘丽娜，吴新玲,2

(1.广州工商学院 计算机科学与工程系，广东 广州 510850；2.广东技术师范大学 计算机科学学院，广东 广州 510665)

0 引 言

数据挖掘模型主要有分类模型、聚类模型、回归模型和频繁项集[1]。频繁项集的关联规则算法——Apriori算法由Rakesh Agrawal和Ramakrishnan Srikant提出[2]，但后期随着研究的不断深入以及数据量及其复杂度的不断增加，仅限于两种属性值的数据集挖掘、过多的产生候选频繁项集和频繁遍历数据集导致内存溢出等弊端也日益突出。

Apriori算法的改进主要集中于减少I/O消耗和压缩数据量。文献[3]通过构建数据集矩阵压缩数据量提高算法执行效率，但对数据集原型的约束较高，且对多维度多属性值数据的挖掘模型并未说明。文献[4]Eclat算法利用数据量远大于数据集维度的特点提出了行与列的转置存储，压缩数据集，但该方法不适用于分析数据集较小或事务项小于数据集维度的数据。文献[5,6]利用Hadoop并行计算框架分散数据量，验证了并行计算的优势，但仅靠并行计算并不能让执行效率最大化。文献[7]提出了依托Spark计算框架的Apriori改进算法YAFIM，该算法利用哈希树判断候选频繁项集减少I/O消耗，但因其频繁调用算子且产生大量候选频繁项集使得算法效率提高有限。文献[8] 在文献[7]的基础上提出IABS算法，该算法结合文献[4]行与列的转置结构，然后再使用YAFIM算法生成规则，虽然IABS算法的执行效率较YAFIM算法有所提高，可扩展性也更强，但YAFIM算法原有的缺陷并未消除。文献[9,10]通过构建布尔数据集矩阵压缩数据量，同时加权减少内存和I/O，但未分析对加权后有效规则完整性的影响。文献[11]提出I-Apriori算法，该算法在YAFIM第二阶段中采用布隆过滤器代替哈希存储结构减少候选频繁项集生成，但在该过程中对改用布隆过滤器存储数据的耗时并未加以考虑。

本文依托Spark计算框架提出一种支持多维多属性值数据集的二阶分段式Apriori算法优化模型。一阶聚类离散，降低数据拟合度提高数据差异性，二阶分析形成规则。该模型先后对K-Means聚类算法和Apriori算法进行优化改进，二阶以一阶的聚类结果作为输入，最后通过分析和实验验证算法的执行性能。

1 二阶分段式算法实施方案

二阶分段式算法采用先聚类后分析的模式，一阶对聚类算法K-Means进行并行设计，然后聚类数据集；二阶对Apriori算法进行优化，然后将一阶的聚类结果作为优化后的Apriori算法输入，最后分析数据集得到关联规则。

设数据集D={I1,I2,…,In|n≥1}， 其中事务项Ii={vi1,vi2,…,vim|1≤i≤n，m≥1}， n为事务项总数，m为数据集的维度数。假设第j个维度对应的值域为Aj，则vij∈Aj。

1.1 构建K-Means算法优化模型

1.1.1 K-Means算法介绍

K-Means是一种基于划分无监督型算法，该算法可以将相似的数据进行聚类重组[12]，其原理分为3个阶段。第一阶段先确定数据集质心Ic及其聚类数量k，然后通过计算各个数据点Ii到质心Ic的欧几里得距离[13]d (Ii,Ic) (其中Ii≠Ic且Ii、Ic∈Dc，Dc为以Ic为质心的数据集，Dc⊂D)， 数据点Ii根据就近原则分配到相应的质心堆中直至所有数据点分配完毕；第二阶段则是重新计算各个堆中的均值以调整质心，然后重新分配数据点；第三阶段不断重复计算调整质心Ic，最后通过误差平方和函数[14]φSSE衡量聚类的拟合度。

欧几里得距离d(Ii,Ic) 的计算公式如式(1)所示

(1)

聚类收敛性衡量指标误差平方和函数φSSE的计算公式如式(2)所示

(2)

式(1)和式(2)中， 1≤i≤n，Dc为以Ic为质心的数据集，Ii为事务项，即聚类点。

1.1.2 K-Means算法优化原理

传统的K-Means算法一般多为分析只有两种属性值的数据集，且均在单机进行，受数据多样性约束，算法在计算调整质心时容易造成内存溢出等问题。本文依托基于内存的Spark计算框架提出结合Spark和K-Means的优化算法——SK-Means(K-means algorithm based on Spark)对原K-Means算法进行并行化设计。基于内存的Spark计算框架可以分布计算质心点，然后通过manager节点调整质心减少内存溢出风险，K-Means算法的迭代计算利用Spark计算框架各节点的并行计算能提升执行效率，且在设计上增加考虑了数据的多维度多属性值因素。

该优化算法以“总-分-总-分”的模型对SK-Means算法进行设计，如图1所示。首先，确定k的取值与质心点，计算聚类的误差平方和φSSE′，根据手肘法[15]选取最优聚类数k，随着聚类数k的增大误差平方和φSSE′会逐渐下降形成类似于手肘的弧度，当曲率最高时k的取值最佳；然后选取初始质心Ic={I1,I2,…,Ik|1≤c≤k}， 并将其存储为全局变量，由于每个数据点与质心点的欧几里得距离是单独计算的，因此，可以采用IClass算子计算各数据点到质心点的欧几里得距离d(Ii,Ic)′， 以就近原则将该数据点分配到所属聚类集Dc中，Dc={D1,D2,…,Dk|1≤c≤k}， 直至所有数据点聚类结束；最后，以KCount算子重新计算每个聚类堆Dc的质心I′c， 替换原全局质心变量，重复以上过程对数据点进行重新计算聚类直至聚类质心I′c≈Ic或达到迭代阈值，输出聚类结果。

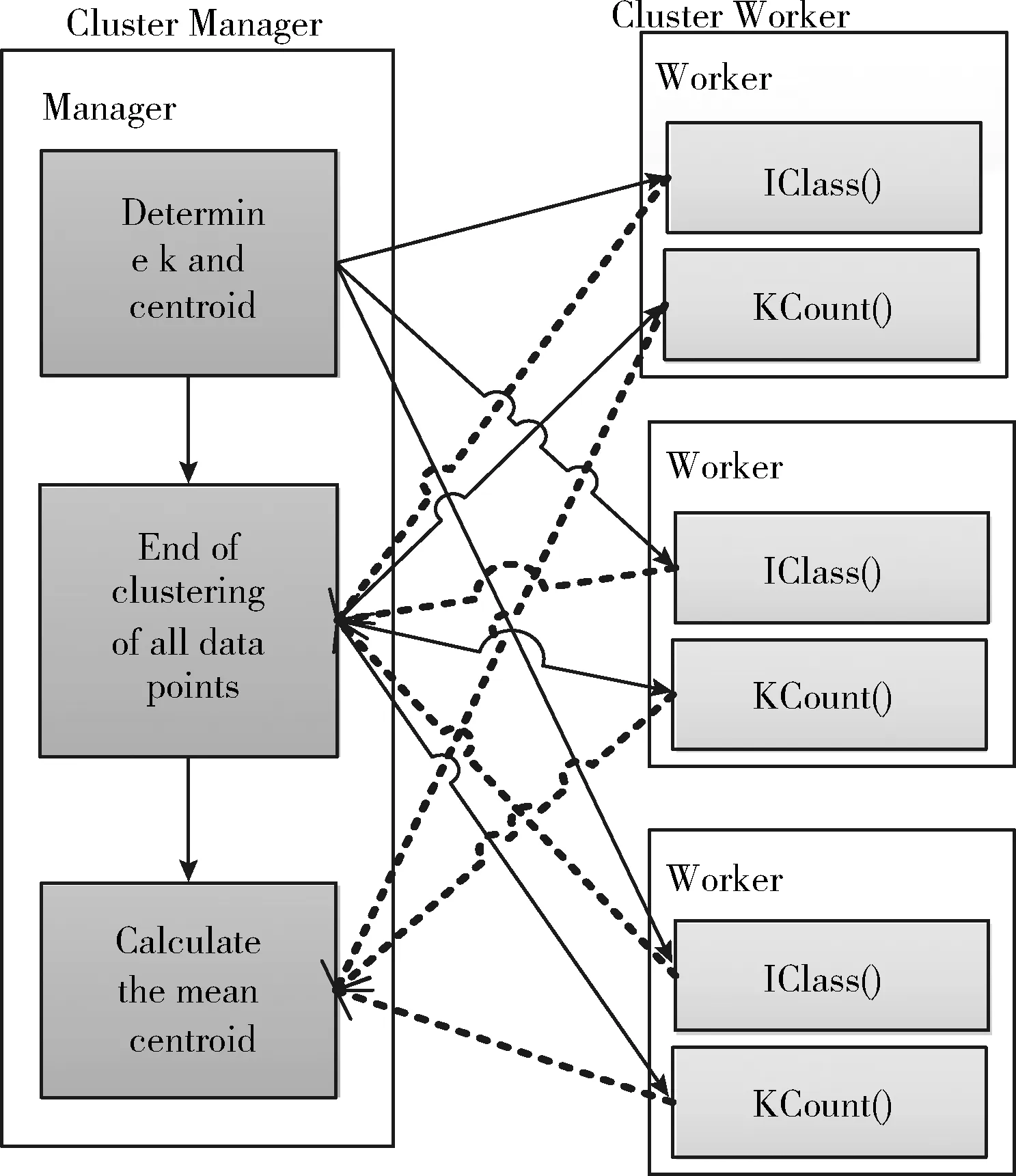
图1 SK-Means并行设计原理

数据点Ii(vi1,vi2,…,vim) 和质心点Ic(vc1,vc2,…,vcm) 的欧几里得距离d(Ii,Ic)′ 的一般性计算如式(3)所示，而多维多属性值误差平方和φSSE′的一般性计算则如式(4)所示。

多维度多属性值的欧几里得距离推导公式

(3)

多维多属性值误差平方和的推导公式

(4)

在式(3)和式(4)中，其中，m为数据集维度， 1≤j≤m，c为质心点所在行数，i为任意点所在行数，vij为事务项中的属性值。Dc为以Ic为质心的数据集，Ic为质心点。

1.1.3 SK-Means算法实现

RStudio为R语言提供免费开源的跨平台集成开发环境，具有大量图形类型绘制和统计方法支持语法编程的多种特色功能。SK-Means算法利用R语言在RStudio平台调用IClass算子计算距离进行聚类和KCount算子计算聚类质心，均值质心不断迭代生成RDD。算法首先确定最佳聚类数k，如未确定k则直接进入算法输出1至n(n为事务项总数)个聚类点下的φSSE′值，即遍历计算最佳聚类数k，输出最佳聚类数，算法往下计算聚类结果；若已确定最佳k值并输入，则输出聚类结果，算法主要伪代码如下：

算法1： SK-Means算法

输入： 数据集D和k或直接回车 //如已确定最佳聚类数k则输入k值， 未确定k则直接按回车

输出： 已聚类的数据集Di

(1)ifk==null //如果k值为空

(2) fork=1 to n

(3) 从D中选取k个质心：I1,I2,…,Ik;

(4) forc=1 tok

(5)Dc=Ø; //初始化聚类集

(6) IClass(Ic); //执行IClass算子， 计算各点的欧几里得距离d(Ii,Ic)′， 对各点进行聚类

(7) end for

(8) forx=1 to m //维度遍历

(9) fory=1 to n //属性值遍历

(10)I′c=∑vcxy/n; //重新计算质心

(11) end for

(12) KCount(I′c); //执行KCount算子， 如果质心I′c与原质心Ic不等或未达到阈值则更新， 相等则跳过

(13) Count φSSE′; //计算多维多属性值误差平方和

(14) Output φSSE′andk;//输出误差平方和及最优聚类数

(15) end for

(16) end for

(17) else

(18) forc=1 tok

(19)Dc=Ø;

(20) IClass(); //执行IClass算子， 计算各点的欧几里得距离d(Ii,Ic)′， 对各点进行聚类

(21) OutputDc; //输出聚类结果

(22) end for

1.2 构建Apriori算法优化模型

1.2.1 Apriori算法介绍

当频繁项集中的规则同时满足最小支持度Sup_Min和最小置信度Conf_Min则该规则为强规则，规则R(vix→viy) 的支持度Sup和置信度Conf的计算公式如式(5)和式(6)所示

(5)

(6)

其中，i为事务项中的某一项，1≤i≤n，n为数据集D中的事务项总数， R(vix→viy) 为属性值vix推出viy的规则，x、y属于自然数x≠y且x、y≤m， m为数据集的维度总数。

1.2.2 Apriori算法优化原理

Apriori算法执行效率低且在以往的优化中大部分集中考虑维度只有两种属性值的数据集分析，而对多维度多属性值的数据集研究较少，或未明确说明。针对以上问题提出了KIApriori(improved Apriori algorithm combined with K-Means)，该优化算法以改进后的SK-Means算法聚类结果作为输入，同时设计字典表存储多维多属性值数据集以达到压缩数据量的目的，之后对各事务项进行滚动“与”操作并统计支持度等数据，减少了数据集的扫描次数。

KIApriori算法与SK-Means算法同处于Spark计算框架进行，数据存储依赖于HBase，一般多维多属性值数据存储模式见表1。

表1 多维多属性数据集存储模式

KIApriori算法中二阶Apriori算法的优化原理分为两个环节。第一个环节是构建字典表，首先统计各元素在数据集中的计数，之后将数据集字典表化，字典表的构建根据数据集的维度按1∶1建字典表中的列，即一个维度在字典表建一列，字典表包含一个维度的所有属性值，并且所有属性值在字典表中唯一。其中，字典表中的ID为整型数据，ID在所在维度字典表中唯一，但在各维度中不唯一。第二个环节是“与”计算，该环节类似于地球的“公转”与“自转”执行数据集的“与”操作，“公转”即执行操作时由1至字典表最大ID值IDMAX将事务项中与ID值相同的属性值替换为“1”，其它值替换为“0”进行向下滚动式 “与”操作。“自转”则是在ID值第一轮“1”替换后，事务项向下进行“与”滚动。在每一次“与”操作时设置计数器自增，最后根据计数与项集数得出频繁项集，即关联规则。

1.2.3 KIApriori算法建模设计及实现

KIApriori算法的支持度KSup设计如式(7)所示

(7)

其中，Count为事务项 “与”操作的计数，n为事务项总数。

KIApriori算法的置信度KConf设计如式(8)所示

(8)

式(8)中，Count(R(vix→viy)) 为规则R(vix→viy) 的“与”操作计数，Count(vix) 是数据集字典表化前属性值vix的计数。

定义1 项集数：项集数φ为频繁项集中关联的属性值个数。频繁φ项集Lφ中的项集数φ计算如式(9)所示

(9)

其中， 0≤i≤(m-1)， m为数据集维度总数，AND[i] 为存放事务项“与”操作的结果的数组。

该算法依托Spark计算框架，以SK-Means优化算法的聚类结果作为输入，主要算法设计如下：

算法2： KIApriori算法

输入： 已聚类的数据集D， 最小支持度Sup_Min， 最小置信度Conf_Min

输出： 频繁项集、 支持度和置信度

(1)fori=1 to n //遍历所有事务项

(2) forj=1 to m //遍历所有维度

(3)Count(i);//计算每个属性值的统计数

(4) if(Count(i)<=Sup_Min)

(5) deletevij;//对于统计数小于最小支持度的属性值进行第一轮剪枝

(6) if(vij!=v(i-1)j) //构建字典表T

(7) ID++;

(8) T(ID)=vij; //存储字典表值

(9) if(vij=j)

(10)vij=1; //涉及 “与” 操作事务项转换为布尔值

(11) else

(12)vij=0;

(13)φ=Sum(Ij&Ij-1)；//构建函数， 计算与结果中所有值为“1”的和

(14)Cφj=Oper(Ij&Ij-1); // Oper函数执行事务项之间“与”操作， 如φ结果为0则Count(i)计数进行自减，否则存储二维候选频繁项集Cφj，j等于字典表中的ID标记sign， 以便还原属性值原内容

(15) fork=0 to IDMAX-1 // IDMAX为字典表最大的ID值

(16) if(((i/n)>=Sup_Min)&&((i/Count(j))>=Conf_Min)) //检查符合最小支持度和置信度并进行支持度与置信度计算

(17)Supφ=i/n;Confφ=i/Count(j); //分别用Supφ，Confφ存储频繁项集的支持度与置信度

(18)Lφ=Match(Cφj,k);// 还原频繁项集

(19) 输出Lφ频繁项集;

(20) 输出SupφandConfφ; //输出支持度及置信度

(21) end for

(22) end for

(23)end for

2 应用实现

2.1 数据预处理

本文结合工作实际，以广东若干高等院校2014届至2018届共5届的毕业生为研究对象，收集教务管理系统、学生就业信息、校外考证数据、学生选课系统、图书管理数据和校园一卡通管理系统中的相关数据构建数据集。为了提高挖掘规则的鲁棒性，需对数据进行清洗和概化[16]，实验采用“数据选择-数据清洗-数据转换-数据集成”的流程对数据进行预处理。

本实验收集的数据记录共151 107条，除去中途休学退学的63个学生，该部分数据占总数的0.04%，亦属于离群噪点，去除之后对数据整体的有效性及完整性的影响几乎可忽略。此外，对部分数据进行降维，例如成绩的区间为[0,100]，概化为不及格[0,60)，及格[60,70)，中等[70,80)，良好[80,90)和优秀[90,100]这5个级别以消除多余属性对挖掘结果的影响。

本实验数据经过清洗后得到约15万个往届毕业生的数据记录，涉及37个维度，通过数据概化后得到148种属性，总大小约16 MB，选取部分已预处理的数据集见表2。

表2 多维多属性数据集实例

2.2 一阶聚类离散

实验数据集属性值多且构成复杂，直接对其进行分析可能存在挖掘效果拟合高稳定性低等问题。因此对数据集进行聚类离散有利于增强数据特征差异性和发现鲁棒性强规则，同时提高规则形成效率。

2.3 二阶分析

在第二阶段中，设最小支持度Sup_Min=0.4, 首先计算每一数据集中各维度属性值的计数，然后根据式(7)将各计数结果除以事务项总数7对比支持度剪去低于支持度的事务项从而压缩数据集。

在表2中剪去不符合支持度的事务项，然后将符合条件的数据集字典表化，字典表中的ID唯一，每一个维度的每一个属性值都对应一个ID。该实例中字典表的构建见表3。

表3 字典

剪枝后的数据集根据字典表3进行转换实现数据集的再次压缩，将属性值对应字典表转换结果见表4，即将符合支持度计数的各个维度的属性值替换成字典表中对应的ID号。

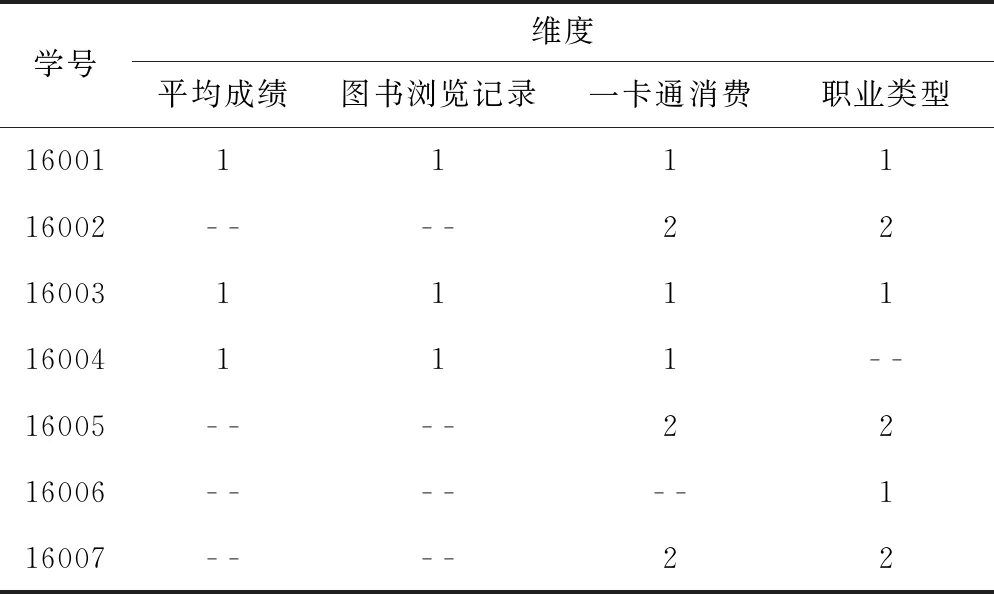
表4 数据集字典表转换

该步骤中第一次从“1”开始替换第一行，即第一行中的所有“1”替换为“1”，其它值替换为“0”，记录标志sign=1，sign标记所替换的值以便于规则表达式还原。该实例中，事务项的第一行“16001”(1,1,1,1)被替换之后为“16001”(1,1,1,1)，然后将第二行“16002”(- -,- -,2,2)取出并替换，替换后为“16002”(0,0,0,0)，然后执行事务项“16001”和“16002”的“与”操作，结果为“16001”&“16002”(0,0,0,0)，然后取出“16003”(1,1,1,1)，替换之后为“16003”(1,1,1,1)，再和替换后的第一行“16001”(1,1,1,1)“与”结果为“16001”&“16003”(1,1,1,1)，然后再和“16004”执行“与”操作，结果为“16001”&“16004”，以此类推，“16001”再与“16005”、“16006”和“16007”进行“与”操作，然后将“与”结果再一一向下进行“与”操作直至最后一项，如“16001”&“16003”(1,1,1,1) 和“16004”执行“与”操作结果为“16001”&“16003”&“16004”(1,1,1,0)。同理，“16002”与之后的记录进行同样滚动“与”操作。然后执行“公转”，即将“2”替换为“1”其它值替换为“0”进行向下滚动执行，记录标志sign=2，以此类推直至最大ID值IDMAX。

在进行一次“与”操作时，如“与”结果为0(即φ为0)则计数器Count减1否则加1，若 (Count/n)≥Sup_Min， 则依次可得到各项频繁项集。频繁φ项集Lφ中的项集数φ等于“与”结果中所有值的和。例如，计数器Count=3，记录标志sign=1，而事务总数n=7，则 (3/7)>0.4 (最小支持度)，“16001”&“16003”&“16004”(1,1,1,0)，则项集数φ=1+1+1+0=3， 即频繁3项集L3={1,1,1,0}[sign=1]， 一一对应各维度为L3={“平均成绩”*1,“图书浏览记录”*1,“一卡通消费”*1,“职业类型”*0}={“平均成绩”,“图书浏览记录”,“一卡通消费”}， 标记sign=1对应字典表中ID=1的元素，因此，频繁3项集L3={“平均成绩”.“优”,“图书浏览记录”.“频繁”, “一卡通消费”.“消费级别3”}， 由此得到频繁项集。

3 算法及实验结果分析

3.1 算法复杂度分析

K-Means算法的时间复杂度如式(10)所示

TCK-Means=O(k*n*Iteratetime*Td(Ii,Ic))

(10)

其中，k为聚类数，n为事务项总数，Iteratetime为算法迭代次数， Td(Ii,Ic) 为计算点Ii到点Ic的距离所花费的时间。而并行设计后的SK-Means算法在多个节点运行，若Spark中的节点数为Num，每个节点完成的IClass算子次数为Times，则SK-Means算法的时间复杂度如式(11)所示

(11)

从时间复杂度上分析，SK-Means算法比原K-Means算法在执行时间上具有明显优势。

Apriori算法复杂度如式(12)所示

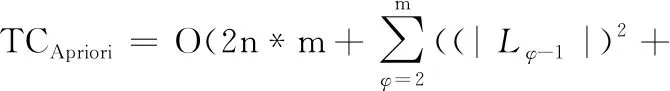
(12)

其中，n*m为第一次扫描数据库各事务项计数花费的时间，第一次剪枝花费时间亦为n*m，故有2n*m， |Lφ-1| 为生成候选频繁φ项集Cφ的连枝时间， n*|Cφ| 为计算Cφ各项计数的时间， |Cφ|2为Cφ的剪枝时间。

KIApriori算法复杂度如式(13)所示

(13)

其中，第一次计算扫描数据集和剪枝所花费的时间与原算法同为2n*m，而构建字典表和数据集转换的时间复杂度为n*m*IDMAX，算法滚动“与”操作生成频繁项集的时间复杂度为n*m*IDMAX，最后对比字典表还原频繁项集的时间复杂度为m*IDMAX*|Lφ|。

为验证改进后的KIApriori算法优势，以式(12)减式(13)进行验证。假设最差情况所有的候选项集没有剪枝，即 |Cφ|≈|Lφ|≈|Lφ-1|≈n则TCApriori-TCKIApriori=(L12+…+Lm-12)+n(C2+…+Cm)+(C22+…+Cm2)-2n*m*IDMAX-m*IDMAX(L1+…+Lm-1)-TCSK-Means=3n3-2n*IDMAX*m-m*IDMAX* n2-TCSK-Means=n2(3n-2m-m*IDMAX-k)。

n、m、IDMAX及k的大小决定KIApriori算法的适用情况，特别是数据量， (n/IDMAX)/n>Sup_Min， 否则属性值会在第一次扫描计算剪枝时被剪掉，故IDMAX<(1/Sup_Min)≪n， 聚类数k亦然，一般情况下数据集维度数m≪n， TCApriori-TCKIApriori>0， 而当数据量较小，即n≤(2 m+m*IDMAX+k)/3时，KIApriori算法的优势不明显，但当数据量越大时算法优势正比增长。

3.2 实验结果分析

本实验依托青岛青软实训教育科技股份有限公司合作平台提供的虚拟机，采用一个主节点5个从节点构建集群。Master节点和slave节点均用64位的CentOS7操作系统，主频2.66 GHz四核，内存4 GB软件环境组合Hadoop2.6+Spark2.1+JDK1.8+SparkR。为验证算法的执行性能，本实验将数据集拷贝至5*107条，数据维度及属性不变，得到总大小约5 GB的数据集。分两个阶段对优化后的SK-Means 和KIApriori算法进行分析。

(1)SK-Means算法实验结果分析

以传统的K-Means算法对比优化后的SK-Means算法，取UCI数据库中的wine、heart、Iris、letter和pima数据集的准确率和执行时间对比衡量算法性能，如图2、图3所示。

图2 SK-Means与K-Means算法准确率对比

图3 SK-Means与K-Means算法执行时间对比

由图2对比可以看出，SK-Means算法不但没有消减原K-Means算法的聚类效果且聚类准确率更高，SK-Means算法的准确率平均值比原K-Means算法高约32%。在图3中，SK-Means算法与原算法在不同数据量，不同质心k值的运行时间上，由于SK-Means算法受多维多属性数据集的多样性约束，在数据量较少时其优势不明显，但在分布式并行计算框架下随着数据量和聚类数的增加其聚类速度明显提高。

(2)KIApriori算法实验结果分析

该阶段的实验首先以Spark计算框架执行原Apriori算法，然后执行无K-Means算法加持但字典表化的Apriori优化算法，即不以SK-Means的聚类结果作为输入，直接执行二阶的优化后的Apriori算法(简称IApriori算法)，最后执行KIApriori算法。当最小支持度和置信度Sup_Min=Conf_Min=0.05时，在相同测试条件下弹性执行Apriori、IApriori和KIApriori这3种算法以对比评估其性能，各算法的执行时间不同节点数执行时间对比如图4、图5所示。

图4 不同算法执行时间对比

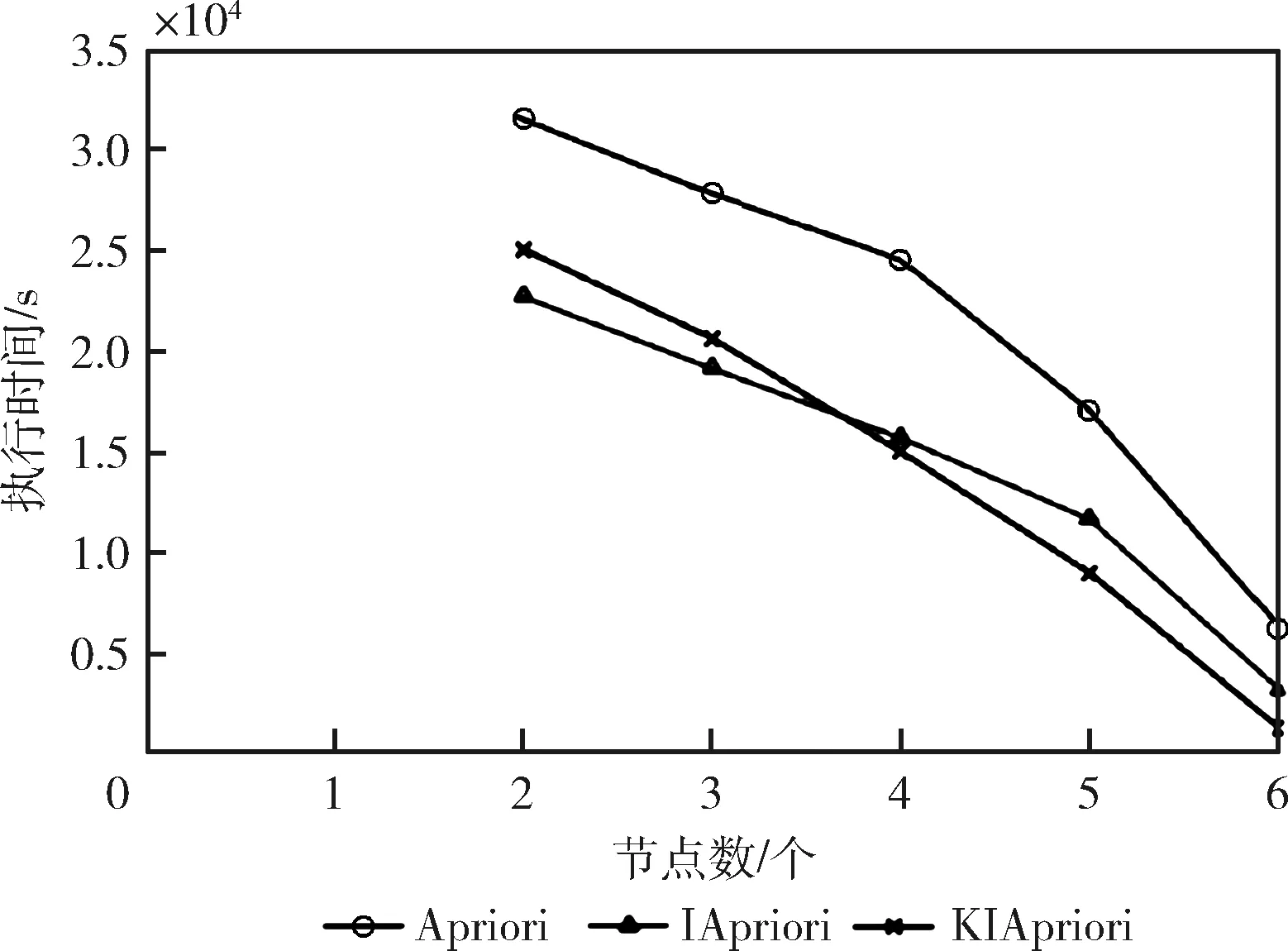
图5 不同算法不同节点数执行时间对比

从图4可以看出未优化的Apriori算法随着数据量递增其运行效率明显低于优化后的IApriori算法，执行时间几乎是IApriori算法的两倍。同比无K-Means加持的IApriori算法和有K-Means加持的KIApriori算法，因KIApriori算法在一阶时耗费一部分的时间执行SK-Means聚类，因此在处理数据量较少的情况下其运行效率不高，此时适用IApriori算法。但随着数据量的不断增加，其执行效率优势逐渐突出，在该实验后期，当数据量达到3 G的“拐点”时，KIApriori算法相对于IApriori算法执行效率提高47%以上。

而在不同节点数相同数据量的对比图5中，Apriori算法执行时间明显高于其它两种算法。对比IApriori和KIApriori 算法，因为节点数较少，使得前期聚类优势不明显，当节点数越接近聚类数时KIApriori算法的执行效率越高。

4 结束语

本文在基于内存计算的Spark并行计算框架下，提出了二阶分段式KIApriori算法模型，一阶聚类离散去除离群点压缩数据集增强数据差异性提高算法的规则生成效率，二阶构建字典表再次压缩数据集，“与”操作简化连枝剪枝去候选频繁项集降低I/O和内存消耗。该改进算法适用于分析各种结构化大数据集，数据量越大算法优势越明显。通过算法分析及弹性实验分析结果表明，KIApriori算法在大数据分析中有较高的分析效率和良好的可伸缩性。下一步将研究分析该算法中“拐点”出现的一般规律。